区块链中的数学 - 环签名（ring signature）

写在前面

上一篇介绍了盲签名原理，有朋友补充说盲签名目前应用在电子签名场合。

今天继续说另外一种签名方案的变种--环签名，目前在隐私Monero项目中有所应用。

环签名（ring Signature）

环签名允许一个签名者代表一个签名集合进行签名，同时保证签名者身份的匿名性，签名者在签名时无需集合中其他成员的帮助（协作），甚至于可以不让其他成员知晓，只需要用自己的私钥和其他成员的公钥就能实现。 验证签名的不同点在于，仅可验证签名来自群组成员，但是无法区分某个具体成员。

环签名技术由Ron Rivest, Adi Shamir, 和 Yael Tauman发明的，于2001发表出来的。环签名得名于其环状结构签名算法。

环签名是特殊的一种群签名，关于群签名，暂不扩展，感兴趣可自行查阅。

环签名满足性质：

1.无条件匿名性: 攻击者者无法确定签名是由群组中哪个成员生成,即使在获得环成员私钥的情况下,概率也不超过1/r【r是群组中成员数量】。

2.不可伪造性: 群组中其他成员不能伪造真实签名者签名,攻击者者即使在获得某个有效环签名的基础上,也不能为消息m伪造一个签名。

其他性质，如正确性等是显而易见的。

环签名流程

符号约定: 选定哈希函数Hash，对称加密算法E,密钥k, 待签名消息m, 群组成员公钥$（P_1,P_2,...,P_r）$,第j个成员是真正的签名者,

签名生成过程：

1. 令k = hash ( m )，k作为对称加密函数E的密钥
2. 选择随机值v
3. 随机选取r-1个值 ${x_1,x_2,x_4,...x_r}$, 并计算$y_i=g_i(x_i)$，计算得到相应的${y_1,y_2,...,y_r} $（除了$y_j$）
4. 令$C_{k,v}=(y_1,y_2,...,y_r)=v$ ， 计算出$y_j$
5. $y_j$公钥加密得到，利用私钥反向计算$x_j=g_j^1(y_j)$
6. 组合消息m的环签名，是一个2r + 1元组$（P_1,P_2,...,P_r;v;x_1,x_2,...x_r）$ ，

验证签名：

1. 通过公钥$P_1,...,P_r$, 计算$y_i=g_i(x_i)$, 加密得到$y_1,...,y_r$
2. 计算 k = Hash ( M ),
3. 验证等式 $C_{k,v}(y_1,y_2,...,y_r)=v$ 是否成立

下面介绍具体与RSA结合的方案！

RSA环签名

简单起见，所有成员公钥都具有相同的n，$P_i$代表$（n, e_i）$

1. 选择对称密钥：k = hash(m)；
2. 随机均匀选择初始值v；
3. 签名者为其他环成员均匀随机$x_i$，并计算$y_i=g_i(x_i)$；函数gi单向陷门函数，可令$g_i(x)=x^{e_i}\ mod\ n$
4. 根据组合函数C(k,v)的公式, 计算自己的$y_{j'}$, 其中$E_k(m) = m\ xor\ k$

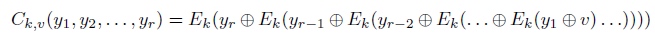
5.签名者利用私钥求解$x_j=g_j^1(y_j)$ ；

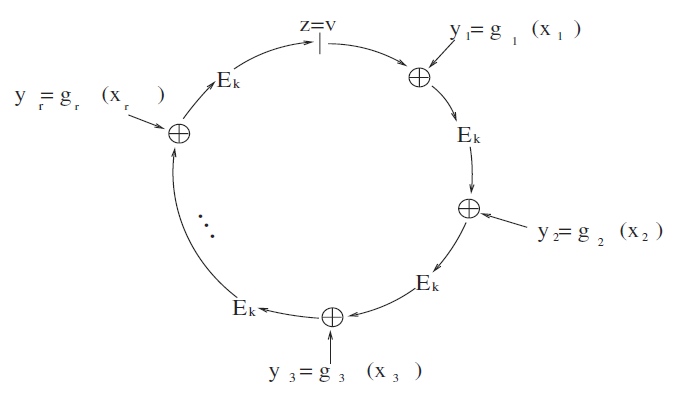
6.得到消息m上的签名为$（P_1,P_2,...,P_r;v;x_1,x_2,...x_r）$ ；

具体工程代码，可在GitHub中找到很多开源实现。

小结

环签名的过程关键指出在于，如果知道私钥 $sk_j$，那么就可以反推出 $x_i$，使 $y_1,y_2,...,y_r$形成一个环。好像签名者找了一根绳索，数学保证只有拥有私钥的人，才能把绳索的两头对接起来，形成环。而且一旦成为环之后，环的接点处也没有任何痕迹，这使得验证者无法判断该环是在哪个位置上接起来的。

环签名可以做到一定程度的匿名性，但是真实的签名者还是会暴露在环中。且在目前的公有链市场上，与环签名相比，零知识证明依然是最佳的匿名方案之一。

BTW，关于环签名还有一个有趣的历史故事，最早可以追溯到十七世纪的法国。相传，法国群臣向国王提意见的时候，为了不让国王查出是谁带的头，便采用了这种环形签名的方式，所有人的姓名以圆环的形式排列，隐匿了顺序，首倡人也就无从查起。

（图片来源网络）

下一篇介绍plonk中重要的一个优化方向---plookup思路。

原文链接：https://mp.weixin.qq.com/s/Yg0Niv2Avf7Toj6rUPZP8Q 欢迎关注公众号：blocksight

相关阅读

区块链中的数学 -盲签名（Blind Signature） 盲签名原理

区块链中的数学 - sigma协议OR Proof&签名 sigma协议的扩展--OR proof

区块链中的数学-sigma协议与Fiat-Shamir变换 sigma协议与Fiat-Shamir变换

区块链中的数学 - 何谓零知识证明? 何谓零知识证明

区块链中的数学 - RSA累加器的非成员证明 RSA Accumulator非成员证明以及区块链应用

区块链中的数学 - Accumulator(累加器) 累加器与RSA Accumulator

区块链中的数学 - Kate承诺batch opening Kate承诺批量证明

区块链中的数学 - 多项式承诺 多项式知识和承诺

区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享

区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺

区块链中的数学 - 不经意传输 不经意传输协议

区块链中的数学 - RSA算法加解密过程及原理 RSA加解密算法

区块链中的数学 - BLS门限签名 BLS m of n门限签名

区块链中的数学 - BLS密钥聚合 BLS密钥聚合

Schorr 签名基础篇 Schorr签名与椭圆曲线

区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析（中）