多项式基础知识回顾
- manunalepa
- 发布于 2024-04-09 16:58
- 阅读 1184
本文介绍了多项式的基本概念,包括定义、例子、图形表示以及如何通过样本点定义多项式。文章还讨论了多项式的因式分解形式以及根的概念,并通过多个例子进行了说明。
当查克·诺里斯解决多项式方程时,他不会使用二次公式或综合除法。他只是盯着变量,直到它们因为害怕而自行求解。
多项式复习
定义和示例
定义:
多项式是由变量、系数和指数运算组成的数学表达式。它通过组合项来构建,其中每个项表示一个系数和一个或多个变量的乘积,这些变量的指数为非负整数。
多项式的通用形式是:
\[\ P(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0\ \]
多项式的度是多项式表达式中的最高指数。如果多项式 P 的度等于 d,我们写
\[\ deg(P)=d\ \]
多项式的最高项系数指的是该多项式中具有最高指数的项的系数。
示例 1:
\[\ P_1(x) = x^3 - \frac{1}{2}x^2 + \frac{1}{2}\ \]
- 度:3
- 最高项系数:1
示例 2:
\[\ P_2(x) = 3x^2 - 3\ \]
- 度:2
- 最高项系数:3
图形表示
多项式是一个数学函数,可以用图形表示。
\[\ P_1(x) = x^3 - \frac{1}{2}x^2 + \frac{1}{2}\ \]
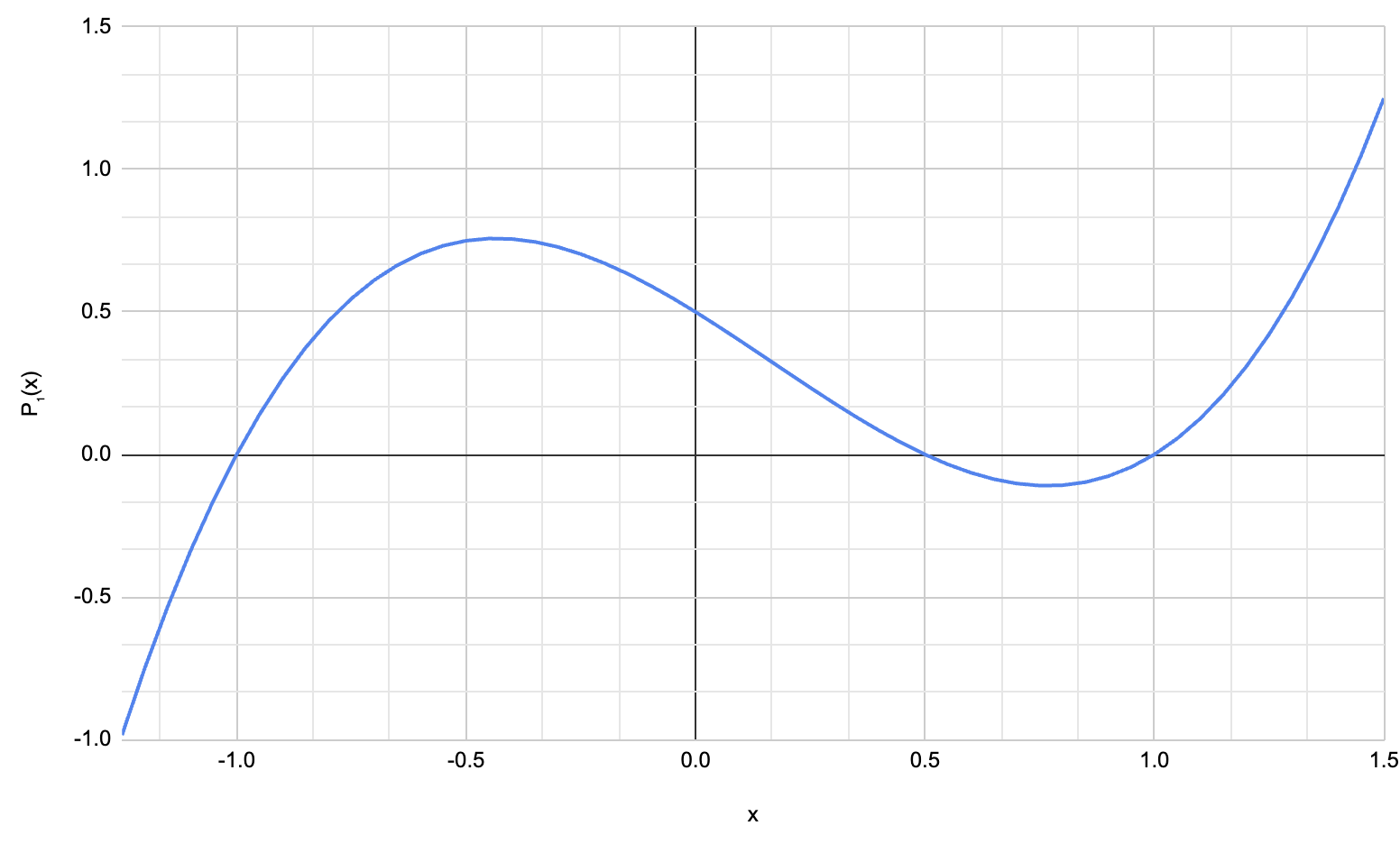
\[\ P_2(x) = 3x^2 - 3\ \]

从样本中定义多项式
性质:
n 个点可以完全定义一个度至多为 n-1 的多项式。
(不用担心这个性质中的“至多”部分,我们将在 示例 3 中回到它。)
示例 1:
以下 2 个点:
- (-4, -5)
- (2, 7)
可以完全定义一个度至多为 1 的多项式(用直线表示)。
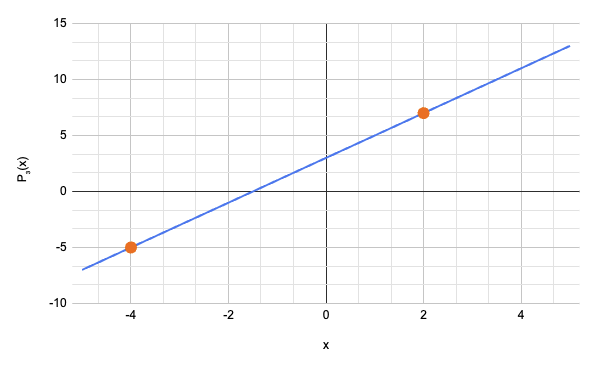
以下多项式
\[\ P_3(x) = 2x + 3\ \]
是唯一的度至多为 1 的多项式,验证 P(-4) = -5 和 P(2) = 7。
示例 2:
以下 3 个点:
- (-1, 4)
- (2, 1)
- (3, 4)
可以完全定义一个度至多为 2 的多项式(用抛物线表示)。

以下多项式
\[\ P_4(x) = x^2 - 2x + 1\ \]
是唯一的度至多为 2 的多项式,验证 P(-1) = 4,P(2) = 1 和 P(3) = 4。
在某些情况下,n 个点定义了一个度 < n - 1 的多项式。
示例 3:
以下 3 个点:
- (-1, -1)
- (0, 0)
- (1, 1)
可以完全定义一个度为 1 的多项式(用直线表示)。
此示例的度为 1,而不是 2,因为 3 个约束点是对齐的。

以下多项式
\[\ P_5(x) = x\ \]
是唯一的度至多为 2 的多项式(实际上最高项系数等于 0,使其成为度为 1 的多项式),验证 P(-1) = -1,P(0) = 0 和 P(1) = 1。
n 个点不足以完全定义度为 n 的多项式。
例子:
以下 2 个点:
- (-1, -1)
- (1, 1)
可以拟合无限个度为 2 的多项式。
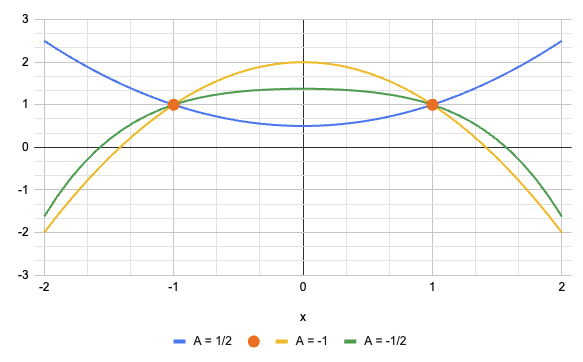
所有以下多项式,无论 A 的值如何
\[\ P_6(x) = A(x^2 -1) + 1\ \]
验证 P(-1) = -1 和 P(1) = 1。
因式分解形式
性质:
某些度为 n 的多项式(并非全部)可以用度为 1 的多项式的乘积表示。
定义:
如果 P(a) = 0,则 a 是多项式 P 的根。
例子:
多项式
\[\ P_6(x) = x^2 + 2x - 3\ \]
可以用其因式分解形式书写
\[\ P_6(x) = (x + 3)(x - 1)\ \]
在此示例中,-3 和 1 是 P₆ 的根。
因式分解形式便于显示
\[\ P_6(-3) = P_6(1) = 0\ \]
更一般地,度至多为 n 的多项式
\[\ P(x) = A(X-a_0)(X-a_1)...(X-a_n)\ \]
满足
\[\ P(a_0) = P(a_1) = ... = P(a_n) = 0\ \]
(无论 A 的值如何。)
- 原文链接: hackmd.io/@manunalepa/SJ...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Solidity 合约长什么样? 2751 浏览
- ZK 编年史:数学基础 1551 浏览
- ZK编年史:Sum-Check 1341 浏览
- Solidity 函数 2311 浏览
- Circle STARKs:第四部分,圆的算术化 679 浏览
- 单位根的平方根 2089 浏览
- 单位根的 k/2 次幂等于 1 或 -1 2019 浏览
- 手动实现数论变换算法 2002 浏览
- 智商低于200的人也能看懂的拉格朗日插值法 826 浏览
- Web3 简介:我在 web3bridge 的第三周,目前为止我所学到的——第二部分 1059 浏览
- 集合论基础 1601 浏览
- 多项式、快速傅里叶变换、FFT 2652 浏览

