密码学基础：算术电路

这是一系列关于加密技术的文章中的一部分。如果这是你遇到的第一篇文章，我强烈建议你从系列的开始阅读。

上次，我们深入探讨了一个 零知识证明 协议的特定示例。尽管优化和性能问题不谈，它涵盖了所需的用例：证明一个数字在 某个范围 内。然而，该协议是 极其具体 的，为了另一个声明而制作另一种协议需要专门的研究，可能会导致一整个不同的步骤序列。

我们总结时提到，零知识证明 的 通用框架 可能是一个有趣的追求目标。

而我们将会到达那个目标——只是现在还不是时候！

今天的计划是展示一些 基础，我们将在下篇文章中 立即 以此为基础进行构建。

既然我们在上次讨论中提到了 比特，那么我们就稍微绕一下，简要复习一下它们的用途。可以吗？

二进制电路

如果你正在阅读这篇文章，很可能你对计算机至少是 有点 兴趣，所以我们来谈谈这个话题。

比特作为计算机科学中的数据表示基本单位的事实，与计算机的工作原理密切相关。简单地说，流过电路的 电流 可以被视为 一 (1)，而在同一电路中 没有电流 流动的状态可能表示为 零 (0)。确实，这些电流就是 比特 在物理世界中的表现方式。

但是，如果我们不能对这些数据执行某些 操作，计算机就不会如此酷炫。

我们可以做的第一件事情就是以各种方式 组合 两个比特（记住，它们只是 电信号）。例如，我们可以创建一个 盒子，只有在两个信号输入也都是 1 时才输出 1，否则输出 0：

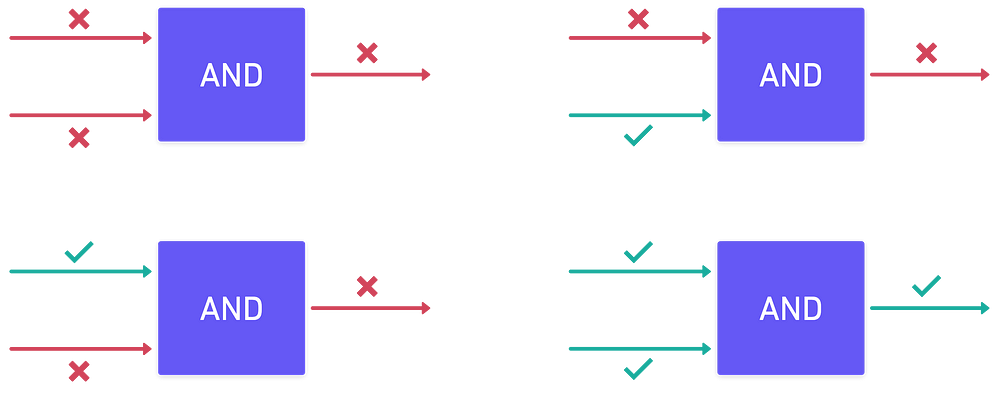
AND 门的运作

这些类型的盒子称为 逻辑门，它们使计算机能够进行魔法。其他 简单 门的存在，例如 NOT、OR、XOR、NAND、NOR 和 XNOR——它们都是电路的巧妙排列。

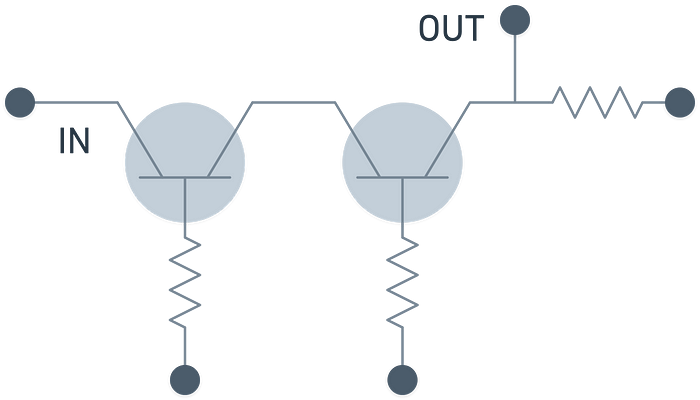
一个 AND 门的实际电路大致看起来是这样的

两个信号仍然太少——我们可以做得更好。所以，我们可以通过排列一些门来处理多个输入，在这个过程中获得一系列输出。门的排列方式称为 电路，它本质上是一个 计算模型。

例如，我们可以用这个相对简单的电路来加两个 两比特数字 A =(a ₀, a₁) 和 B =(b ₀, b₁)：

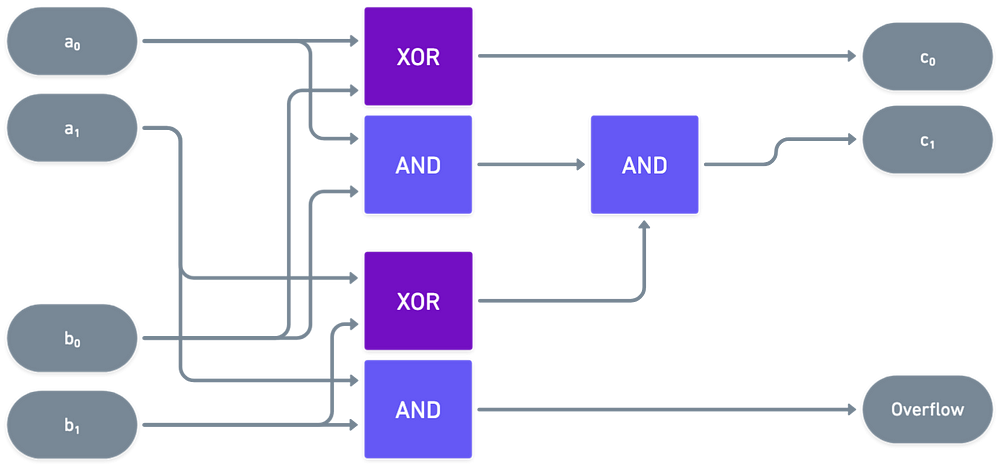
结果可能是 3 比特长——这对应于第三个输出，溢出

可以通过使用多个门和处理多个输入来创建各种用途的电路。

改变视角

让我们通过另一种视角来看待这些二进制电路。比特 只是一个属于集合 {0,1} 的数字。这个集合也双重成为一个 有限域：加法、乘法、减法和除法（除了 0 以外的一切）都被定义。我们使用 模 运算来保持在范围内——例如， 1 + 1 mod 2 = 0。

在这个意义上，我们可以将门视为对该有限域上进行的 数学运算。XOR 门正确地表示 模 2 加法，而 AND 门表示 模 2 乘法：

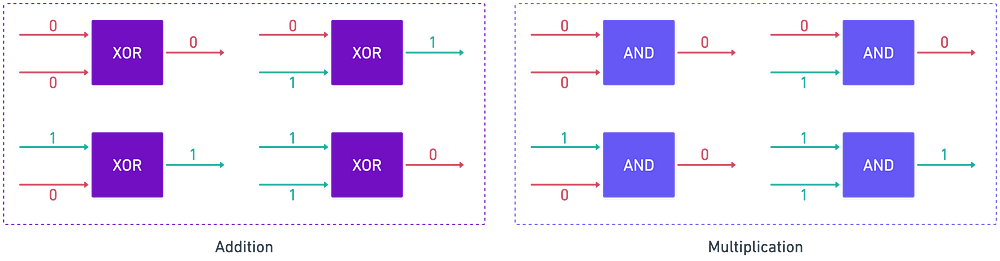
好吧，酷……接下来呢？

假设我们将输入标记为 x 和 y。我们再加一个 1 作为输入，以作补充。如果我们设置一些门，会发生什么？

![](https://img.learnblockchain.cn/2025/02/1...