利用 WebGPU 加速 ZK 证明:技术与挑战 - ZKSECURITY
- zksecurity
- 发布于 2025-04-26 20:38
- 阅读 1548
本文探讨了利用 WebGPU 加速客户端零知识证明(ZKP)的方法。WebGPU 是一种可以在多种平台(包括移动设备)上利用 GPU 的技术,通过并行计算和优化内存使用,能够显著提升证明速度。文章详细介绍了 WebGPU 的基本原理、内存层级结构,以及在 WGSL 中实现 NTT(数论变换)的优化过程,最后讨论了将 WebGPU 集成到 ZK 框架中的挑战和未来方向。

客户端证明对于实现保护隐私的 ZK 应用至关重要,但仍存在两个主要瓶颈:时间和空间(内存限制)。 有许多技术突破解决了这些限制,例如:
- 增量可验证计算(IVC)技术
- 委托证明生成
- 将完整证明委托给可信执行环境(TEE)
- 通过 coSNARKs 进行完整证明委托(例如 zkSaaS)
- 通过将电路分为私有计算和公共计算来进行部分证明委托(Aztec 的 zk-rollup)
- 流式传输 witness ( Gemini, Ligetron)
另一种方法是利用 GPU,它可以显著提高可并行任务的性能。 Ingonyama 的 ICICLE 是一个用于 ZKP 的 CUDA 库,是这种方法的主要例子,并且已集成到各种 ZK 框架中。 但是,基于 CUDA 的解决方案无法在大多数移动 GPU 上运行。
WebGPU 是用于在移动设备上利用 GPU 的更突出的框架之一,它是一个强大的抽象,可与 Android 和 iOS 上的 GPU 以及大多数其他平台(Linux、Windows、MacOS 等)一起使用。 顾名思义,它默认适用于主流浏览器(Chrome、Edge、Brave,Safari 在 iOS 18.2 中启用了它),Firefox 将很快启用它),并且它也可以与原生 iOS 和 Android 应用程序集成。
最近,我们将 WebGPU 与 Starkware 的 Stwo 证明器集成,并发现了 评估约束多项式的 5 倍改进和整个证明流程的 2 倍改进。 在这篇文章中,我们想分享我们一路走来的一些经验,并希望说服读者将其集成到他们的证明器框架中。
WebGPU 基础知识:计算工作流程和内存层次结构
在深入研究具体的实现和优化之前,让我们先温和地介绍一些 GPU 的基本概念。 使用 GPU 的程序的简化工作流程如下所示:
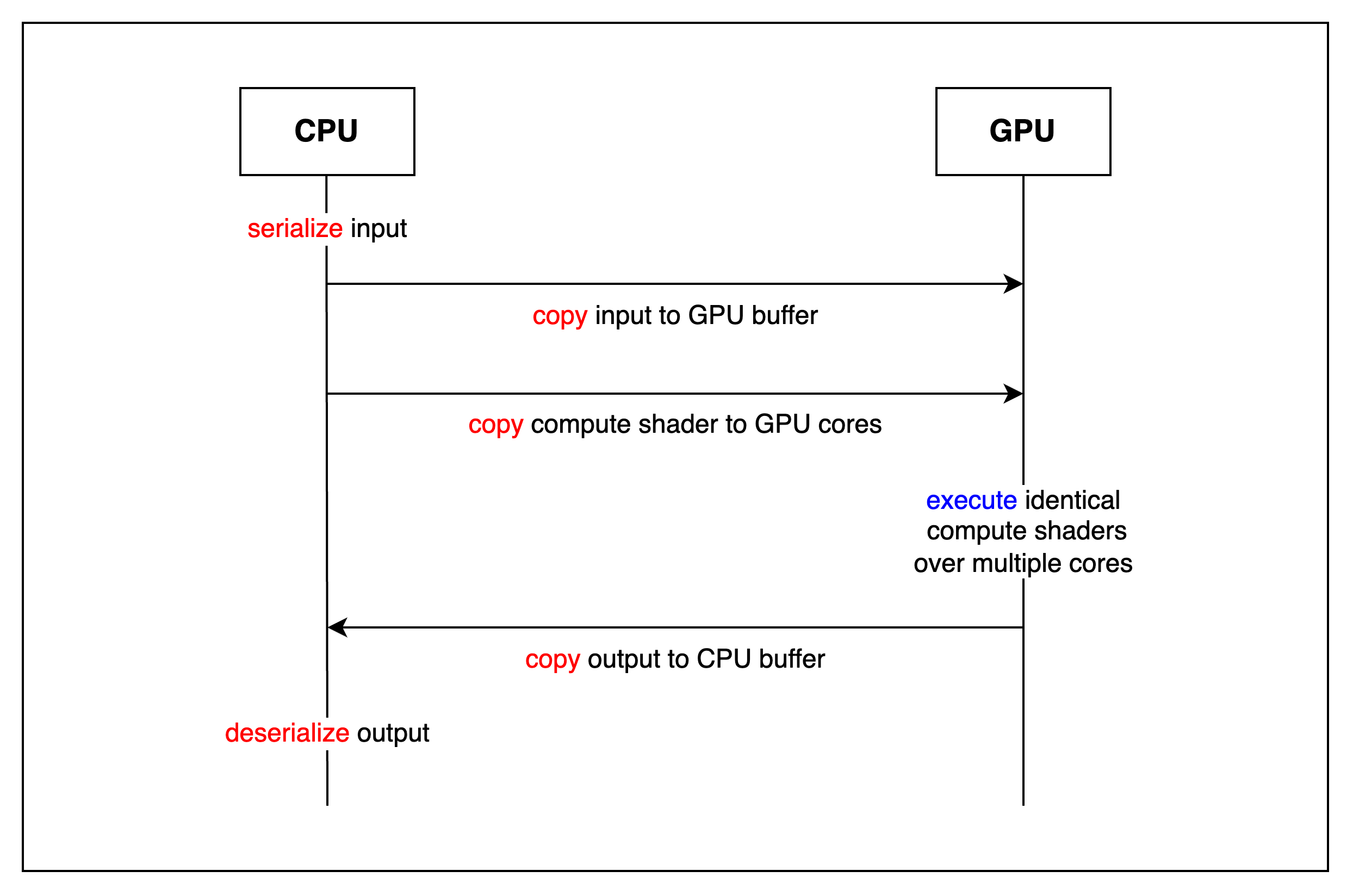
简而言之,CPU 向 GPU 提供一个程序(称为计算着色器)以及一些输入。 GPU 将该程序复制到其多个内核中的每一个内核,并且每个内核并行执行该程序。 所有内核完成执行程序后,GPU 将结果返回给 CPU。 正如红色字体所暗示的那样,除了在 GPU 上执行之外,还有许多其他操作,我们稍后将展示它们是将计算卸载到 GPU 的主要瓶颈之一。
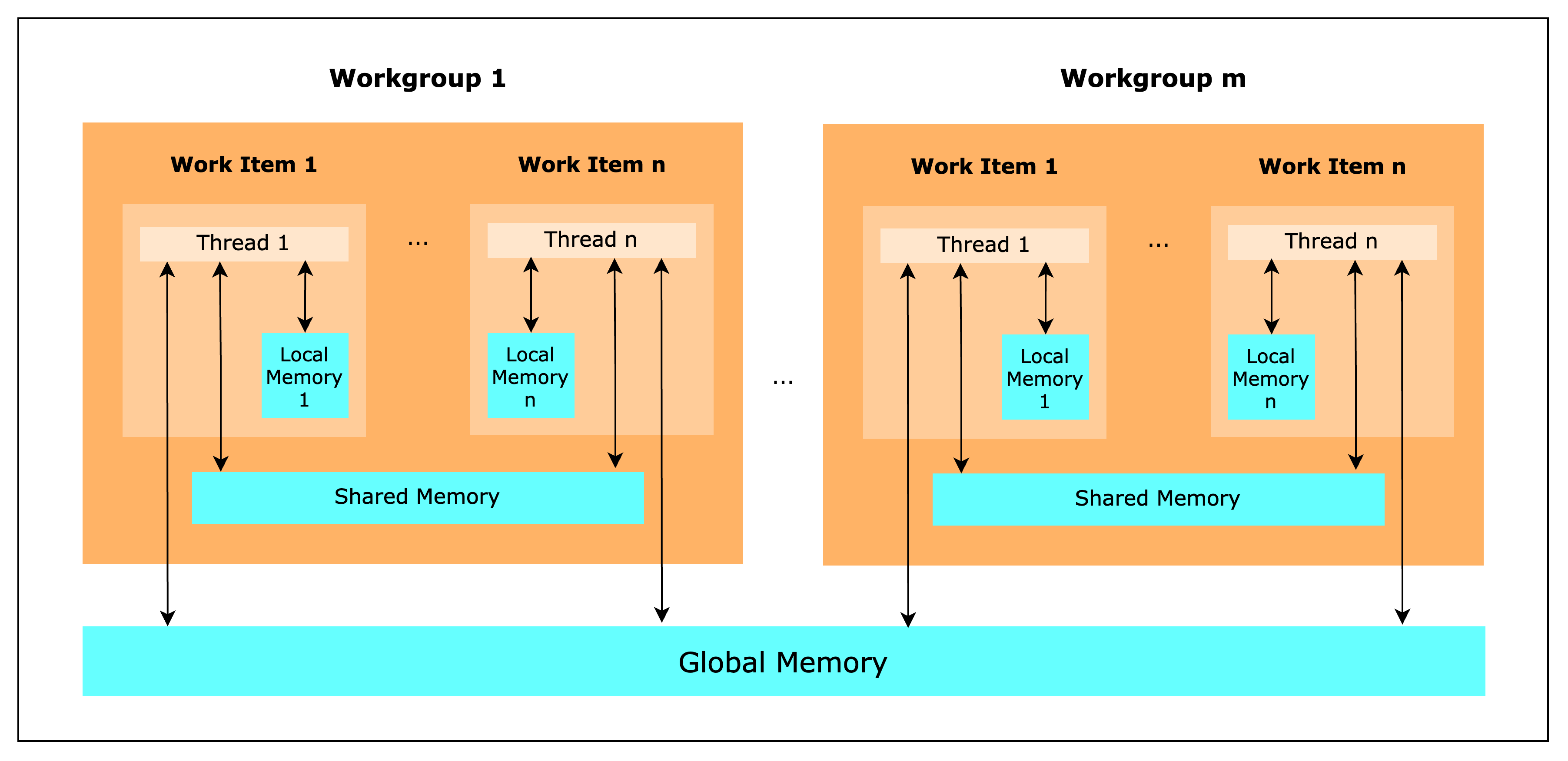
另一个需要理解的概念是 GPU 的内存层次结构。 特定术语在不同的 GPU 供应商之间有所不同,但专注于 WebGPU 中使用的术语,GPU 基本上由多个 workgroups 组成,每个 workgroups 又由多个 work items 组成。 每个 work item 都有一个 thread,可以访问自己的 local memory,由于它最接近线程,因此访问速度非常快(可以认为是 1 个周期)。 但是 work item 也可以访问 shared memory,同一 workgroup 中的任何 work items 都可以访问它。 它旨在充当同一 workgroup 线程之间的缓存,并由于其与线程的物理接近性而提供低延迟的内存访问。 最后,任何 workgroup 的所有 work items 都可以访问 global memory,由于它位于 VRAM 中,因此访问速度最慢,因此需要最多的周期。 一般来说,对 global memory 的访问也不会被缓存,这意味着每次调用 global memory 时,GPU 都需要从 VRAM 中检索数据。 一个值得注意的例外是当在 global memory 上实例化一个只读缓冲区时,该缓冲区将被 GPU 缓存,因此访问速度会更快。
简而言之,GPU 可以访问内存层次结构中的 3 个不同级别,并且还支持缓存。 下表显示了编写 WGSL(WebGPU 的着色器语言)时可以使用的每个级别的变量类型。
| 变量类型 | 层次结构 | 大小 | 访问 | 速度(周期是估计值) |
|---|---|---|---|---|
var<private> |
Work Item | 每个线程的寄存器/内存 | 读写 | 最快 (~1 cycle) |
var<workgroup> |
Workgroup | ~16KB | 读写 | 快 (~5-20 cycles) |
var<uniform> |
全局 | ~64KB | 只读 | 中等(已缓存,~20-100 cycles) |
var<storage> |
全局 | 128MB~(取决于 VRAM 大小) | 读写 | 最慢(未缓存,~200-800 cycles) |
有关 WebGPU 的更详细说明,我们建议阅读这篇文章:WebGPU-All of the cores, none of the canvas。
现在,鉴于我们现在对 GPU 的工作原理有了一些了解,让我们通过逐步优化 FFT 操作来深入了解如何使用 WebGPU 中的工具。
在 WebGPU 中实现 NTT(数论变换)的注意事项
数论变换(NTT)本质上是在有限域而不是复数上执行的快速傅里叶变换(FFT)。 在 zk 证明协议中,需要对多项式进行各种运算,NTT 可用于插值或评估这些多项式。
在本节中,我们将从头开始在 WGSL 中构建一个 NTT。 我们将从一个基本的单线程版本开始,然后逐步添加多线程和 workgroup 内存优化。 WebGPU 计算着色器允许你利用 GPU 的并行能力来执行 NTT 等任务。 每个步骤都包括清晰的 WGSL 代码片段和解释。
Rust 实现
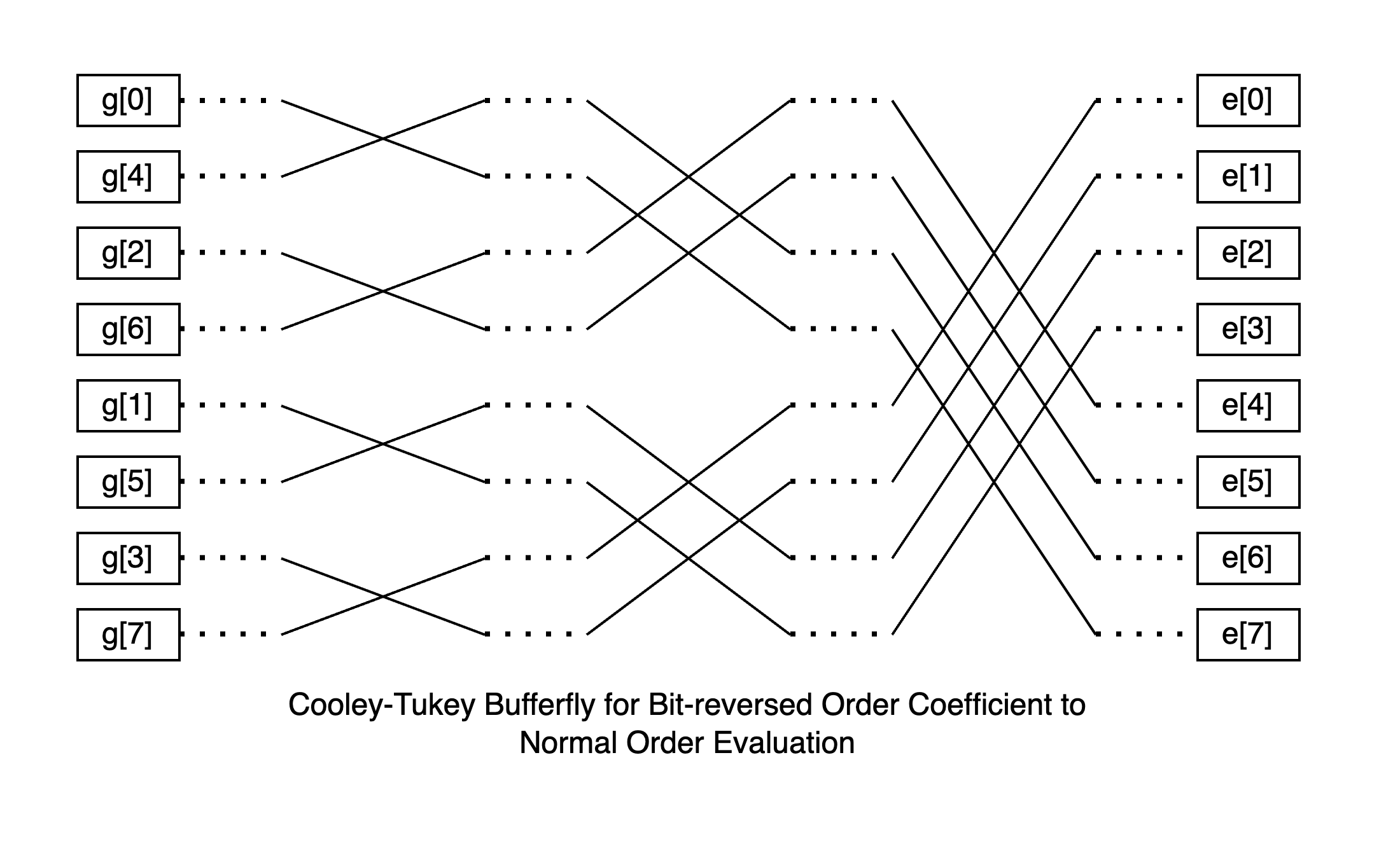
此 Rust 实现使用 Cooley-Tukey 算法。 它将 NTT 分解为连续的阶段,每个阶段应用蝶形运算来组合元素,从而有效地就地转换数据。 有关更多详细信息,请查看 关于 Cooley-Tukey FFT 算法的 Wikipedia 文章。 由于 NTT 是在有限域上定义的 FFT,因此 NTT 和 FFT 背后的原理是相同的。
fn ntt(data: &mut [u32], twiddles: &[u32]) {
let n = data.len();
let mut stride = 1;
let mut twiddle_offset = 0;
while stride < n {
let half_jump = stride;
let jump = stride * 2;
for base in (0..n).step_by(jump) {
for j in 0..half_jump {
let even_index = base + j;
let odd_index = even_index + half_jump;
let a = data[even_index];
let b = data[odd_index];
let tw = twiddles[twiddle_offset + j];
let res = butterfly(a, b, tw);
data[even_index] = res.even;
data[odd_index] = res.odd;
}
}
twiddle_offset += half_jump;
stride *= 2;
}
}
单线程 WGSL 实现
这是我们 NTT 实现的最简单版本。 它旨在在单个 GPU 线程上运行,这意味着所有蝶形运算都按顺序执行。 多项式的系数在程序开始之前加载到 data storage 变量中。 它们是就地计算的,因此多项式的评估结果也存储到 data storage 变量中。 执行结束后,必须将此值检索到 CPU 内存。
尽管底层逻辑是相同的,但此单线程 WGSL 实现的执行速度比单线程 Rust 版本慢。 即使不考虑 CPU 到 GPU 缓冲区的开销以及调用 GPU 时产生的延迟也是如此。
这是因为 GPU 经过优化,可以并发执行许多简单的操作,与现代 CPU 中通常发现的几十个执行单元相比,它可以拥有数千个执行单元。 但是,单个 GPU 执行单元的性能较差,这最终导致此实现的整体性能较慢。 此外,虽然 CPU 使用统一的内存系统运行,但 GPU 具有多层内存层次结构。 在这种情况下,data storage 变量上的就地计算是在全局内存中进行的,这是 GPU 中最慢的内存类型,进一步影响了性能。
@group(0) @binding(0)
var<storage, read_write> data: array<u32>;
@group(0) @binding(1)
var<storage, read> twiddles: array<u32>;
const N: u32 = 8u; // NTT size
@compute @workgroup_size(1, 1, 1)
fn single_thread_ntt(@builtin(local_invocation_id) local_id : vec3<u32>) {
var stride: u32 = 1u;
var twiddleOffset: u32 = 0u;
while (stride < N) {
let halfJump: u32 = stride;
let jump: u32 = stride * 2u;
for (var base: u32 = 0u; base < N; base = base + jump) {
for (var j: u32 = 0u; j < halfJump; j = j + 1u) {
butterfly(base, j, halfJump, twiddleOffset);
}
}
// Update the twiddle offset and stride
twiddleOffset = twiddleOffset + halfJump;
stride = stride * 2u;
// No need to synchronize since it's running on a single thread
}
}
多线程版本
一个 workgroup 是线程的一个小集合。 在 WebGPU 中,并行化由 workgroup 的大小和执行的 workgroup 数量决定。 例如,如果你使用如下所述的 dispatch_workgroup 运行大小为 64 的 workgroup,则将产生 64 * 12 = 768 个线程。
compute_pass.dispatch_workgroups(3, 2, 2); // e.g., spawn 3 * 2 * 2 = 12 workgroups
以下示例演示了使用单个 workgroup 并行化任务。 有 4 个线程,并且在 NTT 的每个 stride 迭代中,线程将索引分配给它们自己进行处理,之后进行同步,然后重复此过程。 在此代码中,我们调用 storageBarrier() 以同步单个 workgroup 中调用之间对 storage 地址空间中的缓冲区的访问。
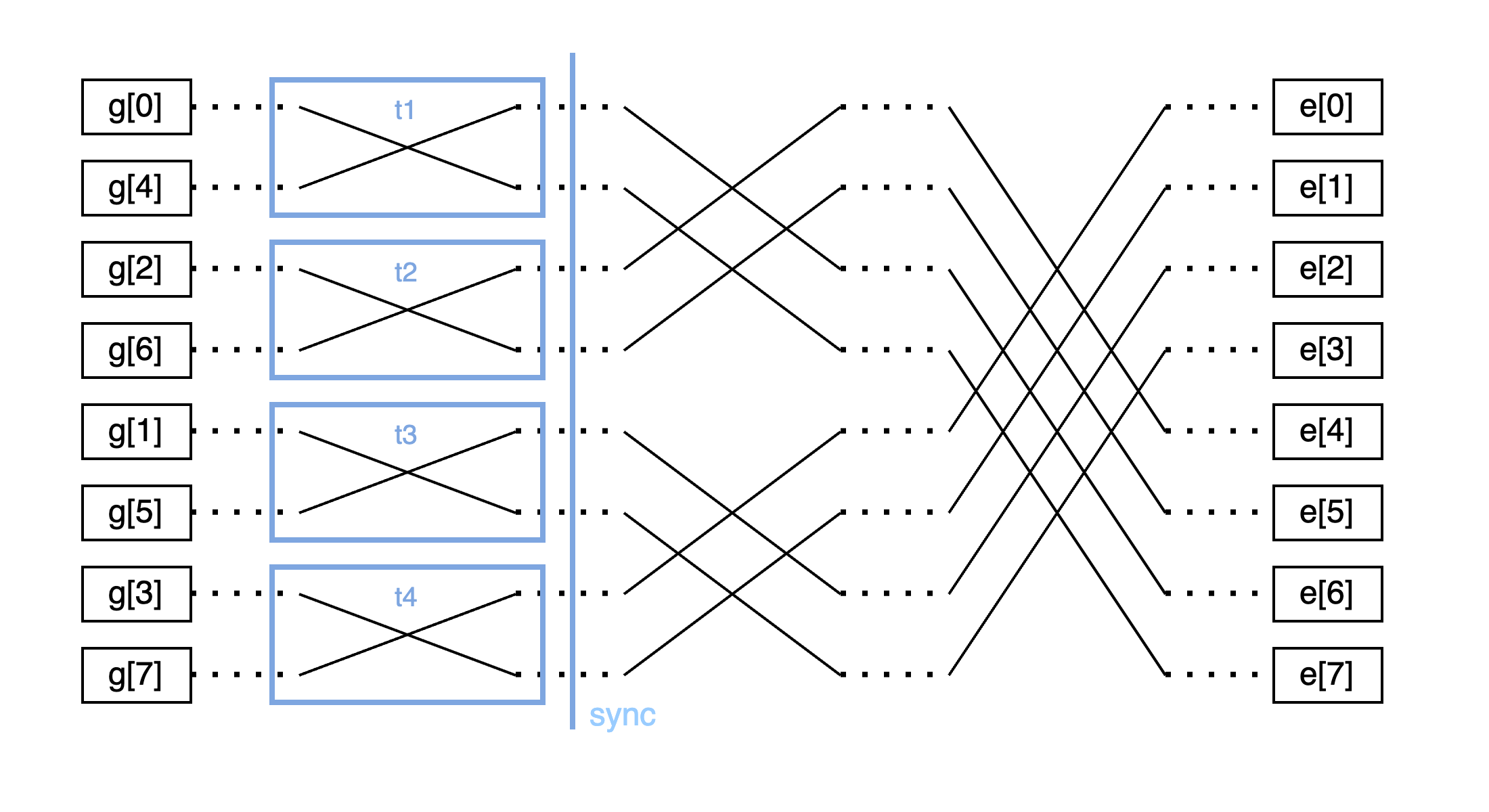
此示例的优点是使用多个线程; 但是,它每次都需要访问 data storage 变量(同样,storage 变量 - 全局内存 - 是 GPU 中最慢的内存类型),并且需要所有线程在每个 stride 上同步,从而为进一步优化留下了空间。
const NUM_THREADS: u32 = 4u;
// 1 Workgroup, 4 threads per workgroup, 4 threads total
@compute @workgroup_size(NUM_THREADS, 1, 1)
fn single_workgroup_ntt(@builtin(local_invocation_id) local_id: vec3<u32>) {
var stride: u32 = 1u;
var twiddleOffset: u32 = 0u;
while (stride < N) {
let halfJump: u32 = stride;
let jump: u32 = stride * 2u;
// Total number of base iterations (each iteration increments by jump)
let numBases: u32 = N / jump;
let threadId: u32 = local_id.x; // 0 ~ (NUM_THREADS-1)
// Each thread starts at its index and processes every 4th iteration
for (var i: u32 = threadId; i < numBases; i = i + NUM_THREADS) {
let base: u32 = i * jump;
for (var j: u32 = 0u; j < halfJump; j = j + 1u) {
butterfly(base, j, halfJump, twiddleOffset);
}
}
// Update the twiddle offset and stride
twiddleOffset = twiddleOffset + halfJump;
stride = stride * 2u;
// Use storageBarrier() to synchronize threads for
// correct access to the 'data' storage variable.
storageBarrier();
}
}
使用多个 workgroup
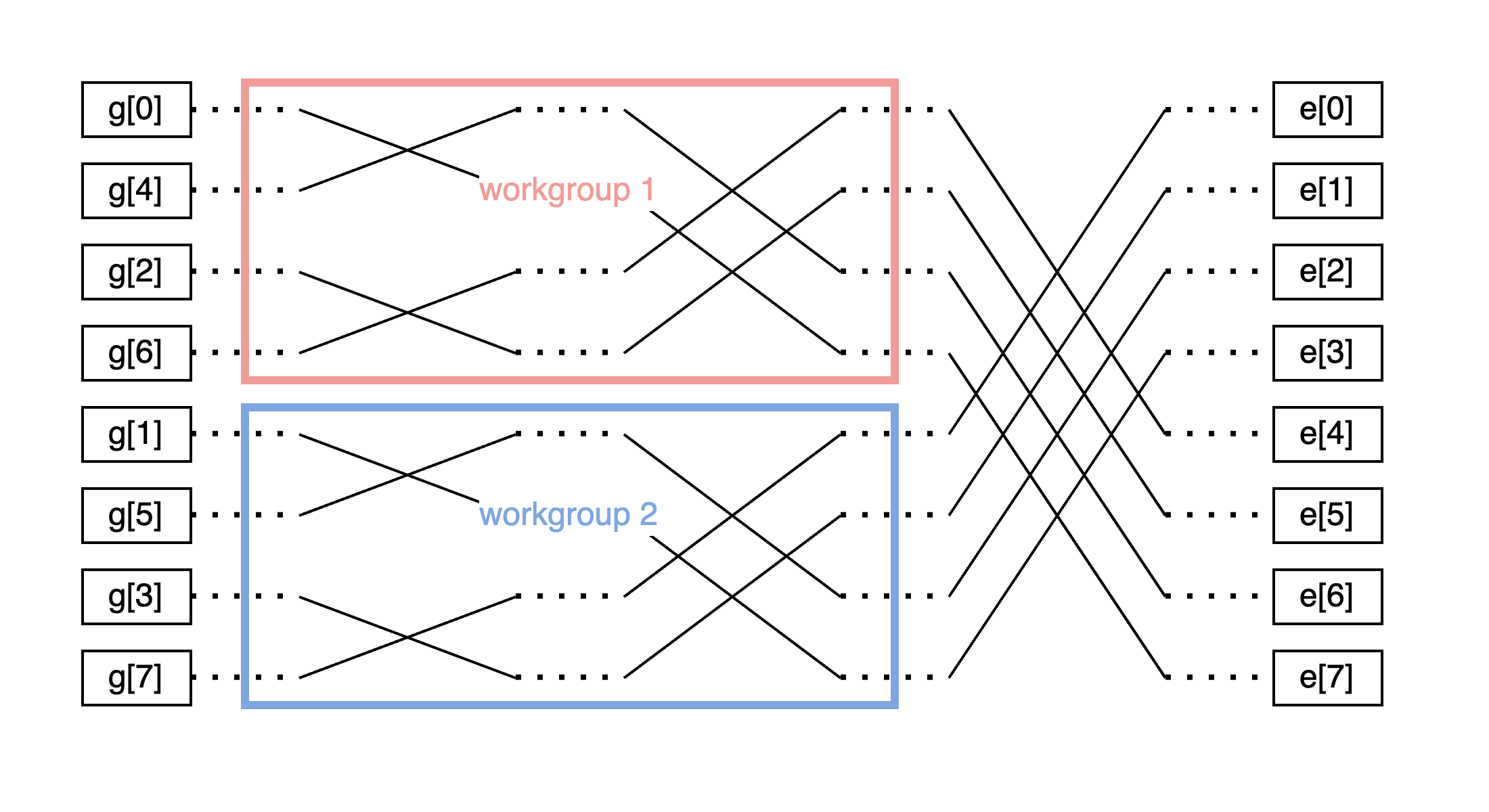
在 CT 算法中,由于可以在一定程度上独立执行计算,因此可以隔离它们并在每个 workgroup 中执行。 这种方法允许使用访问速度比 storage 变量更快的 workgroup 内存。 此外,此实现不需要所有线程在每个 stride 上同步,这是一个很好的改进。 在此代码中,我们调用 workgroupBarrier() 以同步单个 workgroup 中调用之间对 workgroup 地址空间中的缓冲区的访问。
所以这段代码如下所示:
- 每个 workgroup 仅对其自身分配的范围(
baseIndex到baseIndex + subBlockSize - 1)执行 NTT 蝶形运算。 - 在重复
partialStages次之后,它就完成了。 - 一旦前 log2(subBlockSize) 个阶段完成,我们需要开始合并成对的子块(形成更大的子块)。
此时,不同的 workgroup 可能会访问相同的内存范围,因此需要跨 workgroup 同步。
标准 WGSL 不提供全局屏障(即,没有内置方法来跨不同的 workgroup 进行同步)。 因此,我们通常会结束调度 → 让 CPU(主机)同步所有内容 → 然后启动另一个调度来处理剩余的阶段。
// launch multi_workgroup_ntt() using 2 workgroups
compute_pass.set_pipeline(&self.multi_workgroup_ntt);
compute_pass.dispatch_workgroups(2, 1, 1);
// let cpu synchronize everything, then launch another dispatch
compute_pass.set_pipeline(&self.single_workgroup_ntt);
compute_pass.dispatch_workgroups(1, 1, 1);
const N: u32 = 8u;
const NUM_THREADS: u32 = 4u;
var<workgroup> workgroup_data: array<u32, N>;
// External assumption: for instance, if we dispatch 2 workgroups,
// => totalWorkgroups = 2
// => subBlockSize = N / totalWorkgroups = 4
// => partialStages = log2(4) = 2 (meaning we can proceed up to 2 stages without cross-workgroup conflicts)
// Because the input is in bit-reversed order, each "4-sized section" will not conflict with others
// for the first 2 stages. After that, sub-blocks must merge, requiring global sync.
@compute @workgroup_size(NUM_THREADS, 1, 1)
fn multi_workgroup_ntt(
@builtin(local_invocation_id) local_id: vec3<u32>,
@builtin(workgroup_id) workgroup_id: vec3<u32>,
// How many workgroups to use (e.g., 2)
totalWorkgroups: u32,
// The "maximum number of stages" to be processed in this dispatch (e.g., 2)
partialStages: u32,
) {
// =====================================================================
// Here, it is assumed that there is code to copy data from storage memory (data)
// to workgroup memory (workgroup_data) at the beginning.
// =====================================================================
// Current workgroup ID
let gId = workgroup_id.x; // 0 ~ (totalWorkgroups-1)
// Thread ID within a single workgroup
let tId = local_id.x; // 0 ~ (NUM_THREADS-1)
// subBlockSize: The size of the physical section this workgroup will handle
let subBlockSize = N / totalWorkgroups;
// baseIndex: The start index in memory for this workgroup
let baseIndex = gId * subBlockSize;
var stage: u32 = 0u;
var stride: u32 = 1u;
var twiddleOffset: u32 = 0u;
// Repeat partialStages times (e.g., 2 times)
while (stage < partialStages) {
let halfJump = stride;
let jump = stride * 2u;
// Traverse base in increments of 'jump' only within this sub-block
let numBasesInSubBlock = subBlockSize / jump;
// Parallel processing: the NUM_THREADS in one workgroup split up the base loop
var i = tId;
while (i < numBasesInSubBlock) {
let base = baseIndex + i * jump;
for (var j: u32 = 0u; j < halfJump; j = j + 1u) {
butterfly_workgroup(base, j, halfJump, twiddleOffset);
}
i = i + NUM_THREADS;
}
twiddleOffset = twiddleOffset + halfJump;
stride = stride * 2u;
stage = stage + 1u;
// Use workgroupBarrier() to synchronize threads for
// correct access to the 'workgroup_data' workgroup variable.
workgroupBarrier();
}
// =====================================================================
// Here, it is assumed that there is code to copy the computed results
// from workgroup memory (workgroup_data) back to storage memory (data).
// =====================================================================
// By this point:
// - Each workgroup has finished partialStages (=2) stages of NTT on its own subBlockSize section
// - There was no conflict between different workgroups (thanks to the bit-reversed ordering).
//
// The remaining stages (log2(N) - partialStages) involve merging sub-blocks,
// which is not safe to do in a single dispatch without cross-workgroup sync.
// Typically, the CPU will issue another dispatch to finish the remaining stages.
}
更多需要考虑的事项
workgroup 大小和整体性能之间的权衡
workgroup 的大小对于充分利用 GPU 的并行处理能力至关重要。 如果 workgroup 太小,硬件的并行执行单元将无法得到充分利用,从而导致性能欠佳。 相反,过大的 workgroup 可能会过度消耗寄存器和共享内存等资源,从而减少可以同时执行的 workgroup 数量。 作为一般准则,建议从 64 个线程开始,或者从与底层硬件的 warp/wavefront 大小相匹配的倍数开始。 此策略旨在与 GPU 的 warp(或 wavefront)大小(例如,NVIDIA 使用 32 个,AMD 使用 64 个)对齐,以最大程度地实现并行性。
尽量减少 CPU 和 GPU 之间的数据传输
分析你的 WebGPU 代码通常会发现,在 CPU 和 GPU 之间复制缓冲区(双向)可能是一个主要的性能瓶颈。 这些数据传输的开销会很快超过其他优化,从而抵消潜在的收益。 作为一种实用的方法,通常更有效的方法是减少交换的数据量,并增加 GPU 上的计算工作负载。 通过重构你的算法以在 GPU 上执行尽可能多的处理,你可以最大程度地减少这些昂贵的传输并获得显着的性能提升。
使用 WebGPU 的挑战
着色器语言约束
现在我们已经熟悉了如何使用 WGSL 编写代码以获得最佳性能,让我们通过将其与其他流行的着色器语言进行比较来探索其一些局限性:
| 特性 | WGSL (WebGPU) | CUDA (NVIDIA) | MSL (Apple Metal) | HLSL (DirectX) | GLSL (OpenGL/Vulkan) |
|---|---|---|---|---|---|
| 标量类型 | ✅ f32, i32, u32, bool (❌ 没有 f64/i64) |
✅ f16, f32, f64, i8, i16, i32, i64, u8, u16, u32, u64, bool |
✅ f16, f32, i8, i16, i32, i64, u8, u16, u32, u64, bool |
✅ f16, f32, f64, i8, i16, i32, i64, u8, u16, u32, u64, bool |
✅ f16, f32, f64, i8, i16, i32, i64, u8, u16, u32, u64, bool |
| 任意长度数组 | ❌ 仅允许用于 storage 内存空间 | ✅ (通过 malloc, new, vector<T>) |
✅ (通过 device array<T>) |
✅ | ❌ (仅允许用于具有缓冲区存储的 Vulkan GLSL) |
| 隐式标量转换 | ❌(需要显式转换) | ✅(例如,int → float) |
✅ | ✅ | ✅ |
| 递归 | ❌ | ✅ | ❌ | ✅ | ❌ (仅允许用于使用某些扩展的 Vulkan GLSL) |
| 函数重载 | ❌ | ✅ | ✅ | ✅ | ✅ |
| 循环依赖 | ❌ | ✅ | ✅ | ✅ | ✅ |
一些亮点:
- WGSL 本身不支持 64 位整数,因此任何超过 32 位的整数都需要分解。
- 对任意长度数组的支持非常有限:只能将运行时大小的数组创建为 storage 内存空间缓冲区(即全局内存空间)的最后一个元素。
有限的库生态系统
另一个挑战是与 CUDA 等现有语言相比,缺少库,在 CUDA 中,有通用 GPU 计算的优化实现(cuDNN、cuFFT、cuBLAS 等)。 此外,没有对文件导入的本机支持,这意味着要使用着色器库,开发人员需要手动连接着色器代码,从而增加了函数重载和循环依赖等错误的风险。
从好的方面来看,已经有人努力创建 WGSL 语言的扩展(WESL),它首先将提供一个 import 功能,该功能将解决上述组合问题,并添加诸如条件编译和运行时变量插入之类的其他功能。
将 WebGPU 集成到 ZK 框架中
优化计算与数据传输
通常,GPU 上的计算速度快且具有成本效益,而 CPU 和 GPU 之间的数据传输可能是一个主要的瓶颈(基准测试)。 在 zk 电路或 zkVM 中,这可能意味着将整个证明过程卸载到 GPU,而不是卸载多个组件,尤其是在输入和输出数据相对于生成的中间数据较小时。
另一个需要考虑的因素是,移动设备 GPU 可以访问的内存量各不相同,为了支持各种移动设备,应该提供一种混合方法来决定何时使用 GPU 或何时不使用 GPU。 WebGPU 有一个 API 公开了底层设备 GPU 可以访问的最大内存大小,该 API 可用于确定 GPU 是否能够运行计算。
对原生构建的考虑
但是,当以原生构建而不是浏览器为目标时,数据传输的成本会降至接近于零。 这是因为许多现代移动设备对 CPU 和 GPU 使用统一的内存,因此在传输数据时无需将其复制到单独的缓冲区。 (Ingonyama 有一个很好的 POC 用于在 Apple Silicon 上演示这一点)
尽管 WebGPU 为这种情况提供了一个 配置,但开发人员仍然必须实施安全措施,因为并非所有设备都共享统一的内存。
动态调用
WebGPU 的灵活性使其适用于高端和低端设备。 为了充分发挥其潜力,实现应根据设备的限制进行动态调整。 一种基本方法是为 GPU 使用设置最低功能阈值,而更复杂的方法可以根据内存限制在 GPU 上有选择地运行不同的组件。
将 WebGPU 集成到 ZK 中的挑战
高维护成本
将现有的证明代码移植到 WGSL,随着原始实现的不断发展而不断更新它,并进行额外的审计可能需要耗费大量资源。 并且随着新的 zkVM、zkDSL 和新的理论突破不断涌现,将不可能跟上维护成本。 一种潜在的解决方案是构建一个生产就绪的常用着色器例程库(类似于 Ingonyama 的 ICICLE),这将简化集成并减少重复的工作。
缺乏基准测试和测试框架
我们还缺乏用于衡量 ZK 框架性能的基准测试,这将有助于衡量运行证明器时的峰值内存使用量,并确定电路的大小(在 zk 电路的情况下)或程序的大小(在 zkVM 的情况下)应该是多少,才能使其能够使用 WebGPU 运行。 一旦将 WebGPU 集成到 ZK 框架中,拥有跨多个移动设备的测试框架也将使准确评估性能提升变得更加容易。
结论:WebGPU 在 ZK 中的未来之路
正如本文开头所讨论的那样,客户端证明是解锁保护隐私的零知识应用程序的关键,而 WebGPU 正在成为加速这一过程的强大工具。 通过利用 GPU 并行性,我们可以卸载并加速证明中计算最密集的方面。
尽管存在高维护开销和当前缺乏全面的基准测试等挑战,但前进的道路充满希望。 协作努力(例如开发共享着色器库和统一的测试框架)可以克服这些障碍。 随着社区的共同努力,我们可以期待为每个人提供更高效、可扩展和易于访问的隐私解决方案。
- 原文链接: blog.zksecurity.xyz/post...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 177 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 376 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 297 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 394 浏览
- Zcash:比特币遗忘的隐私 442 浏览
- ZK编年史:计算模型 312 浏览
- lambdaworks 2026 年更新路线图和优先级 382 浏览
- 2026年构建机构级DeFi平台真正需要什么 934 浏览
- zkMesh:2026年1月回顾 463 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 672 浏览
- Zcash 的时代到来了 801 浏览
- ZK 编年史:电路(第二部分) 432 浏览

