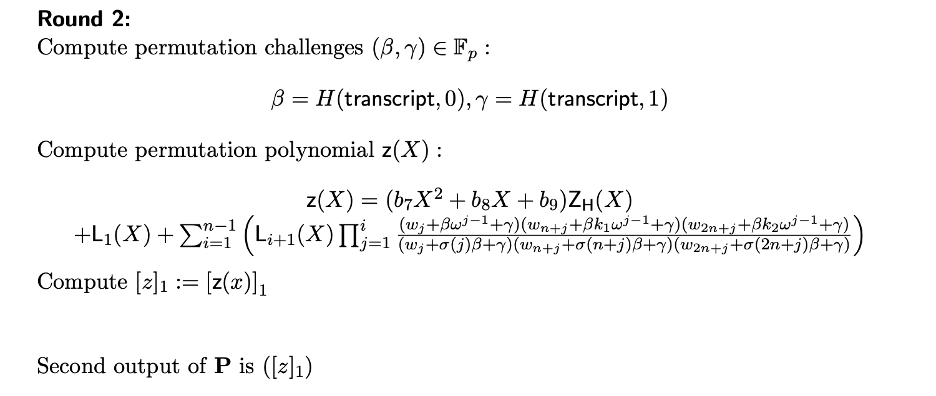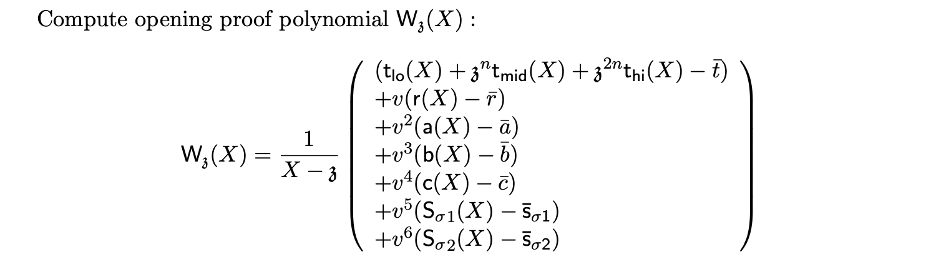PlonK 中的冰封之心漏洞

在本文的第 1 部分 中，我们披露了会破坏零知识证明系统多个实现健全性的关键漏洞。这类漏洞，我们称之为“冰冻之心”（Frozen Heart），是由 Fiat-Shamir 转换的不安全实现造成的，这些实现允许恶意用户伪造随机语句的证明。在博文的第 2 部分 和第 3 部分 中，我们演示了如何在两个特定的证明系统中利用 Frozen Heart 漏洞：Girault 的知识证明 和 Bulletproofs。在本文中，我们将研究 PlonK 中的 Frozen Heart 漏洞。

零知识证明和 Fiat-Shamir 转换

这篇文章假定你已经熟悉零知识证明。如果你想阅读更多关于它们的内容，有很多有用的博文和视频可供你选择，例如 Matt Green 的入门读物。要了解更多关于 Fiat-Shamir 转换的信息，请查看我写的博文，其中更详细地解释了它。你也可以查看 ZKDocs，以获取有关这两个主题的更多信息。

PlonK

PlonK 证明系统是近几年开发的最新 ZK-SNARK 方案之一。SNARK 本质上是一组专门的零知识证明系统，它具有非常高效的证明大小和验证成本。有关 SNARK 的更多信息，我强烈建议阅读 Zcash 的博客系列。

大多数 SNARK 需要一个可信设置仪式。在这个仪式中，一组参与者生成一组以特定方式结构化的值。重要的是，这组参与者中没有人可以知道这组值的底层秘密（否则证明系统可能会被破坏）。这个仪式并不理想，因为这些证明系统的用户必须相信某个团体诚实且安全地生成这些值，否则整个证明系统是不安全的。

较旧的 SNARK 系统需要为每个程序多次执行此仪式。PlonK 的通用和可更新的可信设置要好得多；只需要一个可信设置仪式即可证明多个程序的语句。

在下一节中，我将逐步介绍完整的 PlonK 协议，以演示 Frozen Heart 漏洞是如何工作的。但是，PlonK 非常复杂，因此本节可能难以理解。如果你想了解更多关于 PlonK 如何工作的信息，我强烈建议阅读 Vitalik Buterin 的博文 并观看 David Wong 的 YouTube 系列。

PlonK 中的 Frozen Heart 漏洞

与 Bulletproofs 一样，PlonK 包含多个 Fiat-Shamir 变换。如果这些变换中的任何一个实现不正确，则可能包含 Frozen Heart 漏洞。我将重点关注一个似乎最常见的特定漏洞。这是影响 Dusk Network 的 plonk、Iden3 的 SnarkJS 和 ConsenSys 的 gnark 的漏洞。

PlonK 与大多数 SNARK 一样，用于证明某个计算已正确执行。在一个称为算术化的过程中，计算以证明系统可以解释的格式表示：多项式和算术电路。

我们可以将计算的输入视为电路中的输入线。对于 SNARK，有公共和私有输入。私有输入是只有证明者才能看到的电路中的线。公共输入是剩余的线，证明者和验证者都可以看到。

其他公共值包括用于生成和验证证明的可信设置仪式生成的值。此外，由于证明者和验证者需要就待证明的计算或程序达成一致，因此程序的电路表示在双方之间公开共享。

在本系列的第 1 部分中，我们介绍了一个安全实现 Fiat-Shamir 变换的经验法则：Fiat-Shamir 哈希计算必须包括零知识证明语句中的所有公共值以及证明中计算的所有公共值（即，所有随机“承诺”值）。这意味着公共输入、来自可信设置仪式的值、程序的电路以及证明本身计算的所有公共值都必须包含在 PlonK 的 Fiat-Shamir 变换中。影响 Dusk Network、Iden3 和 ConsenSys 代码库的 Frozen Heart 漏洞源于它们未能在这些计算中包含公共输入。让我们仔细看看。

PlonK 协议概述

PlonK 自首次发布以来已经过一些修订，因此许多 PlonK 实现并非基于 Cryptology ePrint 存档上的最新版本。在本节中，我将重点关注2020 年 3 月发布的这个版本，因为这（或类似的版本）似乎是 SnarkJS 实现所基于的版本。注意：当协议实现不正确时，此漏洞仍然适用于该论文的所有版本，但对于不同的版本，如何利用此问题的确切细节会有所不同。

(上面的段落在 2022 年 6 月 8 日更新。)

在深入研究协议的细节之前，我将从高层次上描述它。为了生成证明，证明者首先构造一系列对表示计算的各种多项式的承诺（具体而言，它们是与程序的电路相对应的约束）。在承诺这些值之后，证明者构造这些多项式的打开证明，验证者可以使用椭圆曲线配对来验证这些证明。这种多项式承诺和打开是使用 Kate 多项式承诺方案完成的。这个方案很复杂，但它是 PlonK 协议的核心部分，理解它对于理解 PlonK 如何工作至关重要。查看这篇博文 了解更多详情。

从证明者的角度来看，该协议总共有五个轮次，每一轮都计算一个新的 Fiat-Shamir 挑战。以下是 PlonK 协议的所有公共和私有输入：

PlonK 证明系统的公共和私有输入 (来源)

公共预处理输入包含来自可信设置仪式的值（x[1]1, …, xn+2[1]1 值，其中 x[1]1 = g1x 且 g1 是椭圆曲线群的生成元）以及程序的电路表示；这些由证明者和验证者共享。其余的值是程序的电路的输入线。公共输入是公共线，证明者的输入既是公共输入又是证明者的私有线。确定了这一点后，我们可以开始协议的第一轮，证明者在其中计算加盲(blinded)线值。

PlonK 协议中证明者的第 1 轮 (来源)

证明者首先计算三个多项式（a、b 和 c），然后使用来自可信设置仪式的值在点 x 处评估它们。底层的 x 值是未知的（假设可信设置仪式执行正确），因此，证明者正在生成对这些多项式的承诺，而不会泄露任何信息。证明者在第 2 轮中对置换多项式执行相同的操作：

PlonK 协议中证明者的第 2 轮 (来源)

我们将不详细描述这一轮，因为它特别复杂并且与此漏洞无关。总之，这一轮负责实施“复制约束”，确保分配给所有线的值是一致的（即，它阻止证明者分配不一致的值，如果一个门的输出是另一个门的输入）。从那里，证明者在第 3 轮中计算商多项式。正如我们很快就会看到的那样，这个商多项式对于 Frozen Heart 漏洞至关重要。

PlonK 协议中证明者的第 3 轮 (来源)

在第 3 轮之后，证明者然后使用 Fiat-Shamir 技术计算评估挑战 zeta。然后使用 zeta 评估到目前为止构造的所有多项式。这个 zeta 挑战值是我们将要在 Frozen Heart 漏洞中定位的值。正如你所看到的，本文的作者使用了术语“transcript（记录）”，他们在本文的前面解释说，这意味着预处理输入、公共输入和沿途生成的证明值。

(上面的段落在 2022 年 4 月 29 日更新。)

PlonK 协议中证明者的第 4 轮 (来源)

最后，在第 5 轮中，证明者然后生成打开证明多项式并返回最终证明。

PlonK 协议中证明者的第 5 轮 (来源)

要验证此证明，验证者执行以下 12 个步骤：

PlonK 协议中的验证者 (来源)

在高层次上，验证者首先验证证明是否格式良好（步骤 1-4），计算一系列值（步骤 5-11），然后使用单个椭圆曲线配对操作验证它们（步骤 12）。此检查本质上验证了构造的多项式的可除性，并且只有在多项式的结构符合预期时才会通过（当然，除非存在 Frozen Heart 漏洞）。

利用 PlonK 中的 Frozen Heart 漏洞

回想一下，有问题的 Frozen Heart 漏洞源于未能将程序的电路的公共输入包括在任何 Fiat-Shamir 挑战计算中（重要的是，zeta）。在高层次上，恶意证明者可以通过选择恶意公共输入值（这将取决于像 zeta 这样的挑战值）来利用此漏洞，从而欺骗验证者在步骤 8 中重建一个将通过最终验证检查的 t_bar。让我们看看细节。

回想一下，在第 1 轮中，证明者根据证明者的公共和私有线值生成三个多项式（a、b 和 c）。如果我们是一个试图伪造证明的恶意证明者，那么我们实际上没有这些线值（因为我们实际上没有进行任何计算）。因此，在第 1 轮中，我们将生成完全随机的多项式 a’、b’ 和 c’，然后输出它们的评估值 [a’]1、[b’]1 和 [c’]1。

我们的随机 a、b 和 c 多项式将破坏在第 2 轮中计算的多项式，因为这个多项式实施了“复制约束”，这意味着线值是一致的。使用完全随机的多项式，基本上可以保证这些约束不会成立。幸运的是，我们可以通过将第 2 轮多项式归零并输出 [0]1 来完全跳过这些检查。注意：如果实现检查无穷远点，则验证者可能会拒绝此证明。如果是这种情况，你可以巧妙地生成 a’、b’ 和 c’，以便复制约束成立，但其工作方式的细节有点令人讨厌。由于 SnarkJS 实现 不会在此归零多项式上返回错误，因此我将继续使用此方法。

现在，对于第 3 轮，请记住，我们没有所需的线值来正确计算我们的多项式 t。相反，我们将生成一个随机多项式 t’ 并输出 [t’lo]1、[t’mid]1 和 [t’hi]1。

在第 4 轮中，我们将像以前一样计算挑战(challenge) zeta 和所有评估，除了我们现在使用 a’、b’、c’ 和 t’。然后，我们将以预期的方式使用这些评估来构造 r 多项式，然后在 zeta 处评估 r 并输出所有评估。请注意，计算的每个评估都与我们在前几轮中承诺的多项式一致。

在第 5 轮中，我们将按预期执行计算，但将 a、b、c 和 t 替换为 a’、b’、c’ 和 t’。这是协议的结束，但我们还没有完成。最后一步是计算将欺骗验证者的公共输入值。

欺骗验证者实际上归结为这个打开证明多项式（我们可以忽略另一个打开证明多项式，因为我们在第 2 轮中将多项式 z 归零）：

打开证明多项式的计算 (来源)

由于我们在第 4 轮中的评估对应于在第 5 轮中使用的多项式，因此当在 zeta 处评估时，上面大括号内的多项式将评估为零；因此，它可以被 (X - zeta) 整除，我们可以计算 Wzeta。现在，我们需要确保我们在证明中计算的值由验证者以相同的方式重新计算。在步骤 9-11 中，验证者以与证明者计算它们的方式相同的结构重建这些值。因此，所有这些值都应该是有效的。

这只给我们留下了一个最终问题需要在步骤 8 中解决，验证者在其中计算 t_bar。因为我们输出 t’_bar，t_bar 是一个在 zeta 处评估的随机多项式，而不是证明者应该计算的 t_bar，所以验证者的 t_bar 将与我们的输出不匹配，并且不会通过验证。但是，验证者使用公共输入来计算 t_bar，这些公共输入未包含在任何挑战（即 zeta）的 Fiat-Shamir 变换中。因此，我们可以改造我们的公共输入，以便它们强制验证者在步骤 8 中计算 t’_bar。

为此，我们首先将我们在第 4 轮中计算的 t’_bar 插入到步骤 8 中等式的左侧。然后，我们求解这个等式以得到 PI(zeta)，即公共输入乘以拉格朗日多项式的和。由于它是总和，因此有多种组合可以使用。最简单的方法是将除第一个之外的每个公共输入都归零，并求解导致我们求解的 PI(zeta) 值对应的线值。我们现在已经构造了我们的公共输入，这将欺骗验证者计算 t’_bar。这样做的原因是这些公共输入值不用来计算 zeta，所以我们知道 zeta 在我们必须决定这些公共输入值之前。

现在，验证者将重建我们在第 4 轮中计算的相同 t’_bar 值，并且最终的配对检查将通过——我们已成功伪造了一个证明。

需要明确的是，此漏洞仅通过不正确的实现引入；这不是 PlonK 论文本身的漏洞。

(本节已于 2022 年 4 月 29 日更新。)

Frozen Heart 对 PlonK 的影响

让我们退一步，评估这个漏洞的严重性。首先，让我们回顾一下我们正在证明的内容。使用 PlonK，证明者正在向验证者证明他已正确执行特定的（商定的）程序，并且他已提供给验证者的输出是正确的。在上一节中，我们通过使用程序的电路的完全随机的线值伪造了一个证明。验证者接受此计算证明是有效的，即使证明者没有正确计算任何电路的线值（即，他实际上没有运行该程序）。值得重申的是，这篇文章只关注一种 Frozen Heart 漏洞。如果其他 Fiat-Shamir 转换未正确完成，则可能对此证明系统进行几次类似的攻击。

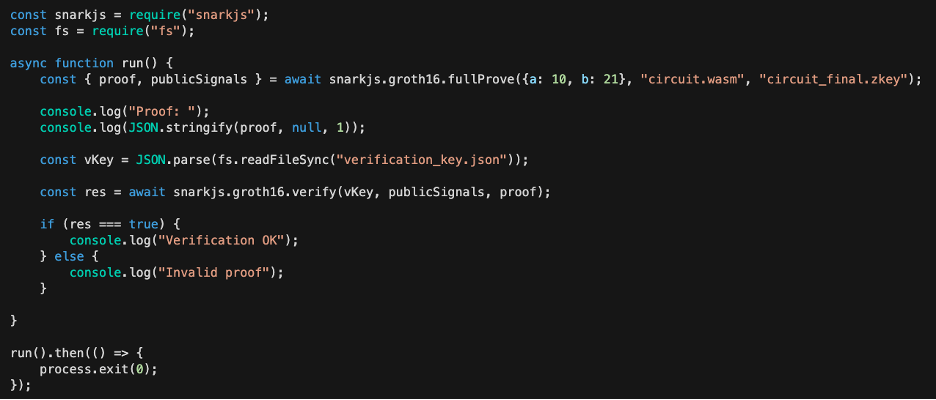
这是否在实践中可利用取决于验证者如何处理公共输入值。具体来说，只有在验证者接受来自证明者的任意公共输入（而不是例如事先商定它们）的情况下，才可以利用它。如果我们查看 SnarkJS 存储库中的示例代码，我们可以看到公共输入（publicSignals）由证明者输出（使用 fullProve 函数）并且被验证者盲目接受（此示例适用于 Groth16，但 PlonK API 的工作方式相同）。通常，此漏洞的可利用性取决于具体实现。

使用 SnarkJS 的示例代码段 (来源)

你可以想象，在大多数应用程序中，这种类型的证明伪造非常严重。PlonK 证明系统有效地没有提供任何关于程序已正确执行的保证。请记住，我们的示例使用了随机线值，但这不是必需的。更复杂的攻击者可以选择更巧妙的线值（例如，通过选择有利于攻击者的程序的输出）并且仍然执行相同的攻击。

这是我们关于 Frozen Heart 漏洞系列的最后一篇文章。我希望到目前为止，我已经清楚地表明这些问题非常严重且不幸地普遍存在。我们希望这一系列文章能够提高对这些问题的认识。如果你还没有这样做，请查看 ZKDocs 以获得更多指导，如果你希望添加更多内容，请联系我们！

• 原文链接： blog.trailofbits.com/202...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～