全同态加密与真正隐私互联网的曙光

  • bozmen
  • 发布于 1天前
  • 阅读 216

本文深入探讨了全同态加密（FHE）技术，该技术允许在加密数据上进行计算而无需先解密，从而确保数据在整个生命周期中的隐私。文章讨论了FHE的工作原理、性能改进以及其在云计算、LLM推理和区块链智能合约等领域的潜在应用，强调了FHE技术正快速发展，或将推动互联网隐私保护进入新时代。

"在互联网上使用加密技术，相当于安排一辆装甲车将信用卡信息从住在纸板箱里的人送到坐在公园长椅上的人手中。" -- Gene Spafford

想象一下，你向 Google 发送一个加密的问题，然后得到你想要的精确结果——而他们没有任何方法知道你的问题是什么，或者他们返回的结果是什么。实现这一点的技术被称为 全同态加密 (FHE)。

我第一次听说 FHE 的作用时，我不相信这是可能的。但它确实存在——并且今天在 现实世界的系统中 运行。

它允许对 ciphertext（加密数据）进行任意计算——而无需先对其进行解密。计算的结果，一旦解密，就与在 plaintext（未加密数据）上执行的结果相匹配。

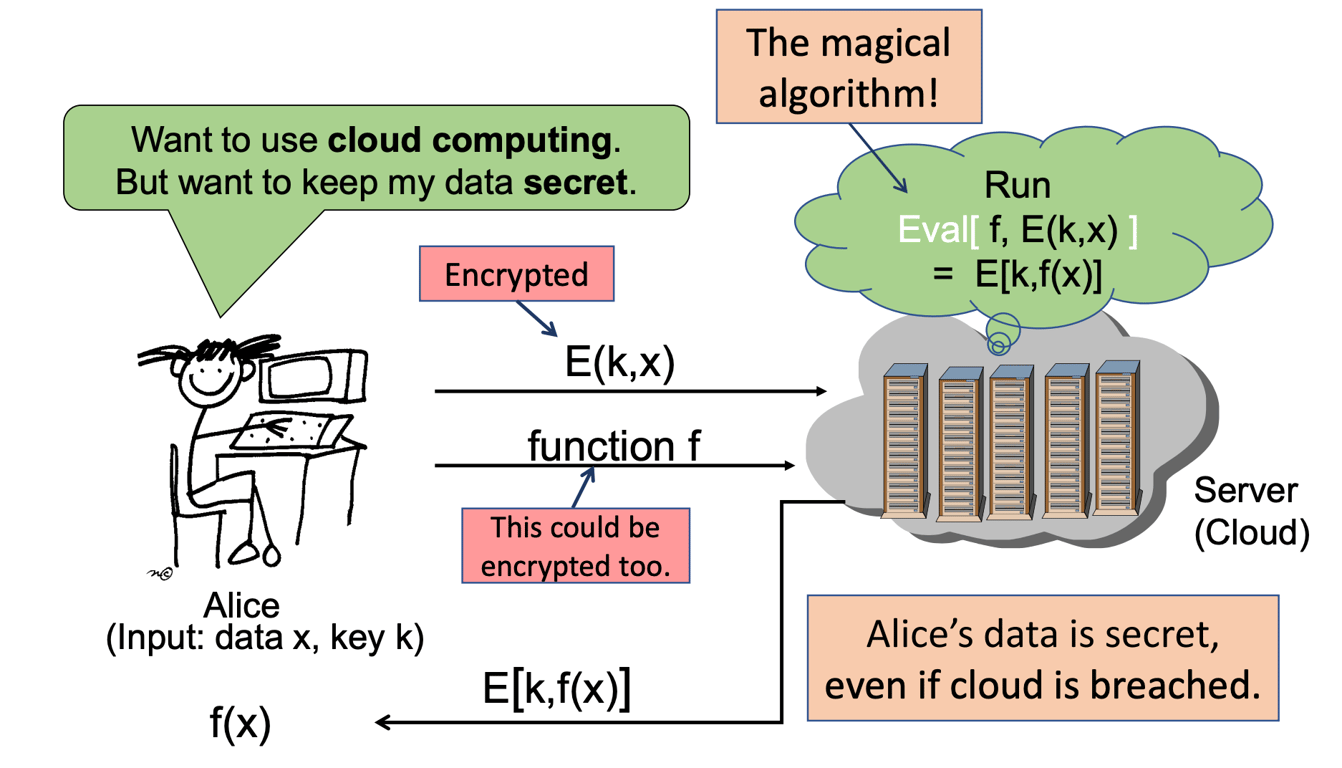
Pasted image 20250715025822.png

FHE 的摩尔定律

由于 FHE 允许加密计算，用户可以始终在互联网上保持其数据加密（发送、服务器计算、接收返回）。这可以防止任何数据泄露的机会。完全隐私。

但是，为什么它不像 HTTPS 那样是默认设置？为什么不是每个人都在使用它？为什么大多数人甚至都没听说过它？

因为它对于大多数应用程序来说仍然不实用，因为它非常慢。但是，正如我将在下面解释的那样，这种情况正在迅速改变。

与 plaintext 操作相比，当前的 FHE 具有 1,000 倍到 10,000 倍的计算开销。在存储方面，ciphertext 可能比原始数据大 40 到 1,000 倍。这就像 1990 年代的互联网——技术上很棒，但在实践中受到限制。

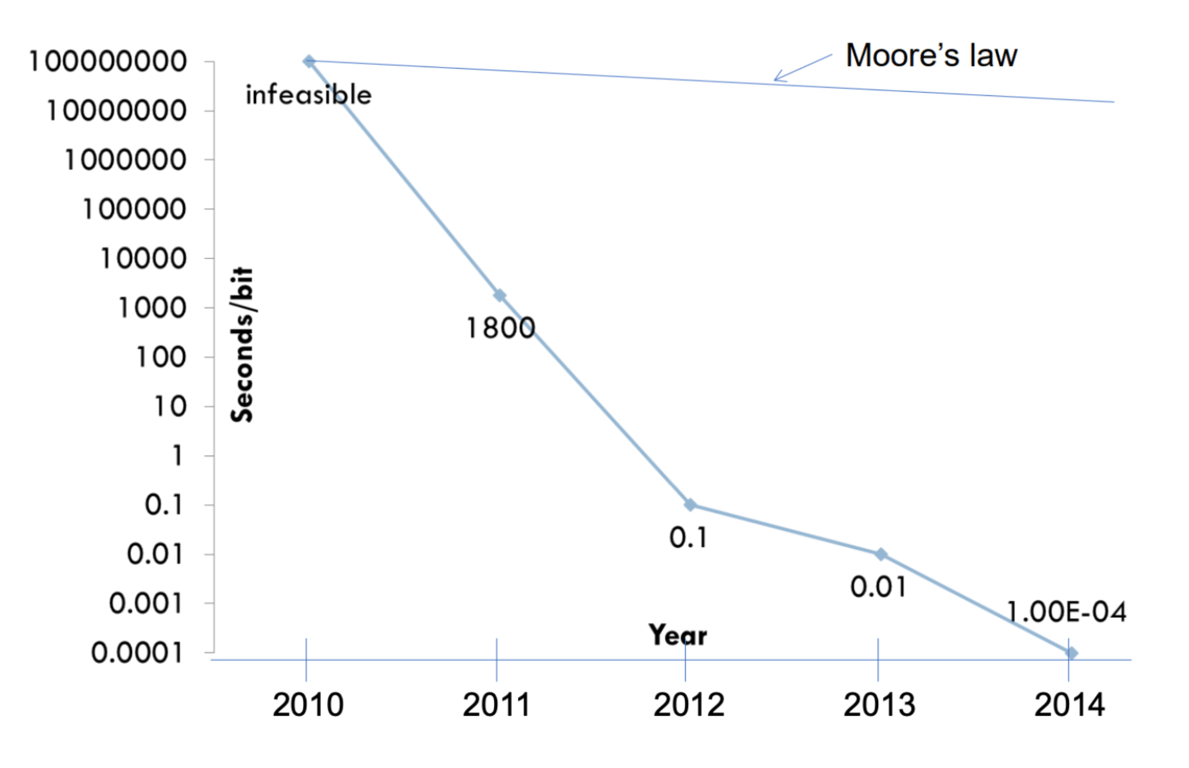
有趣的地方来了：FHE 算法每年都快 8 倍。 在 2011 年每比特需要 30 分钟的操作现在只需要几毫秒。请参阅下面的图表，显示其显着的速度改进。

Pasted image 20250715211925.pngref

该图显示了直到 2014 年的 10^12 倍的改进。在过去的十年里，改进的步伐也在继续。我将在本文后面更深入地介绍这一点。

拐点

如果这种显着的改进继续下去，我们正在接近一个计算拐点。在不久的将来，FHE 可能足够快，可以用于：

  • 加密云计算

  • 加密 LLM 推理

  • 机密区块链智能合约

其影响是巨大的。建立在收集用户数据之上的整个商业模式可能会过时。当另一项服务可以在你的 ciphertext 上进行计算时，为什么还要发送你的 plaintext？

互联网的“默认监视”可以变为“默认隐私”。

Pasted image 20250715025158.pngref

深入探讨

以下部分将更深入地探讨本文主张的各个方面。如果你对这些部分特别好奇，你可以跳到任何一个部分。你也可以按顺序阅读它们，因为它们是按照逻辑顺序排列的：

  • 问题：安全性的阿喀琉斯之踵

  • 解决方案：定义完全隐私计算

  • 技术深入：FHE 实际是如何工作的

  • 更多关于性能改进：FHE 的摩尔定律：每年快 8 倍

  • 连接各个点：计算的未来是加密的

安全性的阿喀琉斯之踵

所有数据都存在于三种状态之一：

  1. 静态（存储在磁盘上）

  2. 传输中（通过网络移动）

  3. 使用中（在内存中处理）

我们对前两个有强大的解决方案：

  • 静态： 磁盘加密、文件系统加密。

  • 传输中： TLS/SSL、VPN、端到端加密。

但是使用中——当数据加载到 RAM 中并由 CPU 处理时——它是解密的。这是现代安全性的阿喀琉斯之踵。云提供商、内部人员、攻击者或受感染的 CPU 可以读取你的 plaintext 数据。

Pasted image 20250714224822.png

想想你听过的每一个重大数据泄露事件：

它们都是使用中或静态加密的失败。当数据加载到内存中进行处理时，它就变得脆弱。

FHE 解决了这个问题。数据可以在云上的整个生命周期中保持加密，我们可以称之为“完全隐私计算”。

定义完全隐私计算

想象一下这样一个互联网，你的数据始终是加密的：

  • 静态加密

  • 传输中加密

  • 使用中加密

这意味着：

  • 你的设备永远不会将 plaintext 发送到任何服务器

  • 服务器只处理加密数据

  • 只有你可以解密结果

以下是一个私密的 ChatGPT 会话的样子：

## 你的设备
pk, sk = keygen() # pk: public key, sk: secret (private) key
enc_prompt = encrypt("为什么开发人员要去接受治疗？", pk)
server.send(enc_prompt, pk)

## OpenAI 的服务器（他们永远无法解密并看到你的提示）
enc_prompt, pk = client.receive()
enc_llm = encrypt(LLM_MODEL, pk)
enc_answer = enc_llm.run(enc_prompt)
client.send(enc_answer)

## 你的设备再次
enc_answer = server.receive()
answer = decrypt(enc_answer, sk)
print(answer)
"""因为有太多未解决的依赖项！"""

OpenAI 计算出正确的响应，但永远无法以 plaintext 形式看到你的问题或他们的答案。

隐私作为一种计算不变量。

FHE 如何工作

术语“同态”来自希腊语：“homo”（相同）+“morphe”（形式）。它意味着在两个代数结构之间具有保结构的映射。FHE 是同态的，因为对加密数据的操作可以映射（即镜像）到对原始数据的操作上。

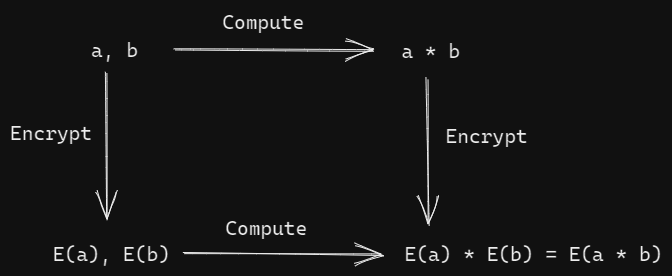
范畴论中的同态通常由交换图表示，你可以通过交换运算顺序从一个点到达另一个点。在下面 FHE 的图表中，你可以通过两种不同的方式从 (a, b) 到达 E(a*b)。

Pasted image 20250715154332.pngref

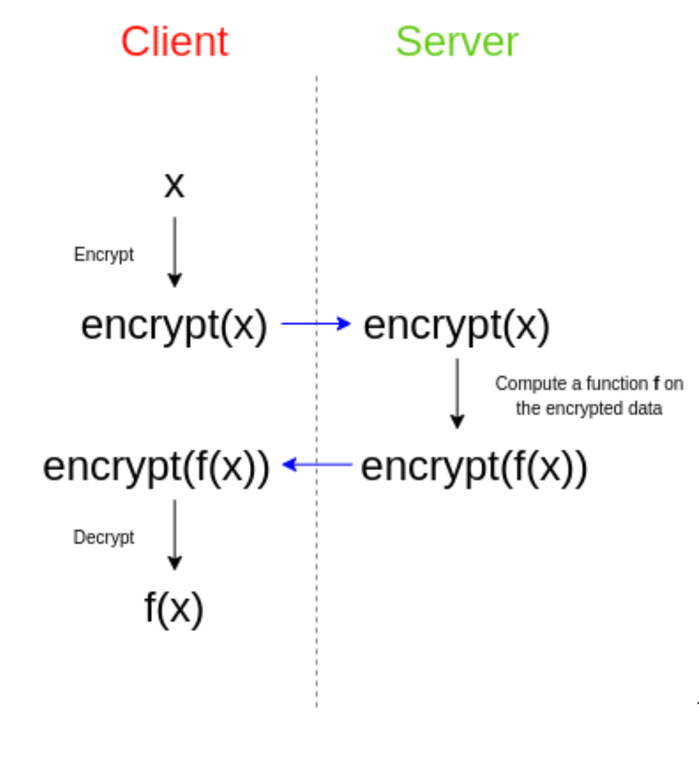
让我们看看一个具有客户端/服务器视角和 f(x) 函数的等效图。

Pasted image 20250715030530.pngref

一个有用的 FHE 类比是 傅里叶变换，它将信号从时域转换为频域。在频域上执行的计算等效于在时域中执行的计算，反之亦然。这意味着你可以在任何一个域中进行计算，并且仍然获得相同的结果。以类似的方式，FHE 在 plaintext 和 ciphertext 域之间运行。在 plaintext 域中完成的转换等效于在 ciphertext 域中完成的转换，反之亦然。

双向转换
傅里叶变换 时域 <--> 频域
FHE plaintext 域 <--> ciphertext 域

基于格的密码学

为了进行上述转换，FHE 使用 基于格的密码学——想象一个在所有方向上无限延伸的多维点网格。

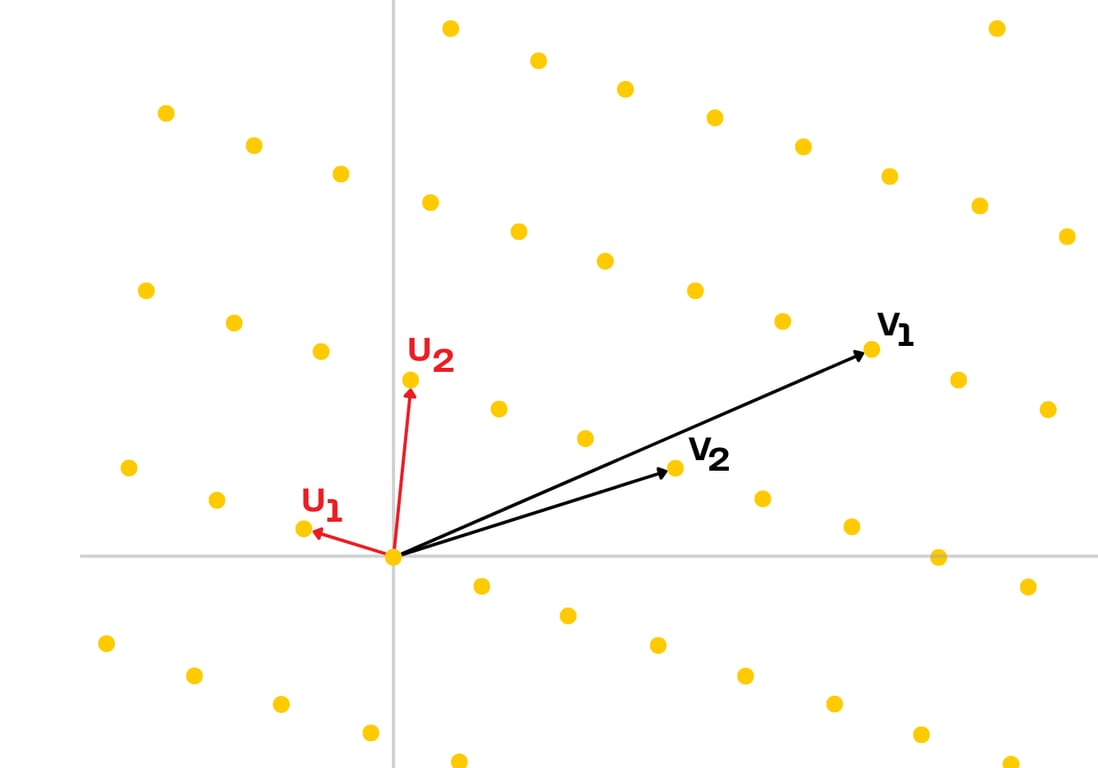
Pasted image 20250713001202.png

基于格的密码学的核心是那些被认为极其难以解决的问题——即使对于量子计算机来说也是如此。两个最著名的例子是 1：：

  • 最短向量问题 (SVP)： 找到晶格点之间的最短路径

  • 最近向量问题 (CVP)： 找到最接近任何给定点的晶格点

在 2D 中，这些看起来很简单。但是添加 1,000,000 个维度呢？然后它变得极其困难，以至于人们认为 即使是量子计算机也无法有效地破解它们。这使得 FHE 本质上具有抗量子性。一个非常重要的属性，可以为可能的量子计算未来做好准备。

奖励：晶格运算是高度可并行化的，这意味着它们从现代 GPU 和专用硬件加速中获益匪浅。

带误差学习 (LWE)

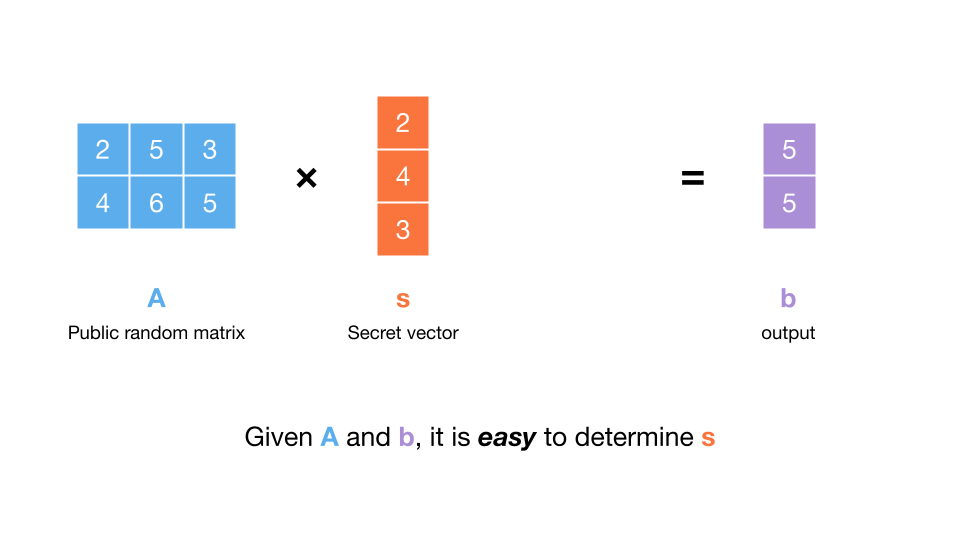
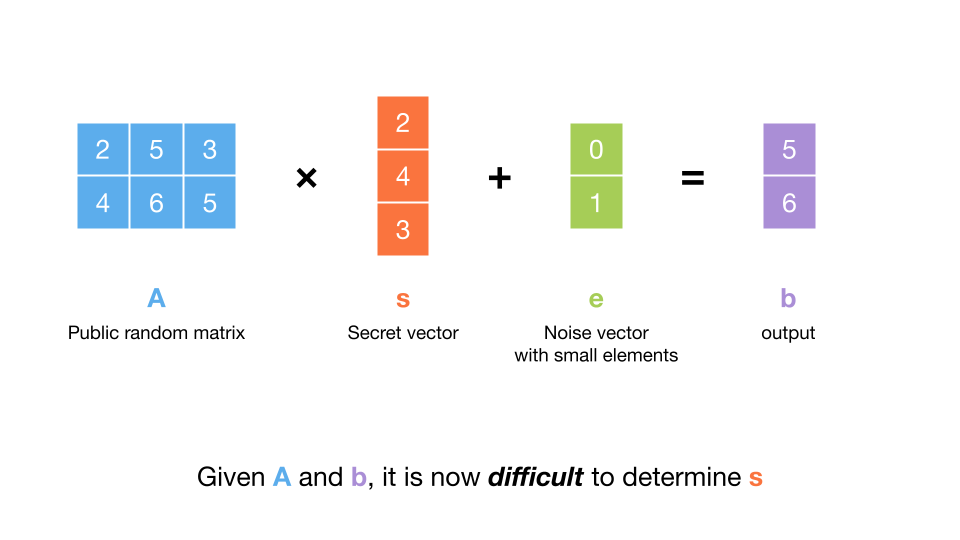
基于格的 FHE 方案依赖于 带误差学习 (LWE) 或 环 LWE 问题。在高层次上，LWE 看起来像这样：

A -> 一个已知的矩阵

s -> 密钥

e -> 随机小噪声

计算 b = A*s + e (即 b 是一个带噪声的线性组合)

生成公钥 = (A, b)

难点： 给定公钥 (A, b)，找到密钥 s

Pasted image 20250716154600.pngPasted image 20250716154635.pngref

请注意，A*s 是线性的，因此在视觉上形成一个晶格。换句话说，A*s 在一个晶格点上。噪声 e 的添加使得结果 A*s + e = b 从晶格点漂移（请注意，噪声是从一个窄随机分布中采样的，因此 b 不会从晶格点漂移太多，因此它更接近另一个晶格点）。

因此，问题变成了：如果攻击者想要从公钥 (A, b) 中找到密钥 s，他需要解决找到最近晶格点的问题 = 最近向量问题 (CVP)。并且最近向量问题被认为是 NP 难题，甚至 抗量子。

总而言之，加密是由于噪声而工作的。并且加密保持安全，因为解码带噪声的晶格点是困难的。

噪声管理和引导

虽然噪声是这里的技巧，但它也会在加法和乘法运算期间导致以下问题。在同态加法期间，每个 ciphertext 的噪声也会相互相加，而在乘法期间，它们相乘。这导致：

  • 加法 --> 噪声线性增长 (可管理)

  • 乘法 --> 噪声成倍增长 (不可管理)

如果噪声变得太大，解密就会失败——你会得到垃圾而不是结果。

由于噪声增长在乘法中是不可管理的，因此在 Craig Gentry 2009 之前的基于噪声的 HE 方案只允许有限数量的乘法（因此不是图灵完备的）。因此，它们被称为 半同态加密。

Craig Gentry 在 2009 年发明 了第一个 HE 方案，该方案允许无限数量的加法和乘法组合。因此它是 图灵完备的。因此它被称为全同态加密。请注意，任何类型的计算都可以表示为加法和乘法。实际上，所有计算都简化为 CPU/GPU 级别的加法和乘法。

使 FHE 工作的关键部分是称为“引导”的方法。引导在噪声变得太大时减少噪声。通过这种方式，它可以保证噪声不会扰乱解密，无论执行多少次乘法。

引导的工作方式非常聪明。它可能被称为“引导”，因为它在另一个公钥下“刷新”了 ciphertext。它巧妙地将 ciphertext 从一个公钥切换到另一个公钥，如下所示：

  1. 获取原始公钥 pk_orig

  2. 获取最初在 pk_orig 下加密的 ciphertext ctx

  3. 生成一个全新的密钥对 pk_new, sk_new

  4. 在 pk_new 下加密 pk_orig，获得 pk_bootstrap (没错！用另一个密钥加密密钥。有创意！)

  5. 在 pk_new 下加密 ciphertext ctx，获得 ctx_new

  6. 通过 sk_new 对 ctx_new 运行（同态）解密操作，获得 ctx_bootstrap

请注意，FHE 的解密过程本身就是一种计算。因此它也可以用于同态计算！

新的 ctx_bootstrap 是另一个新的 ciphertext，其噪声被重置。请注意，它在解密计算过程中经历加法和乘法时获得了一些固定的噪声。但是此噪声是有界的。

需要记住的另一件事是，引导是现代 FHE 方案的性能瓶颈。尽管通过新算法，其计算开销每年都在提高。

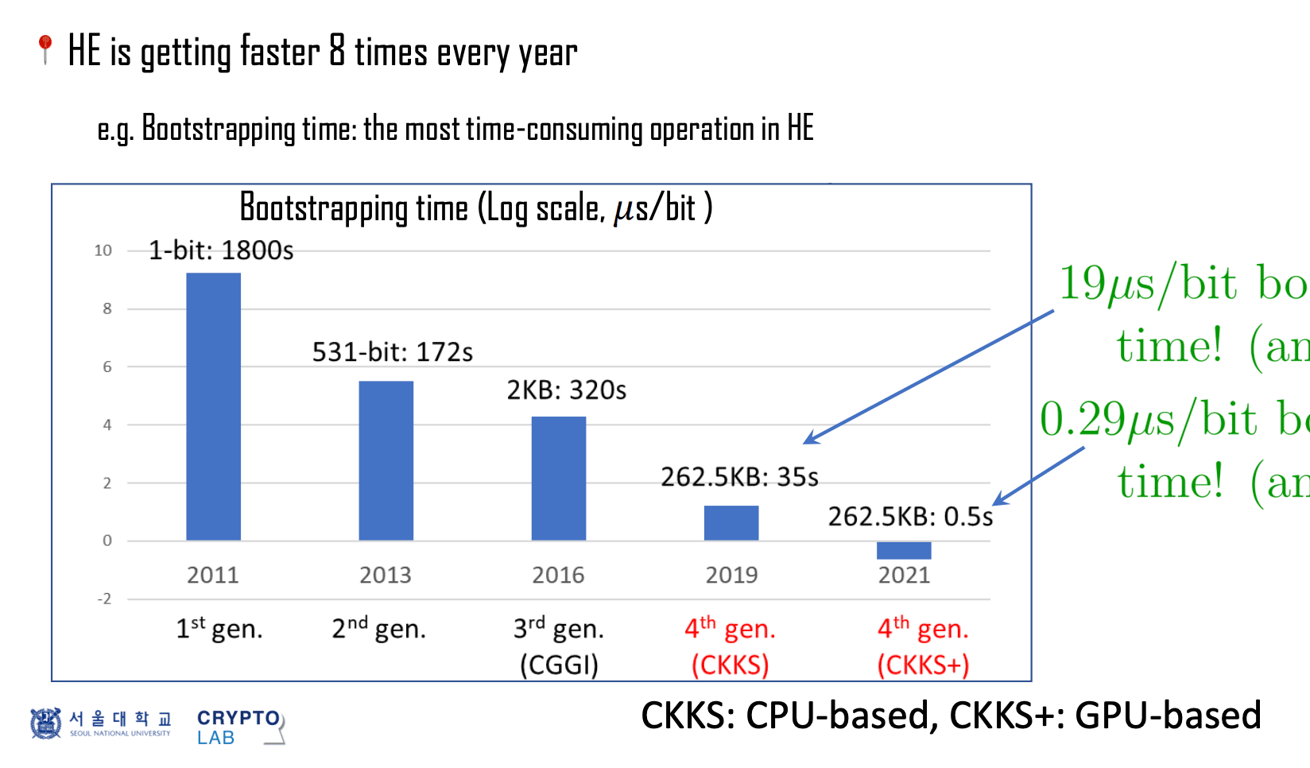
Pasted image 20250712053657.png

还有很多细节。我列出了一些 FHE 引导 的资源，虽然它们也没有涵盖所有内容。人们需要阅读 FHE 参考库。围绕引导的其他主题非常复杂，而且据我所知，它是 FHE 算法创新的重点。至少从概念上理解它非常重要，因为它是 FHE 缓慢的根源，同时也是 FHE 工作的根本原因。

你需要了解的关于 FHE 的其他主题是 重线性化 和 模切换。 我将在这里仅凭直觉来解释它们。对于更深入的数学，我建议 Vitalik 的帖子 作为入门。

重新线性化

ciphertext 在密钥中是线性的 -> a + b​⋅s

乘法后，结果在密钥中变为二次方。为了说明这一点：

让我们乘以下面的 ciphertext：

  • ct1 = (a1, b1) 其解密形式为 a1 + b1*s

  • ct2 = (a2, b2) 其解密形式为 a2 + b2*s

乘法后：

  • ct_mul = (a₁a₂, a₁b₂ + a₂b₁, b₁b₂) 其解密形式为 a₁a₂ + (a₁b₂ + a₂b₁)·s + b₁b₂·s²

  • 请注意 s² 项，这使得 ct_mul 在密钥中是二次方的。

重新线性化使用称为“重新线性化密钥”的额外公钥材料来消除高阶项。过程：

  1. 获取二次项 b₁b₂·s²

  2. 使用重新线性化密钥将此项“转换”回线性项

  3. 生成一个新的线性 ciphertext (c₀', c₁')，它解密为相同的值

模切换

它用于管理噪声增长。这是一种通过降低 ciphertext 的模数来降低噪声的技巧。

我与 ChatGPT 进行了一些对话，以更好地了解 FHE 的一些数学细节，并将我从它们那里学到的内容 写在这里。

HE 方案的分类

我们所说的同态加密 (HE) 方案是什么意思？

HE 方案是一种密码学构造，它定义了如何执行加密、解密和同态运算（例如 BGV、CKKS、TFHE）。

同态加密方案根据它们支持的运算类型和数量进行分类。

部分同态加密

仅支持一种运算（例如，Paillier 中的加法，RSA 中的乘法）。

（我将构建一个玩具 Pailler 示例在下面，其代码简短而直观）

半同态加密

支持加法和乘法，但允许的乘法次数有限。

（我在上一节中解释了噪声增长如何限制了可能的乘法次数）

全同态加密

支持无限的加法和乘法。图灵完备。通过定期通过引导进行降噪来管理噪声。

一个玩具示例

真正理解计算概念的最佳方法之一是从头开始构建它，以最小的方式。

就本博客文章而言，创建一个全同态加密方案将非常冗长。相反，我们将编写 Paillier HE，它更短，更容易理解，以便获得直觉。Paillier 是一种部分 HE，这意味着它不支持所有运算（因此不是完全 HE）。它仅支持加法（因此是加法同态）。我们将遵循一个典型的 HE 流程：

  1. 密钥生成（公钥 + 私钥）

  2. 数据加密（使用公钥）

  3. 计算（同态运算）

  4. 结果解密（使用私钥）

fhe-toy-implementations

部分 HE (Paillier) - 加法同态

import sympy, random

def generate_keypair(bit_length=512):
    p = sympy.nextprime(random.getrandbits(bit_length))
    q = sympy.nextprime(random.getrandbits(bit_length))
    n = p * q
    g = n + 1
    lambda_ = (p - 1) * (q - 1)
    mu = sympy.mod_inverse(lambda_, n)
    return (n, g), (lambda_, mu)

def encrypt(m, public_key):
    n, g = public_key
    r = random.randint(1, n - 1)
    return (pow(g, m, n**2) * pow(r, n, n**2)) % (n**2)

def decrypt(c, private_key, public_key):
    lambda_, mu = private_key
    n, _ = public_key
    l = (pow(c, lambda_, n**2) - 1) // n
    return (l * mu) % n

def homomorphic_sum(a, b, public_key):
    return (a * b) % (public_key[0]**2)

public_key, private_key = generate_keypair(128)

enc1 = encrypt(5, public_key)
print(enc1) # 75042696080311881003721105285833023546234037256871189406054603593273414107194675808782154359890875636008219678257354647151456750847402457204123856890

enc2 = encrypt(3, public_key)
print(enc2) # 269297253929306291153284608946414491483346738328838888044406160105950588673820650688249910373352597049965491330298818622410901670587359945691000319758

enc_sum = homomorphic_sum(enc1, enc2, public_key)
print(enc_sum) # 232817745404365921249916946617154013580946738803385878188677616867767489473531493655408124901849935882016399498283109322848069064027287561237823608127

dec_sum = decrypt(enc_sum, private_key, public_key)
print(dec_sum) # 8

这是 colab notebook 链接，供你自己运行和使用。我强烈推荐。它会给你带来宝贵的直觉请注意，ciphertext 在每次运行时都会不同，因为加密过程是不确定的（请注意 random 方法）。上面注释的打印输出来自一次运行，用于显示在 Paillier 下 ciphertext 的外观。

如果我们要构建一个完全 HE，它可以使用类似的 API，包括 generate_keypair、encrypt、decrypt 和 homomorphic_sum，并添加 homomorphic_multiply。但是代码会更长。对于这样的代码，请参见 Vitalik 的 homomorphic_encryption.py 和 matrix_fhe.py。另请阅读 他很棒的深入探讨。

进一步阅读：

FHE 的摩尔定律：每年快 8 倍

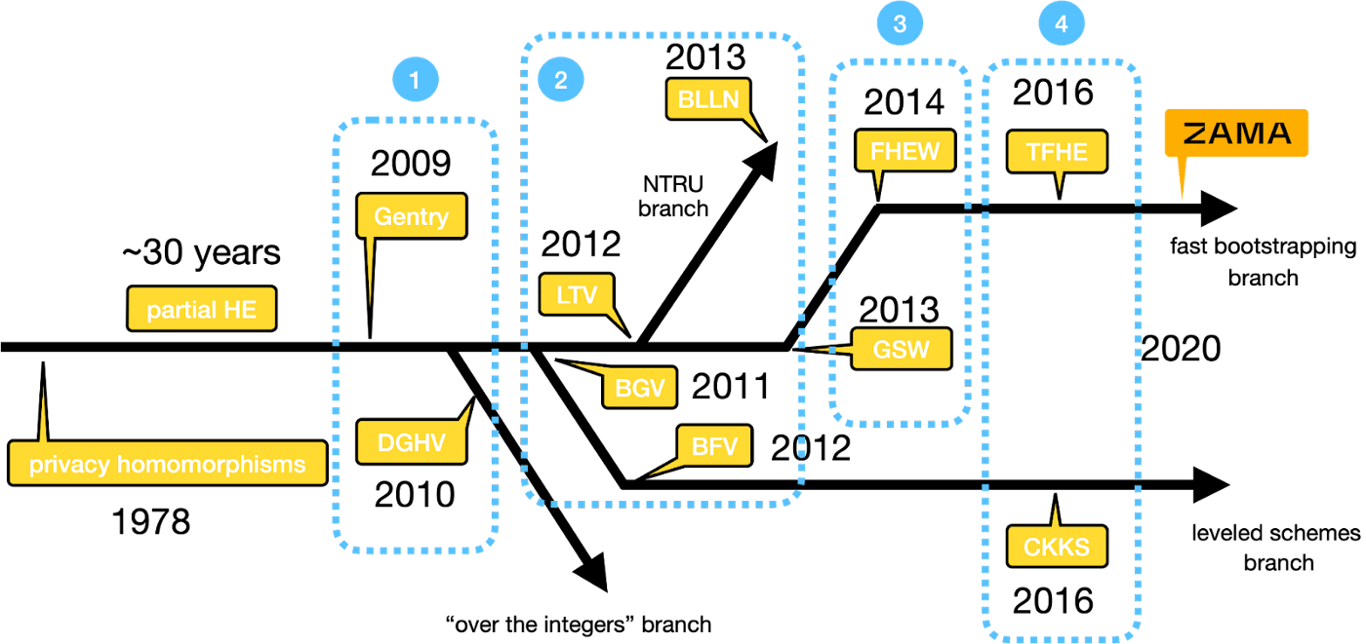
Pasted image 20250710232942.pngref

四个世代：

  • 1978 (史前时代): Rivest、Adleman、Dertouzos 设想了名为“隐私同态”的 FHE

  • 2009 (第一代): Gentry 2009 年的博士论文构建了有史以来第一个 FHE 方案

  • 2011 (第一代): FHE 的首次实施——每个比特的引导花费 30 分钟 2

  • 2011-2012 (第二代): BGV/BFV 方案，基于晶格，仍然很慢。

  • 2013+ (第三代): 更快的引导，以毫秒为单位。

  • 2017 (第四代): CKKS 用于近似浮点数，从而实现 ML/AI。

有关更多信息，请参见 FHE 历史。

Pasted image 20250712053713.png

自 2011 年以来，FHE 性能每年提高 8 倍——从 10¹⁰× 开销下降到今天的 ~10³× ~10^4×。

Pasted image 20250712053657.png

最近的突破正在加速时间表：

  • Dan Boneh 和 Jaehyung Kim 于 2025 年 6 月发表的 论文 声称，高整数运算提高了 1,000 倍的乘法吞吐量和降低了 10 倍的延迟

  • 硬件加速可能会增加 10³× 的加速

除了算法改进外，硬件改进也在发生，从而产生了复合效应。有关更多信息，请参见 FHE 硬件

这是 Vitalik 对进展速度的看法：

exploring-fully-homomorphic-encryption-by-vitalik--archived

我们正在迅速接近这样一个地步，即同态加密在隐私保护计算中的许多应用开始变得实用。此外，对同态加密中使用的基于 lattice 的密码学的更高级应用的研究正在迅速发展。因此，这是一个今天已经可以做一些事情的领域，但我们希望能期待在未来十年中变得更加可能。

计算的未来是加密的

让我们连接各个点。

数据泄露几乎是不可避免的。

保护数据的唯一方法是在服务器上始终对其进行加密，而服务器没有解密的能力。

这意味着即使在对其执行计算时，也应该对数据进行加密。

FHE 支持对加密数据进行计算。

由于其高计算开销，FHE 对于许多应用程序来说还不实用。但它对某些应用程序来说是实用的。

FHE 算法每年都在变得更好，每年提高 8 倍。结果是可行的现实世界应用程序正在增加。FHE 正在蚕食计算，但它仍然很小。

如果这种趋势持续下去，FHE 将征服更多的现实世界用例，以至于大多数云计算都可以通过 FHE 完成。

用户对隐私的意识正在提高。隐私法规正在增加。

如果 FHE 是一种可能的选择，人们和机构将要求它。

如果人们要求它，并且趋势使 FHE 对于大多数计算变得实用，那么大多数互联网计算将基于 FHE。

互联网计算的未来将被加密。不是是否会发生，而是何时发生。

HTTPS by default --> 2010s
FHE by default   --> ?

主要参考文献

主要论文和资源：

来自先驱者：

好文推荐：

改进：

实施范例：

  1. mirror.xyz/0x7a8dEd001067D6f98296df0E9dA2aEE6d75B9494/zwAyC5midnsbwXN-yMg0ykVkJar-OR3zwz2w8xQoMbM - mirror.xyz
  2. news.ycombinator.com/item?id=44601023 - Hacker News
  3. eurocrypt.iacr.org/2021/slides/gentry.pdf - 幻灯片
  4. youtu.be/PfSZL9LsMCg - 大 40 到 1,000 倍
  5. youtu.be/487AjvFW1lk?t=668 - 参考
  6. x.com/VitalikButerin/status/1248704356758753281 - 参考
  7. en.wikipedia.org/wiki/2014_celebrity_nude_photo_leak - 2014 年名人照片泄露
  8. echcrunch.com/2023/12/04/23andme-confirms-hackers-stole-ancestry-data-on-6-9-million-users - 23andMe 基因数据盗窃
  9. en.wikipedia.org/wiki/Capital_One#July_2019_security_breach - Capital One 黑客事件
  10. en.wikipedia.org/wiki/Homomorphism - 同态的
  11. en.wikipedia.org/wiki/Category_theory - 范畴论
  12. vitalik.eth.limo/general/2020/07/20/homomorphic.html - 参考
  13. en.wikipedia.org/wiki/Fourier_transform - 傅里叶变换
  14. www.esat.kuleuven.be/cosic/blog/introduction-to-lattices - 基于格的密码学
  15. www.zama.ai/post/fully-homomorphic-encryption-and-post-quantum-cryptography - 参考]([基于格的密码学
  16. en.wikipedia.org/wiki/Post-quantum_cryptography#Lattice-based_cryptography - 即使量子计算机也无法有效地破解它们
  17. en.wikipedia.org/wiki/Learning_with_errors - 容错学习 (LWE)
  18. en.wikipedia.org/wiki/Ring_learning_with_errors - 环 LWE 问题
  19. blintzbase.com/posts/pir-and-fhe-from-scratch - 参考
  20. en.wikipedia.org/wiki/Post-quantum_cryptography#Lattice-based_cryptography - 抗量子的
  21. www.cs.cmu.edu/~odonnell/hits09/gentry-homomorphic-encryption.pdf - Craig Gentry 2009
  22. digitalprivacy.ieee.org/publications/topics/types-of-homomorphic-encryption - 半同态加密
  23. www.cs.cmu.edu/~odonnell/hits09/gentry-homomorphic-encryption.pdf - 2009 年发明
  24. en.wikipedia.org/wiki/Turing_completeness - 图灵完备
  25. eople.csail.mit.edu/vinodv/FHE/FHE-refs.html - [FHE Bootstrapping|FHE 引导启动]，虽然它们也没有涵盖所有内容。你需要阅读 [FHE Reference Library
  26. vitalik.eth.limo/general/2020/07/20/homomorphic.html - Vitalik 的文章
  27. en.wikipedia.org/wiki/Paillier_cryptosystem - Paillier HE
  28. github.com/vbuterin/research/blob/master/tensor_fhe/homomorphic_encryption.py - homomorphic_encryption.py
  29. github.com/vbuterin/research/blob/master/matrix_fhe/matrix_fhe.py - matrix_fhe.py
  30. vitalik.eth.limo/general/2020/07/20/homomorphic.html - 他精彩的深入探讨
  31. vitalik.eth.limo/general/2020/07/20/homomorphic.html - Exploring Fully Homomorphic Encryption by Vitalik
  32. iamtrask.github.io/2017/03/17/safe-ai - Building Safe AI - A Tutorial for Encrypted Deep Learning - i am trask
  33. www.daniellowengrub.com/blog/2024/01/03/fully-homomorphic-encryption#lwe-to-rlwe-keys - Fully Homomorphic Encryption from Scratch - daniellowebgrub
  34. news.ycombinator.com/item?id=32987155 - HN - Explained from scratch private information retrieval and homomorphic encryption (blintzbase.com)
  35. github.com/barisozmen/tfhe - TFHE 玩具实现
  36. www.youtube.com/watch?v=V3FcM1B4mcg&list=PLnbmMskCVh1cCnWbmgxI0BM0UD2JHH9fz&index=14 - FHE 由内而外
  37. www.youtube.com/watch?v=184NHhE3Kq0 - FHE 的过去、现在和未来
  38. www.youtube.com/watch?v=487AjvFW1lk - FHE 的十年（左右）
  39. medium.com/hashed-official/homomorphic-blockchain-1f7db66ac2f7 - HE 和区块链
  40. www.zama.ai/post/homomorphic-encryption-101 - 参考
  41. eprint.iacr.org/2025/346.pdf - 论文
  42. www.youtube.com/watch?v=V3FcM1B4mcg&list=PLnbmMskCVh1cCnWbmgxI0BM0UD2JHH9fz&index=14 - 10³× 加速
  43. eople.csail.mit.edu/vinodv/FHE/FHE-refs.html - FHE 参考库
  44. crypto.stanford.edu/craig/craig-thesis.pdf - Craig Gentry 的 2009 年博士论文
  45. www.youtube.com/watch?v=V3FcM1B4mcg&list=PLnbmMskCVh1cCnWbmgxI0BM0UD2JHH9fz&index=14 - FHE 由内而外
  46. www.youtube.com/watch?v=184NHhE3Kq0 - FHE 的过去、现在和未来
  47. www.youtube.com/watch?v=487AjvFW1lk - FHE 的十年（左右）
  48. medium.com/hashed-official/homomorphic-blockchain-1f7db66ac2f7 - HE 和区块链
  49. www.youtube.com/watch?v=aruz58RarVA&t=3082s - Introduction to FHE
  50. www.youtube.com/watch?v=TySXpV86958 - 全同态加密从零开始
  51. vitalik.eth.limo/general/2020/07/20/homomorphic.html - Exploring FHE
  52. bowtieditaliano.substack.com/p/fully-homomorphic-encryption-just - 全同态加密变得实用
  53. github.com/barisozmen/securegenomics - FHE for Genomics
  54. uggingface.co/spaces/zama-fhe/encrypted_sentiment_analysis - 加密的情感分析
  55. iamtrask.github.io/2017/03/17/safe-ai - 加密深度学习
  56. iralwiki.com - 私人维基百科
  57. www.jeremykun.com/fhe-in-production - 更多生产示例
  58. fhe.org - FHE.org
  59. www.lesswrong.com/posts/PxMSnEPFG34o9zkq4/what-is-cryptographically-possible - ^1]: 密码系统依赖于 难解问题——那些没有已知多项式时间解的问题（NP-hard）。为了有用，这些问题必须在一个方向上易于计算，但在另一个方向上难以逆转。这些问题被称为 [单向函数
  60. en.wikipedia.org/wiki/One-way_function#Multiplication_and_factoring - 乘法大素数
  • 原文链接： bozmen.io/fhe...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
bozmen
bozmen
江湖只有他的大名，没有他的介绍。

bozmen

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！