格密码学基础（五）（完结篇）：基于Σ-协议构造数字签名

在本节中,我们将努力构造一个基于格的数字签名方案,其高层结构类似于经典的基于离散对数的Schnorr签名方案[Sch89]。在Schnorr数字签名方案中,公钥由有限域中的两个元素$g, h$组成,签名是指数$x$满足$g^x = h$的非交互式零知识知识证明(ZKPoK)。非交互式证明通过两步获得。首先,构造一个3轮交互式$\Sigma$-协议,它是满足$g^x = h$的$x$的诚实验证者ZKPoK。其次,使用Fiat-Shamir变换将交互式证明转换为非交互式证明。

5.1 陈述和见证

我们现在想遵循类似的路线图,从$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$和$\mathcal{R}{q,f}\text{-SIS}{n,m,\beta}$问题构造签名方案。可以从$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$实例$(\mathbf{A}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}2)$开始,其中$\mathbf{A} \leftarrow \mathcal{R}{q,f}^{n \times m}, \mathbf{s}_1 \leftarrow [\beta]^m, \mathbf{s}_2 \leftarrow [\beta]^n$,将$\mathbf{A}, \mathbf{t}$作为公钥,并希望能够创建一个零知识证明来证明对适当范围内的$\mathbf{s}_1, \mathbf{s}_2$的知识。

❝

回忆第4.2节中的记号：对于多项式$s$，$s \leftarrow [\beta]$意味着$s$的所有系数从集合$[\beta] = {-\beta, \ldots, 0, \ldots, \beta}$中均匀随机选择，而$\mathbf{s} \leftarrow [\beta]^n$意味着多项式向量$\mathbf{s}$中的所有$n$个多项式的系数都从集合$[\beta]$中均匀选择。

创建这样的证明结果不如在离散对数设置中那么直接和高效。原因是除了证明$\mathbf{s}_i$满足$\mathbf{As}_1 + \mathbf{s}_2 = \mathbf{t}$的代数关系外,我们还需要证明$\mathbf{s}_i$的系数落在特定范围内(理想情况下是$[\beta]$,但对于某个稍大于$\beta$的$\bar{\beta}$,$[\bar{\beta}]$也可以)。

源自$\Sigma$-协议的最高效签名绕过了证明满足

$$ \mathbf{As}_1 + \mathbf{s}_2 = \mathbf{t} $$

的小$\mathbf{s}_1, \mathbf{s}_2$的知识的需要,而是证明方程的"松弛"解的知识。特别地,我们将给出允许拥有满足上述方程的$\mathbf{s}_1 \in [\beta]^m, \mathbf{s}_2 \in [\beta]^n$的证明者证明$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$的知识的协议,其系数在比$[\beta]$稍大的区间内,以及另一个系数很小的元素$\bar{c}$,满足

$$ \mathbf{A}\overline{\mathbf{s}}_1 + \overline{\mathbf{s}}_2 = \bar{c}\mathbf{t} $$

下面的简单证明表明证明这样的知识仍然证明了一些有意义的东西。特别地,它将使我们可以得出结论:能够产生这样的$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$和$\bar{c}$意味着可以求解与矩阵$\mathbf{A}$相关的环LWE或环SIS。

❝

引理9. 假设存在一个算法,当给定$\mathbf{A} \leftarrow \mathcal{R}_{q,f}^{n \times m}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2$,其中$\mathbf{s}_1 \leftarrow [\beta]^m, \mathbf{s}_2 \leftarrow [\beta]^n$,能够得出$\overline{\mathbf{s}}_1 \in [\bar{\beta}]^m, \overline{\mathbf{s}}_2 \in [\bar{\beta}]^n$和$\bar{c} \in [2]$使得$\mathbf{A}\overline{\mathbf{s}}_1 + \overline{\mathbf{s}}2 = \bar{c}\mathbf{t}$。那么存在另一个算法,运行时间相同,成功概率相同,能够求解$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$或$\mathcal{R}{q,f}\text{-SIS}_{n,m+1,\bar{\beta}}$问题。

证明. 令$\mathcal{A}$为假设中的算法,假设我们被给定均匀随机矩阵$\overline{\mathbf{A}} = [\mathbf{A} \mid \mathbf{t}] \in \mathcal{R}{q,f}^{n \times (m+1)}$,这是$\mathcal{R}{q,f}\text{-SIS}{n,m+1,\bar{\beta}}$问题的一个实例。我们将$(\mathbf{A}, \mathbf{t})$给$\mathcal{A}$。根据$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$假设,这在计算上与$\mathcal{A}$期望的分布不可区分(所以如果$\mathcal{A}$不成功,我们可以用它来求解$\mathcal{R}{q,f}\text{-LWE}_{n,m,\beta}$)。如果$\mathcal{A}$产生系数至多为$\bar{\beta}$的$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2, \bar{c}$满足$\mathbf{A}\overline{\mathbf{s}}_1 + \overline{\mathbf{s}}2 = \bar{c}\mathbf{t}$,那么我们有$\mathcal{R}{q,f}\text{-SIS}_{n,m+1,\bar{\beta}}$实例$\overline{\mathbf{A}}$的解。□

5.1.1 挑战空间

$\bar{c}$(以及$\overline{\mathbf{s}}_1$和$\overline{\mathbf{s}}_2$)中系数的大小将取决于ZKPoK的挑战空间。由于我们希望这些很小,我们想定义挑战空间,使其由范数很小的多项式组成。

如果在环$\mathcal{R}_f$上工作,其中$f$的次数为$d$,那么定义$\eta$为使$2^\eta \cdot \binom{d}{\eta} > 2^{256}$的最小整数(假设$d$足够大以使这样的$\eta$存在)。然后定义挑战集$\mathcal{C} \subset \mathcal{R}_f$为

$$ \mathcal{C} = {c \in [1], |c|_1 = \eta} $$

所有(非零)差的集合为

$$ \overline{\mathcal{C}} = {\bar{c} = c_1 - c_2, \text{ 对于 } c_1 \neq c_2 \in \mathcal{C}} $$

因此$\mathcal{C}$由$\mathcal{R}_f$中所有恰好有$\eta$个非零系数取自集合${-1, 1}$的多项式组成。根据$\eta$的定义,$\mathcal{C}$的大小恰好是$2^\eta \cdot \binom{d}{\eta}$。注意我们可以定义$\mathcal{C}$也包括少于$\eta$个非零系数的多项式,但这会增加在$\mathcal{C}$中采样随机元素的复杂性,同时不会大幅增加其大小。

❝

对长度为 d、包含 η 个 ±1 的随机向量进行采样可以通过以下方式完成：初始化一个 d 维向量，其中包含 η 个 1，然后执行一次洗牌（例如 Fisher-Yates 洗牌）以获得该向量的随机排列，最后随机地对每个 1 进行取反（或不取反）。

5.2 基本$\Sigma$-协议

我们现在描述图5中给出的基本方案,它在[Lyu09]中提出。该协议的一个不寻常特征是它没有完美完备性。为了保持输出系数的小,在$\Sigma$-协议的最后一轮执行拒绝采样步骤,以确保分布独立于秘密。在本教程的所有协议中,拒绝采样步骤将相当简单——只是检查所有系数是否在某个范围内。可以执行稍微复杂一些的拒绝采样步骤,需要根据离散高斯分布进行采样和拒绝,这会导致稍小的输出[Lyu12, DDLL13]。后一种算法的主要缺点是拒绝采样步骤更复杂,稍微不正确的实现可能最终泄露私钥——防御侧信道攻击也可能更复杂。因此,对于像数字签名这样广泛使用的原语,在实践中更简单的算法可能更可取。

私有信息: $\mathbf{s}_1 \in [\beta]^m, \mathbf{s}2 \in [\beta]^n$公开信息: $\mathbf{A} \in \mathcal{R}{q,f}^{n \times m}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}2 \in \mathcal{R}{q,f}^n$

_图5: 基本零知识证明系统,其中证明者知道$\mathbf{s}_1 \in [\beta]^m, \mathbf{s}_2 \in [\beta]^n$,并给出$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}2 \in [2\bar{\beta}]^n$和$\bar{c} \in \overline{\mathcal{C}}$满足知识的ZKPoK。值$\gamma$在引理10中定义,$\bar{\beta}$的值影响协议的完备性(即不发送$\perp$的概率),如引理10中所述。

拒绝采样步骤的主要后果是签名算法的运行时间将是一个随机变量(但独立于$\mathbf{s}_1, \mathbf{s}_2$),而不是固定的。除此之外,熟悉Schnorr型证明的读者会在该协议中发现很多相似之处。协议的第一阶段包括创建掩蔽变量$\mathbf{y}_1$和$\mathbf{y}_2$,第二步是挑战,最后一步包括将掩蔽添加到挑战和秘密的乘积上。然后执行拒绝采样步骤,如果证明者发送$\perp$,他中止并需要重新启动协议。该协议到签名方案的转换将使用通常的Fiat-Shamir变换,其中挑战被创建为消息和证明者的第一条消息的哈希。

在交互式方案中保持通信大小紧凑的一个常见技巧是发送第一条消息的哈希而不是消息本身。因为未哈希的第一条消息可以从下一轮发送的那些中恢复,验证者能够在验证期间计算该消息的哈希。在使用拒绝采样的格设置中,这个技巧还有一个额外的优势,即它将允许我们模拟发生拒绝的脚本。然而,这种哈希对于证明签名方案的安全性是不必要的,因为签名者看不到中止的签名尝试。因此,我们将呈现不带哈希的交互式方案,并仅在没有中止(即没有发送$\perp$)的情况下证明零知识。

5.2.1 诚实验证者零知识

我们现在将证明图5中的协议是HVZK的。即,我们将展示如何在不知道秘密$\mathbf{s}_1, \mathbf{s}_2$的情况下创建有效的脚本。证明的关键是下面的引理,它表明对于所有系数有界的$\mathbf{s}_1, \mathbf{s}_2$,$\perp$的概率相同,并且$\mathbf{z}_1, \mathbf{z}_2$的分布独立于$\mathbf{s}_1, \mathbf{s}_2$。

❝

引理10. 如果$\gamma \in \mathbb{Z}^+$使得对于所有多项式$s \in [\beta], c \in \mathcal{C}$,都有$cs \in [\gamma]$,那么对于图5中协议的所有$\mathbf{s}_i, c$

$$ \begin{gathered} \Pr_{\mathbf{y}_1, \mathbf{y}_2}[(\mathbf{z}_1, \mathbf{z}_2) \neq \perp] = \left(\frac{2\bar{\beta} + 1}{2(\bar{\beta} + \gamma) + 1}\right)^{d(m+n)} \ \text{且} \ \forall \mathbf{z}_1' \in [\beta]^m, \mathbf{z}2' \in [\beta]^n, \Pr{\mathbf{y}_1, \mathbf{y}_2}[(\mathbf{z}_1, \mathbf{z}_2) = (\mathbf{z}_1', \mathbf{z}_2') \mid (\mathbf{z}_1, \mathbf{z}_2) \neq \perp] = \left(\frac{1}{2\bar{\beta} + 1}\right)^{d(m+n)} \end{gathered} $$

❝

当 $|c|_1=\eta$ ， $s \in[\beta]$ 时，我们可以简单的定义 $\gamma=\eta \cdot \beta$.

证明. 考虑$\begin{bmatrix} \mathbf{z}_1 \ \mathbf{z}_2 \end{bmatrix} = \begin{bmatrix} c\mathbf{s}_1 \ c\mathbf{s}_2 \end{bmatrix} + \begin{bmatrix} \mathbf{y}_1 \ \mathbf{y}_2 \end{bmatrix}$作为整数向量的和,用4.1.1节的记号写为

$$ \mathbf{z} = \begin{bmatrix} \mathcal{V}_{\mathbf{z}1} \ \mathcal{V}{\mathbf{z}2} \end{bmatrix} = \begin{bmatrix} \mathcal{V}{c\mathbf{s}1} \ \mathcal{V}{c\mathbf{s}2} \end{bmatrix} + \begin{bmatrix} \mathcal{V}{\mathbf{y}1} \ \mathcal{V}{\mathbf{y}_2} \end{bmatrix} \in \mathbb{Z}^{d(n+m)}. $$

$\mathbf{z}$的第$i$个系数(对于任何$i$)是$[\bar{\beta}]$中特定系数$\nuz$的概率恰好是$\frac{1}{2\bar{\beta} + 1}$。原因如下:假设$\begin{bmatrix} \mathcal{V}{c\mathbf{s}1} \ \mathcal{V}{c\mathbf{s}_2} \end{bmatrix}$中的第$i$个系数是$\nus$,那么向量$\begin{bmatrix} \mathcal{V}{\mathbf{y}1} \ \mathcal{V}{\mathbf{y}_2} \end{bmatrix}$的第$i$个系数$\nu_y$需要恰好是$\nu_z - \nu_s$。注意$\nu_z \in [\bar{\beta}]$且$\nu_s \in [\gamma]$意味着$\nu_z - \nu_s \in [\bar{\beta} + \gamma]$,这恰好是选择系数$\nu_y$的范围。因此$\nu_y$将是这个值的概率恰好是$\frac{1}{2(\bar{\beta} + \gamma) + 1}$。因此

$$ \forall \mathbf{z}_1' \in [\bar{\beta}]^m, \mathbf{z}2' \in [\bar{\beta}]^n, \Pr{\mathbf{y}_1, \mathbf{y}_2}[(\mathbf{z}_1, \mathbf{z}_2) = (\mathbf{z}_1', \mathbf{z}_2')] = \left(\frac{1}{2(\bar{\beta} + \gamma) + 1}\right)^{d(m+n)} $$

由于有$(2\bar{\beta} + 1)^{d(m+n)}$个可能的有效$(\mathbf{z}_1', \mathbf{z}_2') \in [\bar{\beta}]^m \times [\bar{\beta}]^n$可以被发送,我们得到引理第一部分的断言。

要获得引理的第二部分,我们观察到该概率= 上式/第一部分概率。□

证明者不发送$\perp$的概率是

$$ \left(\frac{2\bar{\beta} + 1}{2(\bar{\beta} + \gamma) + 1}\right)^{d(m+n)} > \left(\frac{\bar{\beta}}{\bar{\beta} + \gamma}\right)^{d(m+n)} = \left(1 + \frac{\gamma}{\bar{\beta}}\right)^{-d(m+n)} \approx e^{-\gamma d(m+n)/\bar{\beta}} $$

因此设置$\bar{\beta} = \gamma d(m+n)$会导致协议在发送非$\perp$值之前需要期望$e$次重复。当然可以将$\bar{\beta}$设置得更小,代价是更高的期望重复次数。

我们现在使用引理10来展示如何以正确的概率模拟非中止脚本,这将表明图5中的协议在不发送$\perp$的情况下是诚实验证者零知识的。

模拟器选择随机$\mathbf{z}_1 \leftarrow [\bar{\beta}]^m, \mathbf{z}_2 \leftarrow [\bar{\beta}]^n, c \leftarrow \mathcal{C}$,设置$\mathbf{w} := \mathbf{Az}_1 + \mathbf{z}_2 - c\mathbf{t}$并输出$(\mathbf{w}, c, \mathbf{z}_1, \mathbf{z}_2)$。这个分布完美模拟非中止脚本,因为$c$是均匀的,根据引理10,$\mathbf{z}_1, \mathbf{z}_2$的值是均匀随机的(对于任何$c$);而$\mathbf{w}$由其他变量唯一确定。这完成了图5中协议在不发送$\perp$时是HVZK的证明。

在继续之前,我们想指出诚实证明者发送$\perp$(从而必须重复协议)的概率 独立于 秘密$\mathbf{s}_1, \mathbf{s}_2$(引理10)。这在实际应用中很重要,因为运行时间对秘密的任何依赖都会导致侧信道攻击,其中敌手试图通过观察证明者的运行时间来推断关于秘密的一些信息。因此图5中的协议对这种特定攻击免疫。

5.2.2 知识证明

为证明该协议是PoK,使用通常的回绕（rewinding）论证(见图6),其中证明者发送$\omega$,然后成功回复两个挑战$c, c'$,分别为$(\mathbf{z}_1, \mathbf{z}_2)$和$(\mathbf{z}_1', \mathbf{z}_2')$。如果我们能提取满足验证方程的两个这样的脚本$(\mathbf{w}, c, \mathbf{z}_1, \mathbf{z}_2)$和$(\mathbf{w}, c', \mathbf{z}_1', \mathbf{z}_2')$,那么我们有$\mathbf{Az}_1 + \mathbf{z}_2 - c\mathbf{t} = \mathbf{Az}_1' + \mathbf{z}_2' - c'\mathbf{t}$。前面的式子简化为

$$ \mathbf{A}(\mathbf{z}_1 - \mathbf{z}_1') + (\mathbf{z}_2 - \mathbf{z}_2') = (c - c')\mathbf{t} $$

这恰好是所证陈述,其中$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}_2 \in [2\bar{\beta}]^n, \bar{c} \in [2]$。

公开信息: $\mathbf{A} \in \mathcal{R}{q,f}^{n \times m}, \mathbf{t} \in \mathcal{R}{q,f}^n$

图6:提取程序。

5.2.3 综合考虑

诚实验证者零知识性质意味着敌手从看到非中止脚本中不获得任何信息。知识证明性质意味着能够模拟证明者的敌手可以产生如上的解,这通过引理9意味着他可以求解环LWE或环SIS问题。两个性质一起意味着(假设环SIS和环LWE是困难的)即使敌手观察到先前的非中止有效交互,他也无法在图5的协议中模拟证明者。这使得我们可以使用Fiat-Shamir变换,在随机预言机模型中,基于环SIS和环LWE的难度构造数字签名方案。

5.2.4 参数设置

本节开头的知识证明论证意味着可以提取系数在$[2\bar{\beta}]$中的$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$和$\bar{c}$使得$|\bar{c}|1 \leq 2\eta$,满足条件。然后引理9指出如果$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$是困难的,那么上述提取意味着求解$\mathcal{R}{q,f}\text{-SIS}_{n,m+1,\bar{\beta}}$。因此最优参数设置是当这两个问题同样困难时——即这些问题在图2中的同一垂直位置。选择参数$\bar{\beta}$由引理10决定。$\bar{\beta}$应设置为约$\gamma d(m+n)$,其中$\gamma$使得对于所有$s \in [\beta]$,$cs \in [\gamma]$。因此如果选择$c$使得$|c|_1 \leq \eta$,那么$\gamma$可以设置为$\eta \cdot \beta$。因此$\bar{\beta}$比$\beta$大约$\eta d(m+n)$倍。

5.3 与离散对数方案的类比:Schnorr、Okamoto和Katz-Wang

在本节中,我们将深入探讨图5中基于格的协议与基于离散对数的协议之间的类比。

❝

本部分对于后续章节并非必需，如果只想直接阅读基于格的签名方案的最终构造，则可以跳过本部分。

如前所述,格协议及其Fiat-Shamir转换的签名方案与Schnorr识别和签名方案[Sch89]非常类似。我们将在下面看到,通过简单地改变参数$\beta$(以及从它派生的$\bar{\beta}$),可以获得具有略微不同安全特性的方案,这些方案类似于文献中其他基于离散对数的方案。最终,事实证明Schnorr实例化(可以自由设置$\beta$而没有任何约束)是最有效的变体;但我们仍然相信看到其他变体有助于更直观地了解如何构造和实例化基于格的协议是有益的。实际上,理解参数如何影响格方案的性质是设计格密码学协议的重要组成部分。

Schnorr

Schnorr协议中的公钥由随机$g$和$h = g^x$组成,其中$x$是私钥。在第一步中,证明者选择随机掩蔽变量$y$,计算$w = g^y$,并将$w$发送给验证者。验证者发送随机挑战$c$,证明者用$z = y + xc$回复,验证者检查$g^z = t^c \cdot w$。

为了证明模拟(在诚实验证者设置中)意味着破解离散对数,在收到离散对数挑战$(g, h)$后,我们将其设置为公钥。不知道使$g^x = h$的$x$,可以通过首先选择随机$z, c$,然后设置$w = g^z/t^c$来模拟诚实生成的脚本$(w, c, z)$。此后,可以证明如果敌手能够模拟,那么通常的回绕论证获得两个脚本$(w, c, z)$和$(w, c', z')$使得$g^z = t^c \cdot w$和$g^{z'} = t^{c'} \cdot w$。由此,我们得到$\bar{z} = z - z'$和$\bar{c} = c - c'$满足$g^{\bar{z}} = t^{\bar{c}}$。从后者可以得到有效的离散对数解$\bar{z}/\bar{c}$。 图5中的基于格的类比将公钥设置为$(\mathbf{A}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2)$,私钥为$\mathbf{s}_1, \mathbf{s}_2$。在格情况下,我们提取满足(74)的$\overline{\mathbf{s}}_i, \bar{c}$,然后使用引理9表明这意味着实例$[\mathbf{A} \mid \mathbf{t}]$的环SIS的解。一个小差别是在Schnorr签名的情况下,公钥$(g, g^x)$是随机的,而在格情况下,我们需要环LWE假设来论证引理9中的公钥看起来是随机的。

应该观察到,在代数上,基于格的方案和基于离散对数的方案非常相似。在两种情况下,都有某个同态单向函数族$\mathcal{F}$,公钥由$f, f(x)$组成,其中$f$是该族的随机选择成员,$x$是随机选择的私钥。第一步包括选择随机掩蔽$y$并发送$w = f(y)$。在挑战$c$上,证明者用$z = y + xc$响应。离散对数协议的不同性质是通过改变$f$的域和值域的大小之间的关系来实现的——格类比使用相同的蓝图获得,正如我们现在将看到的。

Okamoto

Okamoto协议[Oka92]在精神上与Schnorr协议相似,其主要区别特征是可以证明Okamoto识别方案对主动敌手安全——即即使验证者对抗性地选择挑战$c$,它也可以被证明是安全的。${}^{25}$由于Fiat-Shamir转换只需要HVZK,Okamoto签名的这种更强性质在实践中对于构造数字签名方案并不真正需要。

Okamoto方案中的公钥由随机$(g_1, g_2)$和$h = g_1^{x_1} \cdot g_2^{x_2}$组成。在第一步中,证明者选择随机$y_1, y_2$并输出$w = g_1^{y_1} \cdot g_2^{y_2}$。收到挑战$c$后,证明者对$i \in {1, 2}$输出$z_i = y_i + cs_i$。验证者检查$g_1^{z_1} \cdot g_2^{z_2} = h^c \cdot w$。为了证明Schnorr方案的安全性,我们需要通过首先选择随机$z, c$并从中导出$w$来模拟脚本。在Okamoto方案中,不需要模拟——所需要做的就是诚实地运行方案。从离散对数问题的归约如下进行:给定离散对数实例$(g_1, g_2)$,其中$g_2 = g_1^x$对于某个未知的$x$,提取器选择有效的私钥$x_1, x_2$并将公钥设置为$h = g_1^{x_1} \cdot g_2^{x_2}$。因此他可以通过诚实运行协议来诚实回答敌手的所有查询。如果敌手之后成功模拟证明者,那么通常的回绕论证导致两个脚本$(w, c, z_1, z_2) \neq (w, c', z_1', z_2')$使得

$$ \begin{aligned} w \cdot h^c &= g_1^{z_1} \cdot g_2^{z_2} \ w \cdot h^{c'} &= g_1^{z_1'} \cdot g_2^{z_2'} \ \end{aligned} $$

可以重写为

$$ h^{\bar{c}} = g_1^{\bar{z}_1} \cdot g_2^{\bar{z}_2} $$

其中$\bar{c} = c - c'$且$\bar{z}_i = z_i - z_i'$。通过进一步将$h$重写为$g_1^{x_1} \cdot g_2^{x_2}$,得到

$$ 1 = g_1^{\bar{z}_1 - x_1\bar{c}} \cdot g_2^{\bar{z}_2 - x_2\bar{c}} $$

现在观察到只要$\bar{z}_i - x_i\bar{c}$不都是0,我们就可以获得离散对数问题的解——即找到$x$使得$g_1^x = g_2$。

表明$\bar{z}_i - x_i\bar{c}$以很高的概率不会等于0,我们注意到给定$g_1, g_2, h = g_1^{x_1} \cdot g_2^{x_2}$,存在许多可能的$x_1', x_2'$使得$g_1^{x_1'} \cdot g_2^{x_2'} = h$——实际上,如果$g_1^x = g_2$,那么任何满足$x_1' + x \cdot x_2' = x_1 + x \cdot x_2$的$x_1', x_2'$都是有效的。这些对中的任何一个被选为原始私钥的可能性都是相等的。然后我们需要证明Okamoto协议中脚本的分布(即$w, c, z_1, z_2$)是相同的,无论选择了哪个有效私钥(即使敌手控制$c$)。

❝

这源于 $z_i$ 均匀分布，因为 $y_i$ 均匀分布，所以 $w$ 是 $z_i$ 和 $c$ 的确定性函数。

一旦确立了这一点,就可以看到如果模拟证明者的算法可以发送$\bar{z}_1, \bar{z}_2$使得$\bar{z}_i - x_i\bar{c} = 0$,那么他知道值$x_i = \bar{z}_i/\bar{c}$。但这些是信息论隐藏的,因此(即使是全能的)模拟器能够输出这样的$\bar{z}_i$的概率并不压倒性。因此模拟器可以用来求解离散对数。注意相同的证明在Schnorr协议中不起作用的原因是公钥是$(g, h = g^x)$,并且只有一个可能的私钥$x$。

在格设置中,在Schnorr型和Okamoto型方案之间移动所需要做的就是设置私钥$\mathbf{s}_1, \mathbf{s}_2$使得公钥$(\mathbf{A}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2)$以很高的概率不唯一确定私钥。这只需要我们选择更大的$\beta$。特别地,如果我们选择$\beta$使得$(2\beta + 1)^{n+m} > q^n \cdot 2^{128/d}$,那么任何(全能)算法能够恢复确切的$(\mathbf{s}_1, \mathbf{s}_2)$的概率只有$2^{-128}$。

❝

为了理解这一点，观察当给定值 $\mathbf{t}$ 时，猜测原像 ( $\mathbf{s}_1, \mathbf{s}_2$ ) 的最优策略是确定性地猜测最可能的原像。由于 $\mathbf{t}$ 的定义域大小为 $q^{n d}$，最优猜测器最多输出 $q^{n d}$ 个可能的原像。由于总共有 $(2 \beta+1)^{(n+m) d}$ 个原像，每个原像被选中的概率均等，因此最优猜测器只会输出其中 $q^{n d} /(2 \beta+1)^{(n+m) d}$ 个原像。

脚本不泄露关于$\mathbf{s}_i$的任何信息的事实在引理10中得到证明。

但就像Okamoto签名方案不如Schnorr方案高效一样,对$\beta$的附加要求将使这种基于格的实例化不太优化。我们将在介绍下一个Schnorr变体后更详细地讨论这一点。

Katz-Wang

另一个具有略微不同安全性质的Schnorr型协议是Katz-Wang协议[KW03, 第3节]。该方案的区别特征是它完全基于DDH问题,其安全性证明不需要回绕。不进行回绕的优势是安全性归约更紧。

❝

在使用回绕的归约方法中，随机预言机查询次数会损失一个倍数因子。

因此,理论上,[KW03]方案与离散对数型问题的联系更紧密。在格设置中,如果想在量子随机预言机模型(QROM)中证明方案的安全性,其中敌手被假定为量子的并且不能直接回绕(因为量子态不能被复制),那么回绕使安全性归约更不紧密。然而,无论在经典还是格设置中,从离散对数或格问题的归约的紧密性似乎都不影响签名方案的安全性,因此Okamoto和Katz-Wang方案及其格版本仍然主要只具有理论兴趣。

Katz-Wang方案中的公钥由随机$(g_1, g_2)$和$(h_1 = g_1^x, h_2 = g_2^x)$组成,对于随机秘密$x$。要签名,首先创建随机掩蔽$y$,然后计算$(w_1 = g_1^y, w_2 = g_2^y)$,并将$w_i$发送给验证者。收到挑战$c$后,证明者计算$z = y + cx$。然后验证者检查是否$g_i^z = h_i^c \cdot w_i$。

安全性归约来自DDH问题。给定DDH实例$(g_1, g_2, h_1, h_2)$,我们的任务是确定这些元素是否都是随机的,或者是否存在$x$使得$h_i = g_i^x$。

❝

这种DDH问题的表述等价于更常见的表述，即要求区分$\left(g, g^a, g^b, g^{a b}\right)$与均匀分布（只需定义$g_2=g^a$）。

给定这个$(g_1, g_2, h_1, h_2)$,我们简单地将其发布为公钥。然后可以通过首先选择$z$,然后$c$,然后导出$w_i$的值,以通常的方式创建交互的脚本。当轮到敌手模拟时,我们观察到如果$(g_1, g_2, h_1, h_2)$是随机的,那么从信息论上讲,他只有可忽略的机会成功输出有效的$z$。特别地,如果我们写$h_1 = g_1^{x_1}, h_2 = g_2^{x_2}$,对于$x_1 \neq x_2$,以及$w_1 = g_1^{r_1}, w_2 = g_2^{r_2}$,对于某些$r_i$,那么

$$ \begin{aligned} \Pr_c[\exists z \text{ s.t. } g_1^z = h_1^c \cdot w_1 \wedge g_2^z = h_2^c \cdot w_2] &= \Pr_c[\exists z \text{ s.t. } z = x_1c + r_1 \wedge z = x_2c + r_2] \ &= \Pr_c[c = (r_2 - r_1)/(x_1 - x_2)] \ &= 1/|\mathcal{C}|, \ \end{aligned} $$

其中$\mathcal{C}$是选择$c$的挑战空间的域。因此看到敌手是否能够模拟立即给我们DDH问题的解。

在来自图5协议的格方案的情况下,Katz-Wang方案的类比通过设置参数使得$\bar{\beta}$足够小以获得,使得从信息论上讲,当公钥是均匀随机$(\mathbf{A}, \mathbf{t})$时,不会存在有效响应$\mathbf{z}_1, \mathbf{z}_2$。注意在这种情况下,看到敌手是否能够成功,将允许我们区分均匀随机$(\mathbf{A}, \mathbf{t})$与$(\mathbf{A}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2)$,这恰好是环LWE问题。为了发送使验证者接受的$\mathbf{z}_1, \mathbf{z}_2$,我们需要它们在$[\bar{\beta}]$中有系数并满足$\mathbf{Az}_1 + \mathbf{z}_2 = \mathbf{tc} + \mathbf{w}$。我们想表明的是,对于所有$\mathbf{w}$,如果随机选择公钥,那么只有一个可能的挑战$c$使得存在这样的有效$\mathbf{z}_i$。

为了矛盾,假设存在两个$c, c' \in \mathcal{C}$,存在$\mathbf{z}_1, \mathbf{z}_2, \mathbf{z}_1', \mathbf{z}_2'$使得

$$ \begin{aligned} \mathbf{Az}_1 + \mathbf{z}_2 &= \mathbf{tc} + \mathbf{w} \ \mathbf{Az}_1' + \mathbf{z}_2' &= \mathbf{tc}' + \mathbf{w} \ \end{aligned} $$

结合两个方程,我们得到

$$ \mathbf{A}\overline{\mathbf{z}}_1 + \overline{\mathbf{z}}_2 = \mathbf{t}\bar{c} $$

其中$\overline{\mathbf{z}}_i = \mathbf{z}_i - \mathbf{z}_i'$且$\bar{c} = c - c'$。我们现在可以使用类似于引理2中的论证来得出结论:以很高的概率,对于随机$(\mathbf{A}, \mathbf{t})$,系数在$[2\bar{\beta}]$中的这样的$\overline{\mathbf{z}}_i$不存在。

❝

为了将该引理的类比应用于$\mathcal{R}_{q, f}$而不是$\mathbb{Z}q$，我们需要确保多项式$z \in[2 \bar{\beta}]$可逆。可以通过适当设置环$\mathcal{R}{q, f}$的参数来确保这一点（参见[LS18，推论1.2]）。

为了设置参数$\bar{\beta}$使得(84)的解以很高的概率不存在,我们需要$\bar{\beta}$略小于$q^{n/(n+m)}$(如引理2),因此$\beta$必须更小,其中两个变量之间的关系仍由引理10决定。这与Katz-Wang方案的情况一样,导致实例化不如Schnorr类比高效。

比较效率/安全性

基于格的协议的Okamoto和Katz-Wang类比对参数$\beta$和$\bar{\beta}$引入了一些约束,这些约束导致实例化不如自由选择这些值(受引理10中建立的它们之间的关系约束)时高效。在图2中,我们勾画了LWE和SIS问题的安全性如何基于参数$\beta$演变。$\text{LWE}{n,m,q,\beta}$和$\text{SIS}{n,m,q,\beta}$问题(及其多项式版本)在难度上相遇的交点大约在$q^{n/(n+m)}$。图5签名方案参数的最优设置将是$\beta$和$\bar{\beta}$在这个交点的不同侧。然而,在Okamoto型方案中,我们需要设置$\beta > q^{n/(n+m)}$以使公钥不唯一确定私钥,这使$\beta$和$\bar{\beta}$在同一侧。在Katz-Wang型方案中,我们需要$\bar{\beta} < q^{n/(n+m)}$以使用信息论论证,这又使$\beta$和$\bar{\beta}$在同一侧。我们在图7中形象地展示了这一点,这应该给出为什么方案的无约束Schnorr型变体导致最有效参数的直觉。

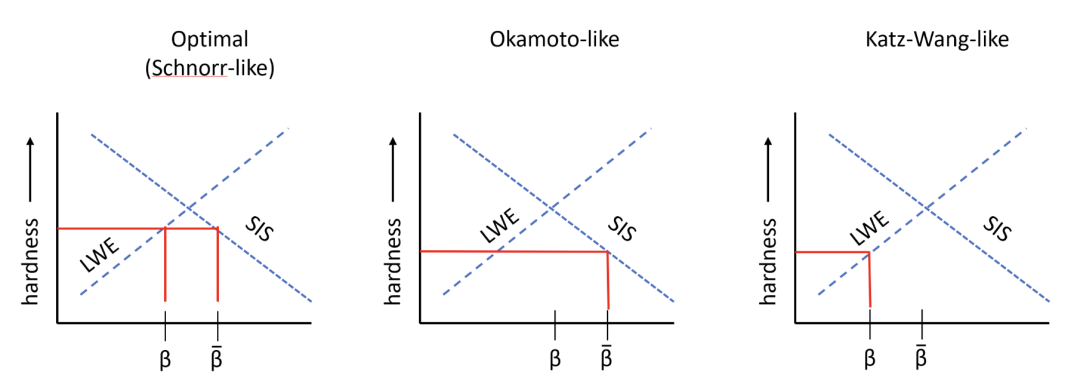
图7: 勾画图5中格协议的Schnorr、Okamoto和Katz-Wang类比的最优参数选择的直觉。Okamoto和Katz-Wang变体施加的约束导致环SIS/环LWE问题的难度较低,这将需要增加参数(如 $n$和$m$)以增加方案的安全性。

5.4 减小证明大小

在本节中,我们将展示如何通过消除证明者发送$\mathbf{z}_2$的需要来减少图5协议中证明者的通信。首先,注意在图5的交互式协议中,可以简单地从证明输出中删除$\mathbf{z}_2$,因为$\mathbf{z}_2$可以由验证者从$\mathbf{z}_1, c, \mathbf{t}$和$\mathbf{w}$重新计算为$\mathbf{z}_2 = \mathbf{w} - \mathbf{Az}_1 + c\mathbf{t}$。然而,这与如何有效使用这个交互式方案,或最终使用Fiat-Shamir变换将其转换为数字签名(见第5.6节)不兼容。在图5的协议中,实际上不需要在第一步发送向量$\mathbf{w}$,而可以发送短得多的哈希$\rho = \mathcal{H}(\mathbf{w})$,对于某个抗碰撞函数$\mathcal{H}$。验证者反过来将执行检查$\mathcal{H}(\mathbf{Az}_1 + \mathbf{z}_2 - c\mathbf{t}) = \rho$。然而,通过这种优化,不再可能像以前那样恢复$\mathbf{z}_2$,因此验证将不可能。我们真的想应用这种优化,因为不需要发送$\mathbf{w}$作为签名方案的一部分本质上使签名大小减半。因此乍一看,证明者似乎需要发送$\mathbf{w}$或$\mathbf{z}_2$。

允许我们避免发送$\mathbf{w}$和$\mathbf{z}_2$的洞察是创建$\mathbf{w}$使得验证中不需要$\mathbf{z}_2$。因为图5中验证过程中的$\mathbf{z}_2$以良好的概率不影响$\mathbf{w}$的高阶位,我们可以发送只包含$\mathbf{Ay}_1 + \mathbf{y}_2$的高阶位的$\mathbf{w}$。此外,由于$\mathbf{y}_2$也以良好的概率不影响高阶位,我们可以将$\mathbf{w}$定义为$\mathbf{Ay}_1$的高阶位,然后让验证者检查$\mathbf{Az}_1 - c\mathbf{t}$的高阶位是否为$\mathbf{w}$。如果这有效,那么等式$\mathcal{H}(\mathbf{Az}_1 - c\mathbf{t}) = \mathcal{H}(\mathbf{w})$也成立,因此证明者可以发送$\rho = \mathcal{H}(\mathbf{w})$而不是$\mathbf{w}$,我们因此消除了发送$\mathbf{z}_2$或$\mathbf{w}$的需要!

通过不发送$\mathbf{z}_2$,乍一看,协议似乎消除了对秘密$\mathbf{s}_2$的依赖,人们可能希望我们甚至最终可能具有较低的协议中止概率,因为不再有向量$\mathbf{z}_2$需要检查。然而,这并不完全正确——证明者仍然需要使用$\mathbf{s}_2$以使协议保持零知识。

不发送$\mathbf{z}_2$的想法和执行在精神上与第2.5.1节中缩短密文的位丢弃想法有些相似。签名协议中不发送$\mathbf{z}_2$的想法出现在[GLP12, BG14]中,我们在图8中呈现的协议归功于[BG14]。如第2.5.1节,假设我们选择大小为$2^\kappa$的集合$\mathcal{S} \subset \mathbb{Z}_q$,使得该集合中任何两个元素之间的距离$\approx q/2^\kappa$。让我们也回忆该节中的记号,可以唯一地将任何$w \in \mathbb{Z}_q$表示为$w = \text{HIGH}_S(w) + \text{LOW}_S(w)$,其中$\text{HIGH}_s(w) \in S$且$\text{LOW}_S(w) = w - \text{HIGH}S(w) \in [q/2^{\kappa+1}]$。这个记号可以自然地扩展到$\mathcal{R}{q,f}$上的向量,通过对每个多项式的每个整数系数应用此分解。

此外,定义$\delta_S$为最大整数使得对于所有$2^\kappa$个元素$s_i \in \mathcal{S}$,集合$s_i + [\delta_S]$都是不相交的。如果我们选择$\mathcal{S}$中的点使它们在表示$\mathbb{Z}_q$的圆上彼此等距(距离变化至多1,因为$q$可能不能被$2^\kappa$整除),那么$\delta_S$将约为$q/2^{\kappa+1}$,这也是(再次,在1以内)对所有$w \in \mathbb{Z}_q$,$\text{LOW}_S(w)$的最大值。在本节的其余部分,我们将假设$\mathcal{S}$以这种方式选择。一个重要的简单观察是,对于所有正$\gamma < \delta_S$和$s \in [\gamma]$,

$$ \text{LOW}_S(w) \in [\delta_S - \gamma] \Longrightarrow \text{HIGH}_S(w) = \text{HIGH}_S(w + s) $$

使用上述记号,考虑图8中的协议。我们将表明它是满足要求的$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}_2 \in [q/2^\kappa]^n, \bar{c} \in \overline{\mathcal{C}}$的知识证明。

私有信息: $\mathbf{s}_1 \in [\beta]^m, \mathbf{s}2 \in [\beta]^n$公开信息: $\mathbf{A} \in \mathcal{R}{q,f}^{n \times m}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}2 \in \mathcal{R}{q,f}^n$

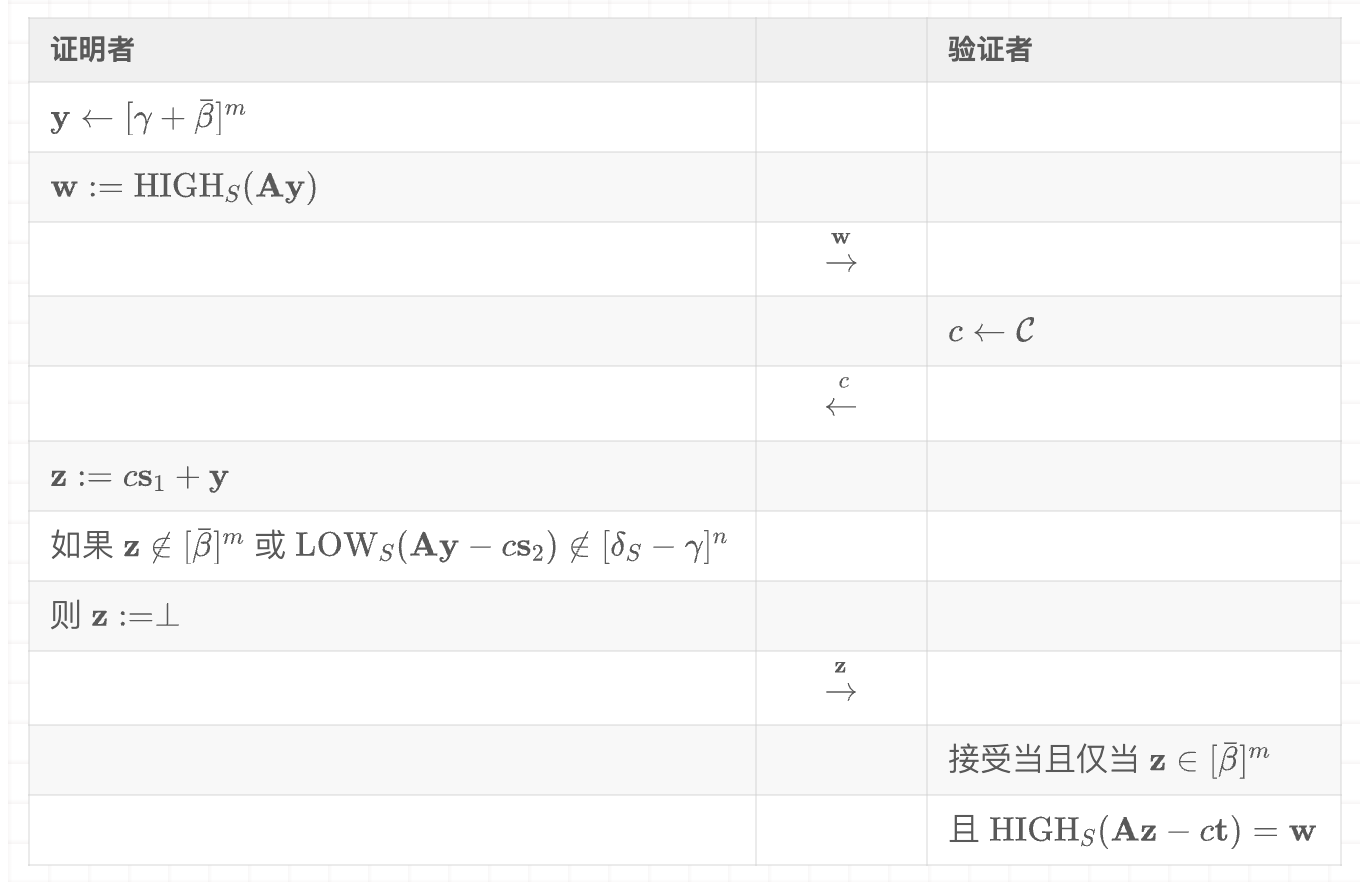
_图8: 具有较小输出的基本零知识证明系统。集合$\mathcal{S} \in \mathbb{Z}_q$的大小为$2^\kappa$,函数$\text{HIGH}_S, \text{LOW}_S$和常数$\delta_S$如第5.4节文本中定义。证明者知道满足(73)的$\mathbf{s}_1 \in [\beta]^m, \mathbf{s}_2 \in [\beta]^n$,产生满足要求的$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}2 \in [q/2^\kappa]^n$和$\bar{c} \in \overline{\mathcal{C}}$的ZKPoK。值$\gamma$在引理10中定义,$\beta$的值影响协议的完备性(即不发送$\perp$的概率)

5.4.1 正确性

对于正确性(在$\mathbf{z} \neq \perp$的情况下),我们需要证明$\text{HIGH}_S(\mathbf{Ay}) = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。如果写

$$ \mathbf{Az} - c\mathbf{t} = \mathbf{A}(c\mathbf{s}_1 + \mathbf{y}) - c(\mathbf{As}_1 + \mathbf{s}_2) = \mathbf{Ay} - c\mathbf{s}_2 $$

通过证明者不发送$\perp$的条件之一知道$\text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2) \in [\delta_S - \gamma]^n$。后者通过观察意味着$\text{HIGH}_S(\mathbf{Ay}) = \text{HIGH}_S(\mathbf{Ay} - c\mathbf{s}_2)$,因此$\mathbf{w} = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。

5.4.2 零知识

如前所述,我们将只展示如何模拟不发送$\perp$的脚本。从引理10,知道在$\mathbf{z} \in [\bar{\beta}]^m$的条件下,它是均匀随机的。因此我们的模拟在$[\beta]^m$中选择均匀随机的$\mathbf{z}$和$c \in \mathcal{C}$。然后他检查是否$\text{LOW}_S(\mathbf{Az} - c\mathbf{t}) \in [\delta_S - \gamma]^n$。如果不是,则重新采样$\mathbf{z}$和$c$并再次尝试。一旦成功,他设置$\mathbf{w} := \text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$并输出视图$(\mathbf{w}, c, \mathbf{z})$。因为第一次检查通过后$\mathbf{z}$具有正确的分布,并且第二次检查在真实证明和模拟中完全相同,所以模拟完美模拟非中止脚本。

在上述模拟中,至关重要 的是模拟器能够完美模拟真实证明者的检查:

$$ \text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2) \in [\delta_S - \gamma]^n. $$

这就是为什么在真实证明中执行这个检查而不是不同的可能限制性较小的检查的原因。不需要上式成立以使验证方程得到满足。如果证明者直接检查验证者将接受——即简单地检查$\mathbf{w} = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$,方案仍然是完备的。但模拟器不能执行此检查,因为他不知道$\mathbf{w}$($\mathbf{w}$在模拟中在设置$\mathbf{z}$并检查上式之后设置),因此方案将失去其ZK性质。因此上式中的检查是必要的,以同时确保正确性和可模拟性(从而安全性)。

5.4.3 计算$\perp$的概率

类似于引理10中的计算,我们知道$\Pr_{\mathbf{y}}[\mathbf{z} \in [\bar{\beta}]^m] = \left(\frac{2\bar{\beta} + 1}{2(\bar{\beta} + \gamma) + 1}\right)^{dm} \approx e^{-\gamma dm/\bar{\beta}}$。要计算$\text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2) \in [\delta_S - \gamma]^n$的概率,我们做启发式假设$\mathbf{Ay} - c\mathbf{s}2$的分布在$\mathcal{R}{q,f}^n$中是均匀的,因此$\text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2)$在$[\delta_S]^n$中均匀分布。因此$[\delta_S]^n$中随机元素在$[\delta_S - \gamma]^n$内的概率是

$$ \left(\frac{2(\delta_S - \gamma) + 1}{2\delta_S + 1}\right)^{dn} > \left(1 - \frac{\gamma}{\delta_S}\right)^{dn} \approx e^{-\gamma dn/\delta_S} $$

结合两个概率,我们得到

$$ \Pr_{\mathbf{y}}[\mathbf{z} \neq \perp] \approx e^{-\gamma d(m/\bar{\beta} + n/\delta_S)} $$注意较大的$\bar{\beta}$和较大的$\delta_S$增加协议的正确性概率。但正如我们将在下面看到的,这些值越大,提取的满足(74)的$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$中的系数就越大。

我们指出,即使我们做启发式假设来计算$\text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2) \in [\delta_S - \gamma]^n$的概率,不需要使用任何启发式来论证输出$\perp$的概率独立于私钥(这是防止侧信道攻击所需的)。这是因为$\mathbf{z}$的分布独立于私钥(引理10),并且$\text{LOW}_S(\mathbf{Ay} - c\mathbf{s}_2) = \text{LOW}_S(\mathbf{Az} - c\mathbf{t})$,因此这也独立于私钥。

5.4.4 知识证明

通过回绕,提取器可以获得满足验证方程的两个脚本$(\mathbf{w}, c, \mathbf{z})$和$(\mathbf{w}, c', \mathbf{z}')$,因此$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t}) = \text{HIGH}_S(\mathbf{Az}' - c'\mathbf{t})$。根据定义,我们有

$$ \begin{aligned} \mathbf{Az} - c\mathbf{t} &= \text{HIGH}_S(\mathbf{Az} - c\mathbf{t}) + \text{LOW}_S(\mathbf{Az} - c\mathbf{t}) \ \mathbf{Az}' - c'\mathbf{t} &= \text{HIGH}_S(\mathbf{Az}' - c'\mathbf{t}) + \text{LOW}_S(\mathbf{Az}' - c'\mathbf{t}) \end{aligned} $$

其中$\text{LOW}_S(\mathbf{Az} - c\mathbf{t}), \text{LOW}_S(\mathbf{Az} - c\mathbf{t}) \in [q/2^{\kappa+1}]^n \approx [\delta_S]^n$。减去上述两个方程,我们得到

$$ \mathbf{A}(\mathbf{z} - \mathbf{z}') - (c - c')\mathbf{t} = \text{LOW}_S(\mathbf{Az} - c\mathbf{t}) - \text{LOW}_S(\mathbf{Az}' - c'\mathbf{t}) \in [q/2^\kappa]^n \approx [2\delta_S]^n $$

当我们将$\overline{\mathbf{s}}_2$设置为$\text{LOW}_S(\mathbf{Az} - c\mathbf{t}) - \text{LOW}_S(\mathbf{Az}' - c'\mathbf{t})$时,这等价于前式。

5.5 减小公钥大小

我们现在继续通过展示如何减小公钥大小来提高签名方案的效率。类似于上一节中由于$\mathbf{Az}_1 \approx c\mathbf{t}$的事实而从图5的协议中消除传输$\mathbf{z}2$需要的直觉,我们还注意到如果我们写$\mathbf{t} = \text{HIGH}{\mathcal{T}}(\mathbf{t}) + \text{LOW}_{\mathcal{T}}(\mathbf{t})$(其中$\mathcal{T} \subset \mathbb{Z}_q$),那么$\mathbf{Az}_1 \approx c \cdot (\text{HIGH}_T(\mathbf{t}) + \text{LOW}_T(\mathbf{t})) \approx c \cdot \text{HIGH}_T(\mathbf{t})$。换句话说,验证者不需要知道$\mathbf{t}$的低阶位就能近似验证验证方程。

通过不使$\text{LOW}{\mathcal{T}}(\mathbf{t})$成为公钥的一部分,我们再次遇到与上一节类似的问题,即如果不对协议进行一些调整,验证者将想要仅知道$\text{HIGH}{\mathcal{T}}(\mathbf{t})$而不是整个$\mathbf{t}$的情况下计算$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。我们现在将描述使证明工作所需的技术,并在图9中呈现来自[DKL+18]的协议。

类似于我们在上一节中定义集合$S \subset \mathbb{Z}_q$的方式,我们定义集合$\mathcal{T} \subset \mathbb{Z}q$,它由$2^\ell$个元素组成,每个元素相距约$q/2^\ell$。我们不将整个向量$\mathbf{t} \in \mathcal{R}{q,f}^n$作为公钥的一部分输出,而是将其分解为$\mathbf{t} = \mathbf{t}_1 + \mathbf{t}_0$,其中$\mathbf{t}1 = \text{HIGH}{\mathcal{T}}(\mathbf{t})$且$\mathbf{t}0 = \text{LOW}{\mathcal{T}}(\mathbf{t})$。公钥将只包含$\mathbf{t}_1$,它需要$nd\ell$比特来表示,而不是表示整个$\mathbf{t}$所需的$nd\log q$比特。

验证者在图8协议中使用$\mathbf{t}$的地方是计算$\mathbf{Az} - c\mathbf{t}$。如果验证者只有$\mathbf{t}_1$,那么他可以计算$\mathbf{Az} - c\mathbf{t}_1 = \mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0$。为了使验证成功,我们需要

$$ \text{HIGH}_S(\mathbf{Az} - c\mathbf{t}) = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t}_1) $$

或者换句话说,

$$ \text{HIGH}_S(\mathbf{Az} - c\mathbf{t}) = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0). $$

此时,自然的问题是为什么不通过应用与上一节相同的技术来解决这个问题?即,我们可以确保对于某个$\gamma'$,$c\mathbf{t}_0 < \gamma'$,然后使用前述的观察来强制上述方程总是成立。这种方法的问题是它是浪费的,不太可能导致大小的有用减少。我们将$c\mathbf{s}_2$的系数(对于所有可能的秘密$\mathbf{s}_2$)上界为$\gamma$的原因是我们需要保持$\mathbf{s}_2$为秘密。另一方面,我们不需要保持$\mathbf{t}_0$为秘密——我们只是希望它对验证来说是不必要的。因此如果验证者能够计算依赖于$\mathbf{t}_0$的东西——即$\mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0$,这完全没问题。我们这里的唯一目标是确保知道$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0)$的验证者能够导出$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。

主要观察是,如果$c\mathbf{t}_0 \in [\delta_S]^n$,那么可以计算$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0)$的验证者只需要一比特的额外信息(每个系数)来确定$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。特别地,如果某个整数点$v$在表示$\mathbb{Z}_q$的圆上集合$\mathcal{S}$中的点$si$和$s{i+1}$之间,我们向其添加$[\delta_S]$中的整数点$v'$,那么$v + v'$的最接近点在$S$中只能是$si$或$s{i+1}$(即$\text{HIGH}_S(v + v') = si$或$s{i+1}$)。知道$v$和$v'$的证明者可以向验证者提供这一比特的信息。换句话说,他可以告诉验证者$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t}) = \text{HIGH}_S(\mathbf{Az} - c\mathbf{t} + c\mathbf{t}_0)$是否成立。无论哪种方式,验证者现在都可以确定$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$。使用这种技术,可以以向签名添加额外$dn$"提示"比特为代价显著减小公钥大小。

作为记号,我们将写$\text{HINT}(\mathbf{Az} - c\mathbf{t}_1, c\mathbf{t}_0) = \mathbf{h} \in {0, 1}^{dn}$作为从$\mathbf{Az} - c\mathbf{t}_1$恢复$\text{HIGH}_S(\mathbf{Az} - c\mathbf{t})$所需的提示向量。我们将写$\text{USEHINT}(\mathbf{Az} - c\mathbf{t}_1, \mathbf{h})$作为这个恢复过程。特别地,$\text{USEHINT}(\mathbf{Az} - c\mathbf{t}_1, \mathbf{h})$计算$\mathbf{v} = \mathbf{Az} - c\mathbf{t}_1$,然后对于$\mathbf{v}$的每个整数系数(它位于$\mathcal{S}$中的$si$和$s{i+1}$之间),它使用$\mathbf{h}$的相应比特来输出较近的$s_i$(如果提示比特是0)或较远的那个(如果提示比特是1)。在实践中,通常情况下大多数时候提示比特将是0,因此提示向量可以通过仅枚举提示比特为1的位置来更有效地表示。

❝

事实上，当 $ct_0 \in [2\delta_S - 1]$ 而非 $[\delta_S]$ 时，有一种方法可以计算一个 1 比特的提示。观察发现，对于任何点 $v \in \mathbb{Z}_q$，集合 $v + [2\delta_S - 1]$ 最多包含来自 $S$ 的 2 个点，因此这个提示可以用来指引我们找到正确的点。这一点由 Jonathan Katz 和 [BDL24] 的研究独立发现。

这一发现使我们能够进一步压缩公钥，因为现在 $t_0$ 的范数基本上可以大一倍（即其系数可以大一个比特），而代价只是略微增加了签名的大小，因为新的提示向量现在是均匀随机的，而不是稀疏的。一些可能的权衡在 [BDL24, 表 1] 中给出。这个发现是在 ML-DSA 已经成为标准之后才提出的，因此未能被考虑纳入其中。

私有信息: $\mathbf{s}_1 \in [\beta]^m, \mathbf{s}2 \in [\beta]^n$ 公开信息: $\mathbf{A} \in \mathcal{R}{q,f}^{n \times m}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2$(验证者不使用), $\mathbf{t}1 = \text{HIGH}{\mathcal{T}}(\mathbf{t})$

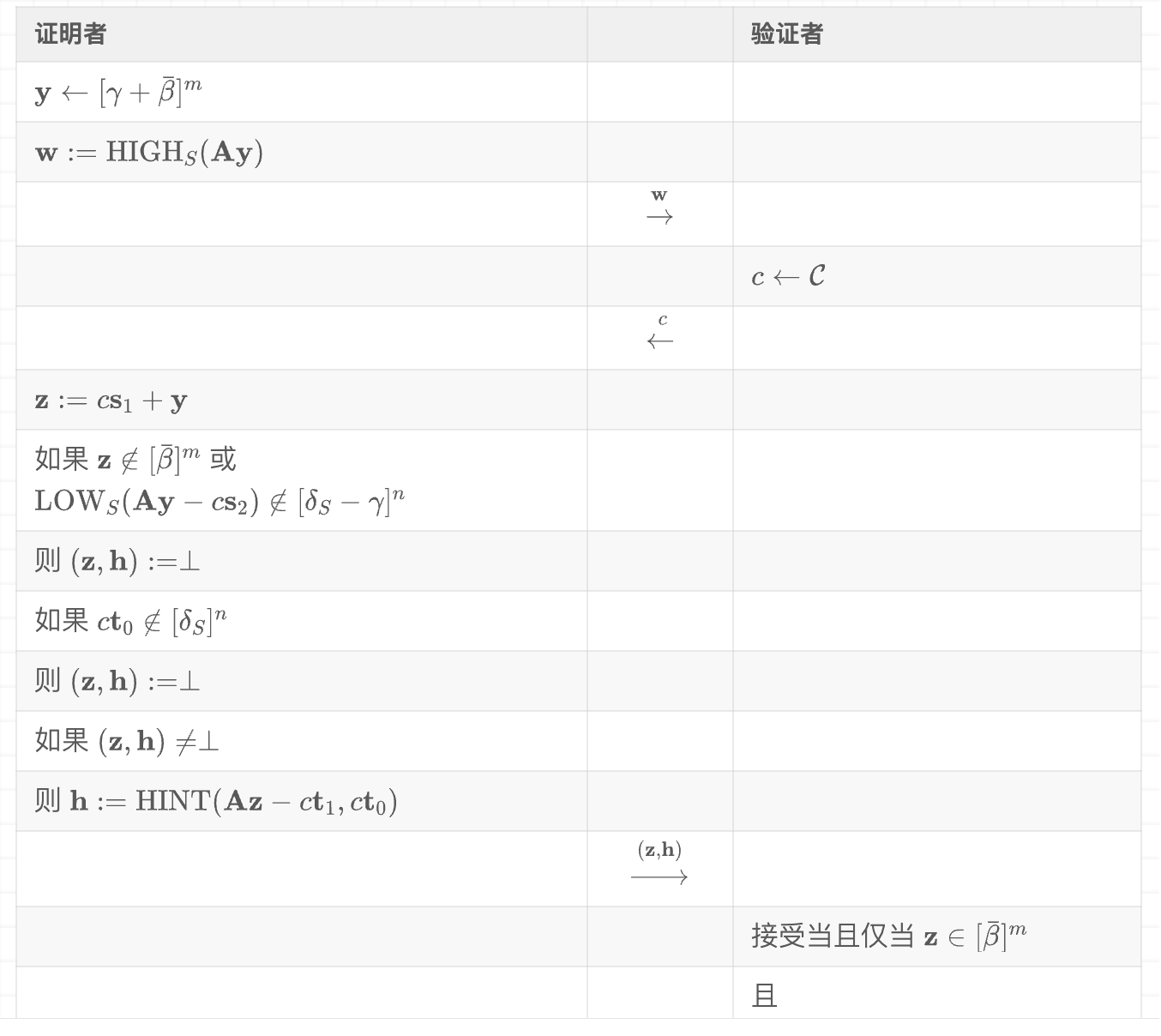
_图9: 具有较小证明和较小公钥的零知识证明系统。集合$\mathcal{S} \in \mathbb{Z}_q$的大小为$2^\kappa$,函数$\text{HIGH}_S, \text{LOW}_S$和常数$\delta_S \approx q/2^{\kappa+1}$如第5.4节文本中定义。集合$\mathcal{T}$的大小为$2^\ell$,我们要求以很高的概率(对于$c$和$\mathbf{t}$的选择),$c \cdot \text{LOW}_T(\mathbf{t}) \in [\delta_S]^n$。函数HINT和USEHINT如第5.5节文本中定义。证明者知道$\mathbf{s}_1 \in [\beta]^m, \mathbf{s}_2 \in [\beta]^n$,产生$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}2 \in [q/2^{\kappa-1}]^n$和$\bar{c} \in \overline{\mathcal{C}}$的ZKPoK。值$\gamma$在引理10中定义,$\bar{\beta}$的值影响协议的完备性(即不发送$\perp$的概率)。

使用这个记号,对于任何向量$\mathbf{v} \in \mathcal{R}_{q,f}^n$和提示向量$\mathbf{h} \in {0, 1}^{dn}$,注意到

$$ \mathbf{v} - \text{USEHINT}(\mathbf{v}, \mathbf{h}) \in [q/2^\kappa]^n \approx [2\delta_S]^n $$

对于安全性证明很重要。上述直接从USEHINT过程和$\mathcal{S}$中两个相邻点之间的距离为$q/2^\kappa$的事实得出。

图9中协议证明的陈述是$\overline{\mathbf{s}}_1 \in [2\bar{\beta}]^m, \overline{\mathbf{s}}_2 \in [q/2^{\kappa-1}]^n$和$\bar{c} \in \overline{\mathcal{C}}$的知识,满足

$$ \mathbf{A}\overline{\mathbf{s}}_1 + \overline{\mathbf{s}}_2 = \bar{c}\mathbf{t}_1 $$

如果我们想将其与原始$\mathbf{t}$联系起来,我们可以代入$\mathbf{t}_1 = \mathbf{t} - \mathbf{t}_0$并将上述方程重写为$\mathbf{A}\overline{\mathbf{s}}_1 + (\overline{\mathbf{s}}_2 + \bar{c}\mathbf{t}_0) = \bar{c}\mathbf{t}$,因此向量$\overline{\mathbf{s}}_2$的长度增加了所有$\bar{c} \in \overline{\mathcal{C}}$中$\bar{c}\mathbf{t}_0$的最大可能值。

5.5.1 正确性和零知识

值得重复的一个重要点是,虽然验证者不需要$\mathbf{t}0 = \text{LOW}{\mathcal{T}}(\mathbf{t})$的值进行验证,但不应将值$\mathbf{t}_0$视为秘密,因为输出$\mathbf{h}$会泄露关于$\mathbf{t}_0$的一些信息。对于证明来说,思考$\mathbf{t}$的方式是验证者知道整个$\mathbf{t}$,但只在验证中使用$\mathbf{t}_1$。该方案的零知识性质立即从图8中方案的零知识性质得出,我们已经在第5.4.2节中建立了这一点,因为证明者输出中的唯一区别是提示$\mathbf{h}$的构造,这可以通过知道$\mathbf{z}$和$\mathbf{t}$来完成。

每当$c\mathbf{t}_0 \in [\delta_S]^n$时,方案的正确性就会成立。注意如果$\mathbf{t}_0$被选择使得$c\mathbf{t}_0$有时不在$[\delta_S]^n$中,这不会影响方案的安全性——尽管这将需要证明者进行额外的重启。

5.5.2 知识证明

通过回绕,获得脚本$(\mathbf{w}, c, (\mathbf{z}, \mathbf{h}))$和$(\mathbf{w}, c', (\mathbf{z}', \mathbf{h}'))$,因此我们有

$$ \text{USEHINT}(\mathbf{Az} - c\mathbf{t}_1, \mathbf{h}) = \text{USEHINT}(\mathbf{Az}' - c'\mathbf{t}_1, \mathbf{h}'). $$

且

$$ \begin{aligned} \mathbf{Az} - c\mathbf{t}_1 - \text{USEHINT}(\mathbf{Az} - c\mathbf{t}_1, \mathbf{h}) &\in [q/2^\kappa]^n \ \mathbf{Az}' - c'\mathbf{t}_1 - \text{USEHINT}(\mathbf{Az}' - c'\mathbf{t}_1, \mathbf{h}') &\in [q/2^\kappa]^n \end{aligned} $$

这与上式一起意味着

$$ \mathbf{A}(\mathbf{z} - \mathbf{z}') - (c - c')\mathbf{t}_1 \in [q/2^{\kappa-1}]^n \approx [4\delta_S]^n $$

这反过来直接意味着$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$和$\bar{c}$的知识。

5.6 数字签名

图10中的签名过程是图9协议的Fiat-Shamir变换,其中私钥$\mathbf{s}_1, \mathbf{s}_2$从各自的域均匀随机选择。一个重要的点,我们之前提到过,是因为协议不再是交互式的,证明者永远不需要发送$\perp$——他可以简单地继续重启协议,直到拒绝采样步骤成功。这就是为什么我们只需要在不输出$\perp$的情况下证明零知识性质的原因。

协议的正确性和可模拟性/零知识性质直接从图9交互式协议的相应性质和随机预言机启发得出。通过Fiat-Shamir变换的通用性质,我们知道可以从成功的签名者中提取与第5.5.2节中成功的证明者相同的东西——$\overline{\mathbf{s}}_1, \overline{\mathbf{s}}_2$和$\bar{c}$。然后应用引理9意味着提取这些值与环LWE或环SIS一样困难。

私有信息: $\mathbf{s}_1 \leftarrow [\beta]^m, \mathbf{s}2 \leftarrow [\beta]^n$ 公开信息: $\mathbf{A} \in \mathcal{R}{q,f}^{n \times m}, \mathbf{t} = \mathbf{As}_1 + \mathbf{s}_2$(验证者不使用), $\mathbf{t}1 = \text{HIGH}{\mathcal{T}}(\mathbf{t})$

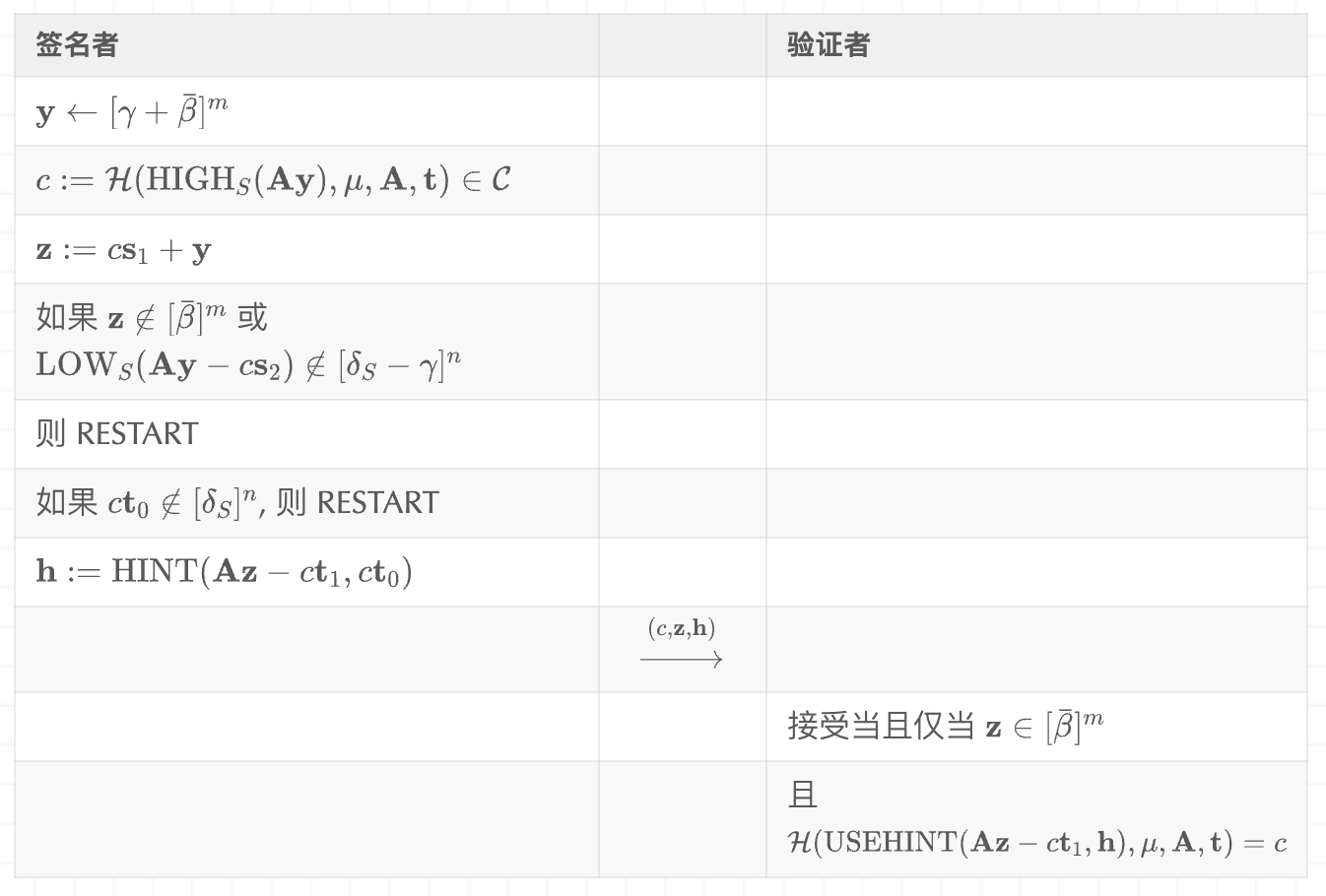
图10: 通过对图9中协议应用Fiat-Shamir变换获得的数字签名方案,签署消息(摘要)$\mu$。注意作为良好的密码学实践,我们将公钥作为哈希函数$\mathcal{H}$的输入。这防止了一些延展性攻击,其中看到一个公钥的签名允许为另一个密切相关的公钥创建签名。

5.7 签名方案CRYSTALS-Dilithium(ML-DSA)

我们现在给出一个数字签名方案的示例实例化,与[DKL+18]非常相似,(保守地)估计具有192比特的安全性。

我们将在环$\mathcal{R}_{q,f}$上工作,其中$f = X^{256} + 1$且$q = 2^{23} - 2^{13} + 1$。素数$q$的这种选择允许高效的NTT,因为$q \equiv 1 \pmod{512}$,如第4.6节所述。挑战集$\mathcal{C}$由系数为$0, \pm 1$的多项式组成,恰好有$207$个$0$(因此有$49$个非零),秘密$\mathbf{s}_1, \mathbf{s}_2$的系数从$[\beta]$随机选择,其中$\beta = 4$。

然后集合$\mathcal{S}$和$\mathcal{T}$如表4中定义。集合$\mathcal{S}$的定义意味着$\mathbb{Z}_q$中的每个点距$\mathcal{S}$中的任何元素最多$(q-1)/32 + 1$。类似地,$\mathcal{T}$的定义意味着$\mathbf{t}_0$的所有系数都在$[2^{12}]$中。现在可以检查$c\mathbf{t}0$以很高的概率在$[\delta{\mathcal{S}}]$中有系数,因此方案将是正确的(以很高的概率)。为了使方案总是正确,证明者应该额外检查$c\mathbf{t}0 \in [\delta{\mathcal{S}}]^6$,我们设置参数使其以非常小的概率($< 1%$)发生。${}^{32}$

不发生重启的概率从(89)计算为约

$$ e^{-196 \cdot 256 \cdot (5/2^{19} + 6 \cdot 32/(q-1))} \approx 0.2, $$

这意味着在产生签名之前平均需要约5次签名尝试。这使得签名过程明显慢于验证。尽管如此,签名过程的优化实现在标准个人计算机上运行时间远低于一毫秒。

公钥由用于扩展公共矩阵$\mathbf{A}$的256比特种子$\rho$和向量$\mathbf{t}1 = \text{HIGH}{\mathcal{T}}(\mathbf{As}_1 + \mathbf{s}_2)$组成。由于集合$\mathcal{S}$可以用10比特描述,并且$\mathbf{t}_1$中有$6 \cdot 256$个整数元素,$\mathbf{t}_1$的描述需要$6 \cdot 256 \cdot 10$比特。因此公钥由1952字节组成。

表4: 与NIST Level 3参数集(即应该与AES-192一样困难的参数集)非常相似的数字签名方案的示例参数CRYSTALS-Dilithium [DKL+18]。

参数	值
$q$	$2^{23} - 2^{13} + 1$
$f(X)$	$X^{256} + 1$
$\beta$	4
$(n, m)$	$(6, 5)$
$\mathcal{C}$	$c \in [-1, 1]$,有$49$个$\pm 1$和$207$个$0$
$\gamma$	$49 \times 4 = 196$
$\bar{\beta}$	$2^{19} - \gamma - 1$
$\mathcal{S}$	${i \cdot (q-1)/16 \mid 0 \leq i \leq 15}$
$\delta_{\mathcal{S}}$	$(q-1)/32 - 1$
$\mathcal{T}$	${i \cdot 2^{13} \mid 0 \leq i \leq (q-1)/2^{13}}$

签名由向量$\mathbf{z}_1$、挑战$c$和提示向量$\mathbf{h}$组成。由于$\mathbf{z}_1$的系数在$[\beta]$中,其表示每个系数需要20比特,总共$256 \cdot 5 \cdot 20$比特。挑战$c$由大约256比特组成,而提示向量$\mathbf{h}$是维度为$256 \cdot 6$的二进制向量,因此最多需要那么多比特来表示。因此总签名大小约为3424字节。

一些优化

我们现在讨论图10中协议的一些小优化,这些优化用于ML-DSA(Dilithium)NIST标准中。如果消息$\mu$非常长,那么每次重启后计算$\mathcal{H}(\text{HIGH}_S(\mathbf{Ay}), \mu, \mathbf{A}, \mathbf{t})$将不必要地低效。因此,首先使用SHA-512对真实消息$\mu'$进行哈希以获得512比特摘要$\mu$,连同公钥,并仅在签名过程中使用此摘要是有意义的。

为了使$\mathbf{y}$的采样尽可能高效(因为它也在每次重启时被采样一次),可以使每个系数被采样的范围为2的幂,因此恰好20比特。因此不是从$[\gamma + \bar{\beta}] = [2^{19} - 1]$采样,其中每个系数来自大小为$2^{20} - 1$的域,我们将从集合${-(2^{19} - 1), \ldots, 2^{19} - 1, 2^{19}}$采样每个系数。

上面提到的另一个优化是发送提示向量$\mathbf{h}$的紧凑表示。以很高的概率,对于表4中的参数,向量$\mathbf{h}$将最多有55个1,因此$256 \cdot 6 - 55$个0。不是发送$256 \cdot 6$比特字符串,而是可以指定多项式内0的位置(每个非零系数需要8比特,所以8.55比特),还指定多项式之间的边界,这需要$5 \cdot 6 = 30$比特,总共470比特而不是朴素的$256 \cdot 8 = 1536$,这将签名大小减少到约3290字节。这将要求签名者在$\mathbf{h}$中非零条目的数量大于55时执行重启,但从实验来看,这以非常小的概率发生,不会显著影响运行时间。

安全性

如前所述,签名方案的安全性依赖于$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$和$\mathcal{R}{q,f}\text{-SIS}{n,m+1,2\bar{\beta}}$问题的难度。$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$假设用于证明公钥$(\mathbf{A}, \mathbf{t})$与均匀分布不可区分,$\mathcal{R}{q,f}\text{-SIS}{n,m+1,2\bar{\beta}}$假设用于表明敌手不能伪造签名,因此找不到$\mathcal{R}{q,f}\text{-SIS}{n,m+1,2\bar{\beta}}$问题的解,其中$\overline{\mathbf{s}}_1$的系数在$[2\bar{\beta}]$中,$\overline{\mathbf{s}}2$的系数在$[4\delta{\mathcal{S}}]$中,对于表4中的参数,两个集合都约为$[2^{20}]$。因此这对应于表2中参数集的中间行,可以看到控制问题难度的$\delta$值对于$\mathcal{R}{q,f}\text{-LWE}{n,m,\beta}$和$\mathcal{R}{q,f}\text{-SIS}{n,m+1,2\bar{\beta}}$来说大致相似。

（全文完）

❝

Kurt Pan: 如您喜歡，請打賞支持我！👇

讓我們一起向 付費圍牆花園 和 廣告推薦注意力經濟 宣戰，讓賽博空間重新清朗！

• 本文转载自： mp.weixin.qq.com/s/H1FKE... , 如有侵权请联系管理员删除。