AUCIL:一种基于拍卖的包含列表设计,用于增强以太坊权益证明的审查抗性 - 权益证明/区块提议者
- 以太坊中文
- 发布于 2024-09-13 10:17
- 阅读 1130
本文介绍了一种基于拍卖的包含列表设计(AUCIL),该设计利用了由理性参与者组成的包含列表委员会中的竞争。该协议设计利用了两个关键组件:(i) 输入列表创建机制,允许委员会成员选择非重叠的交易,同时最大化他们的费用;(ii) 拍卖机制,允许各方确保大多数这些输入列表都包含在最终输出包含列表中。前者确保考虑包含许多被审查的交易,而后者采用竞争,激励尽可能多地包含输入列表以生成输出包含列表。
由 @sarisht @kartik1507 @voidp @soispoke @Julian
与 @barnabe @luca_zanolini @fradamt 合作 - 2024年9月12日
TLDR;
在本文中,我们介绍了一种基于拍卖的包含列表设计,AUCIL,它利用了由理性方组成的包含列表委员会内部的竞争。该协议设计利用了两个关键组成部分:(i)一种输入列表创建机制,允许委员会成员选择非重叠的交易,同时最大化他们的费用,以及(ii)一种拍卖机制,允许各方确保这些输入列表中的大多数都包含在最终的输出包含列表中。前者确保了许多被审查的交易被考虑包含,后者采用了竞争,其中鼓励包含尽可能多的输入列表以生成输出包含列表。
介绍
如今,以太坊的中心化构建者生态系统已经导致大约 2 个构建者有权决定哪些交易发布在以太坊上。这种中心化导致了审查问题,因为构建者对包含哪些交易拥有完全的权力。以太坊当前提出(并拒绝)的解决方案(EIP 7547)要求当前的提议者确定要由下一个提议者包含的包含列表(或被审查交易的集合)。这样的提议者也充当了单点故障,很容易被贿赂以排除交易。这导致了诸如 COMIS 和 FOCIL 等提议,这些提议需要来自多个提议者的输入进行聚合以形成包含列表。
直观地说,使用多个提议者意味着需要贿赂多个方才能排除交易。但是,所有方是否首先都包含该交易?由于生成的包含列表是有限的(受区块大小限制),这些方中的每一方如何决定在其本地列表中包含哪些交易,使得最大化效用也能提高系统的吞吐量? 此外,在聚合交易以生成包含列表时,有多少个故障点可以被贿赂以排除交易?本文介绍了一种名为 AUCIL 的多提议者设计,旨在解决这些问题。
动机
让我们首先说明应如何创建包含列表的第一部分。对于现有的包含列表设计,复杂的假设是 IL 提议者可以包含它看到的尽可能多的交易。虽然 FOCIL 或 COMIS 对本地包含列表中的交易提议没有明确规定,但 Fox et al. 假设不存在网络拥塞。但是,包含所有交易可能会导致包含列表的大小大于区块大小的情况。在这种情况下,构建者(受到包含列表中交易的约束)将添加尽可能多的交易,并删除包含列表中剩余的任何交易。
上面首先要注意的是,对于 IL 提议者来说,添加比区块大小更多的交易是没有意义的,因此,对本地包含列表可能存在一个隐式的区块空间大小约束(\mathcal{L})(我们将这些称为输入列表)。
现在,假设提议者是被动的(即理性的,但不接受贿赂)。由于每个输入的大小都可以是 \mathcal{L},因此列表的最终并集的大小可以 \geq \mathcal{L}。现在,构建者(或没有 PBS 的提议者)被限制从包含列表中选择交易; 它将选择支付最高的 \mathcal{L} 个交易,其余的将不会执行。因此,包含列表提议者只会想要包含最高的 \mathcal{L} 个交易。因此,之前对包含列表所做的所有分析都适用于包含列表提议者数量的比例因子(Fox et al.,FOCIL,COMIS)。
但是,在存在贿赂对手的情况下,情况看起来会非常不同。假设一方被贿赂足够(我们将在段落末尾量化这一点)以排除一个支付最高的 \mathcal{L} 个交易,并将其替换为第 (\mathcal{L}+1)^{th} 个交易。构建者现在收到一个包含 \mathcal{L}+1 个交易的包含列表,并且可以选择排除任何交易。对手可以进一步贿赂构建者以排除目标交易。由于列表中有一笔额外的交易,因此可以在不违反包含列表属性的情况下形成区块(所有交易都已执行,或者区块空间已满)。回到该方的激励,如果它是唯一偏离选择最高的 \mathcal{L} 个交易的方,那么它将是来自第 (\mathcal{L}+1)^{th} 个交易的费用的唯一接收者。这可能大于收到的效用(如果目标交易的 f_t 不是插入交易的 f_{\mathcal{L}+1} 的 n 倍大)。即使在最坏的情况下,所需的贿赂也只会略大于 f_t/n。
总而言之,如果区块已满,则允许排除交易的包含列表属性是本文中希望避免的设计属性。因此,我们将输入列表的大小限制为小于 \mathcal{L}/n,这样即使所有方都提议唯一的交易,包含列表的大小也小于可用的区块大小。[1]
可能存在其他解决此问题的方法,例如累积的非过期包含列表和无条件包含列表,但是,这些都需要额外的状态支持,各方必须跟踪以前的包含列表。[2]
至于在使用多提议者设计时存在多少个故障点的另一个问题,来自所有方的列表聚合是最关键的故障点,但尚未得到充分研究。Fox et al. 通过从未真正聚合并且假设提议者的输入将被包含,而没有真正分析问题来回避此问题。在 COMIS 中,聚合器角色被正式化,并且他们假设此角色在他们的分析中是可信的。FOCIL 通过使用下一个区块的提议者来消除此假设,并保持与证明者委员会的检查中的故障点。但是,依赖证明者会带来很多问题。证明者没有动力进行验证; 只要他们与其他证明者一起投票,他们就可以获得奖励而没有受到惩罚的风险。因此,使用证明者进行计算比依赖证明者来确认区块的存在或验证本文中使用的证明更不可靠。
模型
在本文中,我们将参与共识的所有方都视为理性的,即试图通过交易费用、共识或贿赂来最大化他们收到的价值。我们将统一提议包含列表的每一方称为 IL 提议者,并将其输入称为输入列表。我们将聚合器称为计算这些输入列表的并集以创建包含列表的方。与之前的提案不同,我们假设每一方的输入列表大小都受到限制。如上一节所述,输入列表的大小最多可以是 k \leq \mathcal{L}/n。IL 提议者的总数被认为是 n。每笔交易 tx_i 支付 f_i 的费用以包含在包含列表中,该费用支付给包含它的 IL 提议者(由用户独立于基本费用和以太坊交易费用选择)。如果交易在多个输入列表中重复出现,则费用在所有在链上可追溯地包含它的 IL 提议者之间平均分配。
我们假设有一个外部对手,其预算足以贿赂各方采取对抗性行动。
问题陈述
问题设置包括 n 个理性方,他们在本地有权访问一组不断更新的被审查交易 (M_i)(他们的交易池)。设 M = \cap_i M_i。问题是创建一个有效交易列表,每方贡献其观察到的交易份额。
对抗模型。 我们假设 n 个参与者中的每一个都是理性的,即他们最大化自己的效用。我们假设一个贿赂对手会贿赂这些参与者以审查一个或多个交易。
定义((b,p,T)-审查抵抗)。 如果给定一个预算 b 给一个外部对手用于贿赂参与者,对于所有 t \in T(M) 的交易,至少有 p 个参与者输出一个包含 T(M) 中所有交易的列表,我们说一个协议是 (b,p,T)-审查抵抗。
协议设计旨在最大化固定 p 和 |T(M)| 的 b。更具体地说,在非多提议者包含列表设计方案中,b 通常为 O(f),但我们的协议旨在获得 b = O(n\cdot f)。
为了便于理解目标,T(M) 可以被认为是 M 中的“可行”交易子集,例如,那些支付足够高费用的交易,受空间限制的约束。T 的定义取决于我们实施的协议,并且有理由说明为什么使用这样的 T。
在我们的协议中,我们假设 M_i = M。当 M_i \neq M 时,我们的协议不满足定义,因为它可能会输出在某些 M_i 中出现的更高支付交易,而牺牲交集中的一些较低支付交易。
输入列表创建机制
我们解决的第一个问题是 IL 提议者如何为其输入列表选择交易。一种简单的方法是 IL 提议者天真地选择支付最高费用的交易,而不管其他人的行为如何。但是,这种贪婪的方法不是纳什均衡。如果所有其他 IL 提议者都在贪婪地选择交易,那么对于任何 IL 提议者来说,理性的选择可能不是这样做。表 1 说明了这一点。
| 策略 | 选择的对象 | 效用 |
|---|---|---|
| 选择支付最高的 | (o_1,o_2) | 7 |
| 交替选择 | (o_3,o_4) | 15 |
表 1:选择支付最高的对象不是纳什均衡。考虑交易 (\{o_1,o_2,o_3,o_4,o_5,o_6\}),其效用分别为 (\{11, 10, 9, 6, 4, 3\}),以及三个玩家,其最大输入列表大小为 2。假设其他玩家遵循选择支付最高的交易的策略。
更可行的方法是使用混合策略,其中各方根据预定义的概率分布选择交易。偏离此分布将导致较低的预期收入。但是,混合纳什均衡可能不足够,尤其是在玩家可以等待观察其他人行为之后再进行决定的游戏中。因此,本文探讨了相关的均衡。
相关的均衡是一种情况,其中每个玩家都被建议特定的行为,并且假设其他人遵循建议,则偏离这些建议会导致较低的效用。为了防止中心化(通过要求单个已知方发送建议),我们提出了一种众所周知的算法,每个方都可以在本地运行该算法以模拟这些建议的行为。偏离该算法将导致偏离方的效用降低。
算法 1:交易包含的贪婪算法
算法 1:交易包含的贪婪算法
输入: ( n \\geq 0 ),( m \\geq 0 ),( k \\geq 0 ) (玩家数量、交易数量、输入列表大小)
输出: 所有 ( i \\in P ) 的 ( L\_i ) 数组(每个玩家的最终包含列表)
1. P \\gets \[1,\\dots,n\]
2. U \\gets \[u\_1,\\dots, u\_m\]
3. N \\gets \[1,\\dots,1\]
4. \\forall i \\in P: L\_i \\gets \[1,\\dots,1\]
5. l \\gets 0
6. **while** l < k **do**
1. i \\gets 0
2. **while** i < n **do**
1. U\_{curr} \\gets (U \\otimes L\_i) \\oslash N
2. s \\gets argmax(U\_{curr})
3. L\_{i}\[s\] \\gets 0
4. N\[s\] \\gets N\[s\] + 1
5. i \\gets i + 1
3. **end while**
4. l \\gets l + 1
7. **end while**
8. **return**\\forall i \\in P: L\_i该算法迭代地更新每个玩家的交易包含状态。每个玩家的输入列表 (L_i) 指示交易是否已包含 (0) 或未包含 (1)。该算法旨在贪婪地最大化效用值,根据其当前效用和每个交易被包含的次数来包含交易。
算法描述
考虑以下模拟协议。首先随机编号所有方。由于随机性需要在所有方之间相同,因此在协议开始之前就随机种子达成一致。一次将物品贪婪地分配给所有方。每个方选择在该时刻提供最大效用的物品。为此,它计算所有尚未选择的物品的当前效用 \left((U \otimes L_i) \oslash N\right)。第一个 (U \otimes L_i) 使 i 已经选择的所有物品的效用为 0,然后 \oslash N 除以如果方 i 决定选择该物品则共享该物品的方的数量。更新该方选择的物品列表(0 表示已选择该物品),并且还更新选择该物品的方的数量。重复该过程 k 次,以便每个方选择 k 个物品。该协议实现了相关的均衡。请注意,虽然该协议一次将对象分配给各方,但实际上,该输出一次向各方推荐所有交易。
该协议可证明地实现了相关的均衡,同时也实现了博弈论公平性属性(几乎相等的费用分配)(即将发布的论文)。由输入列表创建算法选择的所有交易的集合是 T(M),我们通过 AUCIL 实现了 (b,p, T)-审查抵抗,如下所示。
输入列表的聚合
创建输入列表后,下一步是聚合列表以创建下一个区块的包含列表。如果交易出现在包含列表中,则该交易被限制出现在下一个区块中。由于输入列表占用的空间是固定的,因此它不会受到垃圾交易的影响,因为每笔交易都在包含它的区块之前得到确认(具有足够的基本费用)。
解决此问题的一种标准方法是给一方分配一个聚合器的角色。该聚合器会计算所有输入列表的并集,并将其添加到包含列表中。但是,此聚合器现在是一个单点故障。例如,聚合器可能没有收到来自所有 IL 提议者的输入列表,因此不能期望它添加所有输入列表。但是,如果我们考虑这种情况,而仅要求它包含某个阈值数量的输入列表,那么聚合器可以策略性地省略特定的输入列表,并显着降低审查交易所需的预算。
那么,在这种情况下该怎么做呢?FOCIL 要求下一个区块的提议者包含一个包含列表,该列表是本地输入列表的超集。但是,它仍然允许某些交易不在包含列表中(由于阈值)。相反,我们寻求一种不同的方法来处理这个问题。我们拍卖聚合器的角色;但是,不是支付投标来赢得聚合器的角色,而是投标是包含列表的大小。因此,如果一方 P 提出的包含列表大于所有其他方,那么 P 将获得聚合器的角色和奖励。
算法:AUCIL 概述
参与者: 所有 IL 提议者 P_1, P_2, \ldots, P_n
步骤 1:IL 提议者广播输入列表
-
对于每个提议者 P_i:
- P_i \rightarrow_B(广播给所有方):\text{inpL}_i
步骤 2:各方将输入列表聚合到包含列表中并广播它
-
对于每个方 P_j:
- \text{incL}_j = \bigcup_{i=1}^{n} \text{inpL}_i
- P_j \rightarrow_B(广播给所有方):\left(\text{incL}_j, \ell_j = \text{size}(\text{incL}_j)\right)
步骤 3:提议者选择最高的投标包含列表
- 提议者收到:\{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\}
- 提议者选择最高的投标。
虽然通过引入聚合奖励 (u_a) 使步骤 2 具有清晰的激励,但步骤 1 和 步骤 3 不具有激励兼容性。如果所有其他方都广播其输入列表,则对于一方来说,不广播其输入列表将占主导地位。这样,它可以创建最大的包含列表,从而赢得拍卖。因此,步骤 1 不具有激励兼容性。同样,提议者没有动力选择最高的投标。拍卖中的审查制度 得到了研究并且很容易在此处应用。因此,步骤 3 也不具有激励兼容性。
回想一下审查抵抗的定义。如果某些协议满足 (b,p, T)-审查抵抗的定义,那么至少 p 个方输出一个非审查的包含列表。因此,我们要求提议者包括证明包含的投标大于 n-p 个其他投标(例如,包括 n-p 个投标)。如果提议者未能添加此类证明,则该区块将被视为无效,从而使 步骤 3 具有激励兼容性。
我们使拍卖有偏见以解决不广播的问题。首先,观察到如果没有一方广播其输入列表,那么任何一方赢得拍卖的概率都非常低;因此,广播其输入列表至少会产生将输入列表包含在包含列表中所获得的奖励。因此,如果更多的人认为保持其输入列表私密不会导致赢得概率显着增加,那么各方将有动力广播其输入列表。
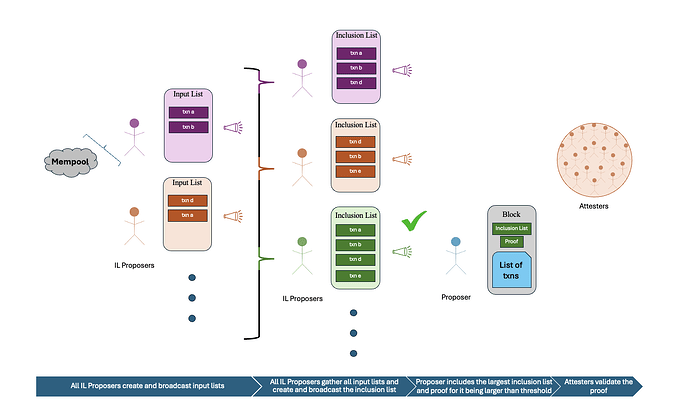 \
AUCIL-Outline1410×860 71.7 KB
\
AUCIL-Outline1410×860 71.7 KB
算法:AUCIL
参与者: 所有 IL 提议者 P_1, P_2, \ldots, P_n
步骤 0:IL 提议者生成他们的拍卖偏差
-
对于每个提议者 P_i:
- P_i 生成一个随机偏差:\text{bias} \gets \text{VRF}(P_i, \text{biasmax})
- (偏差在 0 和 \text{biasmax} 之间均匀分布,并添加到投标中。)
步骤 1:IL 提议者广播输入列表
-
对于每个提议者 P_i:
- P_i \rightarrow_B(广播给所有方):\text{inpL}_i
- (提议者将其输入列表广播给所有各方。)
步骤 2:各方将输入列表聚合到包含列表中并广播它
-
对于每个方 P_j:
- \text{incL}_j = \bigcup_{i=1}^{y_j} \text{inpL}_i
- (其中 y_j 是方 P_j 收到的输入列表的数量。)
- P_j \rightarrow_B(广播给所有方):\left(\text{incL}_j, \ell_j = y_j + \text{bias}\right)
- (各方声明他们的投标并添加偏差。)
步骤 3:提议者选择最高的投标包含列表
- 提议者收到:\{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\}
- 提议者选择最高的投标并将其添加到区块 (\text{incL},\ell)。
- 提议者添加证明,证明最高的投标大于 n-p 个其他投标。
步骤 4:证明者对区块的有效性进行投票
- 对于每个证明者:
- 证明者收到:\{(\text{incL}_1, \ell_1), (\text{incL}_2,\ell_2), \ldots, (\text{incL}_n,\ell_n)\} 和 (\text{incL},\ell)
- 证明者验证附加的证明,并且仅当证明正确时才进行投票。
- 如果区块收到的投票超过阈值,则该区块被认为是有效的。
通过上述算法,我们声明除非绘制的偏差大于 \text{biasmax}-1,否则该方有动力广播输入列表。即使偏差大于 \text{biasmax} -1,仍然存在混合纳什均衡,各方仍然可以选择广播。
审查抵抗
通过贿赂 IL 提议者进行审查
对手可以采取的第一个攻击步骤是从输入列表中删除交易。为此,假设向那些被分配包含目标交易的 IL 提议者提供贿赂。该贿赂应足以确保以概率 1 将目标交易从每个输入列表中排除。假定(目前)这些 IL 提议者中的每一个都会计算步骤 3 中所有观察到的输入列表的并集。
Fox et al. 分析了多提议者场景所需的贿赂。在他们的情况下,假设交易在所有提议者中重复出现。如果交易支付 f_i 的费用(对他们来说,费用较高),那么对手将不得不支付 n 倍的费用才能审查该交易。
在我们的例子中,分析是相似的。如果交易在 \kappa_i 个输入列表中重复出现,那么预期的所需贿赂是 \kappa_i f_i。参数 \kappa_i 与 \frac{n\cdot f_i\cdot k}{\sum f_i} 成正比,其中 \sum f_i 是协议选择的所有交易支付的费用之和。作为对此数字的直观理解,我们的结果之一确保了每笔交易的收入分配是公平的,因此,假设每笔交易都给出相同的效用。(假设存在两笔交易,分别支付 15 和 5 的费用,那么前一笔交易将包含在后一笔交易的三倍多的输入列表中。因此,收入是相同的)。n\cdot k 表示可用的总插槽,其中具有费用 f_i 的交易将占用 \frac{f_i}{\sum f_i} 的总空间,以维持相同的收入假设。因此,如果贿赂 IL 提议者以将交易从输入列表中排除是主要行动(与我们将要提到的聚合器的贿赂相比),那么该协议将具有 (b=O(\frac{nkf_i^2}{\sum f_i}),n, T)-审查抵抗性。
通过贿赂聚合器进行审查
在另一种贿赂攻击中,对手可以贿赂一方以通过排除包含目标交易的所有输入列表来减少其投标。因此,每一方的投标都会减少 \kappa_i。这与绘制的偏差小于绘制的偏差 \kappa_i 相同。\text{biasmax}-1 的偏差应该具有几乎 0 的获胜概率,因此,将一方偏差减少到 \text{biasmax}-\kappa_i 实际上意味着对手正在贿赂该方不参与拍卖。从我们的分析来看,对手必须预期支付 \frac{\kappa_i n}{biasmax} 个各方(每个各方的偏见都大于 n-\kappa_i)u_a 的贿赂,才能使其不包括包含目标交易的输入列表。将 \text{biasmax} 和 u_a 设置为 \sqrt n 和 \sqrt n \cdot u_{il} \geq \sqrt n \cdot f_i,我们实现了 (b = O(\frac{n^2kf_i^2}{\sum f_i}),n-\kappa_i\sqrt n+1,T)-审查抵抗。
结论
我们概述了一种所有方都有动力遵循的输入列表构建方案。在有限大小的包含列表的范围内,我们实现了显着的审查抵抗保证(与包括交易的各方数量成正比)。然后,我们研究了一种聚合方案 AUCIL,该方案利用拍卖来激励各方包含最大的包含列表。AUCIL 确保聚合器有动力将所有输入列表添加到交易中。我们还在分析联盟如何影响审查抵抗保证,并将很快发布结果。同时,很高兴听到对 AUCIL 和包含列表构建机制的想法。
-
请注意,使用 EIP-1559,当区块空间已满时,填充区块的成本会扩大。因此,如果网络没有拥塞,并且对手正在插入人工交易以提高拥塞,那么跨多个区块的贿赂成本将会很高。↩︎
-
我们实现了与无条件 IL 相同的“无条件”属性,而无需分配独占的包含列表空间。↩︎
- 原文链接: ethresear.ch/t/aucil-an-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊 2026年协议级更新确定 3 大方向 134 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 98 浏览
- 网络匿名化内存池 75 浏览
- 如何去中心化构建区块? 272 浏览
- 一切皆市场 283 浏览
- Builder Codes & ERC-8021:修复链上归属问题 303 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 340 浏览
- “夺旗”竞赛继续! 291 浏览
- EVM Gas 分析:新的执行跟踪数据 300 浏览
- 质押和链上信贷市场之间的微妙张力 400 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 346 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 296 浏览

