RISC0 算法分析，分段证明 — 第一部分

RISC0 算法分析，分段证明 — Part1

简述

RISC0 是一个基于 RISCV 指令集和 STARK（可扩展的知识透明论证）的 zkVM (零知识虚拟机)。RISC0 证明系统由分段证明、递归和 STARK 到 SNARK 证明组成。由于分段证明占据了最多的内存和计算量，我们专注于分析分段证明过程，包括 RAP、DEEP-ALI 和 FRI。

1. 目的

RISC0 是一个基于 RISCV 指令集和 STARK（可扩展的知识透明论证）的 zkVM (零知识虚拟机)。我们将介绍 RISC0 中的整体证明过程，并重点分析分段证明，包括其原理和分段的详细证明过程。最后，我们将比较 RISC0 和其他 zkVM 的相似之处、不同之处和优势。

2. RISC0 证明过程

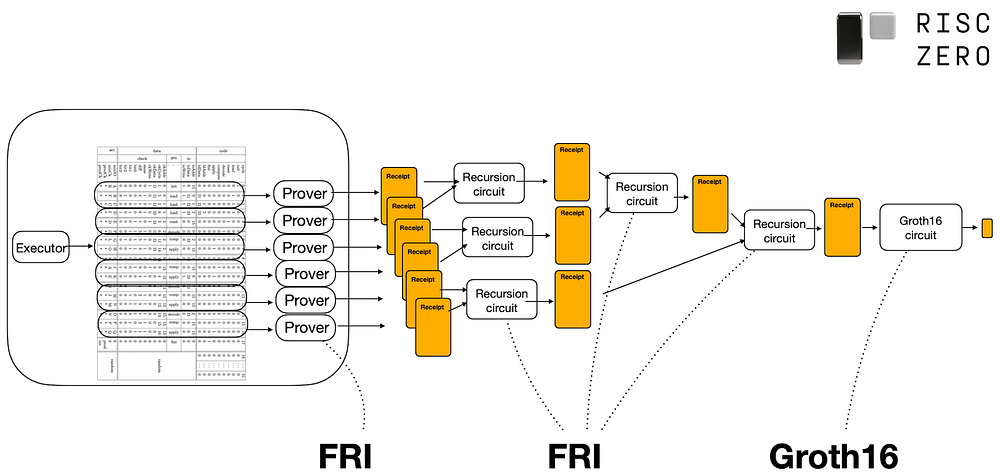
图 1 RISC0 证明过程，来自 https://dev.risczero.com/proof-system/

如上图所示，对于一个要证明的程序（由无数个 RISCV 指令组成，由 rust 等高级语言编译）及其给定的输入，RISC0 zkVM 将执行该程序并生成一个证明文件，以证明该程序已正确执行。同时，证明文件不能包含任何敏感信息，例如执行过程中生成的数据和私有输入。为此，RISC0 zkVM 将：

A. 执行程序，将程序分成多个段，并记录每个段的输入和输出；

B. 证明每个段并获得每个段的 Receipt。此步骤通过 STARK/FRI 协议证明；

C. 使用递归证明将上述步骤中获得的 Receipts 合并为一个 Receipt，以便在证明不同大小的程序时可以生成相同长度的证明文件；

D. 通过 Groth16 将递归证明获得的 Receipt 转换为 snark 证明，以进一步减小证明大小。

分段证明占据了最多的内存和计算量。下面将详细分析分段的详细证明过程。

3. 代数结构

分段证明是基于 STARK 协议的证明系统。为了方便描述和理解分段证明，我们需要介绍证明过程所需的代数结构，如下图所示。

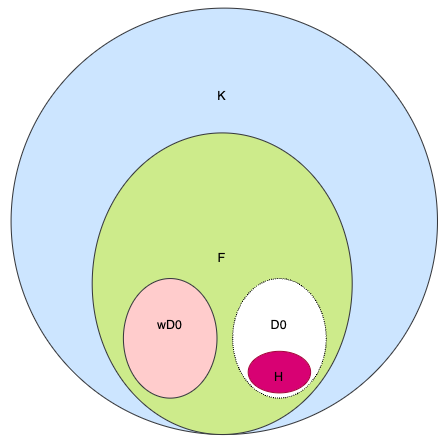
图 2 分段证明中的代数结构

其中，

F, 是有限素域 Fp，即 F = Fp，p = 2³¹ — 2¹⁷ + 1，Fp 是 Baby Bear 素域；

K, 是 F 的有限扩张域，K = F[X]/(X⁴ + 11)，即多项式环 F[X] 关于理想 (X⁴+11) 的商环。很容易知道 X⁴+11 是 F 上的不可约多项式，那么 K 相对于 F 的扩张数为 4，K 中的 1 个元素通常需要 F 中的 4 个元素来表示；

为什么我们需要扩张域 K？ 为了保证安全性，挑战值所在的样本空间必须足够大。F 中的元素数量只有大约 2³¹，而 K 中的元素数量大约为 2¹²⁴。

D0, 乘法群 F/{0} 的循环子群，其元素数量 |D0|，例如 2²⁰；

H, D0 的子群，其元素数量 |H|，例如 2¹⁸，跟踪域；为什么我们需要循环子群 H？因为在插值和计算单变量高阶多项式 f(x) 时，使用 NTT/iNTT 进行高效计算，而 NTT/iNTT 的前提是 x 必须是循环子群中的元素。

H 称为跟踪域，这在 STARK 中很重要，因为所有多项式的大部分计算和表示都在 H 上执行。

wD0, D0 的左陪集，w 是 F 中不属于 D0 的元素，例如 wD0 = {3*d | d∈D0}，称为承诺域或评估域。为什么需要左陪集 wD0？引入 w 是为了实现零知识。同时，在循环群的陪集上进行多项式计算只需要简单地变换多项式系数，也可以使用 NTT/iNTT；

在执行段证明时，通常需要在跟踪域 H 上计算或表示多项式，并在承诺域 wD0 上进行多项式承诺。

4 分段证明

分段证明的目的是证明顺序指令流的执行过程是正确的。这个问题被转换为证明执行的中间过程（trace）满足多项式方程组的约束，然后转换为证明某个多项式的度数相对较低（即，低度测试问题）。最后，使用 FRI 协议来证明多项式的度数相对较低。分段证明主要由 set-up 阶段、RAP、DEEP-ALI 和 FRI 组成，如下图所示：

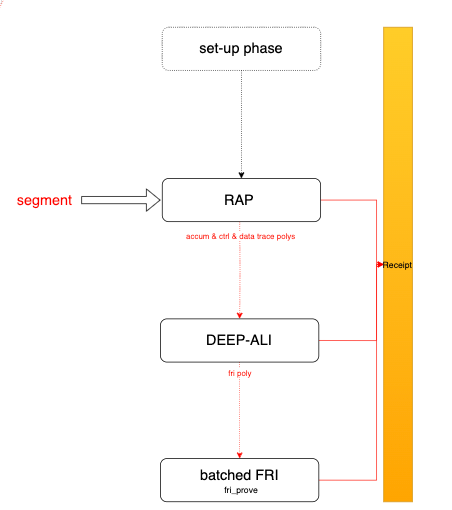
图 3 分段证明

set-up 阶段配置一些证明参数，例如 FRI (Fast Reed-Solomon Interactive oracle proof of proximity) 协议查询阶段的查询次数，trace 的最大长度等。同时，它还将生成 trace 之间的约束多项式（以源代码的形式给出，这部分源代码生成约束多项式在 trace 上的函数值）。值得注意的是，对于一个经过验证的程序，set-up 阶段只需要执行一次，稍后将不再讨论此过程。

RAP (Randomized Algebraic intermediate representation with Preprocessing) 将执行该段并记录执行过程中的中间数据（例如寄存器值、内存访问等），目的是计算 trace polys，包括 ctrl & data & accumulate polys 和 commitments，这将在后面详细描述。

DEEP-ALI (Domain Extending for Eliminating Pretenders — Algebraic Linking IOP) 将计算 check 多项式和 fri 多项式。Check 多项式是指将 trace 多项式代入相应的约束多项式并除以 vanish 多项式后得到的结果。这是 STARK 中的关键一步，因为证明程序执行过程正确等价于证明 check 多项式是一个多项式且该多项式的度数相对较低。为了确保 check poly 的计算过程正确，需要计算 deep 多项式，最后将所有 deep 多项式合并为一个 fri 多项式。

FRI (Fast Reed-Solomon Interactive oracle proof of proximity) 旨在证明 fri 多项式的度数小于或等于 trace 域大小。下面，我们将详细介绍其过程。

5 RAP

RAP 的目的是计算控制和数据多项式组，它们表示段执行过程中数据寄存器和控制寄存器的值。此外，为了证明内存访问行为的正确性和范围检查，需要生成一组新的多项式：累积多项式组，用于置换论证和查找论证。

此外，需要使用 merkle 树来分别计算控制 & 数据 & 累积多项式组的多项式承诺值。

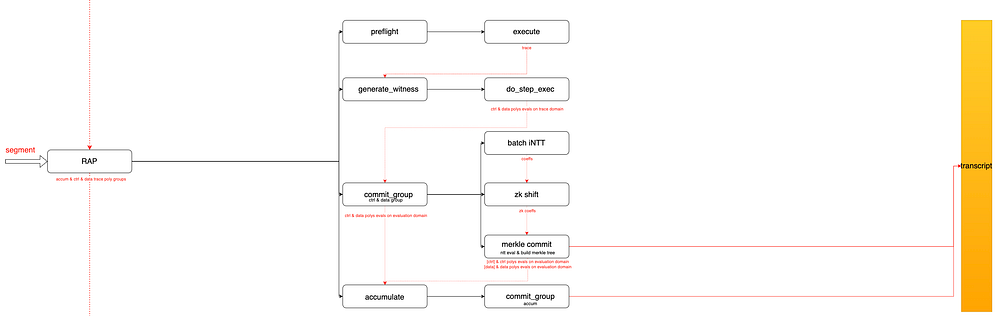
如图 4 所示，RAP 由以下步骤组成：

5.1 preflight/execute，按顺序执行段中的指令，将每条指令访问的寄存器地址和值记录为 raw_trace，并注意数据类型为 uint32；

5.2 generate_witness，将 raw_trace 中的数据转换为 F 中的元素，根据 raw_trace 计算每个周期中所有寄存器的值，从而获得一个二维矩阵。任何一行代表某个周期中的所有寄存器值，任何一列代表所有周期中某个控制或数据寄存器的值。同时，该列被视为跟踪域 H 中控制或数据多项式的函数值，因此周期数必须小于或等于 H 中元素的数量 |H|。如果周期数小于 |H|，则用 0 填充矩阵中缺少的行。

5.3 对于控制 & 数据多项式组（每个多项式由 H 上的函数值表示），计算多项式的承诺值：

5.3.1 iNNT 计算每个多项式的系数，注意每个多项式的系数长度为 |H|；

5.3.2 将每个多项式的系数乘以 3^i，例如第 n 个多项式的系数为 cn_0,​​…, cn_i, …, 则 cn_i = cn_i*3^i；

5.3.3 NTT 计算承诺域 3*D0 上每个多项式的函数值；

5.3.4 计算控制和数据多项式组在承诺域上的函数值的 merkle 树，

然后我们将得到 2 个 merkle 树，merkle 树的根节点就是承诺值。

5.4 对于控制 & 数据多项式（由 H 上的函数值表示），为了保证内存访问合法性和范围检查，需要引入置换约束和查找约束所需的多项式，即累积多项式。为此，需要：

5.4.1 基于现有控制和数据多项式组的承诺值，为每个置换约束和查找约束在扩展域 K 中生成一个随机挑战值；

5.4.2 计算与每个置换和查找约束对应的多项式（由 H 上的函数值表示），这些多项式统称为累积多项式组；

5.4.3 类似于 5.3 中的操作，对于累积多项式组，计算其承诺值。

6. DEEP-ALI

为了方便描述，我们将控制多项式组、数据多项式组和累积多项式组中的所有多项式称为 trace 多项式，将所有 trace 多项式在 trace 域 H 上的所有函数值称为 traces。

我们的目标是证明段中指令执行的正确性。这个问题被简化为 trace 中某些元素之间必须满足的一组约束（表示为一组多元多项式方程），而这个问题的成立等价于约束多项式能够整除 trace 域 H 上的 vanish 多项式。DEEP-ALI 将取约束多项式和 vanish 多项式的商以获得 check 多项式并计算其承诺值。此外，为了确保 check 多项式的计算正确，将计算 DEEP 多项式，最后将所有 DEEP 多项式组合以获得 FRI 多项式。

check 多项式的定义如下：

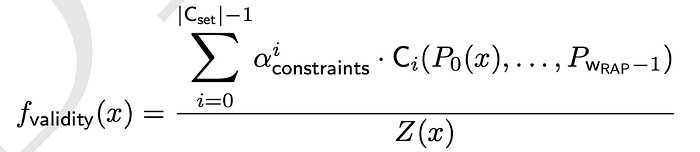
check poly/validity poly 定义

其中，

α_constriaints，是一个随机挑战值，属于扩展域 K；

Ci，是一个约束多元多项式；

P0(X), …, 是一个 trace 多项式；

Z(X)，是 trace 域上的一个 vanish 多项式，Z(X) = X^|H| — 1, |H| 是 trace 域 H 中元素的数量；

请注意，f_validity 是 RISC0 代码中的 check_poly，因此在本文中，我们将其称为 check 多项式。

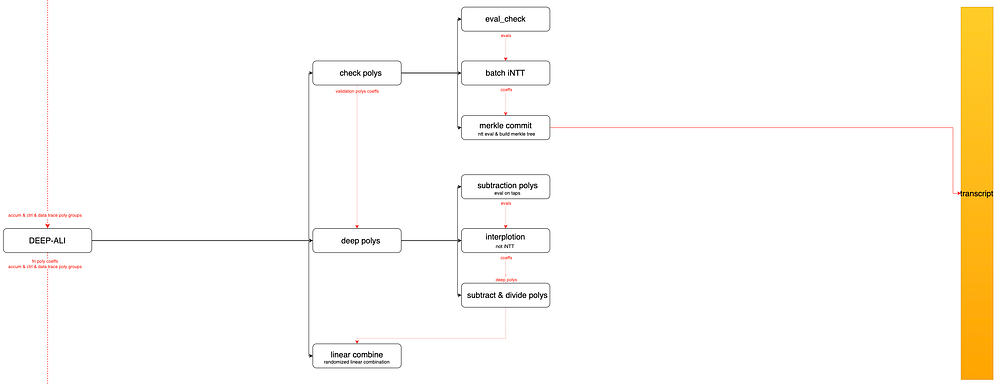
如图 5 所示，DEEP-ALI 由以下步骤组成：

6.1 eval_check，即在评估域 wD0 上计算 check 多项式的函数值。由于 check 多项式的最高次数为 4*|H|，因此需要在评估域 wD0 而不是 trace 域 H 上计算函数值；

6.2 batch iNTT 获得 check 多项式的系数，因为 check 多项式被认为是 K 上的一个度数为 4*|H| 的多项式，它可以被认为是 F 上的 16 个度数为 |H| 的多项式，从而获得一个由 16 个多项式组成的 check 多项式组；

6.3 计算 check 多项式组中每个多项式在承诺域上的函数值，并使用这些函数值构造 merkle 树以获得多项式组的承诺值；

6.4 计算 deep 多项式，其定义为：

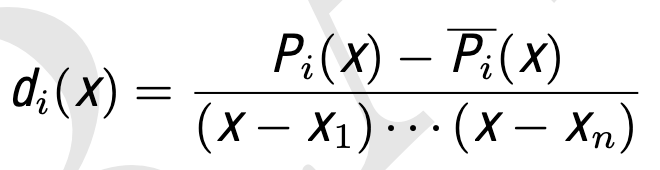
deep poly 定义

deep polys 的目的是确保上述 check polys 是诚实计算的。

我们认为，如果在扩展域 K 中取一个随机值 z，并且 eval_check 中等式的两边相等，则 check polys 是诚实计算的（存在soundness 错误）；

当且仅当有理函数是多项式函数时，check polys 才是诚实计算的。

其中 Pi 是 trace poly 或 check poly；

__Pi 是通过插值计算“约束多元多项式函数值”所需的不同点的 Pi 函数值而获得的多项式，例如 xi = ωz，ω 是 trace 域 H 的生成器。

6.5 组合所有 deep 多项式以获得 fri 多项式。

7. FRI

FRI 的目的是证明 fri 多项式的度数小于或等于 trace 域 H 的大小。如果 deg(fri(X)) ≤ |H|，则 check 多项式是度数 ≤ 4*|H| 的多项式，并且 check 多项式是诚实计算的。然后 trace 中的元素满足约束多元多项式方程组，并且段中的指令被诚实地执行。

FRI 包括 commit 阶段和 query 阶段，如图 6 所示，它由以下步骤组成：

7.1 commit 阶段，fri poly 的度数以 16 的倍数减少到 256，然后有 log(16, deg(fri)) 轮，并且每一轮生成的多项式都会被承诺。对每一轮执行以下计算：

7.1.1 fri poly 是扩展域 K 上的一个 |H| 次多项式，可以被认为是四个域 F 上的一个 |H| 次元素。通过 batched NTT 计算四个多项式在承诺域上的函数值；

7.1.2 使用 fri 多项式在承诺域上的函数值，构建一个 merkle 树以获得承诺值；

7.1.3 将 fri 多项式分成 16 个部分以获得 16 个子多项式，然后使用随机线性组合来获得下一轮的 fri 多项式。

7.2 Query 阶段，对于所有承诺的多项式，包括控制多项式、数据多项式、累积多项式、check 多项式、log(16, deg(fri)) 轮 fri 多项式，打开这些多项式的证明。

7.2.1 在承诺域中选择一个随机挑战值 g0；

7. 2. 2 构建评估集中的元素，即 g0, g0*16, …, g0^(16*round_n);

7.2.3 打开 g0 处的控制多项式、数据多项式、check 多项式的证明，并打开 g0^(16*round_i) 处第 i 轮 fri 多项式的证明。

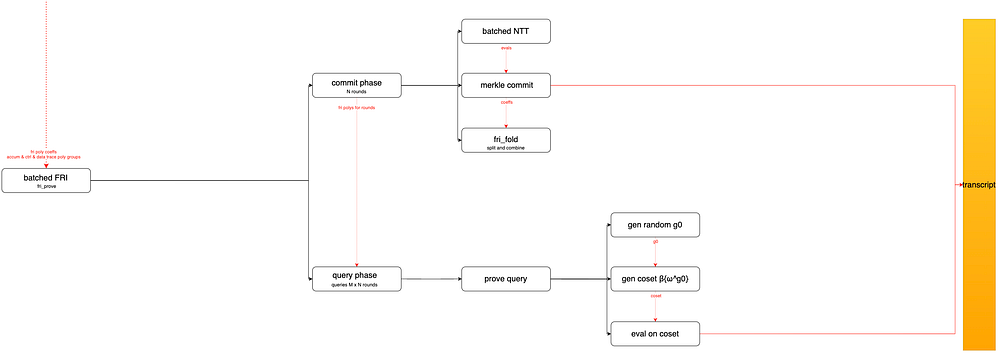
图 6 FRI

8. 与其他 zkVM 的比较

• 原文链接： medium.com/@CFrontier_La...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～