ZK纪事：电路（第一部分）

为了获得更具互动性的体验，请在我的个人博客 Arkana 上阅读本文。

在学习了上一篇文章之后，我们已经了解了第一个证明系统，即 sum-check 协议。

Sum-check 不错，但说实话：对布尔超立方体的求和并没有特别的吸引力。我们需要一个更通用的框架来表示任意计算，从而允许我们证明更广泛的事情。

为此，我们首先需要弄清楚可验证计算的核心问题：如何表示计算本身。

有很多方法可以对计算进行建模，所以今天，我们将只关注一个用于实现此目的的构造：电路。

太棒了！明确了目标，让我们开始吧！

电路 101

电路是计算的一种非常通用的模型，这已经不是什么秘密了。

你电脑的 CPU 由数千万个微小的晶体管构建而成，这些晶体管构成逻辑电路，使你的电脑能够执行极其广泛的操作——从在你的计算器应用程序中执行简单的乘法，到控制你正在阅读的屏幕的像素等复杂任务。

除非这段文字最终出现在纸质版本上，那样你就不会看像素了……但你明白我的意思。

太棒了！但我们这里讨论的是数学，而不是从晶体管和物理电路的角度来考虑。我们需要对电路进行严格的定义——一个我们可以用多项式和协议来处理的定义。

所以，这就是我们定义它们的方式：一个布尔电路是一个 有向无环图 (DAG)，其中：

• 内部节点（称为门）表示运算（AND、OR、NOT 等）
• 边（或线）在门之间携带布尔值（0 或 1）
• 输入节点没有传入的线——它们是我们输入数据的地方
• 输出节点没有传出的线——它们产生最终结果

要求电路是 DAG 非常重要：它建立了从输入到输出的流程，简洁地表示了一个计算。

这是一个例子：

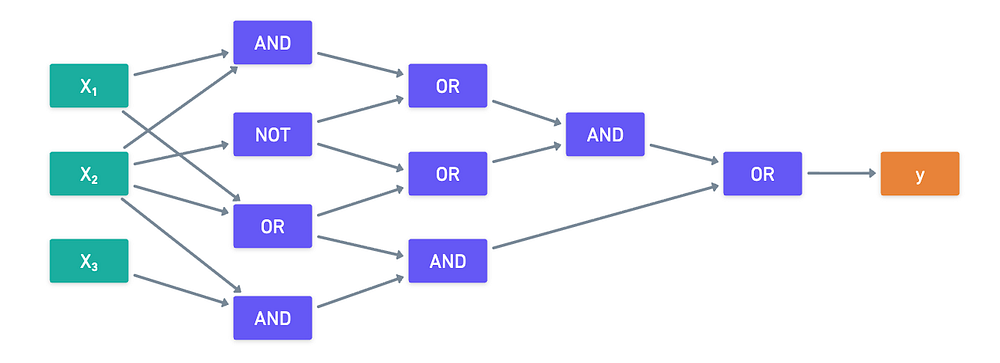
有些公式将否定作为输入，从而使输入的数量成为原始 n 输入的函数。这只会影响成本分析，但公式是完全等效的！

电路可以表示很多东西。在这种布尔形式中，它们表达了我们想要在一系列输入上评估的逻辑条件。例如：我是否超过 30 岁，并且我是男性，并且我有一份工作或者其他某种形式的收入来源？我们可以将这个语句表达为一个简单的布尔电路！

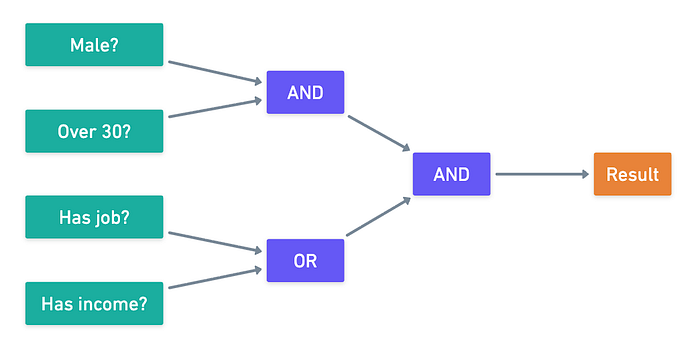
总而言之，电路只是一个具有一些良好属性的计算的静态配方，例如确定性（相同的输入总是返回相同的值）和可组合性（电路可以链接在一起，就像在计算机中一样）。

最后，我们用门的数量来衡量电路的大小 ($S$)，而深度 ($D$) 是从任何输入到任何输出的最长路径。

有了这些，我们就有了第一种描述计算的方法。当然：我们只允许布尔变量——但这似乎并没有阻止计算机被用于几乎任何任务。

但是，我必须提醒你：本系列的目标是证明关于计算的语句。因此，现在我们的重点应该转移到尝试证明关于这些电路的一些事情。

这就引出了我们的下一个问题。

电路可满足性

虽然我们可以尝试证明给定一组输入，布尔电路的输出是否正确，但这可能不会是一个太有趣的问题（至少目前是这样）。毕竟，输出也是一个布尔值，这意味着我们只有两种可能的输出。

如果我们可以有多个可能的输出，那将是另一回事。我们将在稍后探讨这个想法！

或许我们可以考虑更有趣的事情。

那么这样如何：给定一个电路，如果我们问自己是否有任何输入使输出为 1 呢？

当这种情况发生时，我们说输入满足电路。确定一个电路是否具有任何满足条件的输入被称为电路可满足性问题，或简称为 CSAT。

这实际上是一个非常重要的问题，我们很快就会知道。许多其他问题，如因子分解或图着色，都可以简化为电路。不过，我们今天不会深入研究这些转换——但这绝对是可能的。

我们将在几篇文章中继续讨论这个问题！

CSAT 本身就是一个具有挑战性的问题，但今天，我希望我们更进一步。我们不仅要问是否存在解决方案：我们今天的目标是证明我们确切地知道存在多少个解决方案。换句话说，我们想计算所有可能的输入组合，这些组合对电路的输出为 1。

这就是我们所说的电路可满足性的计数版本，写为 #SAT（# 符号表示计数）。

再一次，我敢打赌你想知道我们为什么要关心这个问题。公平地说，这是对今天的努力的一个合理问题。找到一个问题的解决方案比枚举所有可能的解决方案感觉更自然。虽然在某些情况下这可能是可取的，但我希望给你两个不同的理由来关注 #SAT：

• 首先，这是一个比 CSAT 严格更难的问题。因此，如果我们能够有效地处理 #SAT，我们几乎可以保证也能够有效地处理 CSAT——我们只需要证明满足条件的输入的数量大于零！
• 其次，我们选择这个问题是因为它的数学表示，考虑到我们目前的知识，这恰好是非常方便的。有一种非常简洁明了的方法来表示这个 #SAT 问题：如果我们将电路解释为一个具有 n 个布尔输入的函数 ϕ(X)，那么我们可以将满足条件的组合的数量表示为：

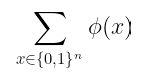
可以对所有可能的组合求和，因为不满足条件的组合会导致 ϕ(x) = 0。

你可以想象，找到这个量（满足条件的组合的数量）是一个非常难的问题。已知最快的算法的性能类似于简单的蛮力方法，即遍历所有可能的组合。

至于我之前谈到的便利性，你是否注意到 #SAT 表达式看起来与 sum-check 表达式惊人地相似？我们只是在布尔超立方体中计算函数在输入集合上的和。这是一个明确的提示——我们只需要弄清楚如何将 sum-check 应用于我们的新问题，我们就会免费获得一个验证算法！

转换电路

太棒了！那么，假设我们有一些二进制电路 ϕ(X)。

不幸的是，电路的布尔性质成为一种限制。要应用 sum-check 协议，我们需要在0 或 1 以外的点上评估 ϕ(X)，但是我们的电路无法处理……

目前是这样！

我们需要以某种方式扩展这个函数来处理其他输入值。由于我们的电路是由门组成的，所以我们只需要找到一种方法来扩展这些门，以便它们在输入为二进制时表现如你所期望的那样，但仍然能够处理其他值作为输入。

那么，我们该怎么做呢？

嗯，我们目前还没有太多数学工具可供使用——事实上，我们学到的唯一有用的构造是多项式。但这已经足够了：我们尝试将门表示为多项式怎么样？

作为一个小练习，你可以尝试自己想出一些表达式。这里，我将添加一个小剧透模块，以防你想尝试一下！

剧透模块

这是 AND 门的 polynomial 表示：

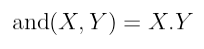
这将是 OR 门：

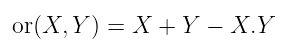
否定将是：

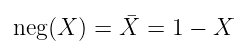
当然，其他逻辑门也有它们各自的多项式表示。例如，XOR 门可以通过 AND、OR 和 negation 门的组合来构造，这将导致一个多项式，该多项式将是此处涉及的各个多项式的组合。

结果表达式将是 XOR(X,Y) = X(1 - Y) + (1 - X)Y。如果你感到有点不安，请自己尝试一下！

太棒了！通过用这些多项式替换每个门，我们实际上是在直接扩展它们：这些门在布尔输入时的工作方式与你期望的一样，但在某些有限域中输入其他值时会做其他事情。

还记得我说拥有多个可能的输出会很有趣吗？好了，你现在看到了！

实际上，我们已经将初始布尔电路 ϕ(X) 转换为一种新型的构造，称为算术电路，我们将其表示为 φ(X)。

算术化

现在，我希望我们停在一个小细节上。看看 AND 门：

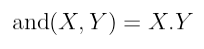
现在我们已将其扩展到有​​限域中的输入，可以直接将其称为乘法门。毕竟，乘法是我们域中的一种原始运算。

相反，OR 门看起来不那么原始。人们可能想知道我们是否需要保持这些门原样，或者是否可以将它们解包为更简单的操作。

好吧，我们在有限域中拥有的另一个原始运算是加法。那么，我们只使用加法和乘法门怎么样？这可能吗？

当然，这样做完全有可能！

在你问之前：一些数字 b 的减法是通过将其乘以 1 的加法逆元来实现的，即域 𝔽ₚ 中的 p - 1(。也就是说，要得到 a - b，我们计算 a + (-b)，其中 -b = (p-1)·b。

这就像乘以 -1！

这个过程非常重要，它甚至有自己的名字：算术化。

太棒了！我们现在有一种将布尔电路扩展为算术电路的方法，这样它们就可以处理给定域 𝔽 上的任何输入。

请注意，我们的算术电路 φ(X) 基本上等效于多项式 g(X)，它是通过门函数的组合获得的。

通常，它是一个非线性多项式。

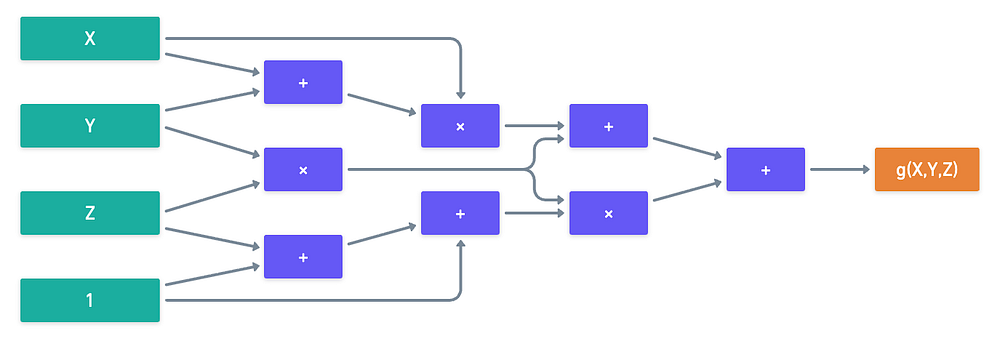
这将导致 g(X,Y,Z) = YZ² + X² + YX + 3YZ

由于 φ(X) 是某个域 𝔽 上的多项式，我们可以直接应用我们值得信赖的 sum-check 协议来评估可满足性！

所以你看——我们现在已经看到一个可以转换为 sum-check 协议实例的问题 (#SAT)。

我们需要解决一些其他的细微之处，比如弄清楚 𝔽 需要多大才能使可靠性误差变小——但我们现在不需要太关心这个问题。我的目标是尝试传达核心思想，其中算术化是一个重要的思想。

计算成本

如果你来这里是为了了解核心概念，我认为可以跳过这部分。如果是这种情况，请跳到下一节！

虽然没有必要深入研究完整性和可靠性分析（因为它与我们已经为 sum-check 所做的分析非常相似！），但讨论一下计算成本是有意义的。

在这里，我们不应该将 φ(X) 视为多项式，而应将其视为计算配方。毕竟，我们没有结果多项式的系数，而是一组加法和乘法门。

我们问自己：这是否有任何实际后果？因此，我们需要关注对协议中每个参与者的执行时间的影响。

让我们从证明者开始。他们需要在 ${0,1}ⁿ$ 中的每个输入上评估电路。每次评估都需要单独评估 $S$ 个门中的每一个，因此总成本为 $O(S \cdot 2ⁿ)$。每轮中的部分和变得越来越便宜，因此总证明者时间仅为 $O(S \cdot 2ⁿ)$。

是的，它比简单的 sum-check 更昂贵。电路越大，情况就越糟。但请记住：证明者仍然拥有强大的硬件！

相反，验证者总共执行 $O(n)$ 轮 sum-check（每个变量一轮），每轮仅检查简单的多项式方程。

此外，如果我们假设 oracle 访问，则验证者成本保持在 $O(n)$。但是，在实践中，验证者可以自己运行电路（如果他们知道电路，当然），因此不必信任一些外部来源（oracle）。如果他们这样做，那么我们需要包括电路评估成本，并且验证者运行时间变为 $O(n + S)$。

最后，我们的通信成本为 $O(n)$ 个域元素，因为我们在每轮中交换固定数量的域元素。

严格来说，域元素的数量取决于证明者发送的最大的单变量多项式的大小——但我们不要太担心这个问题，并假设这些将是低阶多项式。

好的，抱歉倾倒了这么多信息！所有这些最终都是为了说明：至少 #SAT 的性能严格低于 sum-check 运行时。

混合中的新成分是电路大小，$S$。如果验证时间在电路大小上是亚线性的而不是线性的，那将非常酷，就像我们目前的情况一样。通过这种方式，我们仍然可以快速验证大型电路上的计算——但电路大小的线性时间基本上给大型电路的执行时间带来了沉重的负担。

并且一些电路（即使对于简单的事情）也可能变得非常大。因此，至少，记住这一点真的很重要。

总结

我们正在稳步前进。

今天的进展似乎并不大。毕竟，我们研究的问题感觉在其适用性方面再次受到限制。

至少，#SAT 已经引导我们完成了一些表示一般计算的技术，最终使我们获得了算术电路的超级重要概念。

正如我们已经提到的，电路可以表示很多东西。但是，通过扩展它们以允许不仅仅是布尔运算，我们在表达性方面获得了很大的收益，因为现在这些电路可以使用整数表示任何任意计算，而不仅仅是 0 和 1。

理想情况下，我们想要做的是获取一些电路，而不是担心满足电路的输入，我们希望在给定的输入上简单地对其进行评估，并且能够显示电路已被正确评估，并且效率很高。

这与 #SAT 非常不同，但与我们今天也研究过的 CSAT 问题并没有太大区别！

如果我们设法做到这一点，那么我们就找到了第一个用于证明语句的真正通用的框架。

但是要实现这一目标，我的朋友们，我们首先需要了解一种新工具。这将是我们的下一个目的地！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～