科赫尔的时间攻击：从理论到实践的旅程

1996年，Paul Kocher 发表了一篇具有开创意义的论文，证明了密码运算的执行时间可能会泄露关于密钥的信息。这并非抽象密码算法中的数学弱点，而是一种利用高效实现的侧信道攻击。这项工作开创了 side-channel cryptanalysis 的整个领域，表明物理实现会以意想不到的方式泄露信息。

本教程通过三个渐进式的实现来探索 timing attacks，每个实现都揭示了挑战的不同方面。我们首先从一个简单的指令成本模型开始，来说明攻击的核心动态。然后，我们将转向更实际的实现中的实际 timing measurements，并展示现代处理器和操作系统带来的挑战。最后，我们展示了一些工程技术，以从noisy measurements 中恢复关键信号。这种渐进过程说明了 side-channel cryptanalysis 的理论基础和实际工程挑战。

预览并下载交互式 Notebook 以跟随工作代码，或者仅阅读独立帖子。

The Vulnerable Algorithm

RSA 加密和 Diffie-Hellman 密钥交换的核心是 modular exponentiation：计算 mkmodn。将底数 k 乘以 k 次这种朴素方法对于典型的加密密钥将需要数百万次运算。相反，实现通常使用高效的 square-and-multiply 算法，将其减少到大约 log⁡k 次运算。

该算法逐位处理 exponent。对于每一位，它总是对当前底数求平方。但这里有一个关键细节：当当前位为 1 时，它会执行额外的乘法。这种条件运算会产生漏洞：

def fast_exp(base, exponent, modulus):
    result = 1
    base = base % modulus
    while exponent > 0:
        if exponent & 1:            # THE LEAK: extra work when secret bit = 1
            result = (result * base) % modulus
        base = (base * base) % modulus
        exponent >>= 1
    return result

当 secret key bit 为 1 时，算法会执行额外的乘法。当该位为 0 时，它会跳过该步骤。这会在两种情况下产生可测量的 timing 差异。Kocher 的突破在于意识到对许多此类 measurements 进行统计分析可以逐位恢复整个 secret key。

Part 1: Clean Signal, Clean Results

请注意，当计算两个数字 a⋅b 模 n 的乘法时，乘法的结果可能小于或大于 n，这反过来意味着 a⋅b 可能需要模约简，也可能不需要。这反过来意味着当计算对于同一密钥 k 的 mkmodn 时，并非所有消息 m 都将花费相同的时间。对于多个消息和固定密钥，timing 的这种可变性对于我们的开发策略至关重要。

为了说明攻击，我们没有处理noisy wall-clock measurements，而是使用了一个简单的成本模型：每个 modular multiplication 的成本是一个乘法，加上减少结果所需的“trial subtractions”的数量。这个玩具模型在没有系统干扰的情况下捕获了基本的 timing 变化。请注意，在实践中，使用了更有效的 multiplication modulo 算法，但正如我们接下来将看到的，它们也同样会引起类似分布的指令可变性。

def mul_mod_with_cost(a, b, n):
    """通过 trial subtraction 进行 realistic cost modeling 的乘法"""
    x = a * b
    k = x // n
    x = x - k * n
    return x, 1 + int(k)

def fast_exp_with_cost(base, exponent, modulus):
    """具有成本计数的 LSB-first square-and-multiply """
    result = 1
    base = base % modulus
    total_cost = 0

    while exponent > 0:
        if exponent & 1:  # vulnerable conditional
            result, mul_cost = mul_mod_with_cost(result, base, modulus)
            total_cost += mul_cost

        base, square_cost = mul_mod_with_cost(base, base, modulus)
        total_cost += square_cost

        exponent >>= 1

    return result, total_cost

正如我们所看到的，指令的数量（成本或时间）遵循正态分布，因为许多小的随机成本会累加起来。这为 Kocher 的 variance distinguisher 提供了理想的统计基础。

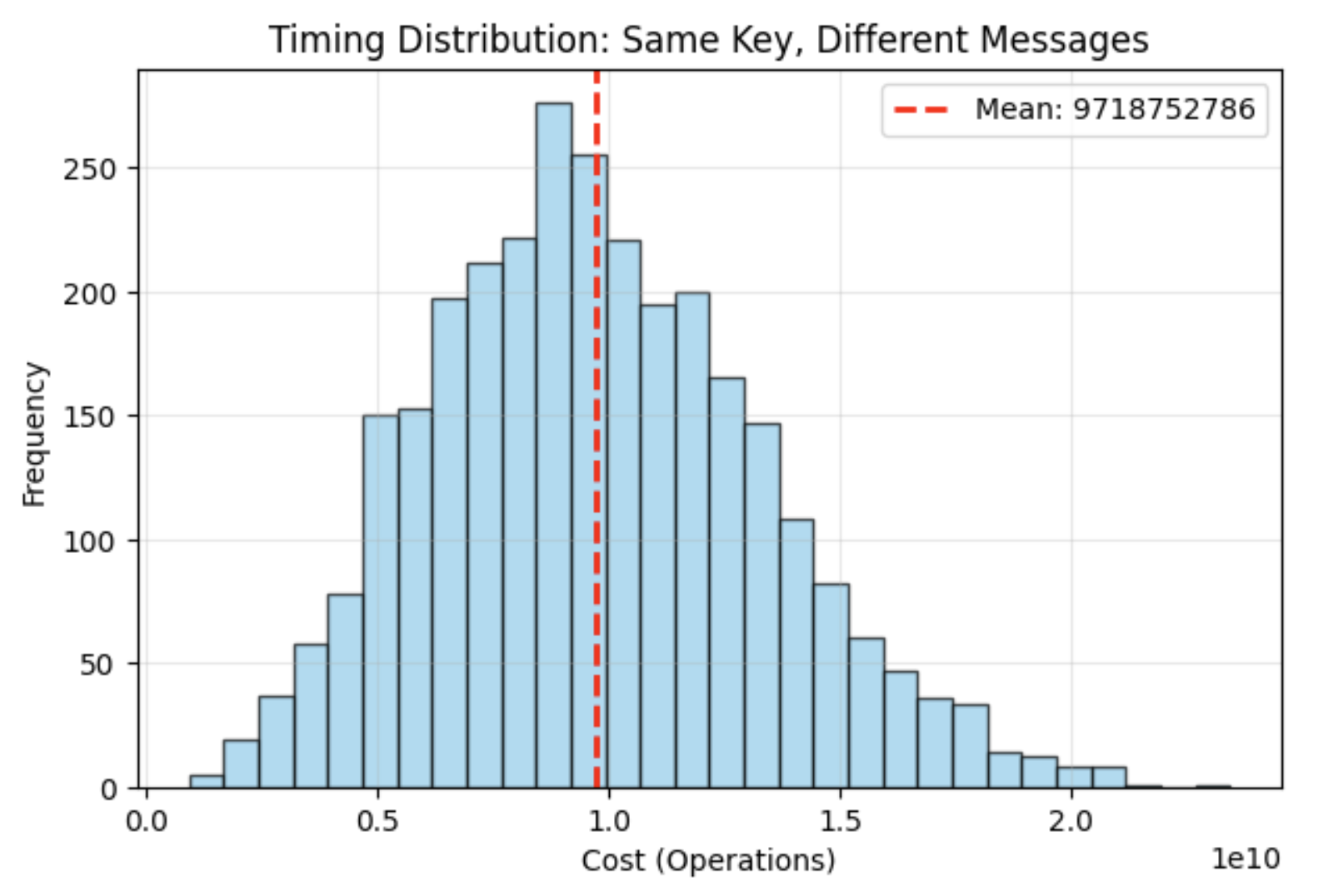图 1：Clean normal distributions 能够进行可靠的统计分析。

timing 成本的近似正态分布可以用中心极限定理来解释：modular reductions 引入了许多小的、与消息相关的variation，这些variation的行为类似于独立的噪声项。在多轮中求和，这些variation会收敛为钟形分布。这促使我们将每轮的 timing 视为近似独立，这正是 Kocher 的 variance distinguisher 依赖的假设，即将总 variance 分解为单独的贡献。

我们可以通过经验验证这种独立性假设。当我们测量早期轮次（例如，前 4 轮）和后期轮次在许多消息中的 timing 之间的相关性时，我们始终观察到低于 0.1 的系数。此类值表示非常微弱的依赖性，这支持将这些轮次视为近似独立，以用于 Kocher 的 variance 分析。

Kocher’s Variance Distinguisher Theory

关键的见解是，如果round timings 是独立的，则 variance 以加法方式分解。对于任何总成本为 Tm 的 exponentiation，我们可以写成：

Tm=prefixm(i)+suffixm(i)

其中 prefixm(i) 涵盖前 i 轮，suffixm(i) 涵盖剩余的轮次。

当我们减去前缀的正确假设时： Tm−prefixm(i,correct)=suffixm(i)⇒Var[T−prefix(i,correct)]=Var[suffix(i)]

当我们减去不正确的假设时，我们会得到一个额外的误差项： Tm−prefixm(i,wrong)=suffixm(i)±Δm(i)

由于误差 Δm(i) 在消息之间独立分布： Var[T−prefix(i,wrong)]=Var[suffix(i)]+Var[Δ(i)]

因此：Var[correct]<Var[wrong]

distinguisher 只是比较 variances：当从基线 measurements 中减去时，产生较低 variance 的假设更有可能是正确的。这种数学基础能够通过统计分析逐位 key recovery。

🔓 FULL LSB KEY RECOVERY ATTACK
==================================================
Target key: 55 = 0b110111
Assuming bit 0 (LSB) = 1 for RSA exponents
Recovering bits 1 to 5 (LSB+1 to MSB)...

Attacking bit 1 (LSB+1)
  H0 error variance: 1.10e+19
  H1 error variance: 9.70e+18
  Winner: H1
  Predicted: 1 ✅

Attacking bit 2 (LSB+2)
  H0 error variance: 7.61e+18
  H1 error variance: 7.24e+18
  Winner: H1
  Predicted: 1 ✅

Attacking bit 3 (LSB+3)
  H0 error variance: 5.96e+18
  H1 error variance: 6.14e+18
  Winner: H0
  Predicted: 0 ✅

[... continued ...]

🎯 FINAL RECOVERY ANALYSIS
Target key:     55 = 0b110111
Recovered key:  55 = 0b110111
Accuracy: 6/6 = 100.0%

对于这个简单的成本模型，我们获得了完整的 recovery，所有位都被正确识别。我们能否通过测量wall-clock time 而不是使用玩具模型来重现这些结果？

Part 2: The Challenge of Real Systems

现代计算机引入了多个timing variability来源。操作系统会中断进程以处理其他任务。CPU 根据温度和工作负载调整其时钟速度。内存缓存会产生可变的延迟。此外，Python 的垃圾回收器会引入timing spikes。这意味着在第 1 部分中可靠工作的相同 variance distinguisher 并不能保证能够有效工作。

首先，让我们看一下与第 1 部分中相同的密钥的 time measurements 的分布。我们想检查正态分布是否仍然成立，这是我们用来推断每轮时间是随机的并且与轮次无关的提示。

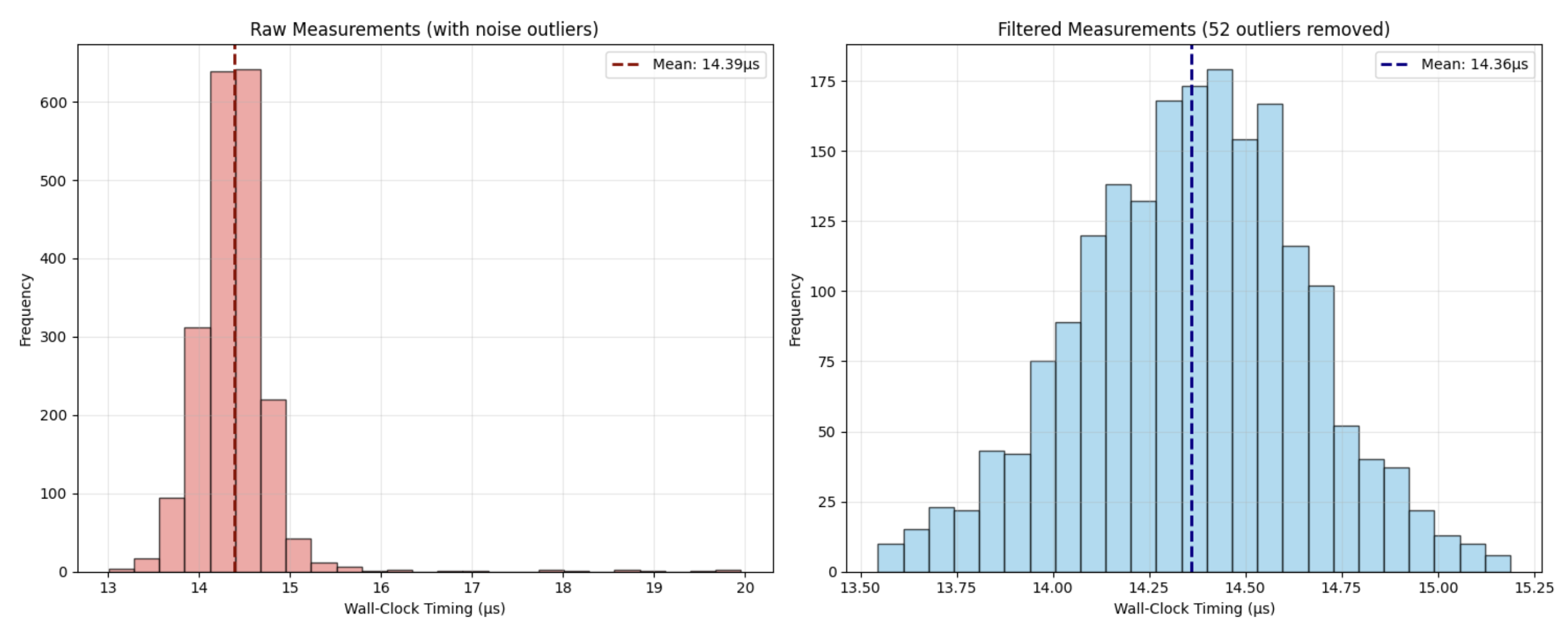图 2：删除 outliers 后，wall clock measurements 的分布也是正态的

正如我们所看到的，在删除 outliers 后，似乎存在类似的分布，这表明我们的攻击对于 timing measurements 是可行的。让我们尝试直接重现我们的攻击，使用 100 倍的 time measurement 放大倍数，以避免来自开发利用的harming 噪声。

Part 2 Demonstration
==================================================
Target key: 53 (0b110101)
Modulus: 512-bit prime
Timing source: Wall-clock (realistic noise)
Algorithm: LSB-first with assumed first bit = 1

Reality Check - Naive Wall-Clock Timing Attack
============================================================
Target key: 53 (binary: 0b110101)
Messages: 3000
Amplification: 100 iterations per measurement

Step 1: Generating random messages...
Generated 3000 random messages

Step 2: Collecting baseline measurements (full exponentiation)...
Warning: This uses wall-clock timing - expect noise!
Baseline complete. Mean: 11.491μs, Std: 0.320μs
Coefficient of variation: 2.8% (high = noisy!)

Step 3: Attempting to recover 5 bits...
Warning: With high noise, variance distinguisher becomes unreliable

🔑 Exponent Assumption:
  Bit 0 (LSB): 1 (assumed known and odd)
  Starting attack from bit 1 (second LSB)...

--- Attempting bit 1 (LSB+1) ---
Testing H0: 32769 = 0b1000000000000001 (bit 1 = 0)
Testing H1: 32771 = 0b1000000000000011 (bit 1 = 1)
Actual bit value: 0
Measuring noisy wall-clock timings...
Prediction means: H0=2.435μs, H1=3.773μs
Error variances: H0=0.11, H1=0.11
Decision: bit = 1
Result: ✗ WRONG

--- Attempting bit 2 (LSB+2) ---
Testing H0: 32771 = 0b1000000000000011 (bit 2 = 0)
Testing H1: 32775 = 0b1000000000000111 (bit 2 = 1)
Actual bit value: 1
Measuring noisy wall-clock timings...
Prediction means: H0=4.994μs, H1=6.366μs
Error variances: H0=0.10, H1=0.09
Decision: bit = 1
Result: ✓ CORRECT

--- Attempting bit 3 (LSB+3) ---
Testing H0: 32775 = 0b1000000000000111 (bit 3 = 0)
Testing H1: 32783 = 0b1000000000001111 (bit 3 = 1)
Actual bit value: 0
Measuring noisy wall-clock timings...
Prediction means: H0=7.638μs, H1=9.045μs
Error variances: H0=0.09, H1=0.10
Decision: bit = 0
Result: ✓ CORRECT

--- Attempting bit 4 (LSB+4) ---
Testing H0: 32775 = 0b1000000000000111 (bit 4 = 0)
Testing H1: 32791 = 0b1000000000010111 (bit 4 = 1)
Actual bit value: 1
Measuring noisy wall-clock timings...
Prediction means: H0=8.803μs, H1=10.185μs
Error variances: H0=0.08, H1=0.09
Decision: bit = 0
Result: ✗ WRONG

--- Attempting bit 5 (LSB+5) ---
Testing H0: 32775 = 0b1000000000000111 (bit 5 = 0)
Testing H1: 32807 = 0b1000000000100111 (bit 5 = 1)
Actual bit value: 1
Measuring noisy wall-clock timings...
Prediction means: H0=10.007μs, H1=11.400μs
Error variances: H0=0.07, H1=0.08
Decision: bit = 0
Result: ✗ WRONG

============================================================
FINAL RESULTS
============================================================
Target key:     53 (0b110101)
Recovered key:  7 (0b111)
Accuracy: 3/6 bits correct (50.0%) (includes assumed LSB)

正如我们所看到的，攻击仅达到 50% 的准确率，这相当于随机猜测。请注意，在所有尝试中，误差 variances 几乎相同（0.11 vs 0.11、0.10 vs 0.09、0.09 vs 0.10），这使得 distinguisher 无法可靠地判断哪个假设是正确的。即使有 3000 条消息和 100 倍的放大倍数，信号仍然埋在噪声中。

这种失败说明了一个重要的教训：理论漏洞和实际开发可能完全不同。在第 1 部分中显得清晰的微秒 timing 差异被以相同微秒测量的系统噪声所淹没。现实世界的 timing attacks 需要比简单地 timing 算法执行更复杂的 measurement 技术。

Part 3: Engineering Solutions

我们能比第 2 部分做得更好吗？答案在于系统的工程设计，它可以解决每个variation来源。Python 的垃圾回收器引入timing spikes？在 timing 循环期间禁用它。CPU 缓存和分支预测器导致启动效应？添加预热运行。measurement 之间的系统漂移？交替测试假设的顺序。来自上下文切换的Outlier measurements？使用稳健的统计数据将其过滤掉。

以下是我们使用的一些技术来改进攻击：

import numpy as np
import random
import time
import gc

def iqr_filter(data, factor=1):
    if len(data) < 4:
        return data
    data = np.array(data)
    q1 = np.percentile(data, 25)
    q3 = np.percentile(data, 75)
    iqr = q3 - q1
    if iqr == 0:
        return data.tolist()
    lower = q1 - factor * iqr
    upper = q3 + factor * iqr
    filtered = data[(data >= lower) & (data <= upper)]
    if len(filtered) < len(data) * 0.5:
        lower = q1 - 3.0 * iqr
        upper = q3 + 3.0 * iqr
        filtered = data[(data >= lower) & (data <= upper)]
    return filtered.tolist()

def measure_timing_simple(operation, amplification=5000, num_runs=10):
    gc_was_enabled = gc.isenabled()
    gc.disable()
    try:
        times = []
        for _ in range(10):
            operation()
        for run in range(num_runs):
            if run > 0:
                time.sleep(0.001)
            start = time.perf_counter()
            for _ in range(amplification):
                operation()
            elapsed = time.perf_counter() - start
            times.append((elapsed * 1e6) / amplification)
        times_clean = iqr_filter(times)
        return np.median(times_clean)
    finally:
        if gc_was_enabled:
            gc.enable()

现在让我们针对与第 2 部分类似的目标测试我们的技术。我们将仍然使用随机的 512 模数，但这次我们将仅使用 1200 条消息而不是 3000 条消息。我们将使用更高的放大倍数 1000x，我们将重复 3 次以进一步消除噪声。最后，我们将 measurements 偏向于假设之间具有较大 delta 的 80% 的消息，以使辨别器的错误更加明显。为了使实验在我们的 Python 笔记本中运行相对较快，我们将假设密钥的前 7 位是已知的，我们将专注于恢复接下来的 3 位。

Part 3 Demonstration: Robust Timing Attack
============================================================
Target key: 2475 (0b100110101011)
Key length: 12 bits
Modulus: 512-bit prime modulus

🔧 Engineering Solutions:
• Drift-resistant measurements with order alternation
• Delta-based message filtering (top X% most discriminative)
• Original Kocher variance distinguisher
• Robust statistical analysis with IQR filtering
• Configurable bit start position

Kocher Attack
============================================================
Target key: 2475 (binary: 0b100110101011)
Messages: 1200
Amplification: 1000× × 3 runs
Filter percentile: 20%

Step 1: Generating test messages...
Generated 1200 messages

Step 2: Measuring baseline timings...
Complete! Mean: 23.91μs, Std: 0.51μs

Step 3: Attacking 3 bits starting from bit 8...
🔑 Assumption: bits 1 to 7 are known

--- Attacking bit 8 ---
Testing: H0=0b1000000010101011 vs H1=0b1000000110101011
Actual bit: 1
  Filtering: keeping 960/1200 messages with |delta| >= 1.315 (80% kept)
  Decision: bit = 1
  Prediction means: H0=17.397μs, H1=18.901μs
  Variances: H0=0.144770, H1=0.139724
  Delta stats: mean=1.449μs, std=0.164μs
  Result: ✅ CORRECT

--- Attacking bit 9 ---
Testing: H0=0b1000000110101011 vs H1=0b1000001110101011
Actual bit: 0
  Filtering: keeping 960/1200 messages with |delta| >= 1.328 (80% kept)
  Decision: bit = 0
  Prediction means: H0=20.156μs, H1=21.682μs
  Variances: H0=0.124010, H1=0.141704
  Delta stats: mean=1.465μs, std=0.181μs
  Result: ✅ CORRECT

--- Attacking bit 10 ---
Testing: H0=0b1000000110101011 vs H1=0b1000010110101011
Actual bit: 0
  Filtering: keeping 961/1200 messages with |delta| >= 1.347 (80% kept)
  Decision: bit = 0
  Prediction means: H0=21.482μs, H1=23.034μs
  Variances: H0=0.124903, H1=0.131268
  Delta stats: mean=1.492μs, std=0.181μs
  Result: ✅ CORRECT

我们的配置稳定吗？我们可以重复实验几次来估计它的可靠性。例如，成功运行两次已经大大降低了随机猜测的可能性，即 ((12)3)2=164。尽管如此，为了拥有更可靠的辨别器，我们可以进一步增加消息的数量和/或放大因子。请注意，消除尽可能多的噪声源，例如许多使用 CPU 的并发程序，确实可以提高信号的质量。

结论

这三幕之旅展示了密码分析如何从理论走向实践。在第 1 部分中，漏洞是清晰且易于利用的。在第 2 部分中，噪声和系统效应使其看起来遥不可及。在第 3 部分中，仔细的 measurement 和统计工程将理论重新转化为有效的攻击。

对于防御者来说，信息很明确： “学术”和 “实践”之间的差距通常只是工程方面的努力。如果存在 secret-dependent 分支或 timing variation，攻击者可能会通过足够的数据和谨慎来利用它们。最可靠的防御是完全消除泄漏，通过使用 constant-time implementations、blinding 和 side-channel-hardened cryptographic libraries。

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～