使用zkSPV合约的无需信任的比特币预言机
- Y9ehMW5MSySwzy3ercQYNw
- 发布于 2025-06-27 20:56
- 阅读 864
本文介绍了使用zkSPV合约实现无需信任的比特币预言机的概念和方法。文章讨论了SPV节点的设计,并提出了不同版本的SPV合约,包括如何利用SNARKs和递归证明来降低验证成本,以及如何处理区块头、Merkle树和交易验证。此外,还探讨了证明交易、比特币虚拟机、地址和UTXO集合等不同方面的应用。
使用 zkSPV 合约的无需信任的比特币 Oracle
如果你的链不与比特币交互,那你都在忙些什么呢?
如果需要在比特币和另一个系统之间构建跨链应用程序,则需要一种方法将比特币的历史记录与指定的网络同步。最直接的方法是使用 oracle(中心化的或联盟式的),但很少有人会认为这种方法是可靠的。同时,我们有明确的规则:(1)如何验证比特币区块和整个链的正确性;(2)如何检测主链,以及(3)在发生重组时该怎么做。我们可以用智能合约的形式编写比特币验证规则,允许每个用户提供区块,并在区块正确时接受它们。
我们可以用智能合约的形式实现一个完整的节点(它将验证所有区块和交易,管理重组和更新等),但存在维护成本的问题。幸运的是,Satoshi 提出了一个更轻量级的方法,称为 SPV 节点。
在这篇文章中,我们将描述 SPV 合约的概念以及实现它的方法。旅途愉快!
我们使用 Noir 构建了 Bitcoin prover(我们在文章中不断提到它)。我们还提到了一些我们应用的特定方法以及我们在框架和实现方面遇到的限制:https://github.com/distributed-lab/bitcoin-prover。我们恳请读者不要将自己局限于这个具体的提案,而是根据他们想要实现的需求和期望的属性来使用和应用他们喜欢的任何东西。很多工作仍在进行中;我们对任何想法和贡献持开放态度,所以这篇文章的这个版本肯定不是最新的。
回到 SPV 节点设计
SPV 节点概念最初在比特币白皮书中提出。它允许可靠地同步比特币历史,而无需维护完整的节点,只需同步区块头并验证它们的正确性。由于每个区块头都包含所包含交易的 Merkle 树根,因此可以可靠地证明这些交易。
对于交易验证,SPV 节点要求完整节点返回将此交易包含到区块中的证明。在这种情况下,Merkle 分支被用作证明。然后,SPV 节点执行一系列验证以确保交易有效。我们可以将这些验证列举如下:
- 区块头验证:
- 所有字段的结构和存在性:
version(4 字节)、prev_block(32 字节)、root(32 字节)、timestamp(4 字节)、bits(4 字节)、nonce(4 字节) - 区块是链的一部分,并且引用了现有的前一个区块
- 时间戳值超过了前 11 个区块的中值。根据他们的时钟,完整节点不会接受时间戳超过未来两个小时的区块。
- 难度目标 \(^1\)
- 包含 Header 所有先前部分的哈希值(双重 SHA256)与 nonce 值的连接必须等于区块哈希值(+ 满足难度目标参数)
\(^1\) 区块头双重哈希值必须满足定义的难度参数(必须小于目标值)。难度目标参数每 2016 个区块更改一次,以调整当前网络哈希率的区块挖掘时间。它通过将矿工挖掘过去 2,015 个区块所花费的总分钟数相加,然后将此数字除以协议期望的目标 20,160 分钟(2,016 个区块 x 10 分钟)来实现。然后将该比率乘以当前的难度级别,以产生新的难度级别。如果校正系数大于 4(或小于 1/4),则使用 4 或 1/4 代替,以防止更改过于突然。
- Merkle 分支验证。当 SPV 节点收到带有 Merkle 分支的交易时 – 它会验证该路径是否指向现有的 Merkle 树根(在主链区块头中定义)
- SPV 节点必须验证该区块是否包含在主链中(最重的链),这意味着在提供的区块之上构建了特定数量的区块。
我们将使用以下符号:
- \(\mathsf{bh\_verify}(h)\to \{0,1\}\) - 根据上面描述的规则验证区块头 \(h\) 的函数
- \(\mathsf{hbatch\_verify}(b_l,...,b_h) \to 0 /\{d,\mathsf{root}\)} - 验证从 \(h_l\) 到 \(h_h\) 的一系列 Header,如果正确,返回难度和 Merkle 树根的函数
- \(\pi_{\mathcal{R}}\) 是关系 \(\mathcal{R} = \{(a, b, c, ...; x, y, z,...): f(a, b, c, ..., x, y, z,...)\}\)的证明,其中 \(a\),\(b\),\(c\),… 是公共变量,\(x\),\(y\),\(z\),… 是私有变量。 为了证明这种关系,证明者将展示 \(x\),\(y\),\(z\),…的知识,以使 \(f(a, b, c, ..., x, y, z, ...)\) 为真
SPV 合约 v0
最直接的方法是将所有提到的验证都以智能合约的形式实现。在这种情况下,任何人都可以将比特币区块头提交给合约,只要它通过所有描述的验证。同时,任何人都可以使用合约的读取方法可靠地访问有关任何存储的区块头的信息,并保证其准确性。
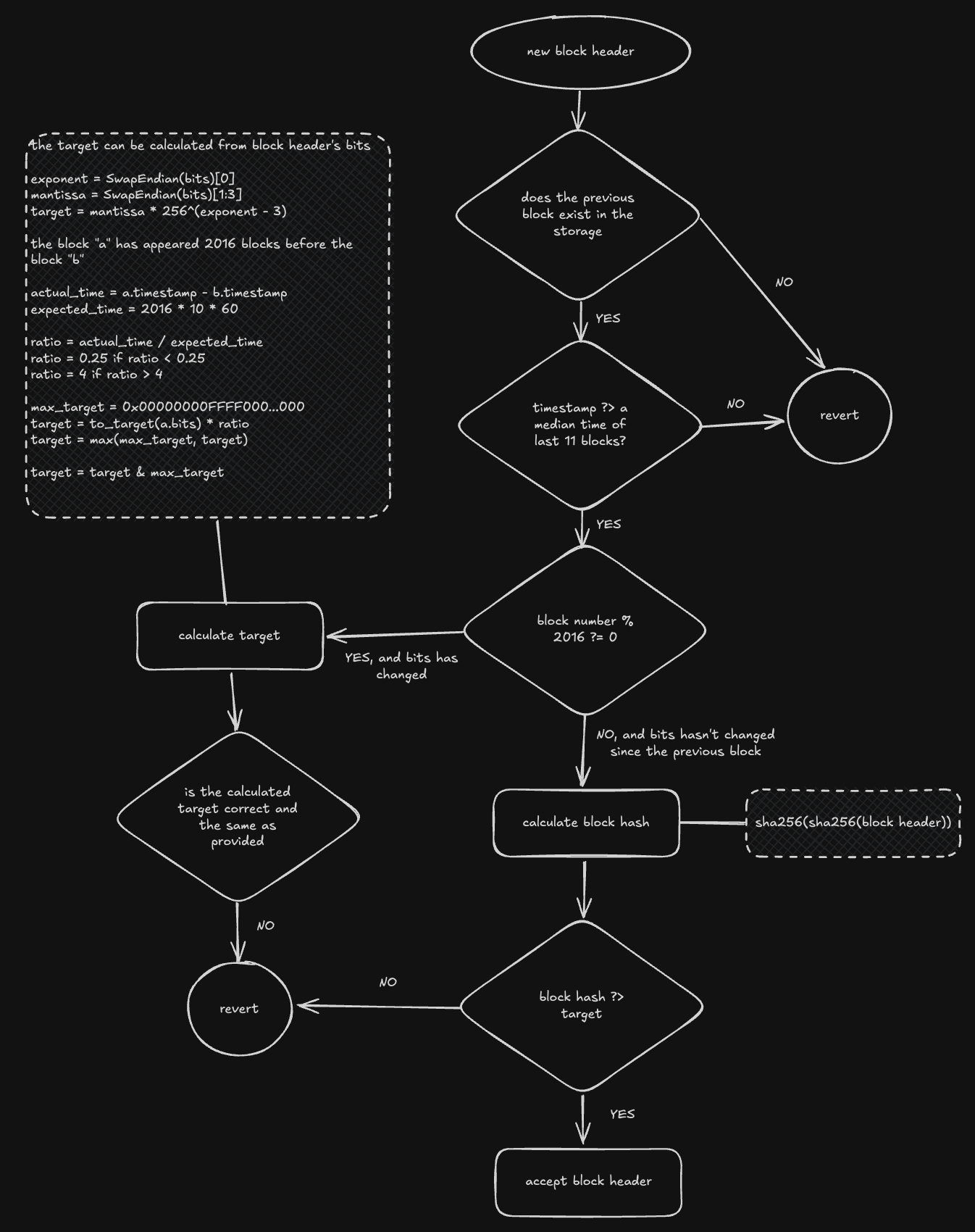
这里一个有趣的要点是标头验证的成本(基于你可以和 EIP 一起找到的参考实现 这里)。
让我们采用:
- ETH - $4400
- GasPrice - 2.5Gwei
=>
- 1 个区块头验证 ~ 130k gas => 0.000325 ETH = $1.43
不是很多,对吧?但是由于存在 915,000 个区块,因此同步整个比特币历史的价格为 $1.43 * 915,000 = $1,308,450。哎呀…
SPV 合约 v1
这实际上就是我们无法以这种形式启动 SPV 合约的原因。 好消息 – 我们有 SNARK。 因此,让我们将模型从“请验证整个历史记录”更改为“这是我知道截至某个检查点区块 \(N\) 的有效历史记录的证明; 请验证最新比特币区块之前的差异”。 在这种情况下,SPV 合约:
- 验证截至检查点的历史记录有效性的证明
- 验证所有区块头的 Merkle 树正确性的证明
- 验证最新区块头的批次
- 所有新区块都可以按照 SPV v0 逻辑逐个添加
成本? 假设我们正在证明 914,900 个区块并验证 100 个最新区块的批次:~$5 + 100 * $1.43 = $148。 便宜约 10,000 倍。
证明时间 (Noir + UltraHonk):109:53:24
Raito 在 6.5 小时内 使用 stwo 完成了它(这太棒了,尤其是我喜欢在 Raspberry Pi 上进行验证的可能性!)。 不幸的是,需要一个额外的带有 Groth16/PLONK/Ultragroth 的 SNARK 包装器才能使其在 Ethereum 上可验证。 这对于 SPV v1 假定的单次证明来说不是问题,但它与我们将稍后描述的 v2 不太兼容。
附:我们将使用 Binius 构建一个类似的 ZK 比特币客户端,它显示出令人难以置信的基准 – 例如,P2PKH + ECDSA 验证需要 175.89 毫秒来证明,在 Apple M2 Max 上需要 12.32 毫秒来验证证明。 现在唯一阻止我们的是没有递归(将在今年年底准备好)。
递归来了
我们无法对在一个周期中证明整个历史记录需要多少 RAM 进行基准测试。 一个粗略的估计是“很多”。 但是一种方法可能包括对历史记录进行分块,并以以下形式进行递归证明:
\[\mathcal{R}_i = \{(h_h, \mathsf{root}_i, d, \mathsf{pp}_i; \pi_{i-1},\vec{h}_i): \\ \mathsf{proofVerify}(\mathsf{pp}_i, \pi_{i-1}) \to 1 \land \mathsf{hbatch\_verify}(\vec{h_i})\to \{d,\mathsf{root}_i\}\},\]
其中 \(h_h\) 是上一个区块头,\(\mathsf{root}_i\) 是根据块中的 Header 构建的根,\(d\)– 结果难度,\(\mathsf{pp}\)– 公共参数(验证者的密钥等),\(\pi_{i-1}\)– 上一个递归的证明,\(\vec{h}_i\)– 块中的区块头。
实际上,由于正确的难度重新计算和基于块树构建全局根,因此该语句有点复杂。 但是我们不想让读者感到不知所措; 具体的逻辑始终可以在 这里 找到。
在实践中,你可以自由地使用 1024 个区块的块,而无需为了租用计算能力来证明而抵押你的房屋。
Merkle 森林
我们使用两层 Merkle 树结构来管理区块头。 第一层树 \(T^1_i\) 聚合一个块中的区块头。 第二层树 \(T^2\) 聚合所有 \(T^1\) 的根。
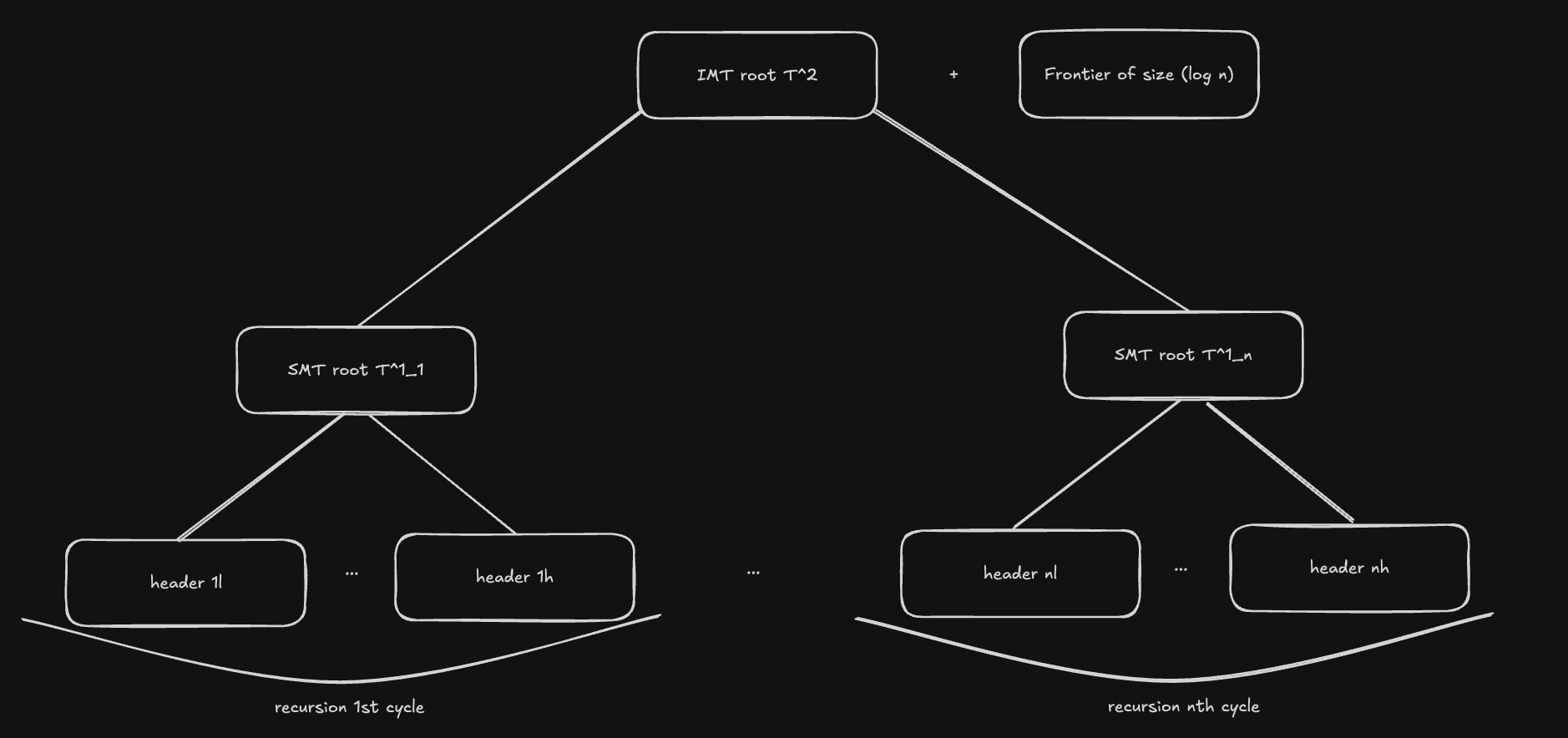
对于第一层树,我们使用 SMT 构造。 但是,从证明的角度来看,对全局树使用传统的 Merkle 树或 SMT 是低效的(由于需要在每个证明周期中重建全局树)。 相反,我们使用 增量 Merkle 树,它在证明周期之间传输边界,并允许我们以 \(O(\log n)\) 复杂度附加新的叶子。
SPV v1 合约部署在 这里:0x4c8D4e3C45870Df8b707c2dE9F2b3444971710F5
SPV 合约 v2
WIP
观察 #1. 我们真的需要在链上存储标头并管理重组吗? 如果我们可以将 SPV 合约简化为纯粹的 ZK 验证器,验证“我知道比特币主链,因为我知道根据比特币规则创建的最重链”这一说法呢?
在这种情况下,用户不会向 SPV 合约提供新的标头。 他们不会进行重组。 他们只是证明对比 SPV 合约上次已知的那条更长更重的链的了解。
观察 #2. 块可以等于 1 个区块。 这种方法使我们能够通过每个区块的递归来推广模型,证明“此区块是正确的,并且上一个区块的证明是正确的”这一说法。 因此,在这种情况下,(1)可以从任何高度到最新区块进一步证明标头链;(2)证明逻辑可以更加复杂,例如执行脚本,验证 UTXO 数据集等。
\[\mathcal{R}_i = \{(h_i, \mathsf{root}_i, d, \mathsf{pp}_i; \pi_{i-1}): \\ \mathsf{proofVerify}(\mathsf{pp}_i, \pi_{i-1}) \to 1 \land \mathsf{hb\_verify}({h_i})\to \{d,\mathsf{root}_i\} \land f_{ext}(\vec{\mathsf{tx}}, \vec{\mathsf{script}}, \vec{\mathsf{UTXO}}\to 1)\},\]
这导致了比特币主链追踪表:
| # | 证明 | 根 | UTXO 数据集 |
|---|---|---|---|
| … | … | … | … |
| \(n\) | \(\pi_{\mathcal{R}_n=\{\mathsf{proofVer}(\pi_{\mathcal{R}_{n-1}=\{...\}})\to1,\mathsf{b\_verify}(h_n)\to 1\}}\) | \(T^1_n,T^2\) | \(\mathsf{UTXO}_n\) |
| … | … | … | … |
可以看出,可以通过从任何高度执行适当的递归证明来实现重组。
还需要证明什么
除了 SPV 逻辑之外,比特币还有很多有趣的东西需要证明!
交易
TX 在我们的例子中是一个重要的结构。 它以原始十六进制字符串的形式进入系统,我们在 Noir 内部解析该字符串并创建一个相应的 TX 对象。 为了访问 TX 字段,我们对每个子对象(例如,任何输入)使用偏移量和大小:
- 输入: 每个输入都包含对先前交易输出
txid和vout的引用,以及一个sequence号。 输入存储为固定大小的数组,由编译时输入计数参数化 - 输出: 每个输出都包含一个
amount(8 字节)和一个可变长度的scriptPubKey。 与输入一样,输出也存储为一个在编译时确定大小的数组 - 见证数据: 对于 SegWit 交易,包含一个可选的 Witness 结构。 见证由堆栈大小和见证项目(通常是签名和赎回脚本)的集合组成。 这对于 SegWit 规则下的脚本验证至关重要
- 元数据: 其他字段包括
version、可选的 SegWitmarker和flag以及lock_time
所有交易参数,例如总大小、输入数量、输出数量和最大见证大小,都指定为编译时常量(全局参数)。 这允许 Noir 强制执行边界检查,而无需依赖运行时可变性,从而确保零知识环境中的确定性和安全性。
为了处理不同类型的比特币交易(例如 P2TR,P2MS,P2WPKH,P2SH-in-P2WSH 等),Noir 实现需要大量的编译时常量。 Noir 对变量定义和计算强制执行严格的规则,这些规则必须在编译时或编译时之前发生,这使得在电路本身内部动态计算这些参数变得不切实际。
为了解决这个问题,为每种交易类型(技术上,为每个新的证明)生成一个专用的
globals.nr文件。 该文件包含所有必要的与交易相关的常量,包括交易长度,脚本大小,见证数据大小和操作码计数。 这些值是针对要证明的特定交易量身定制的,从而确保了 ZK 电路中解析和签名验证的正确性。因为每个交易结构在长度、脚本格式和见证数据方面都有所不同,所以这些参数不能在交易类型之间共享。 相反,它们是通过 Python 生成器自动创建的,该生成器解析原始交易数据(包括当前和先前的交易)。 该生成器使用正确的常量填充预定义的 Noir 模板,生成最终的
.nr和.toml文件。 这种自动化避免了手动计算错误,并保证了电路可以在编译时访问所有必需的值。这种设计模式允许 Noir 保持灵活性和效率:证明电路保持通用,而特定于交易的常量则通过自动生成的全局文件注入。
比特币虚拟机
WIP
不要忘记 Simplicity 证明 =)
地址
比特币支持多种地址和锁定脚本类型,每种类型都定义了不同的支出条件和验证逻辑。 在我们的系统中,这些都表示为专用的 Noir 电路,其中对于每个受支持的地址类型,我们都会生成一个对应的 globals.nr 文件。 生成过程通过基于 Python 的生成器自动完成,该生成器根据正在验证的交易来构建适当的电路。
在当前阶段,我们支持大多数比特币地址和脚本类型:
| 地址 | 描述 |
|---|---|
| Pay-to-Multisig (P2MS) | 传统的 M-of-N 多重签名方案,将输出锁定到多个密钥。 该方案检查是否有足够的有效签名。 |
| Pay-to-PubKey (P2PK) | 最简单的传统类型,直接锁定到公钥。 该方案根据公钥检查签名。 |
| Pay-to-PubKey-Hash (P2PKH) | 传统类型,将输出锁定到公钥的哈希,需要签名和密钥才能花费。 关键的区别在于,我们已经链接了传统方案和 segwit 方案,并在一个方案中检查交易是否为 SegWit。 根据答案,我们从见证数据或 scriptSig 中获取签名和公钥。 |
| Pay-to-Script-Hash (P2SH) | 通过仅提交到其哈希值来封装任意赎回脚本。 关键的区别与之前的类型相同。 我们结合了传统方案和 segwit 方案,根据这一点,脚本的最后一个元素将是 redeemScript(传统)或 witness script(segwit) |
| P2SH 嵌套 SegWit (P2SH-in-P2WPKH) | SegWit v0 的兼容形式,将 Pay-to-Witness-PubKey-Hash 嵌入到 P2SH 信封中。 简单地执行位于 scriptPubKey 中的 redeemScript。 |
| P2SH 嵌套 SegWit (P2SH-in-P2WSH) | 与上述类似,但将 Pay-to-Witness-Script-Hash 嵌入到 P2SH 信封中。 与之前的类型相同,执行位于 scriptPubKey 中的 redeemScript |
| Pay-to-Taproot (P2TR, 密钥路径) | 基于 Schnorr 签名的原生 SegWit v1 地址类型,支持通过密钥路径进行单密钥消费。 该方案根据 BIP-341 规则验证 Schnorr 签名 |
| Pay-to-Taproot (P2TR, 脚本路径) | 使用 Merkle 提交的脚本的替代 Taproot 消费路径。 该方案首先验证调整后的密钥,然后执行脚本 |
实际上,我们对一项从 Project 11 派生的任务进行了一项有趣的实验。 这是一个用于 P2PKH 地址的客户端 ZK PQ 证明器。 这是基准:

\(^*\) 它不包括 Binius 基准,因为缺少 ZK,但将在今年年底准备就绪。
UTXO 集
WIP
案例
- Wrapless
- 储备证明
- 基于跨链订单的 DEX
- 原文链接: hackmd.io/Y9ehMW5MSySwzy...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 中本聪留给读者的习题 19 浏览
- AI智能体将推动比特币走得比人类独自更远 66 浏览
- 为比特币的量子抗性研究基于哈希函数的签名方案(四) 62 浏览
- 民主事物的再思考:构建共识发现工具 92 浏览
- Zero 链: 技术定位报告 182 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 188 浏览
- 以太坊 2029 Strawmap 傻瓜指南 246 浏览
- 不实的断言:攻破 6 个 zkVMs 175 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 323 浏览
- 零知识编年史:群 253 浏览
- 为比特币的量子抗性研究基于哈希函数的签名方案(一) 276 浏览
- 以太坊执行层优化:状态树与虚拟机 413 浏览

