ZK 编年史：数学基础

想要获得更具互动性的体验，请在我的个人博客 Arkana 上阅读本文。

在我们完成了本系列介绍之后，现在是时候开始构建我们的工具包了，这样我们就可以朝着制作我们已经提到过的这些证明系统的目标前进了。

我真诚地希望之前的文章不会太可怕。为了稍微弥补一下，我想说，我们今天要研究的概念并不是很复杂，同时对于任何严肃的密码学来说，都具有相当基础的额外好处。

如果我见过好的提议，这绝对算一个！

但是，需要提醒一句：当我们一起深入旅程时，我们将需要更多的工具。当然，我们会在适当的时候讨论它们 —— 但我只是不想让你认为这篇文章足以让你为余下的路程做好准备。

有了这些，上下文就清楚了！那么我们从哪里开始呢？

有限域

在密码学中，精度至关重要。

我的意思是，算法需要是一致的。试想一下，一种数字签名只有偶尔才起作用 —— 我想你会同意我的观点，这是一个（请原谅我的法语）糟糕的算法。

因此，我们的基本信息单元，或者说我们从现在开始表示事物的方式，必须能够避免操作中的小错误，否则这些错误可能会在未经检查的情况下爆炸。

如果我们在这里真的很挑剔，这并非绝对正确 —— 一些基于 learning with errors 问题的算法允许小错误，但由于它们是预期的，并且通过特殊技术进行了解释，因此仍然可以正常工作。

整数在这方面做得很好：通过避免 floating point 运算，我们可以保持事物的清洁和一致。因此，我们将要构建的最基本结构是一个 整数集合：我们称之为 有限域，这应该不足为奇。

严格来说，一个 field 被定义为一个 元素集合，对于这个集合，我们可以定义四种运算：加法、减法、乘法 和 除法（除以零或类似零的元素除外）。

这听起来应该很熟悉 —— 我们熟知和喜爱的 实数 就是一个域！

当我说“我们可以定义”时，我的意思是，我们有 明确的规则 来执行这四种运算，并且运算的结果 也必须是该域的一部分。也就是说，我们将集合想象成我们的可能性宇宙：对于我们来说，任何不属于该集合的东西根本 不存在。稍后你会更容易理解这一点。

我们有时需要添加一个额外的元素（到集合中）。这是一个有用但更高级的概念，称为 field extensions。

finite field 只是一个具有有限元素集合的域。像这样：

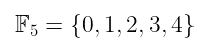
看完那个表达式后，脑海中应该立即浮现出一些问题。例如，2 + 3 = 5 不是集合的一部分。那么会发生什么呢？

这正是我之前所说的：加法 没有被很好地定义，所以我们必须“扩展”我们的域以包含新元素。其他操作也会发生类似的情况。

如果我们必须为每个可能的结果添加一个新元素，我们的集合就会无限增长！所以看来我们从一开始就陷入了一团糟……

不要烦恼，年轻人。我说这四种运算必须被定义，但我从未说过 如何！

你这个狡猾的混蛋

由于标准运算在这种情况下似乎不起作用，因此我们需要找出 其他方法 来定义加法、减法、乘法和除法。事实上，有 多种方法 可以做到这一点 —— 但有一种方法特别适合我们的需求。

模运算

我们所要做的就是使用标准运算，然后将结果传递给 modulo operation：

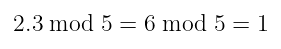
没什么太花哨的，对吧？

这是可行的，因为模运算将所有结果都转换为我们的原始集合，甚至是 负数。我们所需要做的就是取结果模 $p$，即域大小。在上面的例子中，这个数字当然是 5。

但仍然存在一个小问题：除法 怎么办？我们的有限域不允许有分数，因为我们一开始就没有 分数 的概念。

这需要一种视角的转变。你看，任何除法都可以用另一种方式来解释：乘以倒数。

一个简单的例子可以帮助你 이해：用 2 除 3（即 3 / 2）与将 3 乘以 0.5 完全相同。在本例中，0.5 是 2 的倒数 —— 我们可以将其写为 2⁻¹。

正如我之前提到的，倒数的概念在我们的上下文中没有意义，因为不允许有 分数。

但并非所有希望都破灭了 —— 我们可以从倒数中提取出一个特别的 见解，它将为我们提供解决这个问题的线索。具体来说，任何数字$a$（除了 0）及其倒数$a^{-1}$满足以下关系：

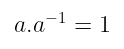
所以这里有一个想法：对于我们域中的每个元素$m$，是否可以找到某个数$m^{-1}$，当它与$m$（模$p$）相乘时，结果为$1$？

当然，不包括 0！

有趣的是，答案取决于$p$的值。如果存在这样的数字，则称其为$m$在$p$上的模逆，其存在的条件是$m$和$p$是互质。

互相什么？

互质数 只是用于描述 没有共同因子 的两个数字的 奇特名称 —— 也就是说，它们的最大公约数是 1。

这里有另一个巧妙的见解：当$p$本身是质数时，每个小于$p$的非负整数（除了 0）都 与它互质。换句话说，我们集合𝔽ₚ中的 所有元素 都将 有一个逆，这反过来意味着我们可以为整个集合定义除法。

有了这些，所有需要的运算都已定义，因此我们的有限域已准备就绪！

我们能用它们做什么？

多项式

嗯，实际上很多!

就我们的目的而言，也许我们可以做的最重要的事情是构建有限域上的 多项式 —— 正如我们稍后将看到的，多项式是现代证明系统背后的秘诀。

多项式是一个 表达式，它具有一个或多个 变量，并且只能涉及一些 简单的运算：加法、减法、乘法和指数运算（使用非负整数幂）。看起来可能像这样：

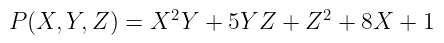
正如你所看到的，每一项都由变量的乘积（如果不是显式的，则只是 1）和另一个我们称之为 系数 的“普通”数字组成。同样，如果系数不是显式的，则意味着它的值是 1。

我们还需要定义多项式的 度：它是任何一项中 指数的最高和。在上面的例子中，项$X²Y$的度为 3（因为$2 + 1 = 3$），这是任何一项的最高度，因此$P$的度为 3。

早些时候，我提到多项式仅通过加法、减法和乘法来构建 —— 因此我们假设变量表示的值 允许 这些运算。也就是说，我们假设，例如，乘以$x \cdot y$是公平的。这是否让你想起了什么？

没错！这听起来很像 域，所以它们似乎与所有这些有关。而且可以肯定的是，多项式 必须在某个域上定义。

更重要的是，如果我们选择一个 有限域，这意味着我们只使用域元素作为系数，并且我们将变量值也限制为有限域，那么多项式的 输出 也将 属于该域。

在某个域 𝔽 上定义的多项式集合通常表示为 𝔽[X]。

这非常好。我们可以使用先前定义的有限域，几乎可以保持不变 —— 因此这看起来确实像是构建东西的沃土。

多项式有无数的应用。我们将主要将它们用作构建块，因为它们擅长两个领域：表示计算 和 编码信息。

我知道 —— 所有这些定义都感觉有点抽象。所以让我们通过更实际的角度来解决下一部分。

编码信息

我刚才声称多项式擅长编码信息 —— 但这怎么可能呢？毕竟，它们只是我们可以评估的表达式。这对编码有什么好处？

信不信由你，秘密在于一个意想不到的嫌疑人：系数。

让我们先关注单变量多项式。列出不同项的系数（假设从最高度到最低度）会得到一个 域元素的列表 —— 换句话说，就是整数向量。

暂时忘记多项式：整数向量可以代表几乎任何类型的信息！更重要的是，假设我们的域是 𝔽₂，因此我们只有 0 和 1 可用。这正是机器语言 —— 0 和 1 的字符串！

好的，这很酷… 但为什么不直接使用向量呢？我们将这些向量解释为多项式的唯一原因是有一些好处可以获得。事实上，确实有。

插值

我在 previous post 中谈到了这一点。我建议你查看一下，以获得更详尽的分步指南！

取 𝔽[ $X$] 中的一些多项式 $P(X)$。假设我们选择一些点 $x₁$、$x₂$ 等等，直到我们有 $n$ 个点（这样我们就可以到达 $xₙ$）。当我们在这些点评估多项式 $P(X)$ 时，我们只需得到一堆域元素 —— 每个不同的输入一个。

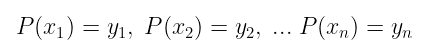
我们称这些对为 评估 或 P 的评估点。不过，术语有时会用得很松散，“评估”可能只指结果。

此外，请注意 表示法：变量用 大写字母 书写，而评估用 小写字母 书写。本系列的其余部分都将如此！

好的，酷，评估似乎很容易，所以这是一个更棘手的问题：我们可以 反过来 吗？

也就是说：给定一堆评估 (x₁, y₁) 到 (xₙ, yₙ)，你能找到 生成了所述点 的多项式吗？

是的，我们可以。这个过程称为插值（或拉格朗日插值），它 非常有用。只要我们注意一些细节。

让我们看看。一次多项式只是一条 直线：

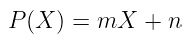
快速测验：你需要多少个 点 才能定义一条直线？

剧透区

我们需要 至少两个点。事实上，如果我们有更多的点，它们需要对齐，否则它们不会定义一条直线，而是其他函数。

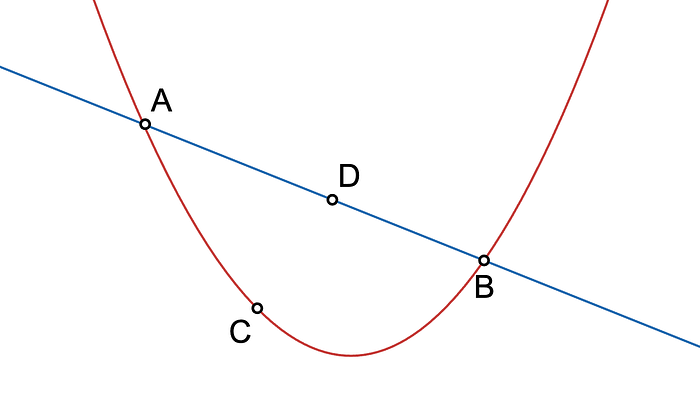
在前面的例子中，很明显，插值三个点会产生一个 至多 二次的多项式（一个抛物线），但如果这些点对齐，它也可能是一次多项式，如果它们垂直对齐，则可能是零次多项式。

这可以很好地推广到以下情况：

插值 N 个点会产生一个至多 N - 1 次的多项式

相反，我们需要至少 N 个点才能正确编码一个 $N - 1$ 次多项式。这具有以下惊人的含义：如果我们取任何 $N - 1$ 次的单变量多项式，我们可以通过在 N 个或更多个点对其求值来 编码它。然后，接收到这些 N 个（或更多个）点的任何人都可以通过插值重新计算原始多项式！

所以在某种程度上，拥有一堆多项式评估是表示某些多项式的另一种方式！

这都很好 —— 但是我们实际上该怎么插值呢？

拉格朗日多项式

虽然有更快的方法来做到这一点（通过 Fast Fourier Transform），但规范方法非常聪明，并且也提供了一些很好的见解。所以让我们看看它。

这个想法如下：假设我们有一组 N 个评估。对于其中一个，比如 (xᵢ, yᵢ)，我们可以构建一些 特殊 的多项式，它对于除了 $xᵢ$ 之外的所有 $x$ 值都将有一个 0 值，对于 $xᵢ$ 则恰好是 1 值。我们把这个多项式叫做 $Lᵢ(X)$。

这有点像是我们在数学上使用 Lᵢ(X)“选择”xᵢ。

我们为什么要这样做？这样想：如果我们把这样一个多项式乘以$yᵢ$，那么我们刚刚构造了一个小函数，使得：

因为 (xᵢ, yᵢ) 是原始多项式的 评估，所以我们希望从插值过程中得到的是一个多项式$L(X)$，使得对于我们所有的评估都有$L(xᵢ) = yᵢ$ —— 所以看起来$Lᵢ(X)$让我们完成了 一半。

为了得到我们的插值多项式，我们所需要做的就是把所有评估值的$Lᵢ$加起来：

瞧！这将会是我们插值的结果。从视觉上看：

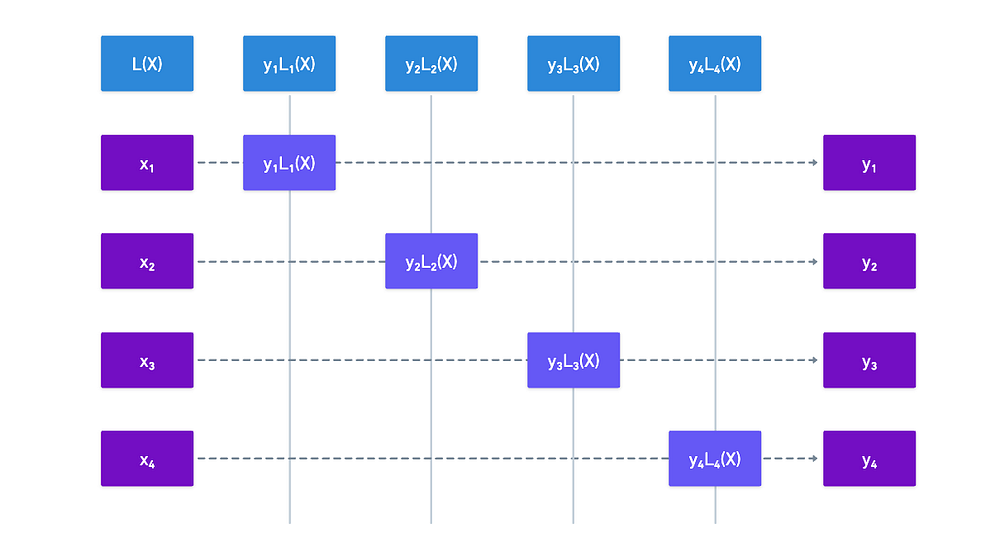
剩下要做的就是确定这些$Lᵢ(X)$是如何定义的，从而把所有东西很好地联系在一起。

根

让我们快速回顾一下我们的要求：每一个$Lᵢ(X)$在$xᵢ$上求值时都需要等于 1，在其他所有评估上等于 0。

一个多项式求值为 0 是一种特殊的事件。如此之多，以至于我们给这些值一个 特殊的名字：任何值$x$使得$P(x) = 0$，被称为多项式的 根。

尽管根表面上很简单，但它们非常强大。这其中的主要原因是存在一个重要的定理，称为 Fundamental Theorem of Algebra。

作为一般的经验法则，当你在数学中看到任何被称为“fundamental”的东西时，要知道这肯定是一些非常重要的东西。

稍微简化一下，这个定理最重要的结论之一是任何单变量多项式都可以表示为线性因子的乘积：

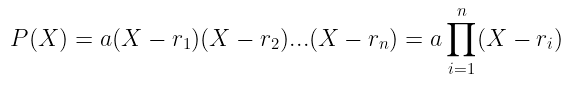
从这个表达式可以得出一个非常重要的观察结果：一个$N$次的多项式 至多有 N 个根。这是一个如此重要的引理，再重复一遍也无妨，以增加一些戏剧性色彩：

一个 N 次的多项式至多有 N 个根

这个事实非常重要，并且会产生我们所能支配的一些最强大的工具。我们现在将暂停一下，但要知道我们很快就会回到这一点。

现在，回到插值，事实证明这种形式非常有用。很明显，当我们评估任何一个$rᵢ$值时，我们会得到$P(rᵢ) = 0$。我们可以在这里利用这一点：$Lᵢ(X)$多项式在所有的$x$值上都需要是 0，除了 $xᵢ$，这意味着它们是$Lᵢ(X)$的根！因此，我们可以将$Lᵢ(X)$构造为：

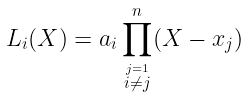
我们故意省略了 xᵢ，以便它 不是 结果多项式的根。

太棒了！我们现在唯一缺少的细节是调整$aᵢ$系数，以便我们精确得到$Lᵢ(X) = yᵢ$。对表达式进行简单的 归一化 即可：取在$xᵢ$处$Lᵢ(X)$产生的任何值，然后将整个表达式除以该值。这样，当评估$Lᵢ(xᵢ)$时，我们只需得到 1。

完整的表达式是：

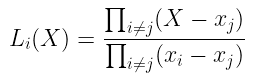
差不多就是这样了！

这组 Lᵢ(X) 被称为 拉格朗日基。我们稍后可能需要更深入地研究这个名称的含义，但就目前而言，该名称足以参考！

总结

好的！今天就到这里了。

我们现在拥有的东西可能看起来有点平淡无奇。我的意思是，我们所有的只是 数字 和 表达式 —— 这些东西可能感觉有点基础。

诚然，从我们到目前为止所见的这些相当简单的元素中，有很多复杂性需要剥离。但我认为，现在这样做既不实用也没有指导意义。

相反，最好开始探索利用这些概念的 应用。当我们开始使用这些工具时，它们的潜力将开始变得更加明显。

因此，在我们的 next encounter 中，我们将研究我们可以从今天提出的这些构建块中构建出的最简单但最基本的协议之一。

再见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～