深入探索范围：更深入地了解 Bulletproofs

我们之前已经了解了 Bulletproofs 内部乘积论证 (IPA) 的工作原理：它让我们能够证明我们知道一个秘密向量，而无需泄露它。

这很棒，但我们实际上可以用它做什么呢？

→ 范围证明！

Bulletproofs 是现代范围证明的支柱：它允许我们证明一个秘密值位于给定的范围内，而无需泄露该值本身。

如果你没有读过之前的 IPA 文章，请不要担心，你可以将 IPA 视为一个黑盒，它可以证明内部乘积关系，而无需暴露向量。不过……如果你确实想理解它，请阅读 分解 Bulletproofs（第一部分） 和 展开 Bulletproofs 的魔力（第二部分）。

这是我们今天要讨论内容的快速概览 😅

（此图表来自优秀的 Dalek Bulletproofs 文档）

不！🥲 不要在这里停下来！我保证，在本文结束时，这张看起来很奇怪的图表将变得完全有意义。

一个启发性的例子

一个很好的用例是 保密转账。

想象一下，你想给朋友汇款，但你不想让其他人看到汇款金额。你仍然需要证明转账是有意义的：你没有发送负数或超过你的余额。

在许多保护隐私的系统中（例如，当余额由同态承诺表示时），这需要证明金额和最终余额都保持在有效范围内，防止溢出/下溢，而无需泄露它们的实际值。

例如：

• 你可以转移的最大金额是 100
• 允许的最大余额是 1000

你将生成两个范围证明：

1. 转账金额有效： 0 ≤ amount ≤ 100

2. 最终余额有效： 0 ≤ balance - amount ≤ 1000

如果两者都成立，你的转账是正确的……而无需泄露实际数字。

这些类型的证明称为范围证明，而 Bulletproofs 是有效构建它们的一种方法。

也存在其他结构（例如，参见 2024 SoK 论文），但 Bulletproofs 仍然是当今最实用的结构之一。它们被门罗币 (Monero) 采用，以在生产中实现保密交易而闻名。

我们试图证明什么？

我们想要证明一个秘密值 $v$ 位于 $[0,2^n)$ 范围内，而无需泄露 $v$。

你可以将相同的逻辑应用于任何范围 $[a,b]$，但今天我将保持 2 的幂，这使得数学更简洁。

你可能已经猜到，我们将重用我们的向量机制和我们之前构建的内部乘积论证（需要复习吗？请查看 分解 Bulletproofs（第一部分） 和 展开 Bulletproofs 的魔力（第二部分） 😁）。

符号

每当我使用 粗体 时，这意味着我在谈论向量。

• $2^n = (2^0, 2^1, 2^2, ..., 2^{n-1})$

长度为 n 的向量，包含 2 的连续幂

• $0^n = (0, 0, ..., 0)$

n 个零的向量

• $1^n = (1, 1, ..., 1)$

n 个一的向量

• $y^n = (y^0, y^1, y^2, ..., y^{n-1})$

长度为 n 的向量，包含随机值 y 的连续幂

• $z1^n = (z, z, ..., z)$

向量 n 个元素，全部等于 z（按 z 缩放的 $1^n$）

将我们的秘密数字分解为位

Bulletproofs 范围证明中的关键技巧是位分解，即将一个秘密数字分解为它的各个位。

注意

这也与其他系统中使用的相同基本方法：你证明每个位要么是 0，要么是 1，并且它们的加权和重建该值。例如，在 Circom 中，这是通过 Num2Bits 小工具完成的。

虽然较新的证明系统有时使用 基于查找的范围检查 来提高效率，但位分解仍然是大多数协议所依赖的基本构建块。

我们将秘密值 $v$ 表示为其位的总和。

令 $a_L$ 为 $v$ 的位向量。

例如，如果 $v = 123 = 0b1111011$：

$a_L = (1, 1, 1, 1, 0, 1, 1)$

那么：

$\langle a_L, 2^n \rangle = v$

该内部乘积精确地表达了二进制数的工作方式：

$a{L0} \cdot 2^0 + a{L1} \cdot 2^1 + ... + a_{Ln-1} \cdot 2^{n-1} = v$

（注意：这里我假设 $a_L$ 是小端序）

使用我们的示例（以 大端序 形式）：

$1 \cdot 2^6 + 1 \cdot 2^5 + 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 64 + 32 + 16 + 8 + 2 + 1 = 123$

我们的范围证明将围绕说服验证者：

• 此等式成立，并且
• 每个 $a_{Li}$ 确实是一个 位（0 或 1）

这很重要，因为验证者只会看到对 $a_L$ 的 承诺，而不是向量本身。因此，如果没有此检查，证明者可能会将任意值隐藏在承诺中，并且仍然使等式平衡。

说服验证者我们的位是真实的 0 和 1

我们不能只是告诉验证者我们的位，那会泄露 $v$。

因此，我们需要一种方法来证明 $a_L$ 的每个分量要么是 0，要么是 1。

对于单个数字 $x$，作为一位意味着：

$x \cdot (x - 1) = 0$

只有当 $x$ 为 0 或 1 时，该等式才成立。

对于向量，我们使用元素乘法（哈达玛积）$\circ$：

$x \circ (x - 1^n) = 0^n$

因此，我们定义一个新的向量：

$a_R = a_L - 1^n$

我们想要证明：

$a_L \circ a_R = 0^n$

这确保了 $a_L$ 的所有条目都是二进制的。

注意

你可能想知道为什么我们在等式中引入一个新向量而不是直接使用 $a_L - 1^n$。

原因主要是结构性的：我们需要在证明的不同部分引用 $a_L$ 和 $a_R$，有时一起引用，有时单独引用。

通过将此表达式分配给它自己的变量，我们使后面的等式更简洁且更易于处理，尤其是当我们开始构建 涉及每个向量的内部乘积和承诺时。每个向量在证明中都扮演着不同的角色，并且显式定义它们可确保这些承诺与我们正在执行的约束保持一致。

你也可以将其视为一个电路，其中每个运算都会产生一个新变量，并且我们约束每个关系。

在伪代码中，它看起来像这样：

def range_proof_circuit(params, priv, pub):
    bitlen = params
    com_v = pub
    a_L, a_R, ... = priv
    assert com(sum(a_L * power_of_2)) == com_v
    assert a_R == a_L - vec_1
    assert a_L * a_R == vec_0

一个巧妙的概率技巧

我们如何证明两个隐藏向量相乘为零而不泄露它们？

我们从一个简单的直觉开始：假设你想证明一个秘密数字 $x$ 等于 0。

如果验证者给你一个随机值 $r$，你用

$x \cdot r = 0$

(我们假设你不能作弊，并且必须发送该乘积的实际结果)

来回应

那么，除非你（真的）幸运，否则这种情况成立的唯一方法是如果 $x = 0$。

我们将相同的想法应用于向量，但存在细微的差异......

用于内部乘积的 Schwartz–Zippel 引理

我们刚刚看到了随机挑战如何帮助检查单个值是否等于零。

在这里，我们实际上有 几个 我们希望同时成立的 等式（每个向量元素一个）：

$a_i \cdot b_i = 0 \forall i$

如果不是这种情况，则这些项可能会相互抵消。

例如，对于长度为 3 的向量，你可以有：

$a_0 \cdot b_0 = 6$ $a_1 \cdot b_1 = -4$ $a_2 \cdot b_2 = -2$

即使每一行都非零，它们的总和（内部乘积）也等于 0，这不是我们想要的。

为了避免这种情况，我们 为每一行添加随机性。

这样，即使你试图作弊，你也无法预测如何使这些项抵消。

验证者发送一个长度为 $n$ 的随机向量 $r$，证明者现在必须证明：

$\langle a_L \circ a_R, r \rangle = 0$

为什么这行得通？

因为 $r$ 中的随机系数充当每个项的独立缩放，因此任何潜在的抵消都变得基本上不可能。

如果此等式对于随机挑战 $r$ 成立，则元素乘积本身极有可能全部为零。

形式上，这依赖于 Schwartz–Zippel 引理：我们将左侧视为一个多项式，并测试它在随机点处是否求值为零。如果确实如此，则很可能整个多项式恒等于零，并且被愚弄的概率最多为 $d/|F|$。

为了减少通信，验证者不发送整个向量 $r$，而只发送一个随机值 $y$。

然后，证明者构造 $r = y^n = (1, y, y^2, ..., y^{n-1})$

$a_R$ 格式正确

我们还有一个问题……我们还需要证明 $a_R$ 是诚实定义的：

$a_R \stackrel{?}{=} a_L - 1^n$

简单！我们通过证明另一个内部乘积等于零来做到这一点：

$\langle a_L - 1^n - a_R, y^n \rangle = 0$

同样，由于验证者随机选择 $y$，因此证明者无法伪造它。

总结：我们必须证明的一切

总而言之，证明者需要证明三个关系，每个关系都简化为一个内部乘积，可以使用 IPA 验证：

$\langle a_L, 2^n \rangle = v$ $\langle a_L - 1^n - a_R, y^n \rangle = 0$ $\langle a_L, a_R \circ y^n \rangle = 0$

请注意，我稍微重新排列了第三个等式。

它等效于我们之前的内容：

$\langle a_L \circ a_R, y^n \rangle = 0$

但是现在等式的结构与 Bulletproofs 承诺稍后表达的方式更好地对齐。

这就是我们的全部设置！从这里开始，我们将继续进行将所有内容联系在一起的更重的代数运算。

组合内部乘积

到目前为止，我们有 三个独立的内部乘积 需要证明。

这有点难以处理。

理想情况下，我们希望将它们捆绑到 一个可以被单个 IPA 证明的内部乘积 中。

为此，我们从验证者那里引入了另一个随机挑战：$z$。

然后，我们使用 $z$ 的幂对三个等式进行 随机线性组合：

$z^2 \cdot \langle a_L, 2^n \rangle + z \cdot \langle a_L - 1^n - a_R, y^n \rangle + \langle a_L, a_R \circ y^n \rangle = z^2 \cdot v$

这样，证明者无法独立地“调整”每个等式来作弊。一切都必须在组合中保持一致。

我们现在想要重新排列此等式，以便：

• 内部乘积的左侧仅是 $a_L$ 的函数
• 右侧仅取决于 $a_R$
• 结果仅取决于 $v$ 和验证者已知的常量

这种干净的分离将使稍后 承诺 每侧独立变得更加容易。

首先展开：

$z^2 \cdot \langle a_L, 2^n \rangle + z \cdot \langle a_L, y^n \rangle - z \cdot \langle a_R, y^n \rangle - z \cdot \langle 1^n, y^n \rangle + \langle a_L, a_R \circ y^n \rangle = z^2 \cdot v$

然后将 $-z \cdot \langle a_R, y^n \rangle$ 移动到另一侧，并将 $z$ 移动到内部乘积中：

$z^2 \cdot \langle a_L, 2^n \rangle + z \cdot \langle a_L, y^n \rangle - z \cdot \langle 1^n, a_R \circ y^n \rangle + \langle a_L, a_R \circ y^n \rangle = z^2 \cdot v + z \cdot \langle 1^n, y^n \rangle$ $\langle a_L, z^2 \cdot 2^n \rangle + \langle a_L, z \cdot y^n \rangle + \langle -z1^n, a_R \circ y^n \rangle + \langle a_L, a_R \circ y^n \rangle = z^2 \cdot v + z \cdot \langle 1^n, y^n \rangle$

最后按 $a_L$ 和 $a_R \circ y^n$ 分组

$\langle a_L, z^2 \cdot 2^n + z \cdot y^n + a_R \circ y^n \rangle + \langle -z1^n, a_R \circ y^n \rangle = z^2 \cdot v + z \cdot \langle 1^n, y^n \rangle$

现在将相同的项添加到两侧：

$\langle -z1^n, z^2 \cdot 2^n + z \cdot y^n \rangle$

简化后，我们得到：

$\langle a_L, z^2 \cdot 2^n + z \cdot y^n + a_R \circ y^n \rangle + \langle -z1^n, z^2 \cdot 2^n + z \cdot y^n + a_R \circ y^n \rangle = z^2 \cdot v + z \cdot \langle 1^n, y^n \rangle - \langle z1^n, z^2 \cdot 2^n + z \cdot y^n \rangle$ $\langle a_L - z1^n, z^2 \cdot 2^n + z \cdot y^n + a_R \circ y^n \rangle = z^2 \cdot v + (z - z^2) \cdot \langle 1^n, y^n \rangle - z^3 \cdot \langle 1^n, 2^n \rangle$

右侧的每一项（除了 $v$）都为验证者所知，因此我们可以将它们分组为一个已知的单个值 $\delta(y, z)$，该值仅取决于随机挑战：

$\delta(y, z) = (z - z^2) \cdot \langle 1^n, y^n \rangle - z^3 \cdot \langle 1^n, 2^n \rangle$

有了这个，我们终于得到了我们将继续使用的单个内部乘积：

$\langle a_L - z1^n, y^n \circ (a_R + z1^n) + z^2 \cdot 2^n \rangle = z^2 \cdot v + \delta(y, z)$

我们现在 将所有三个约束组合为一个 紧凑的内部乘积。

随机挑战 $z$ 将它们联系在一起，因此证明者无法有选择地满足一个而不满足另一个。

此等式是下一步中我们将使用的确切形式，届时我们将盲化并承诺向量。

SageMath 设置

在继续之前，让我们添加一些代码。

从现在开始，我将使用简短的 SageMath 代码片段来说明证明的每个步骤。

我们将在一个微小的玩具字段中进行操作，以保持计算简单（实际系统使用大型 256 位字段）。

具体来说，我们将使用：

• 素数域 F929
• 该字段上的椭圆曲线：$y^2 = x^3 + 5x + 15$，它具有素数阶 919

p = 929
Fp = GF(p)
E = EllipticCurve(Fp, [5, 15])
Fr = GF(E.gens()[0].order())

目标是检查 $v$ 是否为 8 位

$v \in [0, 2^8)$

我们定义向量：

• $1^n$
• $2^n$

然后将 $v$ 分解为位以形成 $a_L$ 和 $a_R$

n = 8  # 位数
print(f"We will be proving that v is between 0 and {pow(2, n)}\n")

## (2^0, 2^1, 2^2, ..., 2^(n-1))
vec_2n = vector([Fr(2 ^ i) for i in range(n)])
## (1, 1, 1, ..., 1)
vec_1n = vector([Fr(1)] * n)

v = Fr(random.randint(0, pow(2, n)))
print("v =", v)

v_bin = bin(v)[2:].zfill(n)[::-1][:n]
print("v_bin = ", v_bin)

aL = vector([Fr(int(bit)) for bit in v_bin])
assert v == sum([aL[i] * 2 ^ i for i in range(n)])

assert v == inner_product(aL, vec_2n)

## Define aR
aR = aL - vec_1n
assert inner_product(aL, aR) == 0

print("aL = ", aL)
print("aR = ", aR)

这与我们之前的等式匹配：

$v = \langle a_L, 2^n \rangle$

核心证明（没有零知识）

如果我们在这里停止，我们已经可以在我们组合的内部乘积上运行 内部乘积论证 (IPA) 并获得有效的证明，就像在上一篇文章中一样😊。

但是有一个问题：IPA 没有隐藏。它会泄露有关见证的信息，可能会泄露秘密值 $v$。

在实际协议中，我们将使用盲向量 $s_L, s_R$ 解决此问题。

在到达那里之前，让我们去掉东西，看看一个简化的版本在没有任何盲化的工作方式。

我们从先前组合的关系开始，并命名内部乘积的这两个方面：

$l = a_L - z1^n$ $r = y^n \circ (a_R + z1^n) + z^2 \cdot 2^n$

一个完全幼稚的协议会让证明者仅发送 $(l, r)$ 并证明

$\langle l, r \rangle = z^2 \cdot v + \delta(y, z)$

但这既不具有约束力也不私密。任何人都可以伪造满足等式的向量。

因此，我们添加承诺。

承认

在协议开始时（在知道 $y, z$ 之前），证明者承诺位向量和值 $v$：

$A = \langle a_L, G \rangle + \langle a_R, H \rangle + \alpha \cdot H$ $V = v \cdot G + \gamma \cdot H$

这里：

• $G$ 和 $H$ 是椭圆曲线生成器的向量（$a_L$ 的每个位一个）
• $G, H$ 是单个生成器，用于标量承诺
• $\alpha, \gamma$ 是用于隐藏的随机标量（盲化因子）

## Define generators
G = E.random_point()
H = E.random_point()

Gs = [E.random_point() for _ in range(n)]
Hs = [E.random_point() for _ in range(n)]

## Commit to v
print("\nWe can commit to v from the start")
blinding_gamma = Fr.random_element()
V = v * G + blinding_gamma * H
print(f"v commitment (V): {V}\n")

blinding_alpha = Fr.random_element()
A = inner_product(aL, Gs) + inner_product(aR, Hs) + blinding_alpha * H
print("A = ", A)
print("\nProver sends A, V to Verifier")

然后验证者发送质询 $y, z$

print("Verifier sends random challenges y and z\n")
y = Fr.random_element()
vec_y_n = vector([y ^ i for i in range(n)])

z = Fr.random_element()
vec_z_1n = vector([z] * n)

因此，我们现在可以定义我们的主要关系 $\langle l, r \rangle = z^2 \cdot v + \delta(y, z)$

l = aL - vec_z_1n
r = aR.pairwise_product(vec_y_n) + vec_y_n * z + z ^ 2 * vec_2n
main_inner_product = inner_product(l, r)

delta_y_z = (z - z ^ 2) * inner_product(vec_1n, vec_y_n) - z ^ 3 * inner_product(vec_1n, vec_2n)
t = z ^ 2 * v + delta_y_z

assert main_inner_product == t
print("Combined inner product = z ^ 2 * v + delta_y_z.\nWe can continue...\n")

重新缩放生成器：$H'$

先前的承诺是在协议开始时计算出来的，在收到验证者的任何质询之前。

因此，一旦验证者发送质询 $y, z$，我们就会面临一个微妙的问题：$r$ 包含 $y$ 的幂，但是 $A$ 是在 之前 $y$ 知道被创建的。

内部乘积中 $a_R$ 的每个坐标都乘以 $y^i$，但承诺 $A$ 是使用普通的 $H$ 做出的。我们需要协调这些。

诀窍是将 $y^i$ 因子吸收到基数中。这就是我们定义新向量的原因：

$H' = \frac{1}{y^n} \circ H$

此重新缩放确保对于任何向量 $u$：

$\langle y^n \circ u, H' \rangle = \sum_i (y^i \cdot u_i) \cdot (\frac{H_i}{y^i}) = \sum_i u_i \cdot H_i = \langle u, H \rangle$

换句话说，我们可以自由地将 $y^i$ 权重从向量侧“移动”到生成器侧，而不会改变承诺。

vec_y_n_inv = vec_y_n.apply_map(lambda x: 1/x)
H_y_minus1 = [vec_y_n_inv[i] * Hs[i] for i in range(n)]

构建点 $P$

有了这个，证明者构造一个椭圆曲线点：

$P = \langle l, G \rangle + \langle r, H' \rangle$

使用公共信息，验证者可以用早期承诺 $A, V$ 表示 $P$：

$P \stackrel{?}{=} A - \langle z1^n, G \rangle + \langle z \cdot y^n + z^2 \cdot 2^n, H' \rangle - \alpha \cdot H$

让我明确地向你展示这个相等：

$P = A - \langle z1^n, G \rangle + \langle z \cdot y^n + z^2 \cdot 2^n, H' \rangle - \alpha \cdot H = \langle a_L, G \rangle + \langle a_R, H \rangle + \alpha \cdot H - \langle z1^n, G \rangle + \langle z \cdot y^n + z^2 \cdot 2^n, H' \rangle - \alpha \cdot H = \langle a_L, G \rangle - \langle z1^n, G \rangle + \langle a_R, H \rangle + \langle z \cdot y^n + z^2 \cdot 2^n, H' \rangle = \langle a_L - z1^n, G \rangle + \langle a_R \circ y^n, H' \rangle + \langle z \cdot y^n + z^2 \cdot 2^n, H' \rangle = \langle l, G \rangle + \langle a_R \circ y^n + z \cdot y^n + z^2 \cdot 2^n, H' \rangle = \langle l, G \rangle + \langle r, H' \rangle$

完美！$P$ 的两种表示形式匹配。

P = A - inner_product(vec_z_1n, Gs) + inner_product(z * vec_y_n + z ^ 2 * vec_2n, H_y_minus1) - blinding_alpha * H
assert P == inner_product(l, Gs) + inner_product(r, H_y_minus1)

内部乘积论证

最后，验证者需要根据他拥有的值：$A, V$，挑战以及公共参数，检查 $P$ 是否正确构造。

为什么它可行？既然我们了解 $H'$，就很容易了：

IPA

最后，证明者运行一个 IPA 与基数 $G, H', Q$ 以证明：

$P + t \cdot Q = \langle l, G \rangle + \langle r, H' \rangle + t \cdot Q$

哪里：

• $Q$ 是验证者选择的另一个椭圆曲线生成器
• $t = z^2 \cdot v + \delta(y, z)$

验证者：

1. 通过上述公式从 $A, V, y, z$ 重建 $P$

2. 验证 $\langle l, r \rangle = t$ 的 IPA 证明

就是这样！一个 完全可靠但非零知识 的范围证明。

print("\nFinally we run the IPA with: P + t * Q")
Q = E.random_point()

ipa_proof = ipa(l, r, Gs, H_y_minus1, t, Q, Fr)
P_full = P + t * Q
verify(Gs, H_y_minus1, P_full, ipa_proof[0], ipa_proof[1], ipa_proof[2], ipa_proof[3], ipa_proof[4], Q, n, Fr)
print("IPA proof ✅")

要检查 ipa() 函数的代码，请参见此处：ipa.sage

对于我们简化协议的完整脚本：range-proof-simple.sage

真正的 Bulletproof 添加了缺少的盲化多项式以使其私有。但是在结构上，这已经是协议的核心。

从现在开始，一切都与隐私有关……🙈

用于零知识的盲化：向量到多项式

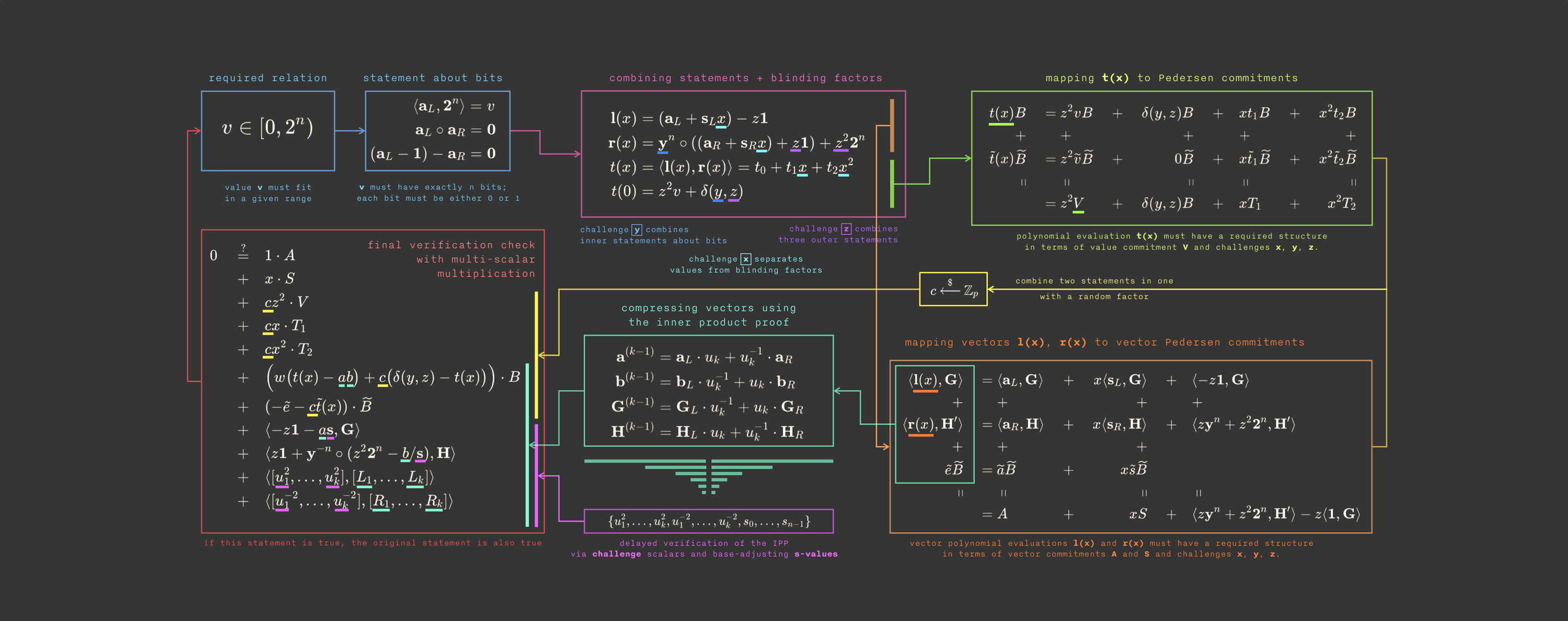
到目前为止，我们已经将我们的三个内部乘积组合为一个方程，并且看到了协议的非零知识版本。

为了使证明为零知识，我们需要隐藏这些向量，同时仍然说服验证者关系成立。

诀窍是双重的：

• 引入盲化因子以掩盖 $a_L, a_R$
• 并从向量转移到多项式，因此我们可以在单个结构化方程中组合真实数据和盲化项。

让我们看看证明者如何构建这些盲化多项式并使用 Pedersen 承诺对它们进行承诺，在保持每个方程可验证的同时隐藏所有秘密。

使用盲化术语隐藏我们的向量

证明者引入两个新的随机向量：$s_L, s_R$。

它们充当噪声以掩盖真实向量：$a_L, a_R$。

使用它们，我们定义两个取决于变量 $X$ 的多项式向量：

$l(X) = (a_L + s_L \cdot X) - z1^n$ $r(X) = y^n \circ ((a_R + s_R \cdot X) + z1^n) + z^2 \cdot 2^n$

当 $x = 0$ 时，这些多项式揭示了我们关心的原始表达式：

$l(0) = a_L - z1^n$ $r(0) = y^n \circ (a_R + z1^n) + z^2 \cdot 2^n$

现在看看当我们采用它们的内部乘积时会发生什么： $\langle l(0), r(0) \rangle = \langle a_L - z1^n, y^n \circ (a_R + z1^n) + z^2 \cdot 2^n \rangle = z^2 \cdot v + \delta(y, z)$

这是我们最终想要证明的核心公式。

通过将向量转换为多项式，证明者现在可以安全地在一个随机点（由验证者选择）揭示 $l(X), r(X)$，而不是揭示完整的秘密向量。

求它们的内积

当我们求两个多项式向量的内积时会发生什么？

如果我们有：$ax + b$ 和 $cx + d$，那么：

$\langle ax + b, cx + d \rangle = \langle a, c \rangle x^2 + (\langle a, d \rangle + \langle b, c \rangle) x + \langle b, d \rangle$

换句话说，结果是一个二次多项式。

在我们的例子中，我们称这个多项式为 $t(X)$：

$t(X) = \langle l(X), r(X) \rangle = t_0 + t_1 \cdot X + t_2 \cdot X^2$

常数项 $t_0$ 正是我们的目标内积：

$t_0 = \langle l(0), r(0) \rangle = \langle a_L - z1^n, y^n \circ (a_R + z1^n) + z^2 \cdot 2^n \rangle = z^2 \cdot v + \delta(y, z)$

注意

为了有效地计算剩余系数 $t_1, t_2$，我们可以使用一个简单的 Karatsuba 技巧：

$t_2 = \langle s_L, s_R \rangle$ $t_1 = \langle l(0) + s_L, r(0) + s_R \rangle - t_0 - t_2$

这节省了一些冗余的工作：我们没有逐项展开所有内容，而是重用现有部分来推导出交叉项 $t_1$。

所以从现在开始，我们的目标是：

• 证明 $t_0$ 是正确的：它等于 $z^2 \cdot v + \delta(y, z)$
• 证明 $t(X)$ 形式良好：
  • $l(X)$ 和 $r(X)$ 的构造是正确的
  • $t(X) = \langle l(X), r(X) \rangle$

对所有内容进行承诺

在验证者可以检查任何内容之前，证明者必须对所有相关值进行承诺。以一种具有约束力的方式（他以后不能更改它们），但仍然是隐藏的（验证者一无所获）。

这些承诺是对椭圆曲线点做出的，并遵循严格的顺序。

当我们之前描述“简化协议”时，我们已经看到了很多，但再次提醒一下也无妨。

步骤 1：承诺秘密值 $v$

使用随机的 blinding factor $\gamma$：

$V = v \cdot G + \gamma \cdot H$

其中 $G$ 和 $H$ 是固定的、独立的椭圆曲线生成元。

步骤 2：承诺到比特向量

现在，证明者承诺到向量 $a_L$ 和 $a_R$，以及 blinding 向量 $s_L$ 和 $s_R$：

$A = \langle a_L, G \rangle + \langle a_R, H \rangle + \alpha \cdot H$ $S = \langle s_L, G \rangle + \langle s_R, H \rangle + \rho \cdot H$

其中：

• $G$ 和 $H$ 是椭圆曲线生成元的向量（$a_L$ 的每个比特一个）
• $\alpha, \rho$ 是 blinding 标量

blinding_alpha = Fr.random_element()

A = inner_product(aL, Gs) + inner_product(aR, Hs) + blinding_alpha * H
print("A = ", A)

## blinding terms for left and right polys
sL = vector([Fr.random_element() for i in range(n)])
sR = vector([Fr.random_element() for i in range(n)])

blinding_beta = Fr.random_element()
S = inner_product(sL, Gs) + inner_product(sR, Hs) + blinding_beta * H
print("S = ", S)
print("\nProver sends A, S, V to Verifier")

一旦 A 和 S 被承诺，验证者（或 Fiat-Shamir 启发式）可以生成挑战 y 和 z。

这些然后用于定义 l(X),r(X) 和 t(X)。

R.<X> = Fr[]

lX = aL - vec_z_1n + sL * X
print("lX = ", lX)
rX = vec_y_n.pairwise_product(aR + vec_z_1n) + z ^ 2 * vec_2n + vec_y_n.pairwise_product(sR * X)
print("rX = ", rX)

tX = inner_product(lX, rX)
print(f"tX = {tX}\n")

步骤 3：承诺到 t(X)

最后，证明者承诺到 t(X) 的系数：线性项和二次项 t1 和 t2，每个都有自己的 blinding factor τ1,τ2：

$T1 = t1 \cdot G + \tau1 \cdot H$ $T2 = t2 \cdot G + \tau2 \cdot H$

这些承诺确保证明者以后不能调整 t(X) 使等式神奇地成立。

[t0, t1, t2] = tX.coefficients(sparse=False)

print("Notice that t0 is the inner product we're trying to prove\n")
assert t0 == main_inner_product

blinding_tau1 = Fr(123)
blinding_tau2 = Fr(456)
T1 = t1 * G + blinding_tau1 * H
T2 = t2 * G + blinding_tau2 * H
print("T1 = ", T1)
print("T2 = ", T2)

把它放在一起：验证

一切都快准备好了！🤩

证明者已经承诺了所有正确的片段。现在验证者只需要检查一切是否对齐。

最后的挑战

验证者发送最后一个随机挑战 x。

通过在这个随机点评估多项式 l(x),r(x) 和 t(x)，我们可以检查所声称的关系是否以压倒性的概率成立（感谢 Schwartz–Zippel 引理）。

证明者计算：

$l = l(x)$ $r = r(x)$ $\hat{t} = \langle l, r \rangle$ $\tau_x = \tau_2 \cdot x^2 + \tau_1 \cdot x + z^2 \cdot \gamma$ $\mu = \alpha + \rho \cdot x$

这里：

• $\hat{t}$ 是 t(X) 在 x 处的评估，等于 l 和 r 的内积
• $\tau_x$ 组合了 t(x) 的所有 blinding factors
• μ 组合了 A 和 S 的 blinding factors

print("\nVerifier sends challenge x\n")
x = Fr.random_element()
print("x = ", x)

## evaluate left and right polys at u
lx = lX(x)
rx = rX(x)
tx = tX(x)
print("lx = ", lx)
print("rx = ", rx)
print("tx = ", tx)
assert tx == lx * rx

print("\nProver sends proof_blindings_mu and proof_blindings_tau to Verifier")
proof_blindings_mu = blinding_alpha + blinding_beta * x
proof_blindings_tau = z ^ 2 * blinding_gamma + blinding_tau1 * x + blinding_tau2 * x ^ 2

验证者检查 #1：多项式 t(x)

首先，验证者确保 $\hat{t}$ 与所声明的多项式评估 t(x) 匹配。

从概念上讲，它检查的是：

$\hat{t} =? \langle l, r \rangle$

并且对 t(x) 的承诺与所有先前的承诺一致。

实际检查是：

$\hat{t} \cdot G + \tau_x \cdot H =? z^2 \cdot V + \delta(y,z) \cdot G + T1 \cdot x + T2 \cdot x^2$

为什么会这样？

$t(x) \cdot G = (t0 + t1x + t2x^2) \cdot G$ $t(x) \cdot G = (z^2 \cdot v + \delta(y,z)) \cdot G + t1x \cdot G + t2x^2 \cdot G$ $t(x) \cdot G = z^2 \cdot v \cdot G + \delta(y,z) \cdot G + x(T1 - \tau1 \cdot H) + x^2(T2 - \tau2 \cdot H)$ $t(x) \cdot G = z^2 \cdot v \cdot G + \delta(y,z) \cdot G + T1x - \tau1x \cdot H + T2x^2 - \tau2x^2 \cdot H$ $t(x) \cdot G + (\tau1x + \tau2x^2) \cdot H = z^2 \cdot (V - \gamma \cdot H) + \delta(y,z) \cdot G + T1x + T2x^2$ $t(x) \cdot G + (\tau1x + \tau2x^2) \cdot H = z^2 \cdot V - z^2 \cdot \gamma \cdot H + \delta(y,z) \cdot G + T1x + T2x^2$ $t(x) \cdot G + (\tau1x + \tau2x^2 + z^2 \cdot \gamma) \cdot H = z^2 \cdot V + \delta(y,z) \cdot G + T1x + T2x^2$ $t(x) \cdot G + \tau_x \cdot H = z^2 \cdot V + \delta(y,z) \cdot G + T1x + T2x^2$

check1_lhs = tx * G + proof_blindings_tau * H
check1_rhs = V * z ^ 2 + delta_y_z * G + T1 * x + T2 * x ^ 2
assert check1_lhs == check1_rhs
print("Check 1 ✅")

验证者检查 #2：向量 l 和 r

接下来，验证者检查所揭示的向量 l 和 r 是否与所有先前的承诺一致。

我们之前已经解释了 H′ 是什么。但为了方便懒人，这里再来一遍：

$H' = \frac{1}{y^n} \circ H$

然后它计算：

$P = A + x \cdot S - \langle z \cdot 1_n, G \rangle + \langle z \cdot y^n + z^2 \cdot 2_n, H' \rangle$

并检查：

$P =? \langle l, G \rangle + \langle r, H' \rangle + \mu \cdot H$

如果此等式成立，则意味着证明者的 l(x) 和 r(x) 构建正确。

P = - proof_blindings_mu * H + A + S*x + inner_product(-vec_z_1n, Gs) + inner_product(z * vec_y_n + z ^ 2 * vec_2n, H_y_minus1)
print("P = ", P)
assert P == inner_product(lx, Gs) + inner_product(rx, H_y_minus1)
print("Check 2 ✅")

内积参数：最后一步

但是等等……证明者不能只发送完整的向量 l 和 r，这会泄露太多信息。

这正是内积参数再次发挥作用的地方！

为了做好准备，我们稍微重新排列上面的等式：

$P = A + x \cdot S - \langle z \cdot 1_n, G \rangle + \langle z \cdot y^n + z^2 \cdot 2_n, H' \rangle - \mu \cdot H = \langle l, G \rangle + \langle r, H' \rangle$

然后我们将内积结果 $\hat{t}$ 放入其中：

$P + \hat{t} \cdot Q = \langle l, G \rangle + \langle r, H' \rangle + \langle l, r \rangle \cdot Q$

（其中 Q 是用于 IPA 证明的随机椭圆曲线点）。

这是 IPA 的输入：证明者生成一个简短的递归证明，证明 $\langle l, r \rangle = \hat{t}$。

如果你忘记了，可以在这里找到我们之前的文章：分解 Bulletproofs（第 1 部分） 和 展开 Bulletproofs 魔法（第 2 部分）。

Q = E.random_point()
print("Remember that tx = <lx,rx>")
ipa_proof = ipa(lx, rx, Gs, H_y_minus1, tx, Q, Fr)
P_full = P + tx * Q
verify(Gs, H_y_minus1, P_full, ipa_proof[0], ipa_proof[1], ipa_proof[2], ipa_proof[3], ipa_proof[4], Q, n, Fr)
print("IPA proof ✅")

最终证明是什么样的

完整的范围证明包括：

• A 和 S
• T1 和 T2
• $\hat{t}$ 及其 blinding factor $\tau_x$
• μ（A 和 S 的 blinding）
• IPA 证明，包括：
• 来自每个 folding 步骤的 L 和 R 向量
• 两个标量表示最终的 folded 向量 l 和 r

就是这样！ 我们刚刚从头开始构建了一个完整的范围证明！🧠

从一个简单的想法开始：证明一个隐藏值介于 0 和 $2^n$ 之间，我们将一系列强大的技巧结合在一起：

• 比特分解 将值表示为 0 和 1 的向量
• 随机挑战 (x,y,z) 将每个等式联系在一起并防止作弊
• 承诺 隐藏数据，同时保持所有关系一致
• Blinding IPA 的输入和输出，因为 IPA 协议不是零知识的
• 最后，内积参数 可以高效且紧凑地验证所有内容

所有这些结合在一起，以便验证者可以确信：“证明者的秘密值在正确的范围内”，而不会了解该值本身的任何信息。

这个基础支持机密转移、私人余额和许多其他保护隐私的系统，例如我们在本文开头概述的系统。

你可以在这里找到完整的 Sagemath 脚本：range-proof.sage

进一步阅读

• Bulletproofs 论文
• Dalek crate 文档

zkSecurity 为包括零知识证明、MPC、FHE 和共识协议在内的密码系统提供审计、研究和开发服务。

了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～