非平衡油和醋，第三部分

在第一部分中，我们研究了我们希望UOV攻击者解决的问题。在第二部分中，我们有大量的油和醋，但并没有真正讨论该方案的整个不平衡部分。因此，在本三部分系列的第三部分中，我将讨论为什么我们特别使用不平衡的油和醋，并讨论Kipnis-Shamir对原始油和醋方案的攻击。

提出此攻击的论文是用矩阵的语言编写的，但在我看来，并且展示了我作为代数几何学家的偏见，当使用这种语言时，人们无法完全理解这个问题，我将用双线性形式的语言来呈现它，这是我在过去的两个博客文章中构建的。使用双线性形式是有用的，因为它允许我们展示事物而无需选择显式基，这意味着我们不必真正区分公钥和私钥。

预备知识

本节的大部分内容是线性代数，特别是双线性形式和对偶向量空间的小课程。我将尝试纯粹用矩阵来表达攻击，所以如果这对你来说太过分了，你可能仍然可以跟着攻击，但正如前面提到的，在我看来，使用双线性形式的语言可以更深入地理解。

首先，作为一个快速回顾，正如第二部分讨论的，一个UOV公钥是一组$m$个双线性形式$(\cdot, \cdot)_i$，它们具有这样的性质：存在一个子空间$O\subset X$，使得对于所有$x, y \in O, i = 1, \dots, m$，都有$(x, y)_i = 0$。这个子空间$O$就是我们正在寻找的私钥。所讨论的攻击是一种仅使用公钥的密钥恢复攻击，所以我们不需要重复签名是如何工作的，我们将只关注如何在给定双线性形式的情况下恢复这个子空间，第二部分讨论了签名方案。

我们还需要一些额外的词汇来讨论双线性形式。正特征的双线性形式有时表现得有点奇怪，所以从头开始证明一些东西是有意义的。

首先，我们需要讨论非退化双线性形式。如果对于所有向量$x \in X, x\neq 0$，至少存在一个向量$y \in X$使得$(x, y) \neq 0$，则称双线性形式是非退化的。如果你看定义双线性形式的矩阵，这相当于说这个矩阵是满秩的。

我们关心非退化双线性形式的原因是，它们允许我们在有限维向量空间中“转置”向量，即将列向量变成行向量。如果你懂量子物理学，非退化双线性形式所做的就是将ket向量变成bra向量。如果你不懂量子物理学，不用担心，这些只是量子物理学家发明的术语，因为他们对双线性形式和对偶向量空间了解不够。

要理解对偶向量空间，你只需要知道这里线性形式，即输出单个标量的线性函数，它们本身也形成一个在同一域上的向量空间，因为你可以添加线性形式并将它们与标量相乘。从概念上讲，这些实际上只是行向量，正如上面提到的，因为这些可以与列向量相乘，以给出基础域的元素，即行向量定义了所有存在的线性形式（对于有限维向量空间。无限维向量空间非常非常不同，并且稍微收回我对量子物理学家的评论，这些是量子物理学处理的，但是，理解对偶向量空间会使他们的领域更容易接近）。我们用$X^*$表示这个对偶向量空间。

为了将这一点与我们的双线性形式联系起来，双线性形式允许你做的重要事情是“柯里化”，或部分求值，也就是说，给定一个双线性形式$(\cdot,\cdot)$ 和一个元素$x \in X$，我们可以看线性形式$(x, \cdot)$。

对于非退化形式，这样做部分求值会给你一个额外的属性，即如果$\sum_{i=1}^n \alpha_i (bi, \cdot) = 0$，我们知道$\sum{i=1}^n \alpha_i bi = 0$，因为线性形式0被定义为向量空间中所有向量的0，并且第一个参数中的线性意味着$\sum{i=1}^n \alpha_i (bi, \cdot) = \left(\sum{i=1}^n \alpha_i bi, \cdot\right)$，所以根据非退化的定义，可以得出$\sum{i=1}^n \alpha_i b_i = 0$。这意味着，如果$(b_1, \dots, b_n)$是线性独立的，那么$(b_1, \cdot), \dots, (b_n, \cdot)$也是线性独立的。这证明了我上面所说的有限维向量空间与其对偶空间具有相同维度的说法，并且意味着每个非退化双线性形式都为我们提供了一种将列向量映射到行向量的方法。仅仅为了将纸张旋转90度似乎需要做很多工作，但正如我所说，量子物理学家仍然为认为他们可以自己更好地旋转纸张付出了代价。

接下来，我们需要讨论正交性。这个术语只有在特征0中才有几何意义，但我们仍然可以代数地使用它：如果$(x, y) = 0$，则两个向量$x, y \in X$被称为正交。对于一个子向量空间$V \subset X$，我们定义$V^\perp := {x \in X\;;\;(v, x) = 0\, \forall v \in V}$。通过这个定义，我们可以将我们的双线性形式的陷门重新表述为存在一个子空间$O \subset X$，使得$O \subset O^{\perp_i}$。基本上，一个子空间在公钥的所有双线性形式中与自身垂直。

虽然这在几何上显然是无意义的，但我们可以至少将正交性的一个属性恢复到正特征中，那就是正交空间的维度：

对于一个非退化双线性形式$(\cdot, \cdot)$，和一个子向量空间$V\subset X$，我们有$\text{dim}\, V^\perp = \text{dim}\, X - \text{dim}\,V$。要看到这一点，取$V$的一个基。对于每个基向量$b_i$，我们再次看线性形式$(b_i, \cdot)$。这给了我们$\text{dim}\,V$个线性独立的线性形式，所有这些形式都在$V^\perp$上消失。我们可以将这些形式视为一个线性函数$X \to K^{\text{dim}\,V}$，并且由于它们是线性独立的，我们知道这个线性函数是满秩的。在所有形式上消失使得$V^\perp$ 成为该函数的核，并且根据核秩定理，这意味着 $\text{dim}\, V^\perp = \text{dim}\, X - \text{dim}\,V$。

攻击

在完成了所有这些之后，我们现在可以看看攻击本身。所以在下面，我们有$m$个双线性形式$(\cdot, \cdot)_i$，定义在一个$n$维向量空间$X$上，$n = 2m$，即油向量和醋向量一样多，一切都是“平衡的”。我们还有一个秘密的，$m$维子向量空间$O\subset X$使得对于所有$i = 1, \dots, m$，$O\subset O^{\perp_i}$，如上所述。这里需要注意的一件事是$\text{dim}\, O^{\perp_i} = n - m = m = \text{dim}\, O$，所以在这种平衡情况下，并且仅在这种平衡情况下，我们进一步得到$O = O^{\perp_i}$，因为具有与空间相同维度的子向量空间等于该空间。

Kipnis-Shamir攻击背后的主要思想是，双线性形式很难，但线性函数很容易，并且对于两个非退化双线性形式$(\cdot, \cdot)_1$和$(\cdot, \cdot)2$，恰好存在一个线性函数$\varphi{12}$，使得对于所有$x, y \in X$，都有$(x, y)_1 = (\varphi(x), y)_2$。我们知道这一点，因为$(\cdot, \cdot)_1$和$(\cdot, \cdot)_2$都是非退化的，所以两者都可以将$X$的基映射到对偶向量空间$X^*$的基，所以$\varphi$是由这个基改变给出的映射。更具体地说，如果$(\cdot, \cdot)_i$由矩阵$A_i$表示，即$(x, y)_i = x^T A_i y$，那么$\varphi$，作为一个线性函数，由$(A_1A_2^{-1})^T$表示，因为$(\varphi(x), y) = ((A_1A_2^{-1})^Tx)^TA_2y = x^T A_1 A_2^{-1}A_2y = x^T A_1y$。如果我们没有完成所有关于双线性形式的工作，我们现在需要添加两行证明，证明这在基改变下是不变的。我选择了写几段价值的线性代数，我们当然都会同意，这是更可取的。

到目前为止，没有什么特别的。你有一堆双线性形式，你可以定义这个线性函数。但现在，我们可以问$\varphi(O)$是什么。我们知道对于任何向量$x \in O$，对于所有向量$y \in O$，$(x, y)_1 = 0$，所以我们也知道$(\varphi(x), y)_2 = (x, y)_1 = 0$，所以我们知道$\varphi(x) \in O^{\perp_2}$。但如上所述，在平衡情况下$O = O^{\perp_2}$，所以$\varphi(x) \in O$。这意味着$\varphi(O) = O$（从技术上讲，我还没有证明等式，但这很容易通过再次应用非退化来得出）。这意味着$\varphi|_O$，$\varphi$限制到子向量空间$O$是一个自同态。

但对于一个线性函数，限制到一个作为自同态的子向量空间与说这个子向量空间是特征空间的乘积是一样的。我们可以计算线性函数的特征空间。就其本身而言，这只有适度的帮助，因为我们不知道$\varphi$的哪些特征空间是$O$的一部分，哪些不是。但我们不只有一个$\varphi$，对于每对双线性形式，我们都有一个线性函数。我们可以相交特征空间，并找到多个线性函数的公共特征空间。两个随机线性函数不太可能共享一个特征空间，我们有$m(m-1)/2$个线性函数共享一个特征空间。所以那个公共特征空间就是$O$。我在下面描述了如何计算那个共享特征空间，但更多细节请参见论文。

总而言之，攻击算法的工作原理如下：

1. 丢弃所有奇异矩阵，因为它们对应于退化双线性形式。
2. 计算足够多的$i, j$的$A_i A_j^{-1}$。
3. 取计算出的矩阵的任意线性组合$C = \sum{i, j = 1}^m \alpha{ij}A_i A_j^{-1}$
4. 计算$C$的特征多项式并将其因式分解。
5. 由于公共特征空间，特征多项式将始终具有$m$次的因子。但它可能有更多的因子。如果还有更多的因子，丢弃并尝试新的线性组合。如果你没有找到这样的矩阵和因式分解，继续执行步骤7。
6. 根据Cayley-Hamilton定理，在矩阵上求值的特征多项式的因子的核是矩阵的特征空间。由于我们的矩阵具有仅有两个因子的特征多项式，因此两个特征空间之一是油空间，我们可以快速验证。
7. 阅读论文，了解为什么找到这样的特征多项式非常有可能，所以你永远不会到达这一步。

几何解释

我必须承认，当我第一次读到这个攻击时，我发现它非常具有破坏性。对一个方案家族的一个成员进行多项式时间攻击是一件非常可怕的事情，虽然这个攻击显然需要$n = 2m$才能工作（否则整个特征空间论证就会崩溃），但至少我想看到某种形式的论证，为什么$n > 2m$不仅仅是在缓解这个特定的攻击，而且从根本上来说，它具有某种比平衡情况更复杂的结构。

我想我已经找到了这样一个论证，但作为一个公平的警告，接下来将是一些不留情面的，深入的，代数几何的深水区。好吧，深水区的浅水区，但你明白了我的意思。我将尽力使论证更容易被更广泛的受众理解，但你必须接受我所说的一堆东西的表面价值。整个论证是我对UOV进行的更深入调查的一部分，但这应该是一篇不同的博文，或者可能是一篇CFAIL论文或其他类似的东西。

免责声明已经给出，我们开始：

如果一个代数几何学家被赋予$m$个多项式，即使它们只是二次形式，我们的基本本能就会发挥作用，我们研究通过将所有这些多项式设置为零而获得的几何对象。我将此称为油醋簇，即$S = \text{Spec} K[X]/((X, X)_i)$。请注意，即使这些多项式是齐次的，我们也需要控制住我们动物般的几何冲动，现在不要看$\text{Proj}$。这个簇是$\mathbb{A}^n$的一个子簇，并且由于它由$m$个多项式给出，假设这些多项式是完全交集，它将是$n - m$维的。对于非几何学家：这类似于具有$m$个线性方程如何创建一个$n – m$维向量空间，“完全交集”等同于事物是线性独立的，只是事物可能以更有趣的方式出错，一般来说，事物弯曲得更多，但重要的是，如果你取随机多项式，它们很可能是完全交集，所以如果我们的油醋多项式不是，那本身就是非凡的。不幸的是，如果不计算Gröbner基，就无法真正检查多项式是否是完全交集，参见第一部分，但当我尝试我可以用Gröbner基计算的微小案例时，直到$n = 2m$，事物都是完全交集（对于$n < 2m$，如我们所见，它不可能是完全交集）。但我没有计算完全交集在一般情况下有多可能。

另一件需要注意的事情是，$O$，被视为$\mathbb{A}^n$的线性子簇，是$S$的一个子簇，因为根据定义，二次形式在$O$上求值为0。并且$O$是$m$维的。这表明对于$n < 2m$，$S$不能由完全交集中的多项式定义，因为它的维度$m$大于$n – m$。

所以在平衡情况下，其中$n = 2m$，$S$是$m$维代数簇，具有$m$维线性子簇。换句话说，$S$的一个不可约分量。Kipnis-Shamir攻击将这个线性分量从$S$的其他非线性分量中分离出来。

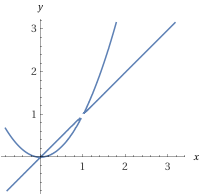
对于$m = 1$，$n = 2$的OV簇的艺术家印象。你可以看到线性子空间作为不可约分量。请注意，这是一个3次多项式，所以它实际上不是一个有效的OV簇，否则它看起来会很无聊。

然而，在不平衡情况下，$n > 2m$，所以$\text{dim}\,S = n - m > m = \text{dim}\,O$。这使得$O$成为一个余维度大于0的闭子簇，即$O$位于$S$的某个自身非线性的，不可约分量上。至少在概念上，对我来说，有意义的是，可能存在一种算法可以提取线性不可约分量，但非线性分量的线性闭子簇更难以分离。

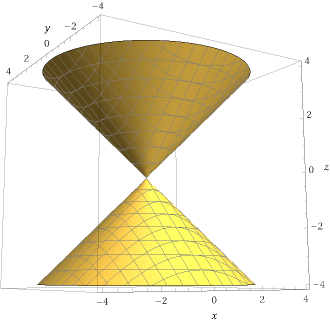
一个$m = 1$，$n = 3$ OV簇的图。有很多线性子空间可供选择（通常情况并非如此），但它们都位于一个决定性地非线性的不可约分量上。这仍然不是最好的图片，因为绘图软件将我限制在仅三个维度上。

• 标签 密码学

• 原文链接： keymaterial.net/2025/01/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～