FRI为什么有效？

FRI 协议是当今许多生产环境中部署的 SNARKs 的关键组成部分。 已经有很多很棒的讲座解释了 FRI 是什么以及它是如何工作的。 其中，我强烈推荐 Dan Boneh 的 ZK Whiteboard Session 模块（S2M7, S2M8）。 对于那些喜欢更实用的介绍的人，我建议学习带有配套代码的教程，例如 StarkWare 的 STARK 101 的第三部分。

在这篇文章中，我不会重复上面列出的精彩教程的内容。 我想回答的问题是：为什么 FRI 是安全的？ 为什么 执行此协议可以让我们满意地保证证明者的初始消息接近 Reed-Solomon 码字？

这些问题通常由协议的安全证明来回答。 不用说，FRI 的安全证明不是入门级的读物。 然而，与合著者 Albert 和 Benedikt 一起，我最近尝试给出一个更简单的证明（可在 ePrint 上找到）。 这篇文章是我们在此使用的想法的总结。

我假设读者熟悉 FRI 及其相关的工具和术语。 我将首先快速回顾协议的机制，主要是为了定义我将使用的符号。 然后我将介绍“证明者消息图”，这是 FRI 安全证明的有用工具。 之后，我们将讨论 FRI 中使用的“折叠”操作的关键安全属性，并最终论证该协议是安全的。

FRI 回顾和符号

FRI 协议用于证明证明者函数 f0 接近给定的 Reed-Solomon (RS) 码。 它的工作原理是使用验证者的挑战来连续“折叠”证明者的函数。 最终，当函数足够小时，验证者可以完整地读取它，并检查它是否是来自较小 RS 码的码字。 然后，验证者在所有证明者的消息之间执行抽查，以确保折叠操作的计算正确。

在本文中，我将使用符号 RS[F,L,d] 来表示在有限域 F 上定义的 Reed-Solomon 码，其评估域为 L⊆F∗，且度数界限为 d∈N。 RS 码的速率写为 ρ=d/|L|。

具体来说，我将考虑初始域 L0 是单位根的 16 次方，初始度数界限是 d0=8 的示例。 连续代码在单位根的 8 次方、4 次方和 2 次方上定义，其度数界限分别为 4、2 和 1。 我将写 f0、f1、f2、f3 来表示证明者的消息，α1、α2、α3 来表示验证者的折叠挑战。

跟踪证明者的消息

在我们的安全分析中，我们需要注意的第一件事是，证明者可能发送了一个不是 Fold(fi,αi+1) 的函数 fi+1（即，使用挑战 αi+1 对 fi 的诚实折叠）。 为此，我们定义了证明者消息图。 图的每一层代表一个评估域和该域上的证明者消息。 当点相关时，我们可以在层之间绘制边：例如，第 0 层中的点 s 和 −s 都有一条边指向Layer1中的点 s2。 该图如下所示。

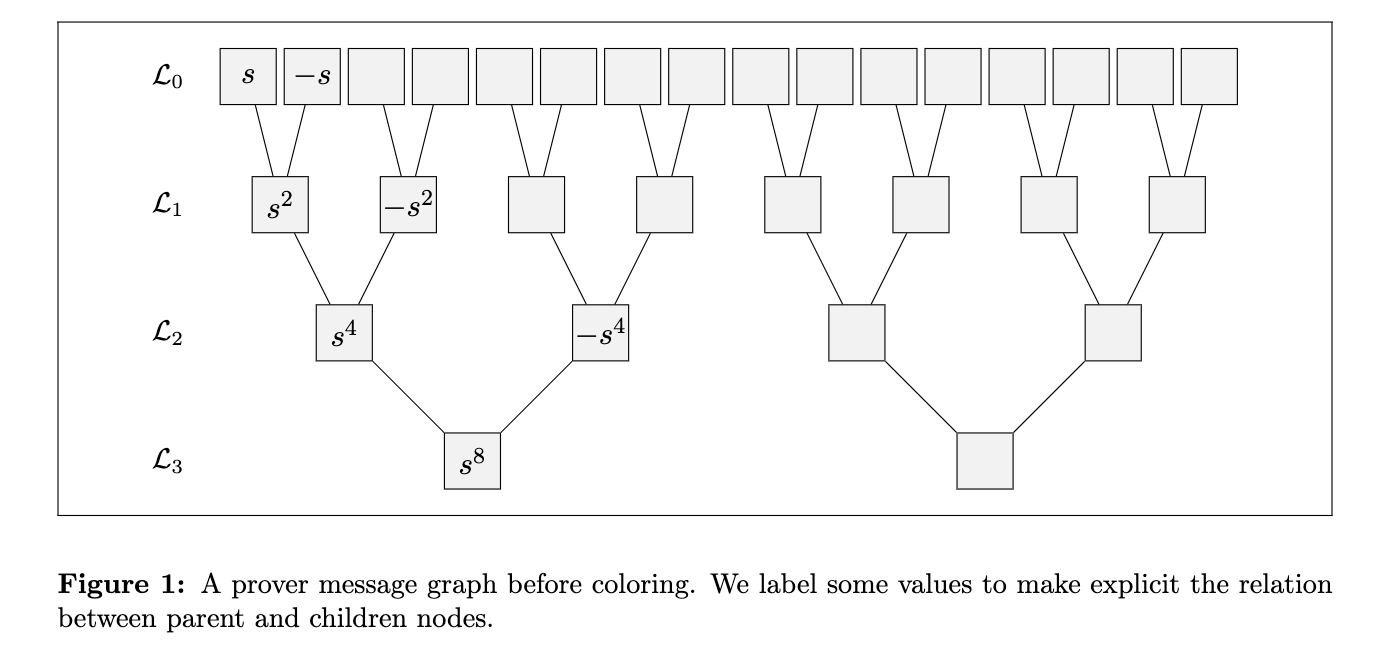
我们现在可以为图形着色，以指示当验证者运行查询阶段时会发生什么。 我们将使用绿色表示接受查询，红色表示拒绝查询。 为了执行着色，我们将节点分成 3 个一组：第 i 层中的一个节点及其在第 i−1 层中的两个相关节点。 如果 Fold 操作在这些节点上计算正确，我们保持它们不变；否则，如果 Fold 不正确，我们将第 i 层上的节点标记为 X。 具体来说，使用上图中的标签，我们将考虑组 (s,−s,s2)，从 f0(s) 和 f0(−s) 计算 Fold(f0,α1)(s2)，如果该值与 f1(s2) 不一致，则将节点 s2 标记为 X。 这正是验证者通过其检查所做的事情！

一旦我们考虑了所有三元组，我们就可以分配颜色。 所有从第 0 层的叶子开始并以 X 结尾的路径都被标记为红色（不包括 X）。 我们这样做是为了反映这样一个事实，即从这样的叶子开始，验证者将不可避免地到达 X 并注意到不一致。 所有其他节点都着色为绿色。 下面给出一个例子。

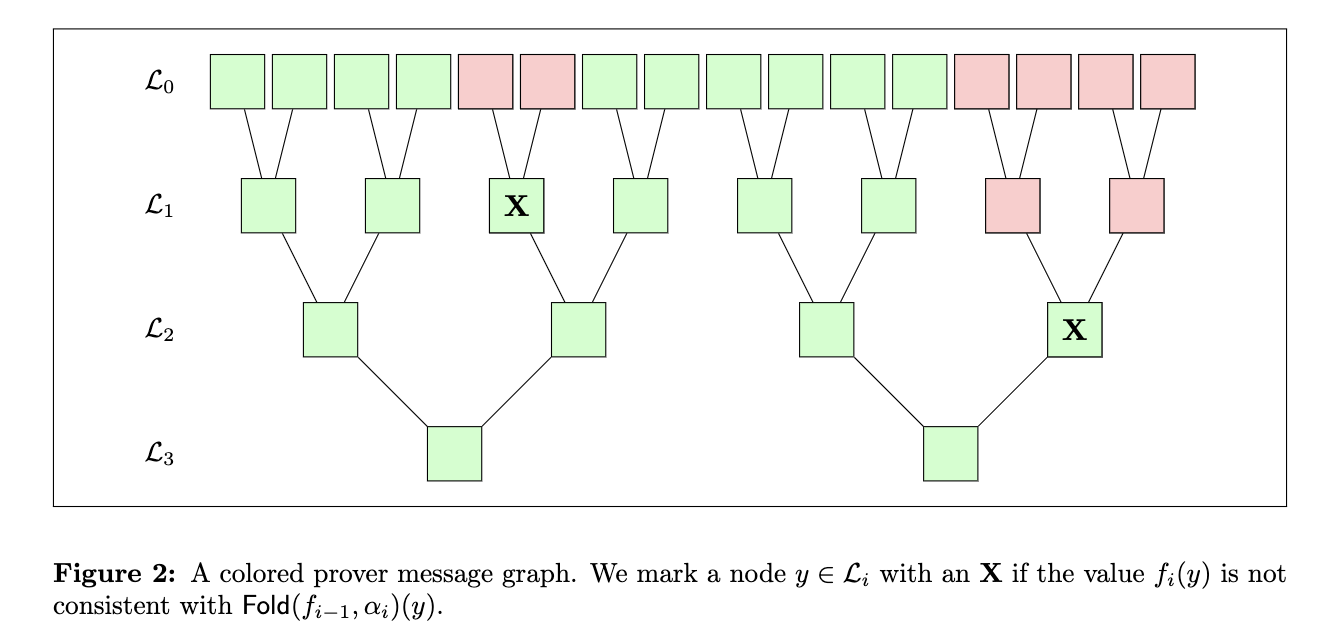
在这一点上，我想强调一些关于着色图的重要直觉：

1. 如果验证者在红色节点处查询第 0 层，它将拒绝。因此，绿色节点的比例恰好是验证者接受的概率。

2. 红色从 X 向上传播。这意味着证明者不会通过不诚实地折叠来获得优势。此外，我们看到它这样做的越晚（例如，在最后一轮），它就越会降低被接受的概率。

3. 绿色节点集表示所有折叠都诚实执行的集合。

现在，关键问题仍然存在：当第 0 层中存在很大比例的绿色节点时，为什么我们可以推断出 f0 接近 RS[F,L0,d0]？正如我们接下来将看到的，这是因为验证者检查最终函数是否在最终代码中，并且来自 Fold 的一个重要的安全属性。

Fold 的关键属性

在 FRI 交互结束时，验证者完整地读取最终函数，并检查它是否在最终代码中。 在我们的示例中，验证者读取 f3:L3→F 并检查它是否是一个常数多项式。 理想情况下，这个观察结果可以在证明者消息图中“冒泡”上升。 我们可以将理想属性表述如下：

• (理想属性) 如果存在一个码字 ui∈RS[F,Li,di] 与 fi 在绿色节点上一致，那么存在一个码字 ui−1∈RS[F,Li−1,di−1] 与 fi−1 在绿色节点上一致。

如果具有这样的属性，我们的任务就解决了！ 我们将通过图形向上归纳应用该属性，并发现第 0 层中绿色节点的比例至少是 f0 和码字之间的一致性。 不幸的是，事情并非如此简单。 理想属性并非总是成立。

另一方面，我们可以做的是放宽此属性，并且仅要求它_以高概率_在验证者的折叠挑战中成立。 这将产生以下真实属性：

• (真实属性) 如果 (a) 存在很大一部分绿色节点，并且 (b) 存在一个码字 ui∈RS[F,Li,di] 与 fi 在绿色节点上一致，那么以高概率超过验证者消息 αi，存在一个码字 ui−1∈RS[F,Li−1,di−1] 与 fi−1 在绿色节点上一致。

“很大一部分”绿色节点的概念是有意宽松的。 让我们将 B⋆ 表示为“足够大”的度量。 理想情况下，我们希望 B⋆ 尽可能低，正如我们稍后将在我们的论证中看到的那样（参见最终论证，情况 1）。 目前，我们对 B⋆=1+ρ2 的情况有令人满意的结果。 有私人草案在流传，证明了 B⋆=ρ 的属性，我们甚至推测这个比例可以小到 B⋆=ρ（回想一下 ρ<1，因此 ρ<ρ）。 为小边界证明此属性是一个开放问题，以太坊基金会正在为此设立高达一百万美元（！！）的奖金。

最终论证

现在，我们可以使用“真实属性”完成我们的安全分析，该属性允许通过证明者消息图中足够大的绿色节点集来冒泡一致性 。 唯一的微妙之处是，我们需要处理在图的任何层中绿色节点少于 B⋆ 比例的情况。 我们通过分离两种情况进行论证：

1. 情况 1，存在一层 i，其绿色节点的比例小于 B⋆。

2. 情况 2，所有层至少具有 B⋆ 比例的绿色节点。

情况 1：少量诚实折叠

我们首先考虑至少有一层无法应用真实属性的情况。 也就是说，第 i 层具有小于 B⋆ 比例的绿色节点。 等效地，该层必须至少具有 (1−B⋆) 比例的红色节点。 下图显示了“情况 1”的示例。

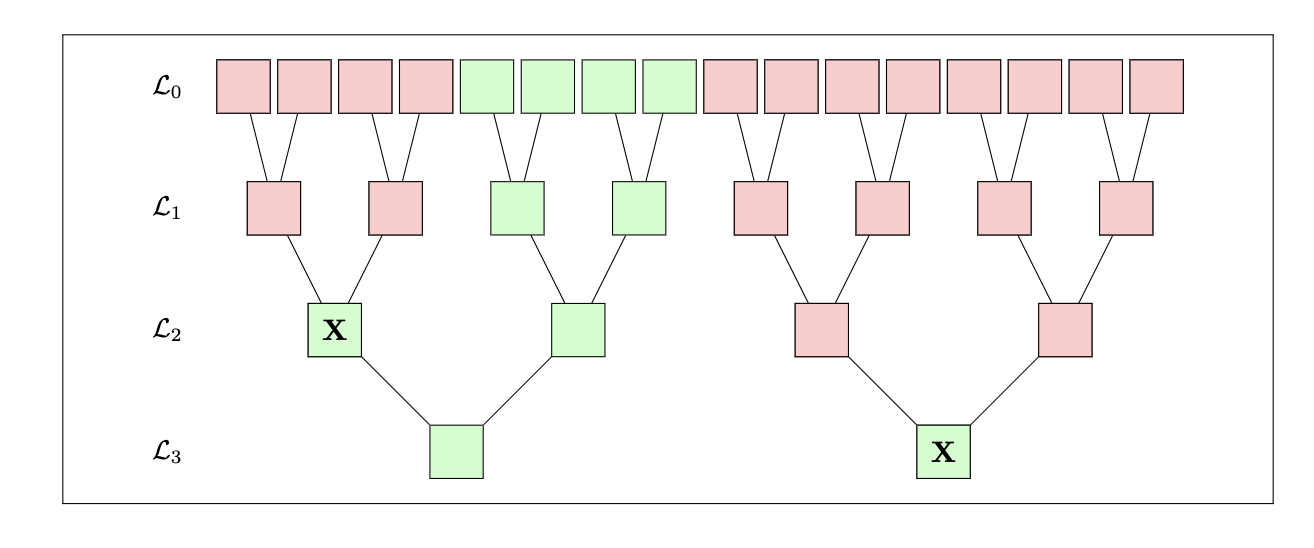
回想一下，根据我们的图形着色规则，所有通向 X 的路径都标记为红色。 从该规则可以很容易地确定“红色总是向上传播”。 因此，我们可以证明，如果存在至少具有 (1−B⋆) 比例的红色节点的层，则其上方的所有层也将至少具有 (1−B⋆) 比例的红色节点。 特别是，第 0 层至少具有 (1−B⋆) 比例的红色节点。

从这个讨论中，我们得出结论，第 0 层最多具有 B⋆ 比例的绿色节点，并且验证者将以 B⋆ 的概率接受。 在实践中，我们希望拒绝行为类似于情况 1 的证明者，因此希望 B⋆ 尽可能小。

情况 2：大量诚实折叠

对于情况 2，我们可以参考图 2 中给出的说明。 由于绿色节点集足够大，我们可以应用我们的“真实属性”，并得出结论，一致性会冒泡上升假设所有折叠挑战都是“好的”。 因此，以仅具有“好的”挑战为条件，f0 和初始代码 RS[F,L0,d0] 之间的一致性至少是顶层中绿色节点的比例。 或者，在距离（而不是一致性）方面，我们已经表明，验证者的接受概率最多为 1−δ，其中 δ=Δ(f0,RS[F,L0,d0]) 是 f0 和初始代码之间的相对距离。

结论

这结束了我们对 FRI 工作原理的概述！ 该论证源于 Fold 函数的一个重要属性：当存在足够大比例的诚实折叠时，“一致性会冒泡图”。 我们通过论证必须存在大量不诚实的折叠来处理诚实折叠的比例不够大的情况。 在这种情况下，验证者可能会查询它们并拒绝。

目前正在进行研究，以证明该属性对于尽可能小的“大”概念都成立。 这使我们可以尽可能多地停留在情况 1 中，并为我们提供了更严格的安全界限。 反过来，更严格的界限使我们可以获得更短的证明，并在相同的安全级别下减少证明者和验证者的工作。

致谢

感谢 Varun Thakore、0xteddav (David)、Albert Garreta 和 Kobi Gurkan 仔细校对本文并分享许多有用的问题、更正和建议。

zkSecurity 为包括零知识证明、MPC、FHE 和共识协议在内的密码系统提供审计、研究和开发服务。

了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～