ZK编年史：计算模型

为了获得更具互动性的体验，请在我的个人博客 Arkana 上阅读本文。

嘿！很高兴你从上一篇文章中幸存下来！

哦，耶耶，没事没事！

不用逞强，我知道这可能有很多东西。为此感到抱歉。

我们上次相遇最重要的结论也许是，我们可以证明高效验证通用计算是可能的。但是，我们也提到我们很少将程序编写为算术电路。我的意思是……萝卜青菜各有所爱，但是你得是哪种疯子才会把程序写成连接的加法和乘法门？

相反，我们通常使用更高级别的抽象，以 编程语言 的形式。我们使用循环、条件语句、函数。我们该怎么办？

我的 Python 程序怎么办，兄弟？

玩笑归玩笑，这里真正的关键问题是：为什么是电路？ 即使我们已经为它们提出了一些好的观点，比如它们的可分解性，但很难摆脱我们想要证明其他类型程序的一些属性的想法。

所以今天，我想引导你了解这些不同计算模型之间的联系。这些将揭示可验证计算的一些核心方面，并开启一个充满可能性的世界。

我不知道你怎么想，但这听起来令人兴奋！让我们立即深入研究！

计算

我们今天的旅程从一个简单的问题开始：执行计算意味着什么？

乍一看，这似乎是一个愚蠢的问题。你编写代码，计算机执行它，你得到结果。这有什么复杂的？

但是，如果我们更仔细地考虑它，事情就会变得有趣起来。例如，用 JavaScript 编写一个程序来添加两个数字与编写 汇编指令 来添加两个数字是不同的。编写一个电路来添加两个数字也不同。

这些都是相同的计算吗？它们肯定看起来不同，使用不同的语法、不同的操作，也许最明显的是，不同的抽象级别。我们从电路门的简单性，到 CPU 的复杂架构，再到 JavaScript 的所有解释性花招。

然而，直观地看，这些例子都做了同样的事情：它们添加了两个数字！

这个问题是计算理论的核心：对于不同的过程计算相同的事情意味着什么？ 更重要的是：一些计算模型从根本上来说是否比其他模型更好或更强大，或者它们在某种意义上都是等价的？

毫不奇怪，有一个完整的数学（和计算机科学）分支致力于研究这些关于计算模型的问题。

计算复杂性理论

简而言之，计算复杂性理论 是研究什么可以被 高效计算 以及什么不能被 高效计算 的学科。

其核心概念之一是 复杂性类：具有 等价难度 的问题组，我们可以尝试为它们找到高效的算法。

因此，我们可以研究 计算模型 来解决这些类中的问题，而不是迎合任何特定问题。

这些计算模型实际上是 数学抽象，它们捕捉了“计算某物”的本质，而与编程语言或硬件无关。

以下是复杂性理论研究的一些主要模型。其中一些肯定会让你想起：

• 图灵机：基本上是计算模型的 老祖宗。 想象一条包含 单元 的无限长的纸带，其中包含符号。机器在任何时候都指向纸带中的单个位置，并且可以向左或向右移动。根据符号的值，并基于一组简单的规则，纸带的这个 指针 可以向左或向右移动到其他位置，甚至可以在纸带上书写。
• 随机存取机（Random Access Machine, RAM）：一种更接近真实计算机的模型，具有可以直接访问的内存地址。这本质上就是你的笔记本电脑在底层的工作方式。
• Lambda 演算：一种纯粹的数学方法，其中 一切都是函数。只有三个操作：定义函数、将函数应用于参数以及替换变量。没有循环，没有 if 语句，没有改变变量 —— 只有纯粹的函数组合！
• 布尔电路：我们已经对这种模型烂熟于心了。就像把计算表示成一堆逻辑门。我们在第一篇文章中提到数独时就见过！

有了这些，我们现在可以深入探讨 Cook-Levin 定理。我们不会证明它，因为那需要不止一篇文章！而且，仅仅是陈述本身就能给我们带来很多信息。如下：

NP 中的任何问题都可以在多项式时间内归约到电路可满足性问题

是的！还记得我们的 电路可满足性 (CSAT) 问题吗？事实证明，它不仅是一个 NP 问题，而且它还与所有其他 NP 问题 等价 （直到一个多项式时间因子）。

我构建关于电路可满足性和电路评估之间讨论的方式，最终描绘了一幅非常不同的图景，关于电路可满足性的重要性和普遍性……正如我们现在所知，这与事实相去甚远！

所以最后，电路可满足性具有核心的理论作用。由于 Cook-Levin 定理，我们可以采用 任何 NP 问题，并将其转换为 CSAT 实例。该定理保证这是可能的，但机制可能会有所不同。

一旦我们有了 CSAT 实例，我们就可以生成一个算术电路。这使我们可以得出结论：

算术电路是 有界 计算的通用模型

是的！我们关心的任何计算都可以表示为算术电路。这是到目前为止我们一直在研究电路的主要原因，除了它们拥有的有趣特征：它们在数学上是 简单的、可分解的、可能是 结构化的，而且现在最重要的是，它们是 通用的。

不错

这还有一个很好的结果：我们可以使用 CSAT 作为 支点 来证明 任何 两个 NP 问题是等价的。

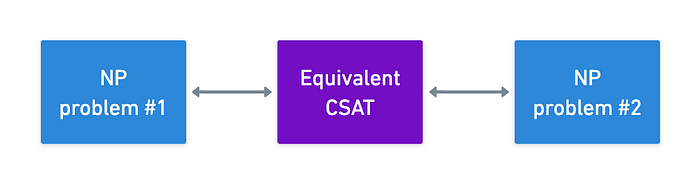
真正酷的是，我们可能会为一个特定的 NP 问题找到一个非常有效的证明系统，并且我们至少在理论上可以将任何其他 NP 问题转换为该形式 —— 当然，也需要付出相关的转换成本（我们通常称之为膨胀因子）。

这暗示了一个强大的微妙之处：通过适当的转换，我们可以将任何证明算法应用于任何问题！

至于这是否是一个好的策略……那是另一回事了！

语言和判定性问题

好的！我们已经成功地确定了电路是通用的。

虽然这具有巨大的理论价值，但我们需要进行一个微妙的视角转变 —— 随着我们深入到 ZK 系统中，这个转变将变得至关重要。

ZK 概览

为了激发这一点，让我们简要地进一步讨论一下第一篇文章中关于零知识的讨论。

现在正式定义我们所理解的零知识还为时过早。然而，这并不意味着我们不能通过稍微更复杂的概念来开始接近实际的定义。

我们当时不知道的一件事是，我们可以使用电路来表示计算。现在我们知道了，我们可以粗略地定义 ZK 的含义。它是这样的：证明者 将尝试说服 验证者 他们知道给定电路的某个输入 $w$，以便电路的 输出 是给定的值：

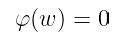
预期的输出值通常是 0。通过添加一个减去 预期输出 的额外门，任何电路都可以轻松转换为这种格式。

使这成为零知识的原因是，验证者可以在 不了解 w 的情况下被说服。

够简单吧？

请注意，在上面的公式中，验证者实际上并不关心 $w$ 的实际值，只是关心是否存在这样的 $w$，并且这个问题只有两个有效的答案：是 和 否。

以这种方式陈述的问题称为 判定性问题，它们与我们可能实际上关心寻找问题的 有效解决方案 的问题类型直接相反。

例如，我们希望找到一个满足电路的输入！

这种类型的问题称为 搜索问题，我想对于大多数人来说，它们可能感觉更自然。我们有一个问题，我们找到一个有效的解决方案，搞定。谁关心所有可能的解决方案？

嗯，ZK 关心：验证者只需要知道存在有效的解决方案，而无需了解其值！

此外，这两种类型的问题密切相关：如果你可以解决搜索问题，你显然可以解决判定性问题（因为你已经找到了一个解决方案！）。

另一方面有点棘手，但总的来说，如果你可以有效地解决判定性问题，你通常也可以有效地解决搜索问题。这是通过一种称为 自归约性 的技术完成的。

为此，计算复杂性理论使用一个非常严格的数学框架（称为 语言）来研究判定性问题。

语言

在你问之前：不，这与 Python 或 Rust 等编程语言无关。

语言 只是一个字符串集合，用于编码问题的 是 实例。

什么？

我认为通过一个例子更容易理解这一点。让我们考虑以下问题：当给定一个数字时，我们问“它是素数吗？”

当然，你可以继续编写一个算法来确定这一点。但 从概念上讲，我们可以做一些其他的事情。让我们将集合 𝓛ₚ 定义为：

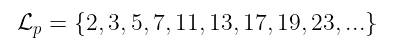
或者更简洁地说：

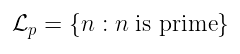
现在我们所说的内容应该非常清楚了：这正是 所有字符串（在本例中为数字）的 集合，对于这些字符串，我们最初问题的答案是 是。 并且检查一个数字是否为素数，前提是我们事先知道这种语言，就像检查该数字是否属于 𝓛ₚ 一样简单。

我知道你在想什么：有什么意义？

在我们的示例中，找到 𝓛ₚ（当然是一个无限集）如何比确定单个数字是否为素数更容易？

是的，这可能看起来像是一种毫无意义的形式主义，但语言实际上 非常强大。 通过以这些术语构建问题，我们可以：

• 精确地讨论 解决 问题意味着什么（找到属于 𝓛 的值）。
• 将复杂性类定义为 语言集。
• 推理问题之间的 归约。

例如，我们的 通用 电路可满足性问题可以被描述为一种语言：

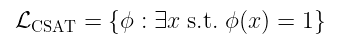
这是 所有电路 的集合，这些电路 至少有一个满足它的输入。然后，判定性问题会询问一个特定的电路 $\phi(X)$ 是否可满足，这等同于询问它是否属于该语言！

或者，我们可以为特定的电路定义另一种语言，作为其所有满足输入的集合。在这种情况下，#SAT（计数问题）的解决方案只是返回所述语言的大小！

证人

现在，这是 ZK 变得有趣的地方。

我们提到 NP 问题是那些我们可以快速验证解决方案的问题。 既然我们已经进入了正式的理论，也许现在是更准确地定义我们所说的 验证 的好时机。

在语言框架中，验证涉及 三个部分：

• 问题实例 ($x$)，它表示我们试图解决的问题 (例如，一个特定的数独谜题，一个给定的电路)。
• 证人 ($w$)，它只是一条证据，证明 $x$ 有一个解决方案。
• 验证者 (𝓥)，它是一种算法，用于检查 $w$ 是否是 $x$ 的有效证据。

有了这些部分，我们可以提出以下内容：如果存在 多项式时间验证者 𝓥 和 多项式大小的证人 $w$，则语言 𝓛 在 NP 中，使得：

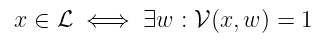
是的……这到底是什么？

用火烧死它！！

冷静，我罩着你。用简单的英语来说，这就是说，对于 NP 问题，验证者 𝓥 可以通过使用证人 $w$ 在多项式时间内（因此，快速地）验证 $x$ 的解决方案。

但是这个 $w$ 可能是什么？到目前为止，我们的两个例子揭示了：

• 在数独中，$x$ 是一个部分填充的网格，$w$ 是谜题的完整解决方案，而 𝓥 只是检查所有行、列和正方形是否包含从 $1$ 到 $9$ 的所有数字。
• 在 CSAT 中，$x$ 是我们正在处理的电路，$w$ 是一个满足电路的输入（因此，输出 $1$ 或 TRUE），而 𝓥 的工作方式是用输入 $w$ 评估电路，并检查获得的输出。

在这两种情况下，验证显然都很快。不过，证人可能会引起一些关注：它们是 问题的有效解决方案！

等等……有效的解决方案？这意味着验证者将了解问题的解决方案！这难道不会破坏我们对零知识的定义吗？

与其进入恐慌模式，我想我们最好为了心理健康而问自己这个根本性的问题：证明者是否有可能保持 $w$ 的私密性，但仍然以某种方式说服验证者 $x \in 𝓛$？

就像：“我知道这个电路的一个输入 (w) 使得输出为 TRUE，但我不会告诉你它是什么……但我仍然可以说服你！”。

当然，这绝对是可能的（否则我们就不会在这里了！）。

关键在于我们可以尝试证明 $w$ 存在，而不泄露它。而 这 是定义零知识的典型方面。

此外，证人并不总是必须是完整的解决方案。它只需要是充分的证据。高级 ZK 系统使用压缩的或巧妙结构的证人，这有助于提高证明的效率。

唉，所有这些说起来容易做起来难。我们将在适当的时候开始研究实现这一目标的方法，但至少这个新的语言框架为我们提供了一种更清晰的方式来表述我们的目标：

证明 x 属于该语言，同时隐藏证人 w

换句话说：证明电路是可满足的，而不泄露实际的满足输入！

从理论到实践

好的，我们已经介绍了很多理论。 电路是通用的，语言为我们提供了一个正式的框架，证人有助于 ZK，是的，是的……但这实际上如何帮助我证明事情？ 这在 实践中是如何运作 的？

这是一个绝妙的问题……

嗯，在所有这些理论轰炸之后，这里有一个好消息：你不用手动编写算术电路。

简直是疯了！

我们之前看到的 Cook-Levin 定理允许我们做一些很好的事情：我们可以构建 编译管道，将任何计算转换为可证明的形式。

为此，现代 ZK 系统使用 前端-后端架构。

简而言之，你要做的是以更自然的方式编写你的计算，使用以下方法之一：

• 领域特定语言 (DSL)，如 Circom 或 Noir，我们在其中编写类似于电路的代码，但仍然比该死的门更具可读性。
• 通用语言，如 Rust 或 Python。

前端处理这些表示形式，并将它们转换为合适的格式，这些格式只是 电路的代数表示形式，例如 R1CS、PLONK 算术化 和 AIR。

别担心，我们稍后会介绍这些内容！

然后，后端采用这些电路表示形式并使用证明系统（如 GKR，或其他我们稍后将探讨的系统）来生成实际的 ZK 证明。

当然，如果没有我们今天介绍的理论结果，整个管道是不可能实现的！

Cook-Levin 保证 任何计算 都可以归约到 CSAT 问题，这给了我们极大的通用性。当然，这些转换是有成本的，不同的证明系统会做出不同的权衡，甚至可能是为特定情况量身定制的 —— 所以我们必须谨慎选择。

但是，嘿，至少我们有一些回旋余地！

总结

今天的理论就讲到这里！

我们最初的简单问题引导我们走上了计算复杂性理论中一条紧张的理论道路 —— 研究不同的计算模型及其关系。

这揭示了一些重要的事情：模型在根本上是等价的，并且问题可以在同一复杂性类中的一个内部进行转换（直到多项式膨胀）。 特别是，Cook-Levin 定理展示了如何将任何 NP 问题归约到电路可满足性问题，这说明了电路的通用性。

我们还介绍了一个至关重要的框架：语言 和 证人。 这是思考问题的一种不同的方式。 现在看来可能有点奇怪，但它是一套用于形式证明的强大工具。 我们将在以后使用语言，但就目前而言，只要将它们的存在记在脑海中就足够了。

如果你在经历了所有这些恶作剧之后还在这里，恭喜你！ 这可能是该系列中 最难的理论飞跃。 当然，我们稍后需要讨论其他理论概念，但至少对我来说，这是最难写，甚至是最难理解的部分。

所以下次，我们将开始建立在我们迄今为止介绍的所有基础之上，使用一些可能感觉更熟悉，但有助于使可验证计算和 ZK 系统真正可用的想法。

在那之前！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～