零知识证明 - Coda SNARK挑战（Stage1）

「 最近事情有点多，没怎么写文章。最近好多朋友都在关心我，有没有参加Coda举办的零知识证明的挑战？必须的。不光为了奖金，整个挑战的内容本身也是好的学习材料。不光是我，整个团队都在梳理理论，GPU实现优化，小伙伴们都太给力了:)

说个题外话，最近和一位好朋友聊天。聊到公司的创建和规划，她的经验我觉得很多初创公司可以借鉴：公司的创建和发展靠制度。公司的成长不是靠人情/感情维系，应该由公司体制/制度让公司的每个人清晰连接，彼此信任，一起努力让公司的目标实现。 」

前几个星期，由Coda以及Dekrypt资本发起一项挑战：The SNARK Challenge，通过GPU或者CPU指令集优化SNARK（Groth16算法）生成时间。时间从5/20号到7月15号。这项挑战也由Tezos，Filecoin，ZCash，0x等项目赞助。总奖金为10w美金。https://coinlist.co/build/coda。

此次SNARK挑战分为两期：第一期基础知识挑战（5/20～6/03），第二期是正式挑战（6/03～7/15）。此次挑战内容本身就是学习SNARK的好的教程。

第一期（Stage1）的基础知识挑战是整个挑战活动的热身，总奖金为200美金。挑战又分为四小题。

https://codaprotocol.github.io/snark-challenge/tutorial.html

01 第一题 - 域计算（大数模乘）

要求：使用GPU将素数阶域的元素数组相乘。给定一个域上的n组数，计算相乘的结果。两个域分别为 $\Bbb F MNT4753$以及$\Bbb F MNT6753$。

https://codaprotocol.github.io/snark-challenge/MNT4753.html

https://codaprotocol.github.io/snark-challenge/MNT6753.html

SNARK证明所需要的基本操作是乘法和加法。大数计算的位数比一般的计算使用的32位和64位要大的多。MNT4753和MNT6753的数为753位，也就是需要最少96个字节表示。753位，可以采用12个64位整数或者24个32位整数表示。其中的64位整数或者32位整数称为“limb”。

$\Bbb F q$的域由$0,1,...,q-1$组成。在这个域中可以进行加减乘除。以加法为例，a,b为$\Bbb F q$的两个数，则定义$a*b\ mod\ q$为a乘以b的结果。

大数模乘，要先介绍一下蒙哥马利表示：

一个大数x的蒙哥马利表示为$x*R\ mod\ q$。如果$R=2^{768},x=5$，则蒙哥马利表示为$5×2^{768}\ mod\ q$。

大数模乘，采用蒙哥马利规约（Reduction）算法（14.3章节）。

http://cacr.uwaterloo.ca/hac/about/chap14.pdf

假设m是个正的整数，R和m互质，并且$R > m,0\leq T < mR$。蒙哥马利规约算法能高效的计算：$TR^{-1}\ mod\ m$。

蒙哥马利规约算法的好处在于，如果$0\leq x,y < m$，$\widetilde x =xR\ mod\ m$，$\widetilde y =yR\ mod\ m$，也就$\widetilde x,\widetilde y$是$x,y$的蒙哥马利表示。则计算$xyR\ mod\ m = \widetilde x\widetilde yR^{-1}\ mod\ m$。

蒙哥马利规约算法的计算思路如下：

假设$m'=-m^{-1}\ mod\ R$，并且$U=Tm'\ mod\ R$，则$(T+Um)/R$肯定是个整数，并且$(T+Um)/R=TR^{-1}(mod\ m)$。因为$U=Tm'+kR,m'm=-1+lR$，所以

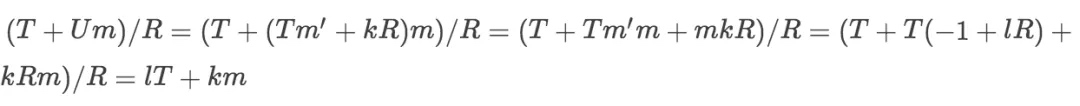
也就是说，要计算$TR^{-1}(mod\ m)$，可以通过计算$(T+Um)/R$获取。

如果$R=b^n$的话，除以R只要通过数的右移即可。14.32和14.36分别给出了一个大数，以及两个大数的蒙哥马利规约的计算算法：

02 第二题 - 二次扩展

在$\Bbb Fq$的域上进行扩展，增加一个“虚”部（有点像虚数的i），只是这个“虚”部是13的平方根。也就是二次扩展定义为：$\Bbb Fq[x]/(x^2=13)$。那就在这个二次扩展的域上的点表示为: $a_0+a_1x$，其中$a_0,a_1$都是$\Bbb Fq$域上的两个点。为了简单表示，二次扩展表示$\Bbb Fq^2$，因为二次扩展的域上有$q^2$个点。

二次扩展域上的加法和乘法定义为：

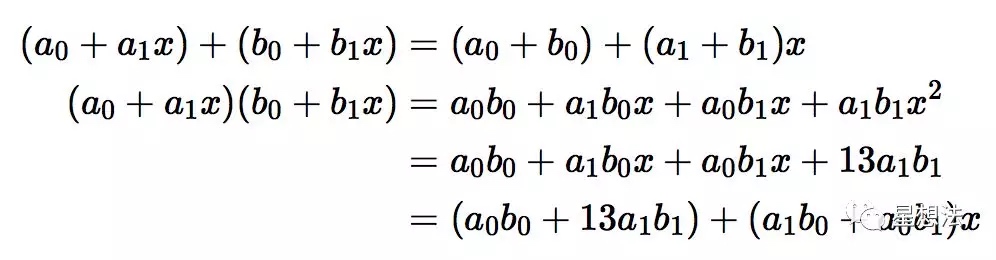
可以看出，二次域上的加法和乘法也是有一系列的大数乘法和加法组成。

03 第三题 - 三次扩展

和二次扩展类似，三次扩展定义为：$\Bbb Fq[x]/(x^3=11)$。那就在这个三次扩展的域上的点表示为: $a_0+a_1x+a_2x^2$，其中$a_0,a_1,a_2$都是$\Bbb Fq$域上的三个点。为了简单表示，三次扩展表示$\Bbb Fq^3$，因为三次扩展的域上有$q^3$个点。

三次扩展域上的加法和乘法定义为：

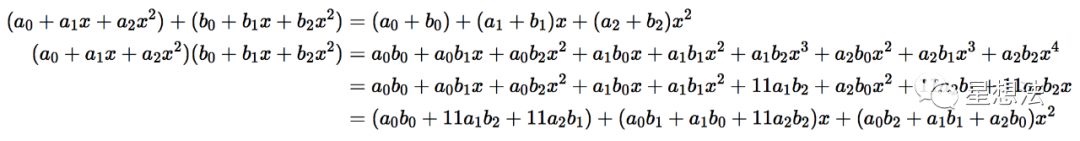
可以看出，三次域上的加法和乘法也是有一系列的大数乘法和加法组成（只是更复杂些）。

04 第四题 - 椭圆曲线群运算

椭圆曲线的定义：在一个域$\Bbb Fq$上，满足$y^2=x^3+ax+b$的点(x,y)组成一条椭圆曲线。椭圆曲线上的群运算（加法）定义：已知椭圆曲线P和Q，因为椭圆曲线有且只有三点在一条直线上，所以定义P+Q+R=0（0代表无限远点），也就是P+Q=-R。R为椭圆曲线上一条P和Q通过的直线的另外一个点。

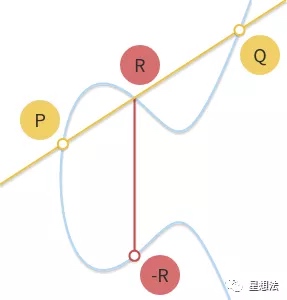
由椭圆曲线的方程，以及P/Q的直线方程，可以推导出（注意p和q的x相等的话，下面的公式不成立）：

var curve_add = (p, q) => {
 var s = (p.y - q.y) / (p.x - q.x);
 var x = s*s - p.x - q.x;
 return {
 x: x,
 y: s*(p.x - x) - p.y
 };
 };

http://www.hyperelliptic.org/EFD/g1p/auto-shortw-projective.html

在雅可比坐标系下，引入了Z坐标，线性坐标（x，y）可以变换成（X，Y，Z），满足：

 x=X/Z
 y=Y/Z

在点的Z坐标取值是否等于1的情况下，有不同的优化计算公式。以Z不等于1的情况下为例，计算公式如下：

 Y1Z2 = Y1*Z2
 X1Z2 = X1*Z2
 Z1Z2 = Z1*Z2
 u = Y2*Z1-Y1Z2
 uu = u2
 v = X2*Z1-X1Z2
 vv = v2
 vvv = v*vv
 R = vv*X1Z2
 A = uu*Z1Z2-vvv-2*R
 X3 = v*A
 Y3 = u*(R-A)-vvv*Y1Z2
 Z3 = vvv*Z1Z2

这样在雅可比坐标系下，点加的计算只需要乘法/加法/减法。只有当从雅可比坐标系转换回线性坐标系的时候，才需要Z的逆（$Z^{-1}$)。

总结：

Coda SNARK挑战的Stage1阶段介绍了SNARK算法的基础，大数算术（大数模乘）以及椭圆曲线群运算。SNARK挑战的本身也是很好的入门学习SNARK算法的好教材。