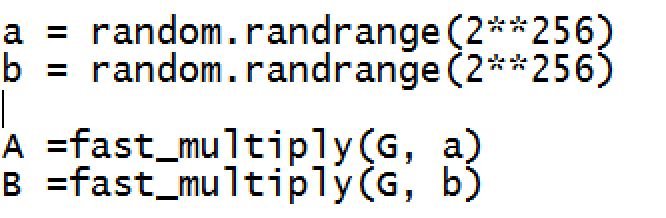椭圆曲线密码学的奇妙世界
- 密码学从头学
- 发布于 2024-07-15 21:54
- 阅读 4316
椭圆曲线密码学的应用:密钥交换与信息签名
原文链接:https://medium.com/coinmonks/the-wonderful-world-of-elliptic-curve-cryptography-b7784acdef50
介绍
那么,什么比互联网上的任何其他东西更能保护你的隐私和安全呢?那将是椭圆曲线,尤其是:
$$y² = x³+ax+b$$
其中 4a³+27b² ≠ 0(需要避免奇点 )。最流行的曲线是 Secp256k1(或 Curve 25519),定义为 a=0 且 b=7:
$$ y² = x³+7 $$ [链接 ]
在这里,使用 ECC(椭圆曲线密码学),我们取一个随机数(n),以及椭圆曲线上的一个点(G),然后将它们相乘以产生 P:
$$ P = n G$$
$G$ 将是曲线上的一个$(x,y)$点,Bob 和 Alice 都知晓。n 将是 Bob 的私钥,P 将是他的公钥。挑战在于,如果 n 是一个 256 位的随机值,即使我们知道 G 和 P,找到这个值也将非常困难。
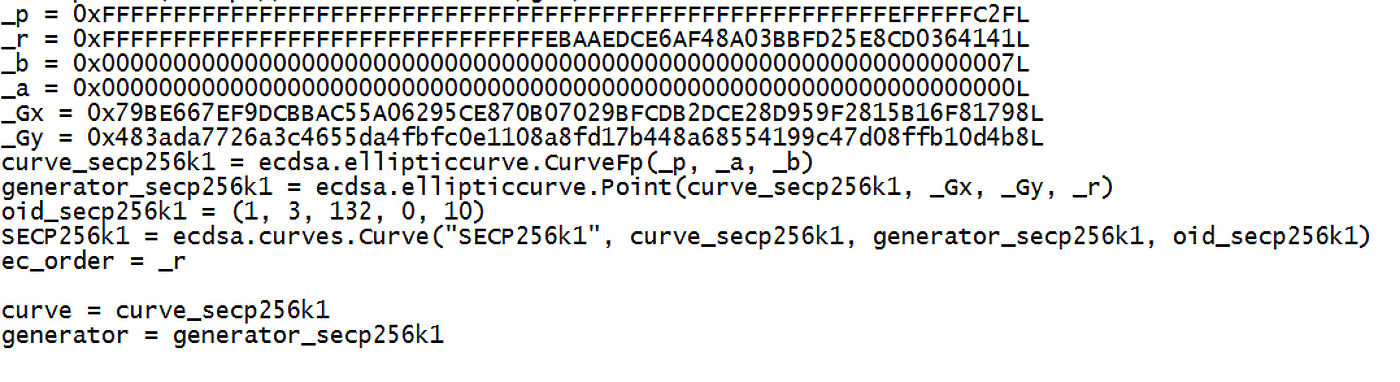
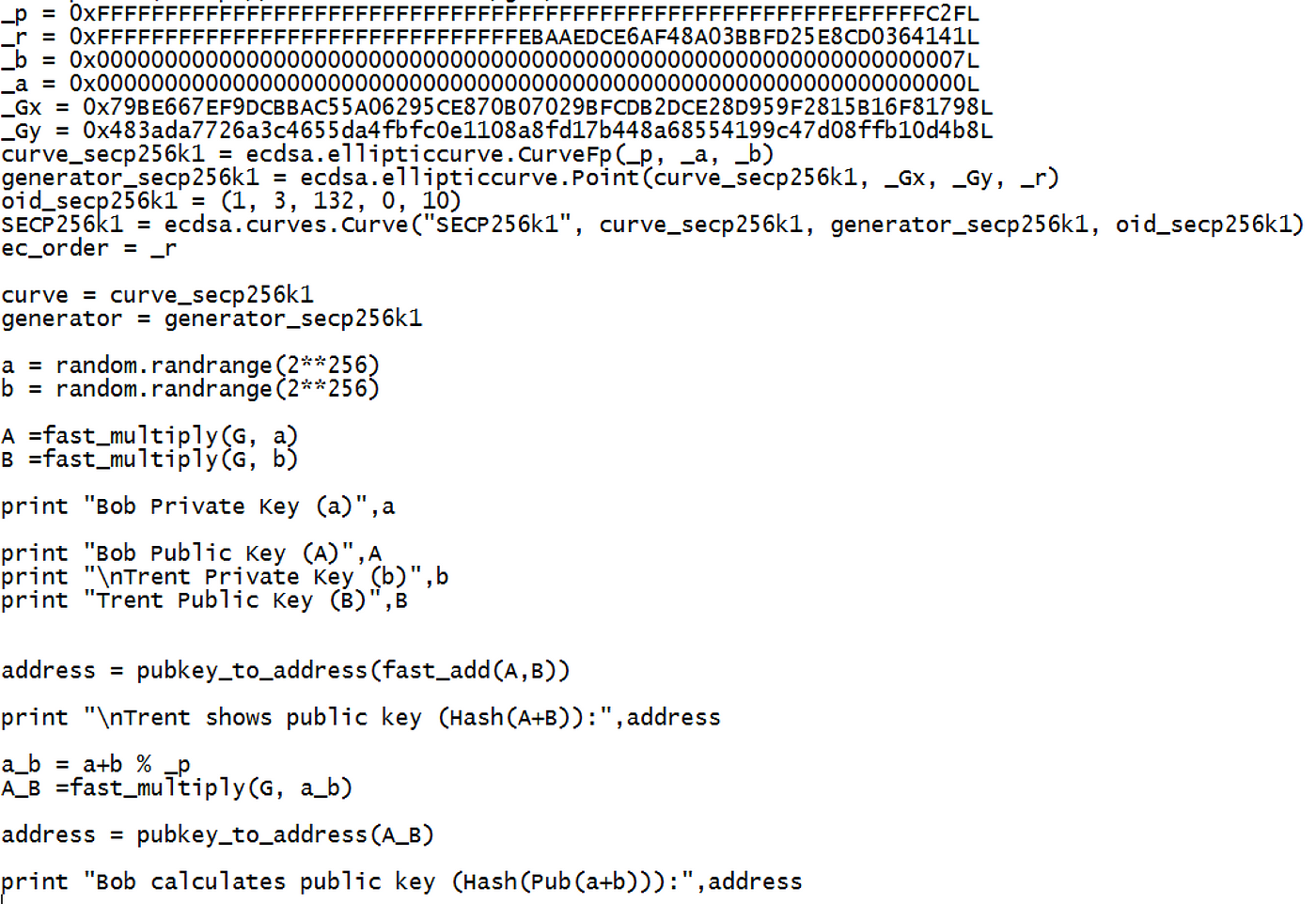
因此,让我们看一下 Python 代码,设置一个椭圆曲线:
在这种情况下,我们看到_a 为 0,_b 为 7(y² = x³+7),我们有一个_Gx 和一个_Gy 值。我们还有 _p,这是一个素数,所有操作都是通过(mod _p)函数进行的。在 Python 中,我们可以为 Alice 和 Bob 创建两个密钥对:
我们生成一个随机的 256 位值作为 a,然后通过与 G 相乘找到公钥(A)。这将给我们一个椭圆曲线上的点。请注意,所有操作都是使用(mod _p)进行的,其中 mod 运算符是整数除法的余数。
分析密钥
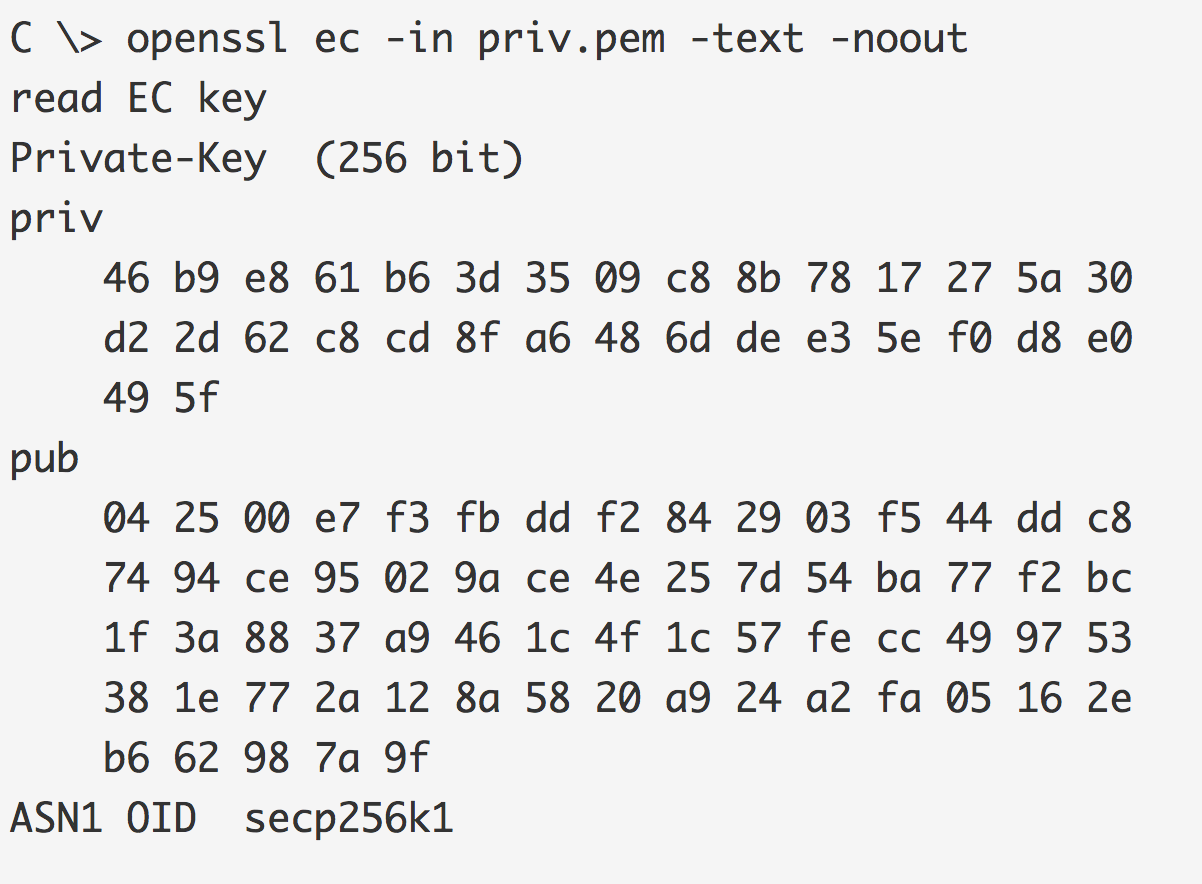
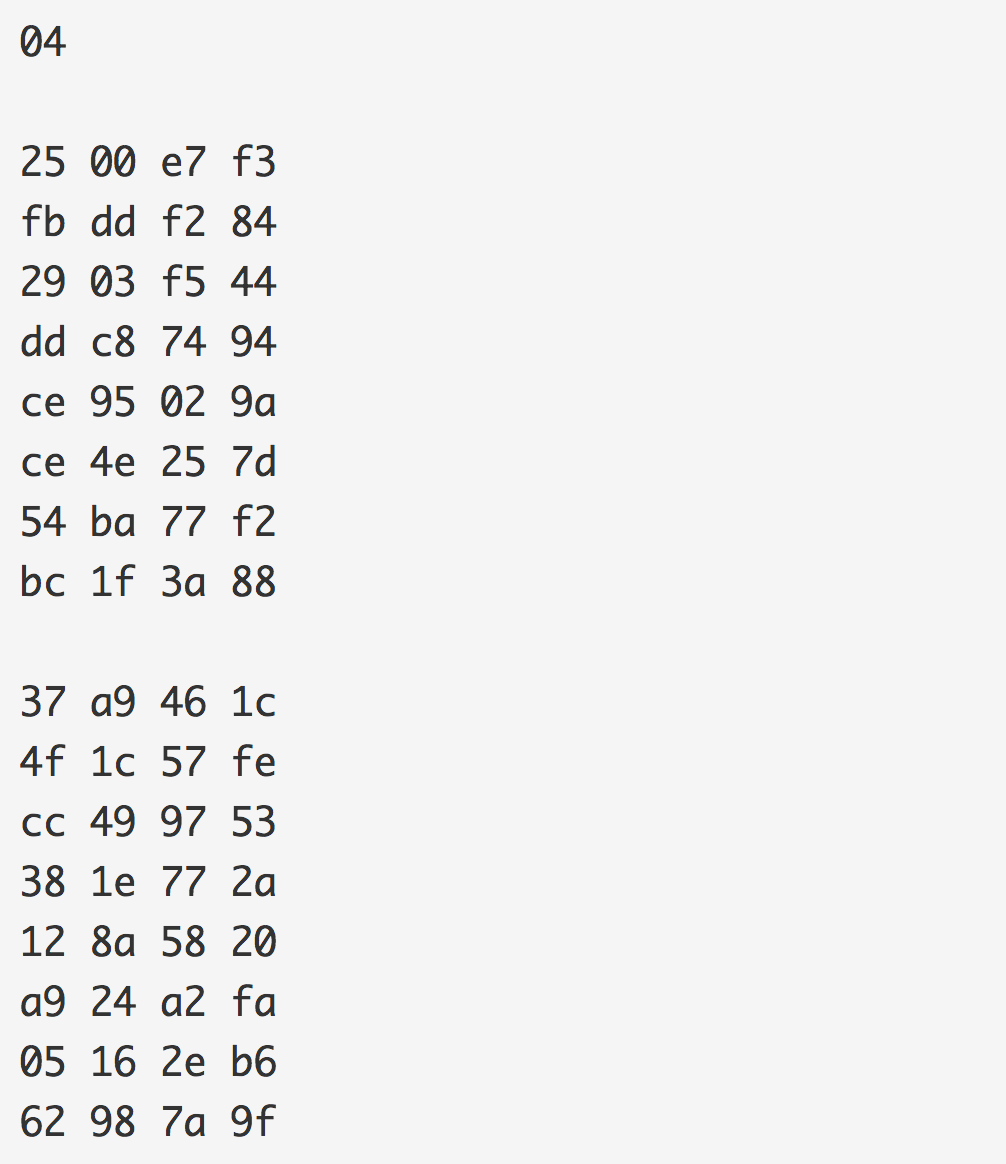
当我们使用 Openssl 生成密钥对时,我们会看到一个 256 位的私钥(由 32 字节组成),以及 65 字节的公钥。公钥开头的 04 是一个标识符。定义公钥的两个 256 位点(每个点都是 32 字节长):
在这种情况下,私钥是:
公钥是:
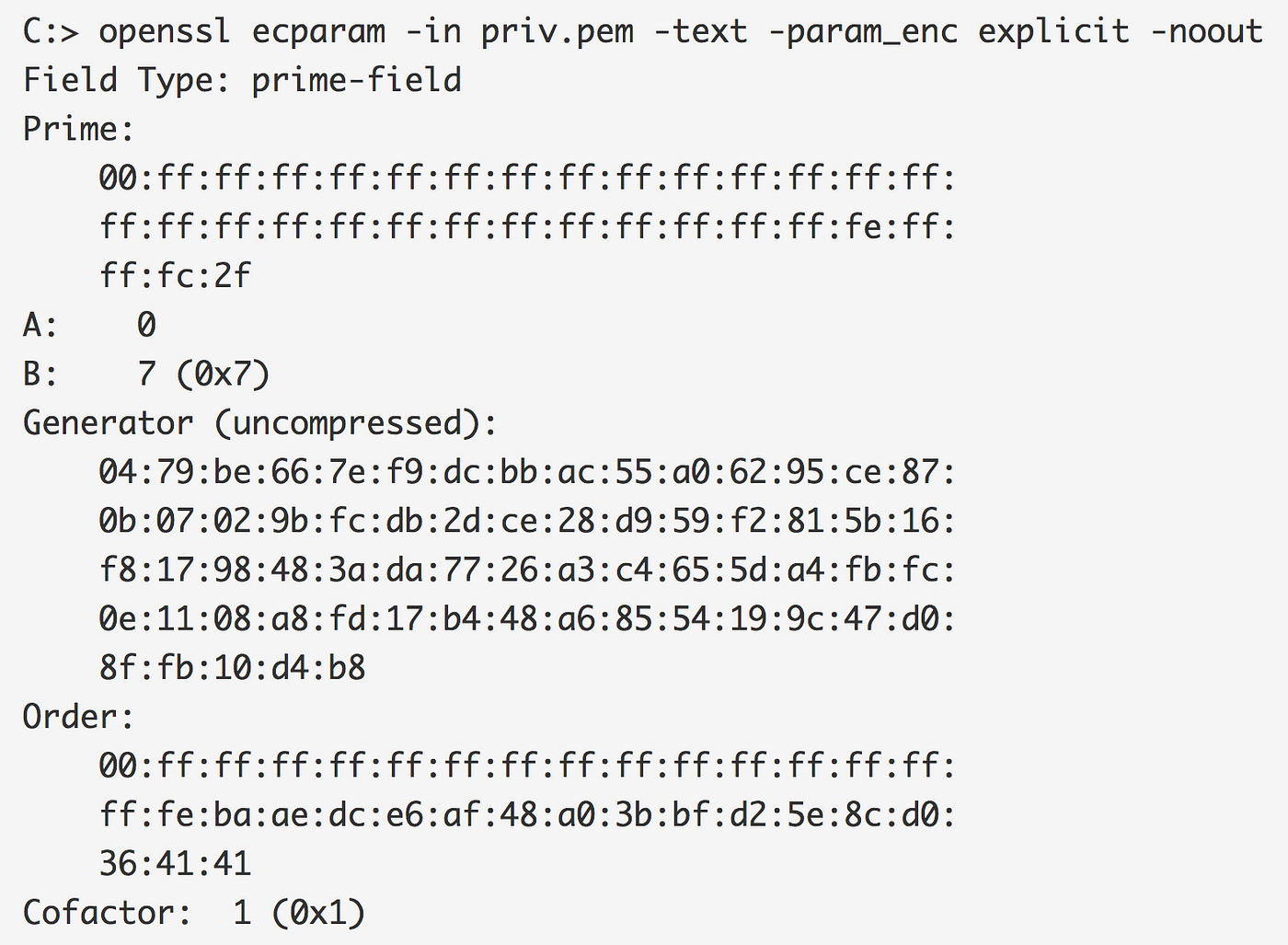
可以查看共享的椭圆曲线参数:
请注意,这里的素数、A、B 和生成器的值与上面 Python 片段中的_p、_a、_b、_Gx 和_Gx 的值相同,对于此曲线标准的任何应用可能是相同的。如果你感兴趣,一些曲线参数的标准定义在这里 。
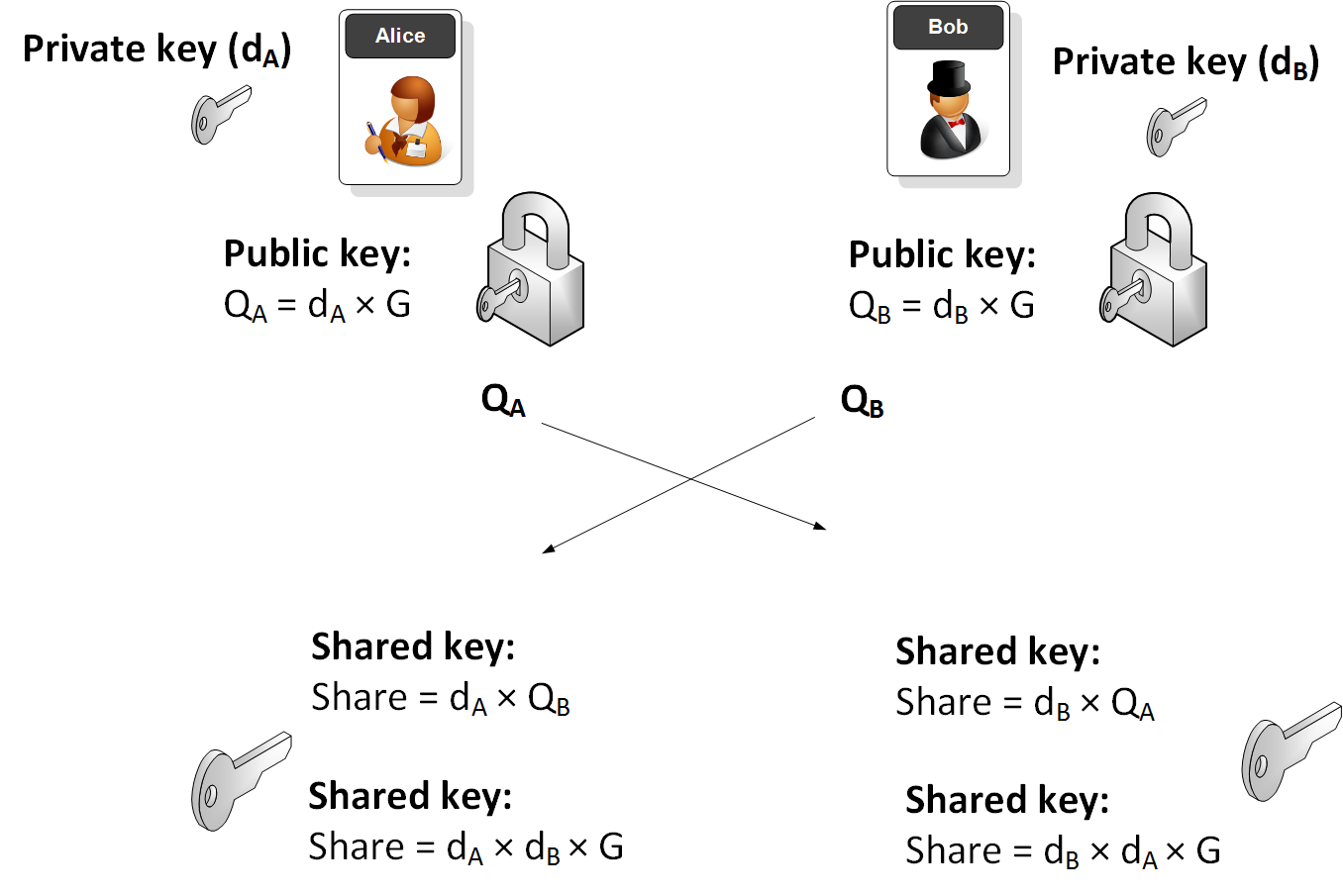
ECC 应用 — 密钥交换
ECC 的两个主要应用是数字签名和密钥交换。在密钥交换中,我们可以采用类似于常见的 Diffie-Hellman 方法的方法:ECDH。使用此方法,Bob 和 Alice 都生成他们的密钥对,然后交换他们的公钥值。接下来,他们将这些值分别与自己的私钥相乘,应该得到相同的点。点的 x 值通常用作共享值,可以用来生成加密密钥[链接 ][实际示例 ]:
一个简单的例子是[链接 ]:
基点:(920(mod 3851),303(mod 3851))
Alice 的私钥:25720
Bob 的私钥:15297
\==========================
Alice 的公钥:(1996(mod 3851),3624(mod 3851))
Bob 的公钥:(94(mod 3851),884(mod 3851))
\==========================
Alice 的共享密钥:(2636(mod 3851),3251(mod 3851))
Bob 的共享密钥:(2636(mod 3851),3251(mod 3851))
\==========================
共享值是 x 值:2636
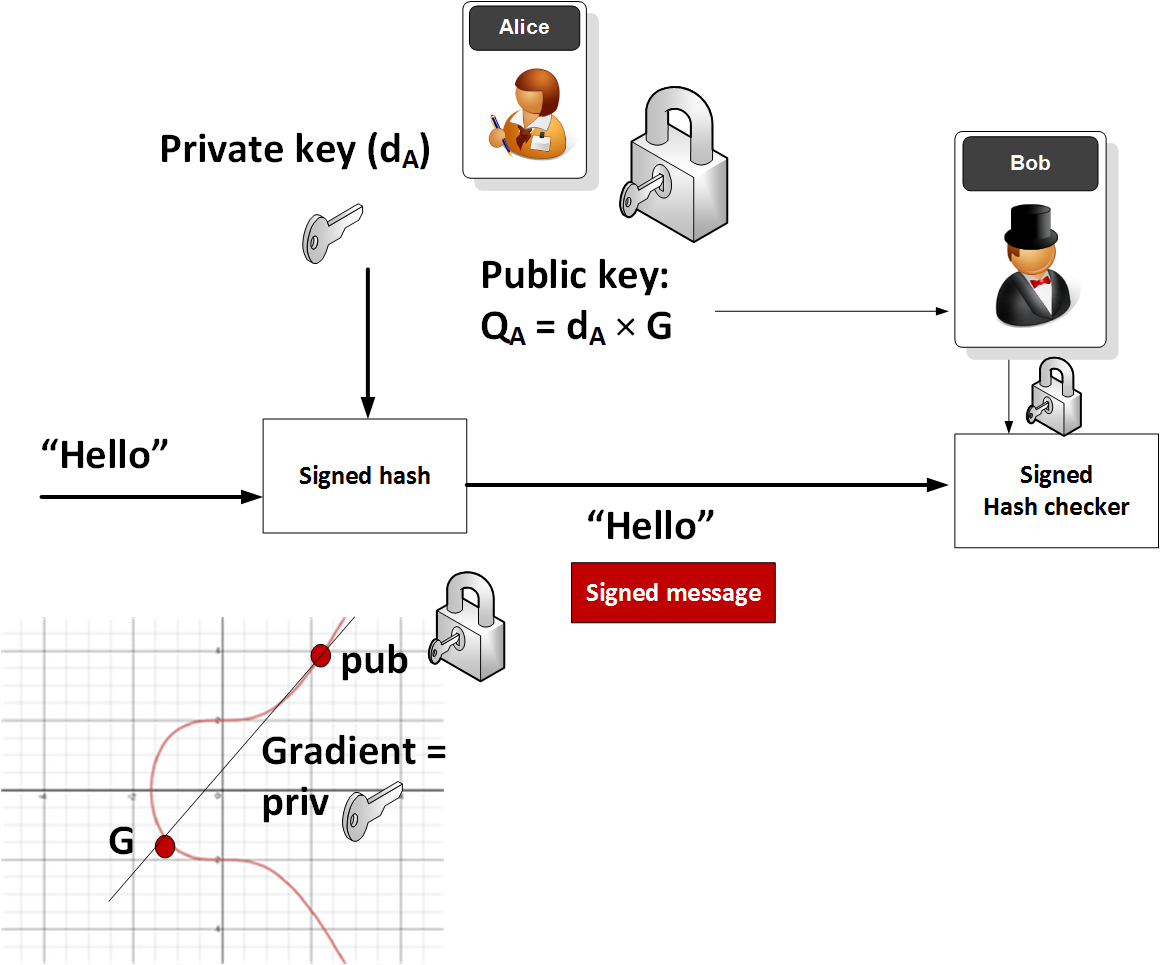
ECC 应用 — 数字签名
ECC 的另一个应用是签名,例如椭圆曲线数字签名算法[这里 ]。使用此方法,Alice 将生成一个密钥对,然后使用她的私钥加密消息的哈希值。然后,她将消息和签名的哈希发送给 Bob,Bob 对消息进行哈希,并用 Alice 的公钥解密 Alice 的哈希版本。如果哈希匹配,他就证明了 Alice 发送了消息,并且消息没有改变:
比特币地址和签名
椭圆曲线在互联网、智能卡和物联网应用中随处可见。你还可以在区块链中看到它,区块链中使用它作为标准方法来签署交易。使用此方法,Bob 有一个钱包,其中包含他的公钥和私钥。私钥用于签署他的交易,公钥将证明他是签署者。我们还从密钥对生成 Bob 的 ID。
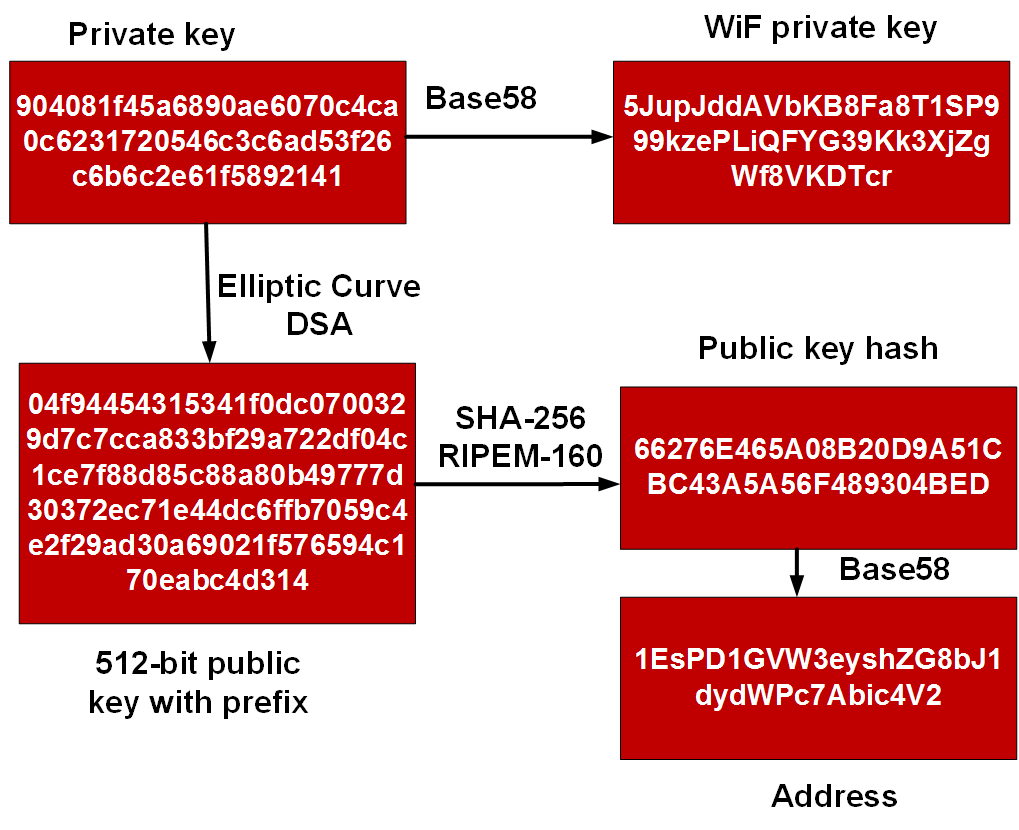
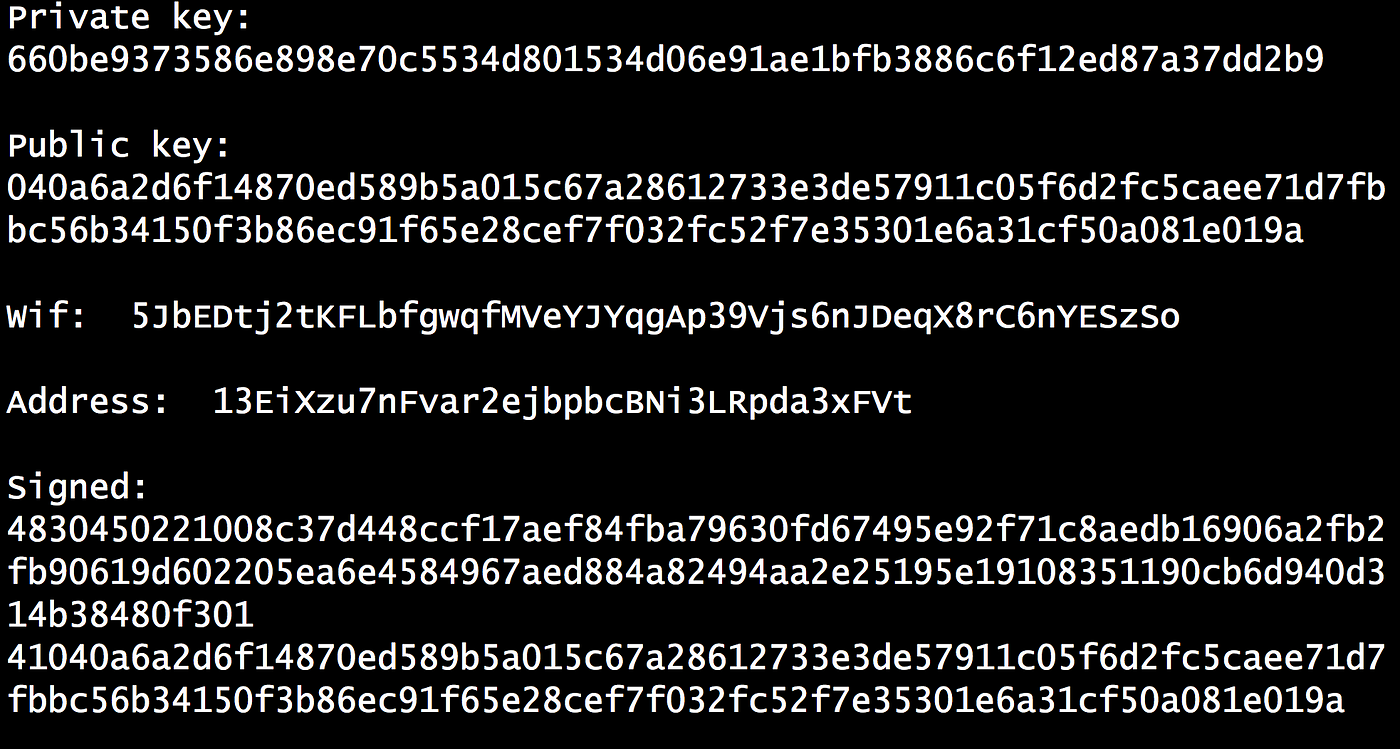
为此,Bob 最初创建一个 256 位值,这将是他的私钥。该密钥转换为 Base-58 形式(去除难以区分的字符,如'O'和'l'等[这里 ])。这是他的 WiF(钱包互换格式)私钥。他不应该向任何人透露这一点,并且如果可能的话,不应该将其存储在线。接下来,他将生成他的 512 位公钥(如上所示)。然后,将其使用 SHA-256 和 RIPEM-160 进行哈希处理,以生成公钥哈希值。然后,使用 Base-58 将其转换为 Bob 的比特币 ID:
一个示例:
因此,如果我们想向 Bob 发送比特币,我们只需要获取他的地址,然后用我们的公钥签署交易。
添加点
我们知道如何通过标量值(私钥)将我们的椭圆曲线上的点相乘,但是我们可以将点相加吗?如果我们取两个点:
P1 = n G
P2 = m G
如果我们将这些点相加,我们得到:
P1 + P2 = n G + m G = (n + m) G
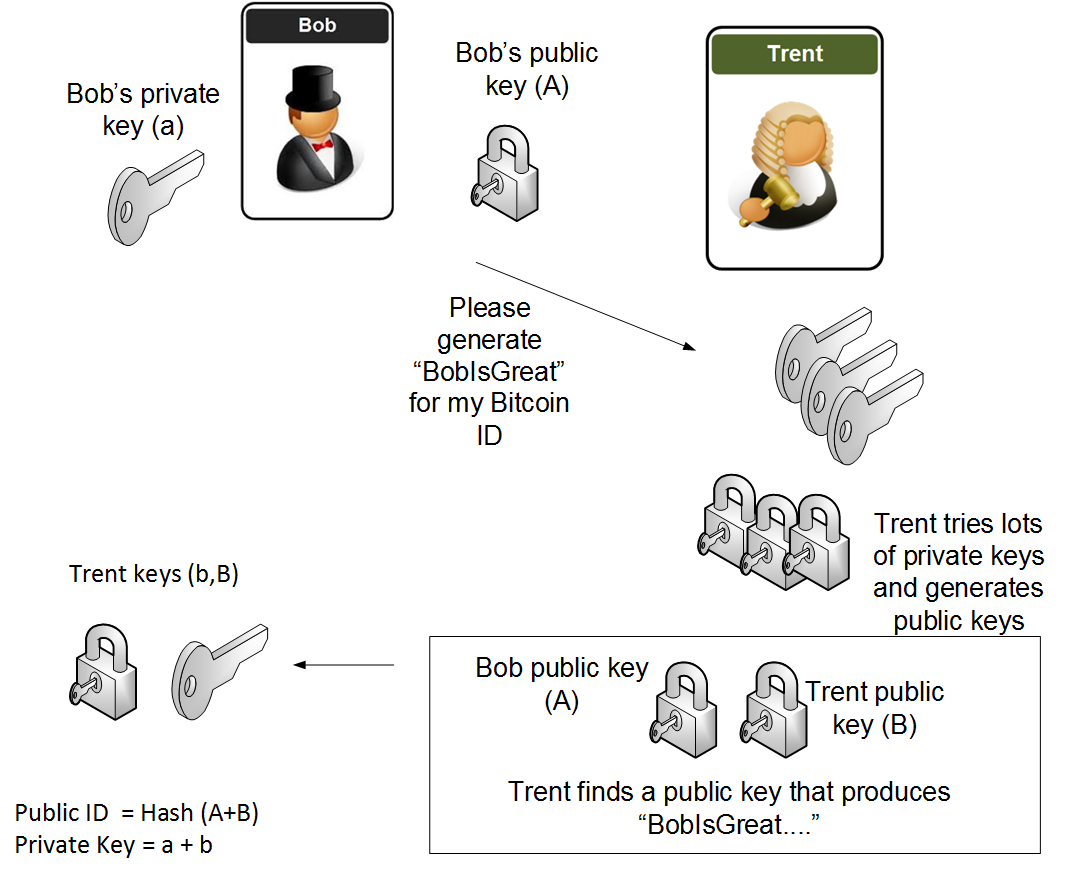
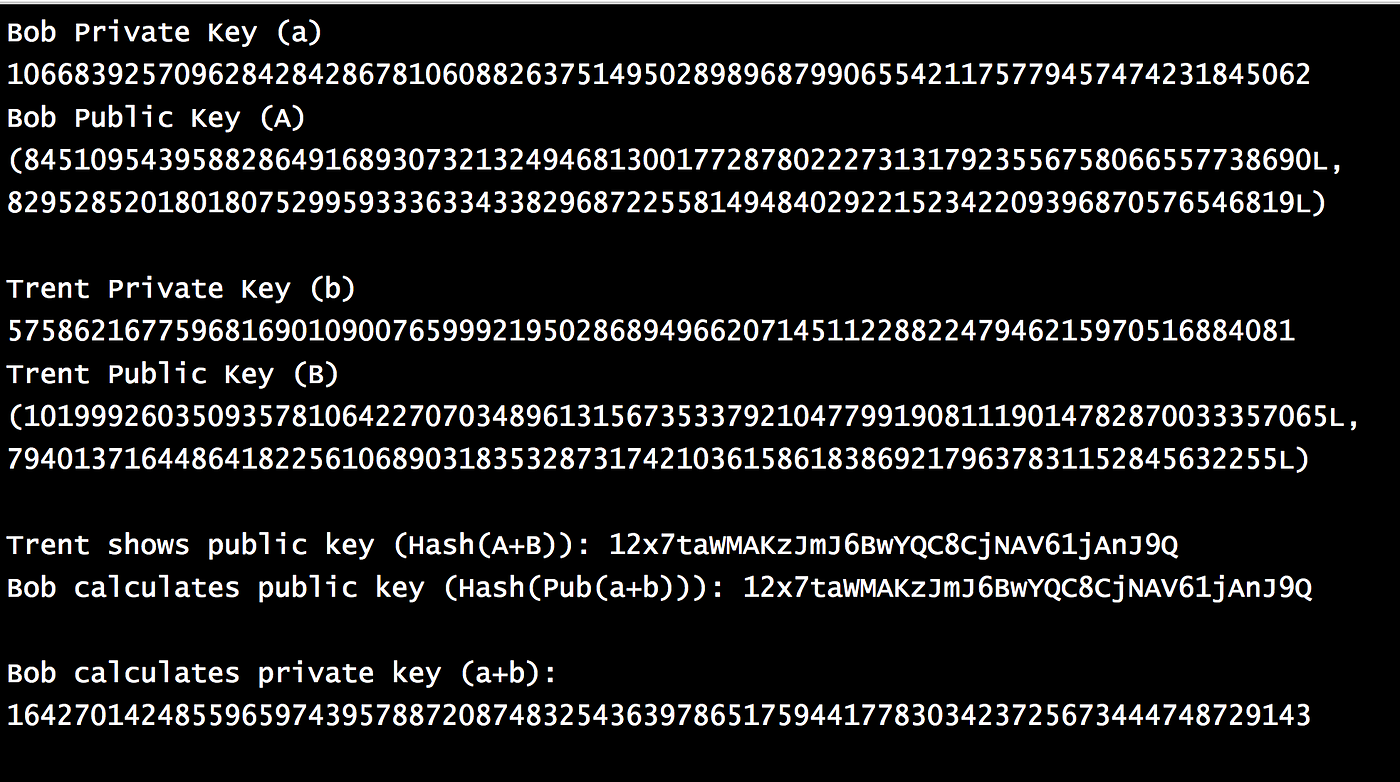
因此,如果我们添加公钥(P1 + P2(mod p)),等效的私钥将是(n + m(mod p))。如果 Bob 有一个私钥(a)和一个公钥(A),然后 Trent 有一个私钥(b)和一个公钥(B)。那么公钥将是 A+B,私钥将是 a+b。以下是一个示例[这里 ]:
程序是 Trent 生成一个密钥,Bob 可以使用它来生成等效的公钥:
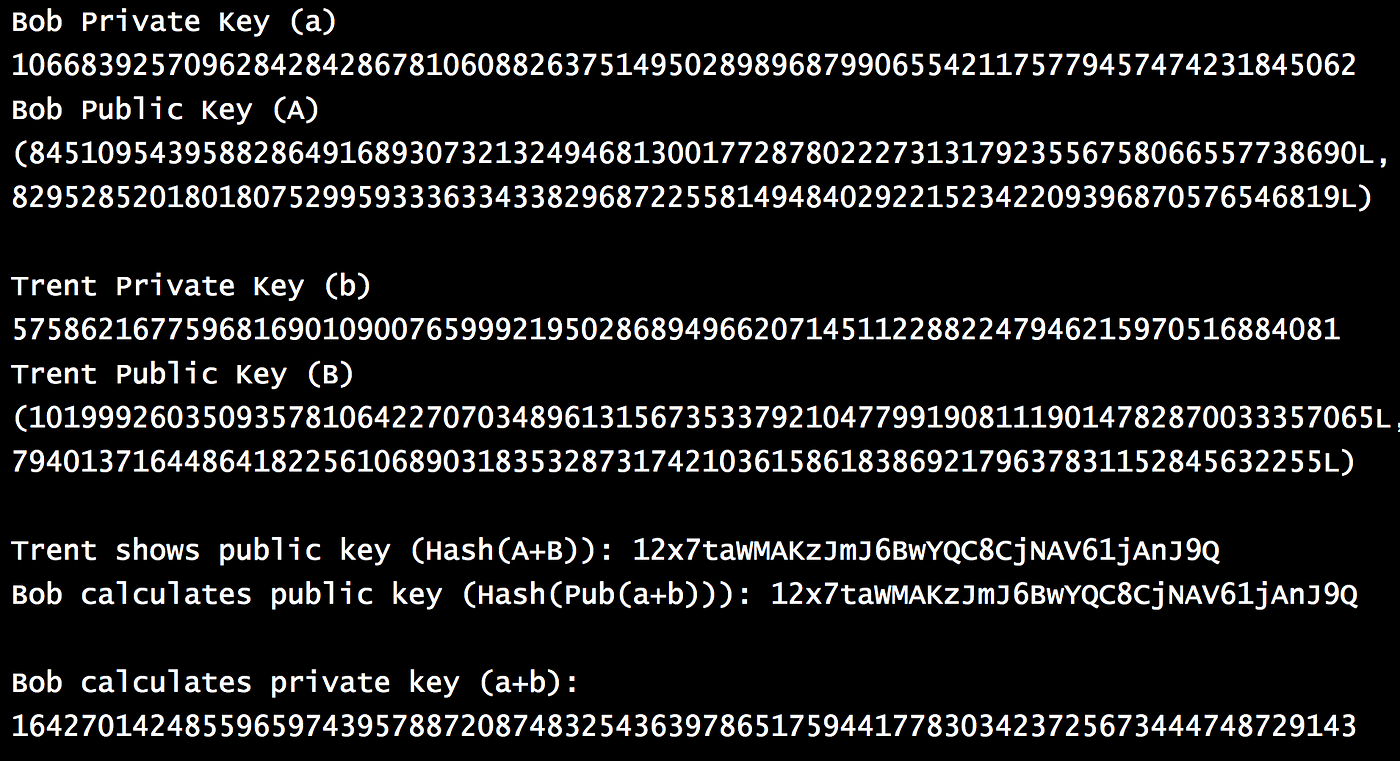
使用从比特币库中获取的 fast_add()和 fast_multiply(),我们可以实现如下:
一个示例运行是:
BN 曲线上的密钥配对
椭圆曲线在公钥加密中被广泛使用(例如比特币和 Tor)。 BN 曲线(Barreto-Naehrig curve)[paper] 定义了一个椭圆曲线,可用于支持高安全性和效率的配对。本页面使用 256 位 BN 曲线上的配对,并为消息生成签名。椭圆曲线密钥配对还与 zk-SNARKs 和零知识证明一起使用。它可用于“加密乘法”。
对于椭圆曲线,我们为私钥(p)生成一个 256 位的随机数,然后取椭圆曲线上的一个点(G)[x,y],然后将其乘以私钥以获得另一个点(p×x,p×y)。通过这种方式,我们得到 P=p×G,其中 G 是椭圆曲线上的一个已知点,P 是我们的公钥,p 是我们的私钥。
通过配对,我们可以在点之间推导出更复杂的关系,例如如果 P=G×p,Q=G×q 和 R=G×r,我们可以检查是否 r=p×q,但我们只知道 P、Q 和 R(公共值)。目前我们无法从 P=p×G 计算 pp,即使我们知道 P 和 G。值的暴露受限于我们可以计算 R=G×p×q,但无法确定 p 或 q。
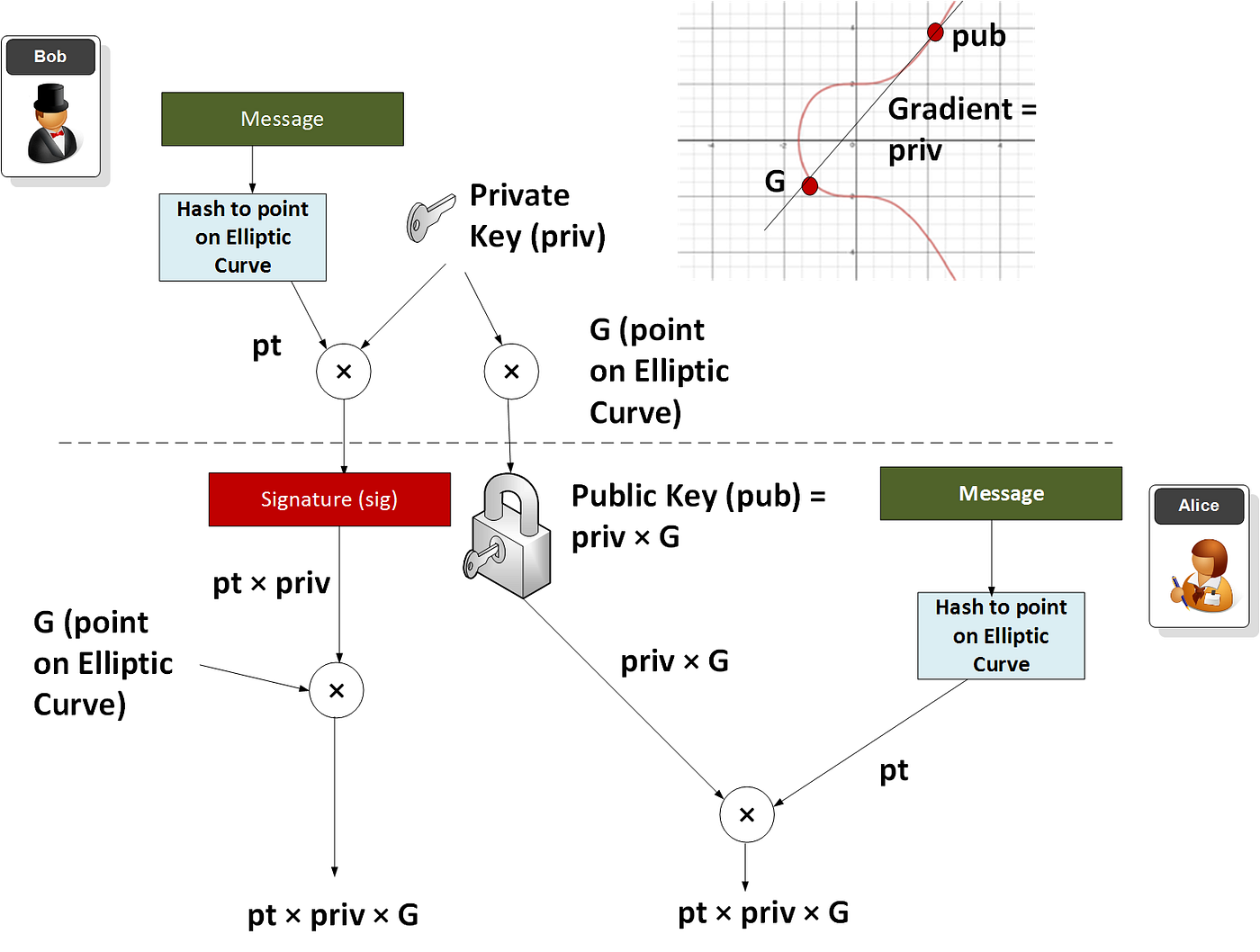
以下代码集成了 BN-256 代码。让我们通过简单地为消息创建一个签名来测试代码。Bob 将获取一条消息并使用他的私钥创建一个签名,Alice 将使用他的公钥来验证。
首先我们将消息哈希到椭圆曲线上的一个点(pt)。接下来我们取私钥(priv)— 一个随机的 256 位值 — 并将点乘以 priv 以给出 priv×pt。这就是签名。然后 Bob 通过将他的私钥(priv)乘以 G 来生成他的公钥以给出 priv×G。Alice 然后将消息哈希到椭圆曲线上的一个点(pt)。接着她将此点乘以 Bob 的公钥以得到 pub×pt。她还将签名(sig)乘以 G 以得到 sig×G。如果签名正确,生成的两个值应该匹配[here]:
结论
椭圆曲线加密是魔法!
- 零知识编年史:群 109 浏览
- 以太坊签名方案解析:ECDSA、BLS、XMSS 以及带 Rust 代码示例的后量子 leanSig 493 浏览
- 论“高保证”密码学的承诺 374 浏览
- 使用 Ecash 票据的谨慎日志合约 415 浏览
- Fiat-Shamir 启发式非交互式零知识证明之美(以及 Zig) 656 浏览
- Zig 签名(Ed25519 和 ECDSA) 1373 浏览
- DahLIAS:既非 ECDSA,也非 Schnorr 625 浏览
- ECDSA确定性签名 1160 浏览
- 门限方案攻击:第二部分 820 浏览
- 以太坊智能合约中的数字签名 2068 浏览
- 安全研究人员的数学指南 942 浏览
- 构造与破解SIDH 1301 浏览