BLS签名实现阈值签名的流程

BLS （Boneh-Lynn-Shacham）签名算法是一种可以实现签名聚合和密钥聚合的算法，它可以把一笔交易中的所有签名和公钥合并成单个签名和公钥，且合并过程不可见（无从追溯这个签名或公钥是否通过合并而来）。

原创说明：BLS签名在英文文档介绍的比较多，但是很多讲得并不清楚，通常需要查看原有的论文，对应后学习，对一般的程序员要求比较高。这里整理了一下本人在学习bls签名过程中的详细推导过程，自认为比较容易理解一些。跟大家共享一下，也是为墨客的随机数子链做一些技术层次的科普铺垫。在阅读本文的内容前，读者可以先简单复习一下常见的椭圆曲线公私钥生成算法，用来对比BLS，会有助于理解本文的内容。

1.基本原理

先简单介绍一下BLS签名。BLS的签名采用曲线对的方式可以验证两个（或者同一个）曲线上的点对符合乘法交换律：

e(P, Q) → n
e(x×P, Q) = e(P, x×Q)

在BN曲线上面可以表示成：

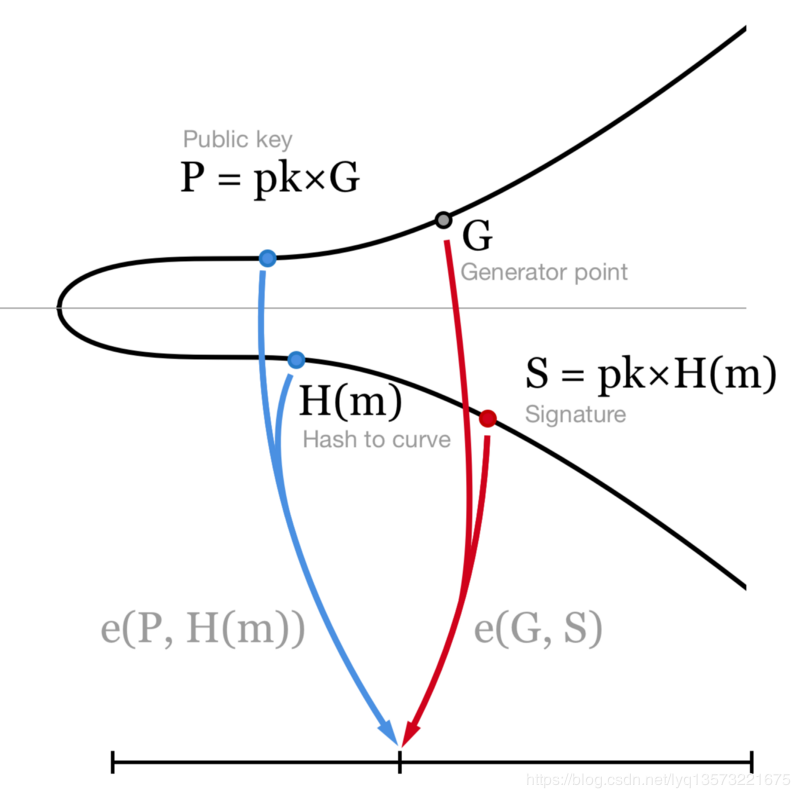
（来源于：cryptoadvance）

与传统的椭圆曲线不同，BLS的创新点在于让hash H(m)也能够对应于BN曲线上的一个点。这个映射空间大致是2：1的关系，可以很容易的处理。实现细节不重要，就当个结论记一下。 另外，简单起见，本文里面提到的BLS签名和阈值签名不做区分。

阈值签名（threshhold sig）本质是m-of-n的签名方式，在知道m个签名的条件下，可以合成唯一一个合法的签名。任意m个签名片段的组合都是同一个可验证的签名。而且，由于每个人只有一个私钥片段，需要m个私钥片段组合在一起才能形成一个合法的完整的私钥。如果少于m个私钥片段在网络中共享的话，就不会有任何一个个人知道这个完整的私钥。

博客还有另一遍文章介绍阈值签名，有兴趣可以阅读。

这里最基本的数学原理其实很简单，就是利用m个变量的多项式方程在m个条件下可解。如果系统中有n>m个条件，任意m个条件都可以得出一个唯一确定的解。当然，如果小于m个条件就不可解。

2.主要流程

这里首先涉及到一个可验证私钥片段分发的问题（VSS）。每个节点独立产生自己的私钥片段，然后将可验证的公钥广播出去，以及系统中其他节点需要验证本地节点的可靠性的信息。这个公/私钥片段分发验证的过程在初始化阶段做一次即可（除非节点数变化，则再需要分发一次）。这个流程如下：

2.1 每个节点生成一组私钥

r_0, r_1, .., r_{m-1}

$r = a, b, c, d, ..$

这些私钥是一个m阶多项式的参数:

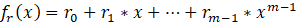
2.2 每个节点对其他节点x=1,2,…,n生成多个多项式的值， 最简单的情况就是用其他节点的编号。生成后在私底下秘密传递给相对应的节点（一般可以通过用对方的非对称公钥加密后发送）：

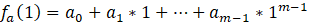
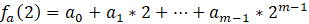
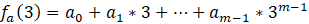
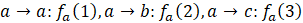
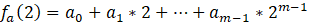
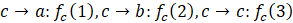
这样每个节点拥有n个共享私钥（用于解方程的条件）。这些私钥不能暴露给第三方。

2.3 每个节点公开公钥信息：

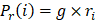
2.4 每个节点可以验证收到的$$f_r(x)$$是否正确，以a为例，验证方法为：

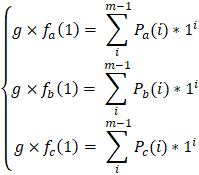
2.5 如果验证有错，广播错误，这里会涉及一些反馈以及contest的过程。

2.6 如果所有的节点的验证都没有错误，每个节点达成一致，每个节点本地获得的信息如下表：

2.7 这样，系统中的全局私钥为$$(a_0 + b_0 + c_0)$$，全局公钥为$$g\times (a_0 + b_0 + c_0)$$。但是没有一个人能够知道全局私钥。如果知道了m个共享私钥片段$$f_r(1..m)$$，就可以计算出全局私钥。

3.应用示例

有了这个基础，我们就可以实现第一个应用。

应用1：创建一个聚合私钥(m-of-n)，每个人有自己的私钥片段，只有在收集>m个私钥片段后，才可以得到全局私钥，来对全局公钥对应的钱包地址的操作进行签名。这个可以用来配置一些需要多方控制的钱包。

但是这里有个问题，因为在使用的时候，需要m个私钥片段的合成。这个过程可能会导致m个片段为公众知道，所以，这样的应用实用性不强，因为一旦大于m个私钥片段公布在网络中，任何一个人就可以算出来全局私钥，那么辛辛苦苦经历步骤1-6的过程只能使用一次，代价太大了。

这里，就需要用到BLS签名的长处了。具体的做法是，节点不应该公布共享私钥信息，而只是公布签名信息。这样，共享私钥可以一直使用，每个人可以验证签名的有效性。而全局私钥却没有人能够知道。这个就是threshold 签名。

具体的做法如下：

1、对于一个信息s，先计算出其hash在曲线上的映射$$H(s)$$，参见文章开头的插图 2、每个节点公布$$H_r(s)=\sum fr(i) \times H{(s)}$$ 3、这样任意m个$$H_r(s)$$可以计算出$$(a_0 + b_0 + c_0) \times H(s)$$，这个就是信息s的全局签名。

下面以具体的例子来说明。比如对于 m=2，n=3 的情况，如果已知两个节点的签名片段A，B： 节点1的签名片段A 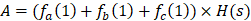节点2的签名片段B

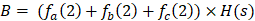
由：

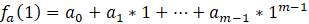
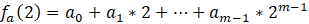
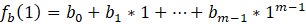
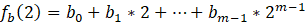
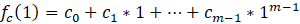
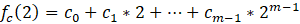
可以得到：

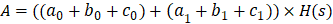
所以：

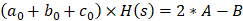
那么这里的阈值签名就是：

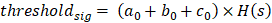
签名的数值就是公开的两个签名片段的数学运算：

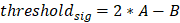
每个人都可以验证这个签名的合法性。注意，这里用到了前面提到的特性，就是H(s)也在曲线上面。这也是为什么BLS签名能够工作的本质。 验证：

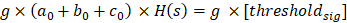
也即：

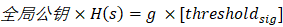
同样的，如果公布了节点1的签名片段A和节点3的签名片段C，阈值签名就应该是：

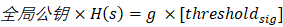
可以证明，这个签名和前面的是一致的。 由此，我们可以实现第二个应用。

应用2：创建一个随机数区块链，区块链的每个共识节点通过初始化实现VSS，每个节点有自己的私钥片段。然后每个节点对某个信息（交易集合，或者预定义信息）进行签名。节点在收集>m个签名片段后，就可以合成全局签名。这个签名可以很容易通过全面公钥来验证。在这个过程中，全局私钥没有任何人知道，但是这个签名的结果是多个节点认可的结果。如果以这个全局签名作为随机数源，这个随机数就是一个共识的结果，而且无法被单个人篡改。而且，这个是可以持续安全地产生随机数，只要每轮给出不同的信息来签名。

但是这里有个问题，如果每个节点公布签名片段的话，信息量是O(n2)，有没有更好的方案，请关注后续文章。

本文主要内容来自墨客区块链CEO陈小虎。