密码学入门：阈值签名

这是关于密码学的一系列更大文章的一部分。如果这是你遇到的第一篇文章，我强烈建议你从 这系列的开始 开始阅读。

在 上一篇文章 中，我们学习了多项式，并且看到了它们的一些应用。

然而，这篇新的密码学内容似乎与我们迄今为止学习的内容没有关联。然而，有一些很酷的方式可以将它们与之前的概念结合起来，例如 数字签名。

本文将专注于解释这样一个例子，其中我们将常用的 签名技术 与 多项式 结合起来，创建一个有趣的 混合方案。我们将以 椭圆曲线 为背景，使用 G 和 H 来表示一个群体 𝔾 的生成元。

我会松散地基于 这篇论文 进行解释，并作出一些调整，以期使事情易于理解。

仍然，友好的免责声明：阈值签名很难解释。我们需要澄清许多细微之处。因此，让我们先看一下它们是什么以及它们的作用的简要总结，然后再深入到其背后的数学。

足够的签名者

阈值签名 是一种 多签名 — 意味着需要多个参与者签署一条消息。但这一次，并不是每个参与者都必须这样做。

想象一下，一个拥有应用程序管理员权限的十人小组。为了执行某些敏感操作，我们需要 至少三个 批准。

这样，我们就不必同时打扰所有的管理员；只需要一个可用签名者的子集就足够了。

这感觉像是我们之前探讨的 多签名方案 的一次 升级，其中所有签名者都被要求参与。但实际上，实现这一结果涉及到一些更复杂的 密码学技巧。

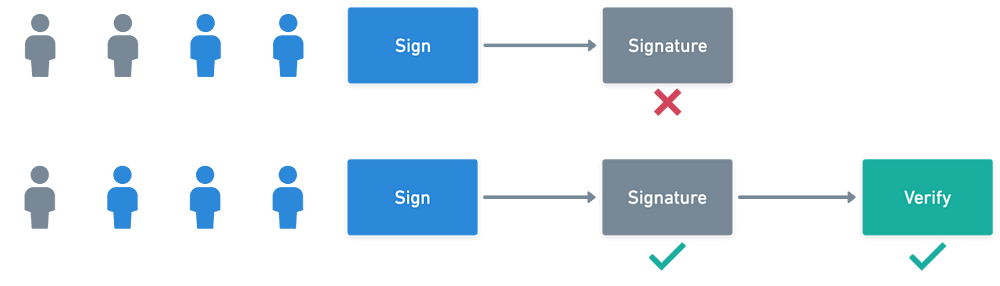
一个阈值签名，其中至少需要 3 个中的 4 个签名者

我们可以将阈值签名分为 三个主要步骤 或 算法（就像大多数签名方案一样）：

• 密钥生成（KeyGen），这是一个输出一个 共享 的 私钥 和 公钥 对的算法，
• 签名，处理消息与私钥和一个 随机数（nonce）以获得一对 (r, s)，
• 以及 验证，这是验证签名是否与消息和公钥相符的步骤。

在使用阈值签名方案时，密钥生成 和 签名 步骤，在过去的例子中相对简单，将被更复杂的过程取代，涉及签名者之间的 通讯。幸运的是，验证 仍然保持不变 — 因此我们的关注将放在前两步上。

请注意，要求一定数量的签名者的想法与重建 一个 多项式所需的最低点数量非常相似，借助 插值 可以实现 插值。事实上，这也是阈值签名工作的核心。

此外，为了保持内容的清晰，我们必须说签名者或参与者是 有序的。每个参与者将拥有一个 标识符 或 索引，范围从 1 到 n，即参与者的总数。

我们的目标已经设定，介绍结束。我们可以进入好戏了吧？

初步准备

在阈值协议中，共享信息 是关键。最终，一组签名者共享信息的能力将使他们能够生成签名。

我们已经看到，分享一个秘密可以通过 夏密尔秘密共享 （SSS）来实现。其思想是在许多不同的值上评估一个多项式，然后将结果作为 点 进行共享。并且有了这些点，我们可以 反插值 回原始多项式。

但这里有一个问题。任何接收者如何检查他们收到的值是否是 正确计算 的？换句话说，是否有办法 证明 这些点确实与原始多项式相关？

你可能会想，为什么 值会不正确？为什么会有人发送错误的值？这里有至少两个原因：通信中的错误 和 恶意活动。攻击者可能试图破坏我们的签名模型—我们不能指望每个人都能正确行为，因此我们必须采取措施来减轻这种可能情况。

为了应对这一担忧，我们需要一个 新工具。

可验证的随机秘密共享

我们所做的是要求共享者进行一个 承诺。这将 绑定 共享者与他们的秘密信息（多项式），以便后续他们不能生成无效值。

这个想法就是 可验证的随机秘密共享（ VRSS），这是一种可以替代 SSS 的方法。我们想做的是承诺我们多项式的 系数——为了做到这一点，我们需要的不是一个，而是 两个 个系数：

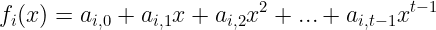
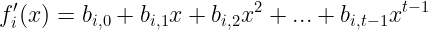
你问这是为什么？因为承诺需要 隐藏。我们不想暴露系数，因此它们的承诺应该是 盲化 的。第二个多项式的系数实际上就是这些盲化因子！

因此，通过使用我们的群生成元，参与者 i 计算并 广播 每个多项式中的系数的 承诺 值 Cᵢ：

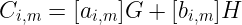
酷！现在剩下的就是 共享。为此，每个人需要 评估 他们的多项式。由于每个参与者都有一个索引 j，我们可以选择针对目标参与者在其索引处评估 共享，即 fᵢ(j)。

这意味着个人将从其他参与者 i 获取 fᵢ(j) 和 fᵢ’(j)。

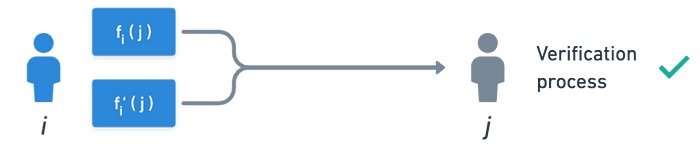
在收到这些值后，参与者 j 可以按如下方式 验证 它们：

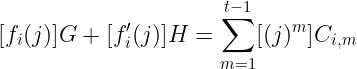
就这样！我们现在有了一种 可验证 的秘密信息共享机制。有了这个工具，我们可以开始构建我们的签名方案。

密钥生成

由于阈值签名涉及多个方，参与者将持有一个整数 dᵢ 作为其共享（或部分） 私钥。

然而，这并不是通常随机选择的整数。相反，参与者之间进行了 交互 的过程，最终生成他们的 私钥份额。这种协议称为 分布式密钥生成（DKG） 算法。

我们可以使用 VRSS 来构建我们的算法。多方便啊！

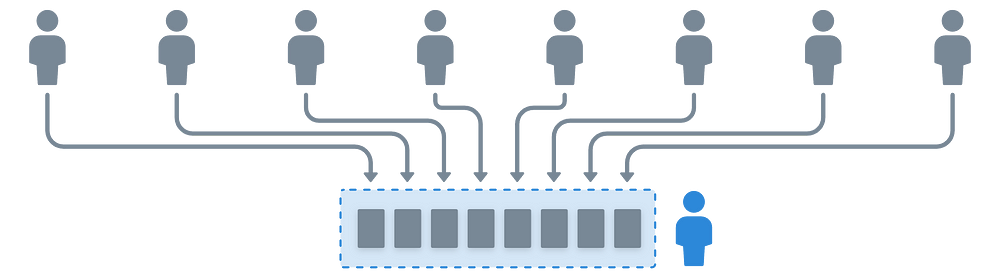
构建私钥的份额

每个参与者将从每个同行那里接收一个 份额，并利用这些 经过验证的 值来计算他们的 私钥份额：

可能有一些值未能通过验证；在这种情况下，有些参与方可能会被 取消资格。这就是为什么 VRSS 重要。

但为了使事情相对简单，我们将采用快乐路径。

DKG 的输出是一部分 共享私钥，d。参与此协议的各方对这个值 一无所知 — 仅知道它的 部分。

如果我们对私钥份额进行插值，我们会得到共享私钥。

最后，我们需要一个 公钥。为此，每个参与者广播他们的 秘密独立系数 或 零阶系数，aᵢ,₀。这个秘密不可公开，因此，它以 公开密钥份额 的形式传输：

我认为看到公开密钥份额的计算方式很奇怪。我敢打赌你预计会看到 dᵢ。

但其实有很好的理由不这样使用。我们稍后会回到该声明，因为我们需要定义一些内容，以理解实际上发生了什么。

一旦所有份额公开，所有参与者就可以独立计算全局公钥：

总结一下这个步骤：

密钥生成涉及各方之间的通信，生成共享私钥的片段。没有任何一个参与者知道共享私钥。与共享秘密相关的公钥也会被计算出来。

设置好所有密钥后，剩下的就是 签名。

签署消息

我们首先需要的是 要签署的消息。这并不简单，因为每个人需要 一致同意 一条消息。我们将不讨论如何实现这一点——让我们假设每个人都知道被签署消息 M。

在 ECDSA 中，签名者通常会选择一个随机的随机数 k，并相应地计算一个挑战 R = [k]G，生成如下的签名：

但正如我们已经看到的，这并不是 阈值密码学 通过怎么操作的。相反，一组 t 签名者将 相互通信 以生成签名。而他们首先需要的是一个 随机数。

幸运的是，我们已经有了一个生成分布式值的工具：DKG！我们就假设签名者执行一轮 DKG，获得一个份额 _kᵢ_和一个相关的挑战：

这些值会被广播，以便每个人都可以计算出一个共享挑战：

为了计算签名，大家都将使用 R 的 x 坐标，我们将其表示为 r。

构建签名

如你所猜测的那样，签名的生成也是 以份额形式 完成的。再次强调，只有在可用的份额满足一定数量时，我们才能通过这些独立计算的部分的 聚合 生成有效的签名。

我们的要求如下：签名份额 sᵢ 应该 插值 为最终签名 s — 在使用公钥 Q 时，该签名应通过验证。这里最自然的做法是调整 s 的表达式，使其使用构成部分的 份额：

但是这有意义吗？在这里，我们有 加法、乘法，甚至还有 模逆。假定它能就这样工作似乎不简单。

似乎很公正，我们应该检查这个表达式，确保它有效。实际上，它并没有你想象中的那么复杂。让我们慢慢来，一步一步。

相信我，这并没有那么糟糕！

插值加法

首先，让我们假设有两个多项式 a(x) 和 b(x)。如果我们在不同的值 i 上对他们进行评估，我们得到形式为 (i, a(i)) 和 (i,b(i)) 的点集。为方便起见，我们将它们分别记为 aᵢ 和 bᵢ：

我们知道，这些点的任何 t 个子集都可以插值回原始多项式。如果我们将 a(x) 的常数项定义为 a，我们可以写成：

作为提醒，在秘密共享的上下文中，我们通常对 常数项 感兴趣。这就是为什么当我们说插值一些值时，可能仅指输出为这个常数或零阶系数，而不是整个多项式。实际上，完整的输出是整个多项式！

类似地，假设 b(x) 具有常数项 b，那么我们可以写成：

如果我们 相加 多项式 a(x) 和 b(x) 会发生什么？

我们可以逐项相加，最终得到的多项式与原始多项式的度相同（ t - 1），但常数项为 g = a + b。同时，由于 g(x) = a(x) + b(x)，插值到 g 的所有点均为 (i, g(i))，可以计算为 aᵢ + bᵢ。因此：

这太棒了！这意味着我们基本上可以 添加多项式的份额，并在插值时得到 分享秘密的 总和。太棒了！

现在我们可以分析 公钥 计算。请记住，份额 dᵢ 被计算为 fⱼ(i) 值的总和。

正因如此，dᵢ 本质上是 多项式求和的份额，其常数项是所有 aᵢ,₀ 项的总和。所以，插值所有的 dᵢ 的结果将产生这个和！

所以，这就是为什么公钥的计算方式如此。这一切都是合理的！

插值乘法

乘法稍微复杂一些。当 a(x) 和 b(x) 相乘时，得到的多项式 h(x) 将具有 两倍的度。因此我们需要 两倍 的点数进行插值：

这并不是特别理想，因为现在我们需要更多的值来进行插值，这意味着各方之间需要更多的通信。

尽管有这个不便，好消息是它的行为如我们所期望的那样：当相乘 h(x) = a(x)b(x) 时，常数项 也被相乘，我们的值 aᵢbᵢ 也会插值为 h = ab！

同样值得一提的是：当份额乘以一个 常数 时，结果的插值也将被该常数乘以：

因此，如果我们将我们的份额取为 (i, k.aᵢ)，则插值将产生 k.a。挺简单吧？

布布兹先生对这事多少有些不高兴。

好的，我们只需分析最后一种情况。痛苦与折磨即将结束，我保证。

插值逆元

实际上，我们只需处理那个让人厌烦的模逆。我们想产生 kᵢ⁻¹ 的值，当插值时会产生 k⁻¹。这将需要几个步骤。好吧。

• 首先，所有人都将进行一轮 VRSS 以生成份额 αᵢ。当然，这些份额的插值如下：

• 然后，每个参与者将计算并广播：

• 由于 μᵢ 是 乘法 的结果，在接收 2t - 1 份额后，任何人都可以插值该值：

• 最后，每个参与者以如下方式计算 kᵢ⁻¹：

你问这巫术是如何工作的？嗯，考虑到这一点： μ⁻¹ 作为 常数项 向插值 kᵢ⁻¹ 的值插值。因为这样，我们得到了：

就像魔术一样，我们构造了插值到 k 的逆值的值！

现在你是一个巫师了，哈利。

我们需要的就这些！让我们回到我们的签名计算，看看我们刚刚获得的结论。

回到签名

如果我们可以重建每个共享秘密，那么签名计算将像标准 ECDSA 那样进行：

但是实际上，我们不想发生这种情况——我们只有 份额。因此我们问是否这个：

也插值为 s。答案是一个响亮的 是，因为我们只处理 加法、乘法 和 逆元素——我们已经知道它们的行为。

唯一的问题是，由于我们处理的是份额的 乘积（kᵢ⁻¹dᵢr 项），因此我们将需要 2 t - 1 的份额进行插值。但是抛开这个不谈，我们确信插值 sᵢ 的值将产生预期的值 s！

不同的协议可能采用各种技术来尝试减轻插值所需的额外点——理想情况下，我们希望将这个数字尽可能接近 t。此外，所需的通信步骤越少越好。

最后，当每个参与者计算他们的份额 sᵢ 时，他们只需进行广播。当足够的份额可用时，任何人都可以插值、生成并输出 s。

就是这样！简单吧？

我在开玩笑，这显然非常复杂。但总体的想法才是真正重要的结论：

在签名过程中，各方再次相互通信，生成共享签名的部分。当足够的部分可用时，最终签名可以被构建；如果部分不够，那么这就不可能。

验证 过程与往常一样，因为签名的输出只是对 (r, s) 的一对。

总结

我想这是我写过的技术含量最大的一篇文章。我尽力使其简单明了，但有些事情我们就不能回避地解释。至少，我希望这能在一些方面揭示一些从我经验来看，不通常详细解释的内容。

重要信息： 实际上，在我描述的过程中存在一个 相当大的漏洞，从分享 sᵢ 的过程中泄露了私钥份额。

这一问题在 我作为指导的论文 中有解决，而解决方法相当简单。因此，请不要根据这篇文章来构造你的阈值签名——或许可以参考实际的论文！

设计这种 多方计算 协议时，必须考虑恶意活动的存在。因此，通常这些协议充满了 资格淘汰轮次、正确性证明，甚至可能还有一些 加密 和其他有趣的内容。实际上，这是一系列不同技术的整合，往往相当复杂。

多方计算 通常是相当复杂的。

这是我能找到的最简单的方案，关于所需的工具，只是大致展示这些技术的主要组成部分。这意味着，积累的工具越多，构建更复杂方案的可能性就越大。

话虽如此，我们的旅程将继续，展示 又一个极其强大的工具，将解锁新的功能：配对。在 下一篇文章中 见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～