密码学基础：签名机制再解析

这是关于密码学的一系列文章中的一部分。如果这是你看到的第一篇文章，我强烈建议从系列的开始部分开始阅读。

如果你一直在关注这个系列，那么你已经见识了不少加密技术的花样。尤其是在上一篇文章中。不过……这仅仅是冰山一角。

但别担心。我们将缓慢而稳健地深入其中。

有许多内容等着我们去学习。我们可以使用椭圆曲线（以及一般的群体，公平地说）做很多事情。特别是，数字签名有一些优雅的变体，在特定的上下文中证明是非常有用的。这将是今天文章的主题。

友好的预警

我想在这个系列的这一点上，数学会变得稍微复杂些。待介绍的协议的复杂性略高。如果你只是想对加密技术有一个大致的了解，那么我建议你只阅读每个主题的介绍。我会尽我所能，把介绍保持简单和独立，从而提供一个良好的整体概念，不用为理解数学而烦恼。

让我们开始吧！

盲签名

在某些情况下，可能需要对私人信息进行签名。例如，在一个投票系统中，用户可能希望保持他们的投票私密，但需要某个第三方的认可。后者必须盲目签署投票——而不知道用户的投票是什么。

当然，即使这从技术上是可行的，盲签名也应该谨慎实施。毕竟你不想盲目签署一笔让你的银行账户清空的交易。

别着急

不过，如果需要盲签名，有很多方法来构造它们。一种可能性是适应现有的签名方案。特别是，适应 Schnorr 签名相对简单。让我们尝试一下！

关键是Alice不能知道她正在签署什么——她将被Bob要求签署某个他之前盲化或掩盖的消息M。而在制作签名后，Bob有办法将其解盲，从而对于他的原始消息能进行验证。

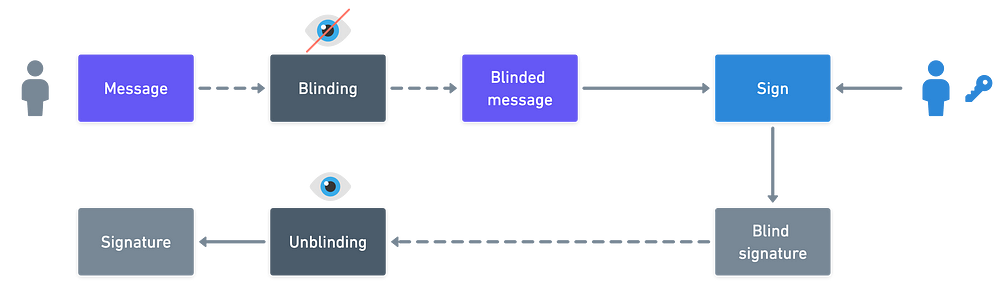
这一过程的简要视觉总结

简而言之：

盲签名允许对私人信息进行签名。

协议

我们像往常一样开始：Alice拥有私钥d和公钥Q = [d]G。她将作为我们的签名者。和往常一样，G是所选椭圆曲线群的发生器，并且有顺序n。

此过程始于Alice选择一个随机整数k，并计算R = [k]G。她将此发送给Bob，然后他开始盲化过程：

• Bob选择一个称为盲化因子的随机整数b，
• 然后他计算：

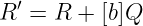
• 然后用此计算一个挑战：

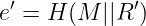
• 最后，他也盲化这个挑战：

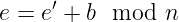
剩下的就是让Alice签署。她接收e，并简单地按常规计算签名：

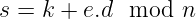
在这一特定示例中，Bob在收到签名时不需要做任何事情——输出就是(s, e')。但通常情况下，他可能需要在其他版本的盲签名中逆转盲化过程。

验证过程与标准的 Schnorr 签名情况完全相同：

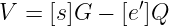
如果这恰好等于R'，那么H(M | V)将恰好等于挑战e'，签名将被接受。这应该是这样，因为：

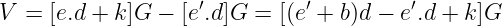
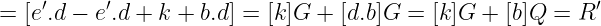
像时钟一样，我们看到正确计算的s实际上应该验证签名（因为我们得到了原始挑战）。

顺便提一下，我故意省略了模 n运算，以简化说明。但对于严格处理，应该将其纳入演示中。

盲签名，确认。没那么疯狂，对吧？

现在我们已经热身，让我们提升一下难度……

环签名

每次你数字签署某个东西时，验证时都需要知道你的公钥。因此，你没有匿名性：你的公钥标识了你是持有私钥的个体。但如果我告诉你，有一种方法可以实现匿名签名呢？

环签名提供了这样的功能。前提是，来自一组人的单个实体生成的签名不揭示出哪一个人在组内是原始签署者。像这样：

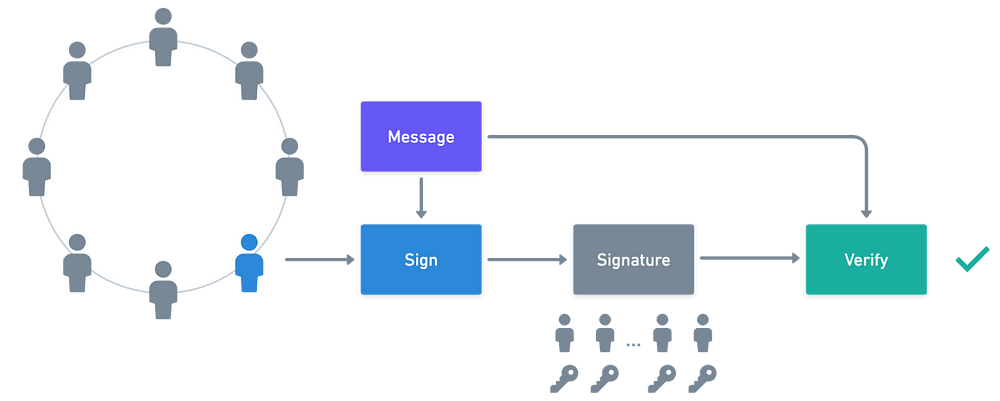
（等我们解释完时，这会更容易理解，我保证）

再次简要概述：

环签名允许组中的用户创建一个签名，该签名可以由组的任何成员生成，从而保护用户的匿名性。

创建环

为了实现这种匿名性行为，我们必须首先伪造一种新且稍微不寻常的结构，称为环。

不是那个戒指，弗罗多！

环的概念是一种有序的参与者集合，其顺序决定了一系列计算，从一个值A开始，并以同样的值A而结束。和往常一样，构建该计算序列只有在知道私钥的情况下才可行。

顺便提一下，这不是指抽象代数结构中的环。我们稍后会谈论那些。

因此，设置如下：环有p个参与者，正如前面提到的，它们是有序的。也就是说，Alice是第一个参与者，Bob是第二个参与者，依此类推。

莎拉，作为第s个参与者，了解所有其他参与者的公钥——我们将记作Qᵢ。她还拥有自己的私钥和公钥对，即dₛ和Qₛ = [dₛ]G。

为了为一条消息M生成签名，莎拉执行以下操作：

• 她选择一个随机整数k，并计算R = [k]G。
• 然后，她计算一个种子，v = H(M | R)。

这个种子将用于一个迭代过程。她首先将eₛ设置为v，然后对于环中的每个其他参与者p：

• 她选择一个随机值kᵢ，并计算：

• 并计算下一个挑战：

最终，莎拉这样处理所有参与者，得到最终的挑战，我们将其称为e。她按照顺序，从第s + 1个参与者开始，到达第p个参与者后，再从1计数到s - 1。这至关重要，因为签名将在同样的顺序中被评估。

剩下的就是她关闭环，意味着最终计算应该回到初始值eₛ = v。为此，她必须找到某个值kₛ₋₁使得：

我们知道eₛ等于H(M | R)——我们的方法值——所以实际上，我们需要找到一个值kₛ₋₁使得R = Rₛ₋₁。稍微调整一下：

我们可以得到期望的kₛ₋₁。最后的签名是元组：

重要的是，值必须按环顺序提供。莎拉会藏在其中……

这里有搓全签名过程的视觉表述，以帮助更好地理解参与的所有步骤：

验证

剩下的就是验证签名。为此，Bob从e₁开始，为每个参与者i计算以下内容：

• 值Rᵢ = [kᵢ]G + [eᵢ]Qᵢ
• 然后计算下一个挑战：

如果循环正确闭合，意味着最终挑战恰好为e₁，那么他就接受签名。注意环能够闭合是因为我们确保为莎拉找到了适合的kₛ₋₁！而我们是用莎拉的私钥做的——如果我们不知道它，那么找到正确的kₛ₋₁就不是一件轻松的事。

从验证者的角度来看，所有的k值是不可区分的（它们只是一些数字），因此他无法知道哪个是计算出的——记住，其他的只是随机的！

好的，这确实是很多内容！

警告：接下来是求和。喘口气。喝水。暂停一下。

准备好了吗？让我们继续。

多签名

这个想法很简单：如果我们要求多个参与者签署某个东西呢？这并不是不切实际的：在签署现实世界的法律文件时，这通常是一个要求。这感觉如同一个非常自然的拓展。

多签名在签署敏感操作时特别有用。例如，在一个应用中，管理员操作可能需要多个成员的签名。这确保没有单个行为者拥有管理员权限，也不存在单一的失败点。

遵循前面示例的模式，让我们在跳入数学之前对其进行简要总结：

多签名允许多个用户对单条消息签名，因此如果没有足够用户签名，则签名无效。

这有多种方式来实现。

Schnorr 多签名

Schnorr 签名有一个非常好的属性：它们是线性的。简单来说，这意味着我们可以将单个签名相加，依然能得到一个有效的签名。这里没有复杂的乘法逆元素，这可能会给事情带来复杂性。

因此，我们可以适应我们已经呈现的方案，使得多个参与者可以对一条消息进行签名。

设置与通常的略有不同：每个p的参与者都持有一个私钥dᵢ，并且有一个公钥Qᵢ = [dᵢ]G。我们还需要一个组合公钥**Q**，计算如下：

请注意，这与我们如果首先将私钥相加再计算Q时获得的结果完全相同：

之后，签名的过程如下：

• 每个参与者选择一个随机数kᵢ，并计算Rᵢ = [kᵢ]G。
• 然后，个体的Rᵢ被组合如下：

• 用此，计算挑战e，为e = H(R | M)。
• 然后，每个参与者计算单个签名sᵢ：

• 最后，将部分签名相加以产生一个单一的s，为：

和之前一样，产生的签名是对（e, s）。有趣的是，这对的验证完全像一个普通的 Schnorr 签名！验证者计算R’ = [s]G + [e]Q，并接受如果e = H(R’ | M)。在这里，线性性便发挥了作用：我们可以展示R’应该等于R**，因此签名应该有效。

请记住，我故意省略了模 n运算，以保持简单和干净。严格处理要求你考虑该操作！

这样一来，多个参与者就生成了一份合署名！真不错！

阈值签名

阈值签名提供了一种稍微高级的功能。术语阈值暗示了在签名有效之前，必须有一定的最少签名者参与。我们要求从一组m人中选择t个参与者进行签名，以生成签名。

一如既往，我们需要私钥。但和之前一样，关键点是没有单个行为者知道它——他们只持有份额或部分。在阈值签名事件中实现这一点并不是轻而易举的——不能简单地选择一个随机整数。

阈值密码学并不是简单的事情

事实上，密钥生成是阈值签名能够正常工作的关键步骤。

如实地说，理解阈值签名需要使用多项式，而我们尚未涵盖这些。它们将成为未来文章的中心话题。现在，我们只能满足于知道这种类型签名的存在。我们稍后会在系列中再讲。

总结

签名有很多不同的形式。归根结底，这都是在创造一种具有某些特定特性的加密游戏。无论你有什么需求，你大概能想出一种覆盖它的策略。

你需要匿名签名，但有一个可以撤销签名的管理员吗？群签名可以来拯救你。想修改消息但保持有效签名？同态签名就是你的选择。

我们现在已经看到基于群体的相当数量的密码学应用。现在是时候加深对群体的进一步理解——所以下一次，我们将研究群体同态性和同构性。而且进一步讨论一种新的有用的密码学技术。

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～