掌握SP1 zkVM设计 - 第3部分:核心证明
- gavin.ygy
- 发布于 2025-02-20 16:29
- 阅读 2942
本文详细介绍了SP1 zkVM设计中的核心证明部分,包括多项式承诺方案(PCS)、Fiat-Shamir挑战生成器、FRI协议、低度扩展(LDE)和开放证明。文章深入探讨了这些技术的实现细节和数学原理,旨在构建高效的零知识证明系统。
1. PCS (多项式承诺方案)
在零知识证明系统中,多项式承诺方案 (Polynomial Commitment Scheme, PCS) 是一种密码学原语,它允许证明者将多项式“绑定”到一个短的承诺值,并有效地证明该多项式在特定点上满足某些性质(例如,低度和正确性)。它是构建高效 STARK/SNARK 系统的核心组件。
Plonky3 的基础承诺方案是 混合矩阵承诺方案 (Mixed Matrix Commitment Scheme, MMCS),这是对向量承诺方案的一个推广,支持承诺矩阵和行开放。相关代码位于:
p3/commit/src/mmcs.rs定义 MMCS APIs。p3/commit/src/domain.rs定义 MMCS 使用的多项式空间(域),这是一个 2-进制乘性余类 (2-adic multiplicative coset)。merkle-tree/src/mmcs.rs是 MMCS 的具体实现 (FieldMerkleTreeMmcs)。
SP1 直接使用 Plonky3 的高级基于 FRI 的多项式承诺实现,位于 p3/fri/src/two_adic_pcs.rs。关键 APIs 包括:
1.1 commit
此函数是 PCS 的核心,为多项式生成承诺。对于 SP1,它在输入的 domains 和 traces 上使用 Radix2DitParallel 执行 COSET LDE(见第 4 节:LDE)。然后,使用底层的 FieldMerkleTreeMmcs 为 LDE 扩展的矩阵计算 Merkle 承诺,返回 commitment(Merkle 根)和 prover_data(Merkle 叶子,即 LDE 扩展的矩阵)。
1.2 open
此函数生成一个 开放证明,允许证明者展示在特定点上多项式评估的正确性,而不暴露整个多项式。详细信息见第 5 节:开放证明。
1.3 verify
此函数验证开放证明,确保所指定点的多项式评估的正确性,并确认其低度属性。
1.4 natural_domain_for_degree
给定一个多项式度数 n,此函数返回一个用于多项式插值和评估的评估域(一个 2-进制乘性余类)。
1.5 get_evaluations_on_domain
此函数从 prover_data 中检索索引为 idx 的 LDE 扩展矩阵(一个特定的 Merkle 叶子),基于域大小提取其前半部分,应用 bit_reverse_rows 以匹配目标域的顺序,并返回结果。
2. 挑战者
Fiat-Shamir 是一种将互动证明系统 (IOPs) 转换为非互动证明的技术,通过使用哈希函数来模拟验证者的挑战。SP1 使用 DuplexChallenger 位于 p3/challenger/src/duplex_challenger.rs,它利用 Duplex Sponge 结构和密码学置换进行安全和高效的挑战生成。关键 APIs:
2.1 observe
将数据(域元素、数组、哈希值等)吸收至 input_buffer。当缓冲区达到其容量( RATE)时,一个双重运算会更新内部状态。SP1 使用此方法吸收承诺值。
2.2 sample
从 output_buffer 中提取随机挑战。如果 output_buffer 为空或 input_buffer 非空,首先触发双重运算。
2.3 duplexing
从 input_buffer 吸收数据到海绵状态,应用置换,更新状态,并填充 output_buffer。
2.4 sample_ext_element
通过以下方式生成随机扩展域元素:
(1) 采样多个基本域元素。
(2) 将它们组合成一个扩展域元素。
3. FRI
Plonky3 的 TwoAdicFriPcs 在其 open() 函数中调用 prover::prove 以生成 FRI 证明。SP1 直接使用此逻辑。
3.1 FRI 协议概述
FRI 通过迭代折叠来降低多项式的度数,然后进行低度验证。分为两个阶段:
- 承诺阶段:证明者迭代折叠多项式并对每一层进行承诺。
- 查询阶段:验证者随机选择位置,证明者提供所有层的开放证明。
3.2 折叠 (fold_even_odd)
任何多项式都可以分为偶数项和奇数项。

折叠通过随机挑战 β 将它们结合起来:

3.3 低度测试
FRI 在每一轮中将多项式的度数从 d 降低到 d/2^k,最终验证它是否变为常量。随机挑战 β 确保证明者的诚实。
4. LDE (低度扩展)
LDE(低度扩展)编码函数被称为系统函数,其中输入向量 a(即消息)是其编码 LDE(a) 的一个子集。与 Reed-Solomon 编码相比,低度扩展编码的系统特性使其具有良好的结构形式,使得证明者和验证者能够以特别高的效率进行操作,在互动证明和论证的背景下更具实用性。
在 SP1 中初始化 FRI 时,LDE 被指定使用来自 p3/dft/src/radix_2_dit_parallel.rs 的 Radix2DitParallel。虽然 SP1 不直接调用与 Radix2DitParallel 相关的函数,但这一部分与 PCS(多项式承诺方案)密切相关。
radix_2_dit_parallel 是一种并行 FFT 算法,将蝴蝶网络的层分成两半。对于第一半,我们在早期层中应用较小块的蝴蝶网络,即 DIT 或 Bowers G。然后我们进行位反转,对于第二半,我们继续按位反转的顺序执行相同的网络。这样,我们始终处理小块,因此在每一半中,我们可以在不进行跨线程通信的情况下拥有一定的并行性。关键 APIs:
4.1 dft_batch
此方法对 RowMajorMatrix 的每一列执行离散傅里叶变换(DFT),采用分治策略。FFT 被分为两个阶段:第一半使用标准递归 DIT(时间上的分解),第二半继续按位反转的顺序处理,然后返回结果矩阵。
4.2 coset_lde_batch
此方法将 RowMajorMatrix 插值到更大的余类(即,余类低度扩展),允许对该余类的子集进行评估。在 SP1 的初始化( sp1/stark/src/config.rs)中,指定 DFT 应使用 Radix2DitParallel,因此在调用 p3 的 commit 时,使用 coset_lde_batch() 函数。完成后,结果矩阵的高度增加,而宽度保持不变。这个高度与 log_blowup 相关。在 SP1 中,log_blowup=1,因此结果矩阵的高度是原来的两倍(1 << log_blowup)。
5. 开放证明
p3/fri/src/two_adic_pcs.rs 中的开放函数可以批量开放多个多项式并生成开放证明。它利用 FRI 协议证明在多个点上的开放值的一致性及相应多项式的低度属性,确保已承诺的多项式满足期望的约束。
5.1 复合多项式
开放函数中的一个关键步骤是将多个多项式的开放值转换为单个多项式的开放值,即计算:

其中:
- q(x) 是复合多项式的商多项式;
- α 是一个随机挑战值;
- pᵢ(x) 是目标多项式;
- zᵢ 是开放点;
- yᵢ 是多项式 pᵢ 在点 zᵢ 的开放值,使用重心插值法计算;
- x, pᵢ(x) 在基本域中,而 α, zᵢ, yᵢ 在扩展域中。
5.2 原理
如果开放值是正确的,则多项式 pᵢ(x) − yᵢ 在 x = zᵢ 处有一个根。因此,商多项式 q(x) 是一个低度多项式,可以使用 FRI 验证其低度属性。
5.3 重心插值
在有限域上的重心插值公式如下:
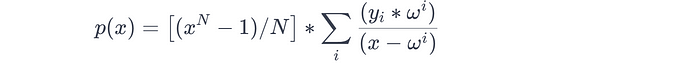
其中:
- ω 是 N 次乘法子群的生成元,满足 ω^N = 1 且 N 是 2 的幂;
- yᵢ 是多项式 p(x) 在 xᵢ 处的评估。
更多详细信息见:快速重心评估教程 — HackMD。
在 Plonky3 实现中,上述算法略有修改。函数代码如下:
/// 给定在给定的标准的 N 次幂的余类上批量多项式的评估,计算多项式在 `point` 的值。
pub fn interpolate_coset<F, EF, Mat>(coset_evals: &Mat, shift: F, point: EF) -> Vec<EF>
where
F: TwoAdicField,
EF: ExtensionField<F> + TwoAdicField,
Mat: Matrix<F>,
{
// 此方法的轻微变体: https://hackmd.io/@vbuterin/barycentric_evaluation
let height = coset_evals.height();
let log_height = log2_strict_usize(height);
let g = F::two_adic_generator(log_height);
let diffs: Vec<EF> = cyclic_subgroup_coset_known_order(g, shift, height)
.map(|subgroup_i| point - subgroup_i) //x-x_0, x-x_1, x-x_2,...
.collect();
let diff_invs = batch_multiplicative_inverse(&diffs);
// TODO: 加快此速度
let col_scale: Vec<_> = g
.powers()
.zip(diff_invs)
.map(|(sg, diff_inv)| diff_inv * sg) //=权重:w_i
.collect();
let sum = coset_evals.columnwise_dot_product(&col_scale);
let zerofier = two_adic_coset_zerofier::<EF>(log_height, EF::from_base(shift), point);
let denominator = F::from_canonical_usize(height) * shift.exp_u64(height as u64 - 1);
scale_vec(zerofier * denominator.inverse(), sum)
}5.4 证明
FRI 协议在 p3/fri/src/prover.rs 中实现。prove() 函数生成 FRI 证明。commit_phase() 函数实现 FRI 的承诺阶段,在此期间调用折叠函数 fold_even_odd()。answer_query 函数实现 FRI 的查询阶段。
6. 参考文献
1) SP1 技术白皮书, https://drive.google.com/file/d/1aTCELr2b2Kc1NS-wZ0YYLKdw1Y2HcLTr/view
2) https://learnblockchain.cn/article/19265/
3) Ulrich Haböck 和 Al Kindi。关于在 STARKs 中添加零知识的注释。2024 年 4 月,https://eprint.iacr.org/2024/1037.pdf
4) Starkware101. https://starkware.co/wp-content/uploads/2021/12/STARK101-Part2.pdf
5) Ulrich Haböck。关于 FRI 低度测试的总结。IACR ePrint Archive 2022/1216, 2022. https://eprint.iacr.org/2022/1216。
6) Coset. https://github.com/coset-io/zkp-academy/tree/main/FRI%26Stark
7) Trapdoor-Tech. https://trapdoortech.medium.com/zero-knowledge-proof-introduction-to-sp1-zkvm-source-code-d26f88f90ce4
8) StarkWare 团队。ethSTARK 文档 — 第 1.2 版。在 IACR 预印本档案 2021/582, 2023. https://eprint.iacr.org/2021/582。
9) Plonky2. https://github.com/0xPolygonZero/plonky2。
10) Plonky3. https://github.com/Plonky3/Plonky3
11) Succinct labs. https://github.com/succinctlabs/sp1
12) Justin Thaler. 证明、论证与零知识。2022 年 12 月。
13) Vbuterin. 快速重心评估教程。https://hackmd.io/@vbuterin/barycentric_evaluation
- 原文链接: medium.com/@gavin.ygy/ma...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,在这里修改,还请包涵~
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 50 浏览
- 零知识编年史:群 29 浏览
- 以太坊执行层优化:状态树与虚拟机 160 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 163 浏览
- 首次 ZK 攻击发生,且出乎意料 189 浏览
- Vitalik: 以太坊量子抵抗路线图 138 浏览
- zkMesh:2026年2月回顾 178 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 144 浏览
- 量子可恢复的 Zcash 157 浏览
- ZK编年史:哈希登场 242 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 441 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 364 浏览

