ECDSA、EdDSA 和 Schnorr——基于椭圆曲线的签名方案剖析
- barchitect
- 发布于 2024-10-20 11:15
- 阅读 30
本文详细介绍了基于椭圆曲线的数字签名方案，包括ECDSA、EdDSA和Schnorr，分析了它们的原理、实现和应用，并比较了它们在区块链中的使用情况。
ECDSA、EdDSA 和 Schnorr——基于椭圆曲线的签名方案分析
ECDSA、EdDSA、Schnorr——基于椭圆曲线的签名方案分析。
数字签名方案（或算法，DSA）可能是密码学和区块链中最重要的协议。它们是所有区块链的安全基础，美妙地构建了许多先进的密码协议，如多方计算（MPC）、可验证随机函数（VRF）和零知识证明（ZKP）。我认为，数字签名方案可以根据其基础的密码学基础进行分类，如基于椭圆曲线和基于配对的方案。在本文中，我旨在详细说明第一类：基于椭圆曲线的签名方案，如ECDSA、EdDSA和Schnorr。这些算法在区块链中都是重要的。ECDSA是以太坊使用的签名方案，EdDSA被Solana和TON区块链采用，而Schnorr方案最近被纳入比特币协议，在Taproot升级中实现。让我们开始吧！
数字签名方案分类
在处理DSA时，你可能会注意到它们都有着相似的密码基础。例如，流行的ECDSA、EdDSA和Schnorr方案都基于椭圆曲线密码学，它们的安全性依赖于离散对数问题（DLP） [2] 的困难性。另一方面，最近的BLS签名方案依赖于基于配对的密码学 [1]，它们的安全性依赖于双线性映射 [1]，与DLP是不同的数学基础。这种密码学数学的差异也导致了不同的属性，例如BLS方案的签名聚合能力。
因此，我们可以根据其密码学基础对DSA进行分类，例如基于椭圆曲线的签名方案和基于配对的签名方案。第一类包括许多在区块链中流行的方案，例如ECDSA、EdDSA、Schnorr。这些方案在基础椭圆曲线和协议设计方面彼此不同。此外，与这些方案相关联的安全假设也各不相同。我们将逐一探讨每个方案，首先从ECDSA开始。
ECDSA 签名方案
椭圆曲线数字签名算法（ECDSA）是一个标准，用于生成任意消息的数字签名。这样的数字签名可以由第三方以非交互的方式进行验证。
该协议可以分为两个阶段：签名生成和验证。让我们看看它是如何工作的！
签名生成
想象一下，Alice想要为消息m创建ECDSA签名，然后该签名由Bob进行验证。假设Alice和Bob提前达成一致，他们将使用有限域F_q上的某个标准椭圆曲线E [1]，并有一个生成元G。除非另有说明，所有计算都是modulo q进行的。
首先一步，Alice通过从F_q中随机抽样生成她的私钥a。完成后，她通过将其私钥a与生成元G相乘，推导出公钥A。
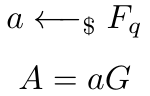
然后，Alice从F_q中随机抽取另一个值k，称为“nonce”（一次性使用的数字）。确保这个值是完全随机且从不重用是极其重要的。ECDSA的安全假设确实在很大程度上依赖于这一步。我们稍后将深入探讨这个安全影响。
接下来，通过将k与生成元G相乘来得出值R。
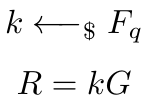
由于值R是椭圆曲线E上的一个点，它具有x和y坐标。因此，Alice可以将值r定义为R的x坐标。
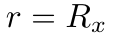
如果r=0，Alice需要丢弃k并随机抽取另一个nonce k，并像之前一样得出R和r。必须一直进行此操作，直到r≠0。
现在，Alice需要将她想要签名的消息m转化为可以“映射到”椭圆曲线E上的表示。这可以通过通过加密安全性哈希函数 H（例如SHA-256）对m进行哈希处理来完成。消息的哈希值被截断，以使哈希的位数与有限阶q的位数相同。截断后的哈希是一个整数，记为z。
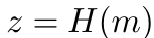
最后她计算出值s。
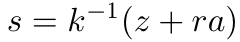
如果s=0，Alice需要丢弃k并随机抽取另一个nonce k，并像之前那样得出R、r和s。必须一直进行此操作，直到s≠0。
消息m的签名是元组(r, s)，Alice可以将其与她的公钥A一起发送给Bob进行验证。你可能会注意到在以太坊中，签名确实是(v, r, s)而不是(r, s)。这是由于以太坊中的一个故意设计选择，以支持高效的公钥恢复。我们稍后将深入探讨。
签名验证
要验证Alice的签名，Bob按照以下步骤重新计算z。
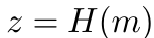
接着，他计算u、v和R如下。
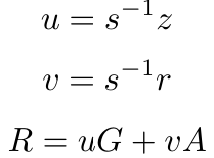
如果r等于R_x（R在椭圆曲线E上的x坐标），则签名是有效的。该协议如下图所示。
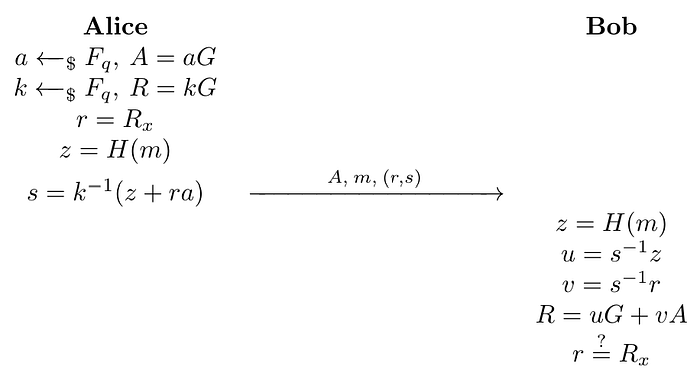
ECDSA签名方案。
它为什么有效
ECDSA签名方案的正确性证明如下。首先我们查看R并对其进行展开，得到。
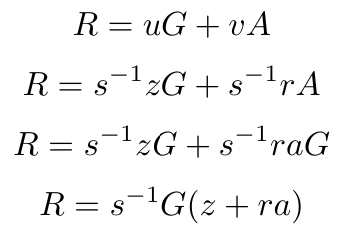
回忆一下。
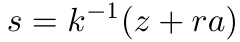
将s代入上述方程中，我们得到。
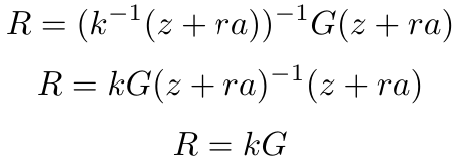
这意味着Bob在他一侧计算的椭圆曲线点R等于Alice在她一侧计算的点R。如果签名有效，r等于R_x，即点R的x坐标，反之亦然。因此，协议的正确性得到了证明。
以下是ECDSA签名方案的代码示例。
曲线选择
ECDSA签名方案中采用的椭圆曲线是secp256k1。这条椭圆曲线是Weierstrass曲线之一，我在我先前的文章“高级密码学原语” [1] 中进行了回顾。
安全级别
ECDSA的安全级别为128位，这意味着理论上需要2¹²⁸次操作来对签名系统进行暴力攻击。具体来说，这将涉及尝试通过在有限域F_q中尝试所有可能元素来推导私钥。然而，这种攻击在实践中是不可行的，128位的安全级别被认为在当前计算能力下是安全的。
以太坊签名
ECDSA确实是以太坊的签名方案。然而，你可能会注意到，以太坊中的签名表示为(v, r, s)而不是我们之前讨论的(r, s)。以太坊签名中额外的参数v是一个故意的设计选择，用于足够的公钥恢复。让我们深入探讨一下。
v的目的
- 公钥恢复：以太坊使用一种称为“公钥恢复”的技术，从签名和消息哈希中导出公钥。这是有用的，因为它允许区块链在不需要显式存储公钥的情况下验证交易的来源。
- 椭圆曲线点的不明确性：从ECDSA签名中恢复公钥时会存在不明确性，因为对于给定的
x坐标，椭圆曲线点可能存在两个可能的y坐标。值v有助于解决这种不明确性，通过指示应使用哪个两个可能的y坐标来进行计算。下图说明了这一点。
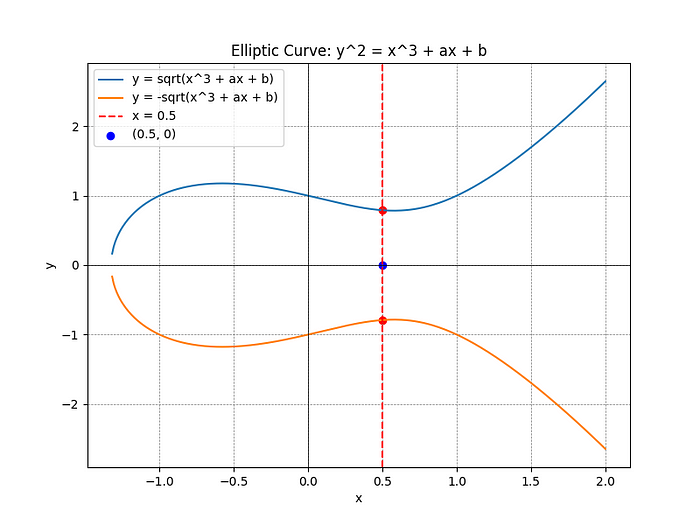
对于给定的x坐标，在椭圆曲线E上存在两个y坐标。
v是如何工作的
- v的值：在以太坊中，v通常为27或28。这些值源于恢复过程，指示应使用用于重建公钥的两个可能解中哪个
y坐标应当使用。 - 签名验证：在验证过程中，以太坊使用
(v, r, s)值恢复公钥，并验证其是否与发送者的地址匹配。这是通过ecrecover函数完成的，该函数是以太坊虚拟机（EVM）的一部分。
对nonce的攻击向量
请回忆，在签名生成阶段，Alice必须生成一个nonce k。确保nonce是不可预测的且不重复使用至关重要。否则，Alice的私钥可能会被泄露。我们来看一下原因。
假设有两个具有相同nonce k的签名，如(r1, s1)和(r2, s2)。回忆一下，r等于点R=kG的x坐标，我们有r1=r2，因为两个签名共享相同的点R。
从已知值r、s1、s2中，我们可以提取k，如下所示。
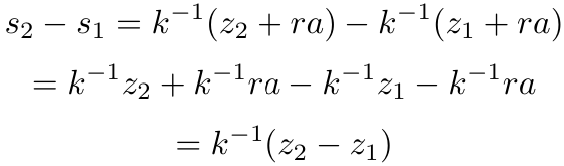
即。
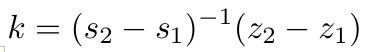
使用计算出的k，我们可以从任何消息m的签名(r, s)推出私钥a，即z=H(m)，方法如下。
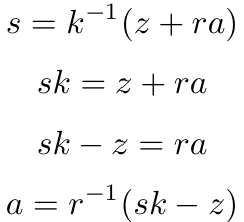
nonce的生成步骤将在ECDSA签名方案上引入攻击向量。强大且安全的nonce生成程序对于任何ECDSA实现至关重要。这一弱点导致了一种不需要nonce生成步骤的更安全的签名方案，EdDSA签名方案。让我们下一个探讨。
EdDSA 签名方案
EdDSA是在ECDSA之后引入的一种数字签名方案，旨在快速且安全。它基于椭圆曲线密码学，并使用扭曲的爱德华曲线。EdDSA以其高效性和安全性而闻名。Ed25519是对Curve25519椭圆曲线的EdDSA的一种具体实现。为了明确起见，在本节中，我们将回顾Ed25519方案。
值得注意的是，EdDSA与ECDSA之间存在稍微不同的密码学基础。该协议使用扭曲的爱德华曲线，而不是ECDSA中使用的Weierstrass曲线。
扭曲的爱德华曲线
回想一下，椭圆曲线是满足方程[1]的点P(x, y)的集合：
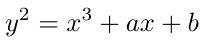
其中a、b是整数。这种经典形式的椭圆曲线称为Weierstrass形式。以Weierstrass形式表示的曲线也称为Montgomery曲线。
虽然许多椭圆曲线是以Weierstrass形式表示的，例如ECDSA使用的secp256k1，还有一些曲线可以用Weierstrass形式或一种称为“扭曲的爱德华形式”的新形式表示，如下所示。
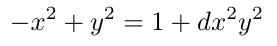
其中d是定义椭圆曲线的有限域F_q的元素。
扭曲的爱德华形式允许更有效的算术操作，特别是在加密协议中常见的点加法和点翻倍。这种高效性是Ed25519签名方案使用扭曲的爱德华形式的Curve25519的关键原因。扭曲的爱德华形式的Curve25519表示如下。
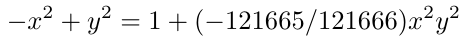
即d = -121665/121666。你可能会注意到d是一个有理数，而不是有限域中的整数。实际上，d的有理数形式是用于理论描述的简化。在实践中，d的实际值是通过分子与分母的模逆相乘得出的。
实际值为：
d=37095705934669439343138083508754565189542113879843219016388785533085940283555
以下是确定d的代码。
Curve25519
Curve25519是一种友好的扭曲的爱德华形式的椭圆曲线。它可以用Weierstrass形式或扭曲的爱德华形式表示。Curve25519在Weierstrass形式中的方程为：
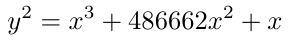
然而，Curve25519通常以扭曲的爱德华形式表示，以提高加密算术操作的效率，例如加法和翻倍。不妨提醒一下，Curve25519的扭曲爱德华形式如下。
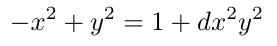
其中d= (— 121655/121666)
Curve25519在一个素数q=2²⁵⁵-19的有限域F_q上定义；q是平衡场的阶 [1]。该曲线的生成元 G(x, y) [1]的y坐标等于4/5，而x坐标的计算如下。
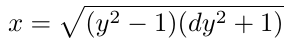
与d类似，生成元G(x, y)的有理形式y=4/5是用于理论描述的。实际上，x和y坐标都是有限域F_q的元素。在实践中，y的实际值通过将分母的模逆相乘计算得出。
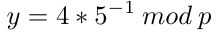
生成元G(x, 4/5)的实际坐标为：
x=1
y=46316835694926478169428394003475163141307993866256225615783033603165251855960
以下是确定这些坐标的代码。
该生成器G的阶 [1]为n， n=2²⁵²+27742317777372353535851937790883648493。Ed25519中的所有运算都是modulo n进行的，除非另有说明。
因此，椭圆曲线的余因子 [1] h=q/n等于8。
与ECDSA类似，我们将探讨签名算法的两个阶段：签名生成和验证。
签名生成
想象一下，Alice想为一个消息m创建Ed25519数字签名，然后由Bob进行验证。作为第一步，Alice需要生成她的私钥a。
EdDSA生成私钥的过程比ECDSA更复杂。EdDSA引入了一个新参数b，以及在签名过程中使用的输出为2b - 个比特的哈希函数H。b的一个重要属性是有限域F_q中所有元素都可以使用(b-1)位编码。具体来说，在Ed25519中，b=256，而哈希函数为SHA-512。容易证明，所有有限域F_q中的元素；q=2²⁵⁵-19都是可以使用255位编码的。
私钥生成始于256位随机种子，记为s，这个随机种子是签名系统的私钥。s的SHA-512哈希值H(s) = (h_0, h_1, h_2, …, h_511)决定一个整数如下。
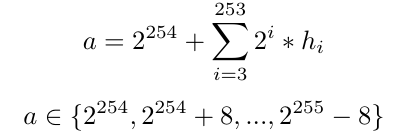
整数a称为秘密标量（secret scalar）。
将a乘以生成元G，我们得到曲线上的一个点A=aG，其x坐标A_x就是Ed25519的公钥。
在私钥s下，消息m的签名定义如下。一个随机值r通过将H(s)的后256位哈希{h_256, h_257, …, h_511}与消息m进行哈希获得：
这进而确定椭圆曲线点R=rG。接下来我们定义：
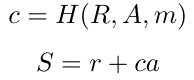
其中c是对R、A和消息m的哈希函数的输出；n是生成器G的阶。
(R, S)是在私钥s下消息m的签名。Alice将此签名、她的公钥A、消息m发送给Bob以进行验证。
签名验证
验证签名的过程如下。
作为第一步，Bob重新计算哈希值c=H(R, A, m)。
然后，他验证如下方程是否成立。
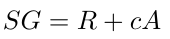
如果方程成立，签名(R, S)是有效的。该协议如图所示。
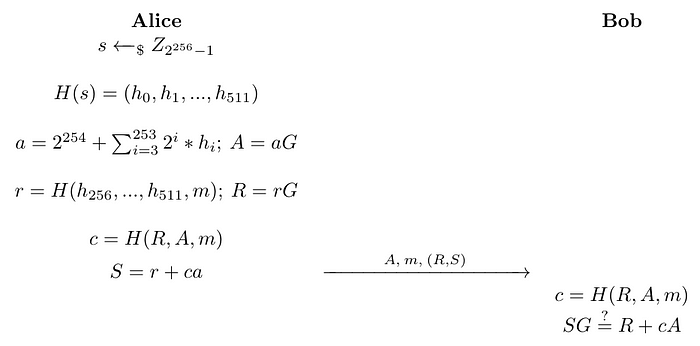
它为什么有效
假设Alice是诚实的，我们有S=r+ca；将该方程两边都乘以生成元G，我们得到。
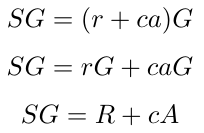
即如果最后的方程成立，则签名有效。安全性正确性得到证明。
安全级别
Ed25519签名方案与ECDSA的安全级别均为128位。
代码示例
以下是Ed25519签名方案的代码示例。
Schnorr 签名方案
本文中我们审查的最后一个签名方案是Schnorr签名方案。令人惊讶的是，它于1989年引入，早于ECDSA（1992年）和EdDSA（2011年）。尽管经过了充分研究并应用于先进的密码学，Schnorr签名方案最近才在区块链空间中引起了关注。它在2021年被纳入了比特币协议的Taproot升级中。
Schnorr签名方案以其简单性和效率而闻名。与ECDSA和EdDSA一样，它的安全性依赖于离散对数问题（DLP）的困难性。与其他方案不同，Schnorr方案是曲线无关的，这意味着它可以使用任何适合的椭圆曲线实现，无论是Weierstrass还是扭曲的爱德华。在比特币中，Schnorr签名方案是基于secp256k1曲线实现的。Schnorr方案在区块链中的应用也由于其支持高级密码技术的能力，例如多方签名计算，我们稍后将探讨。
让我们探讨签名过程的两个阶段：签名生成和验证。
签名生成
想象一下，Alice希望为一条消息m创建Schnorr数字签名，然后由Bob进行验证。假设Alice和Bob提前达成一致，使用有限域F_q中的椭圆曲线E，其中q是一个大素数。Schnorr方案中所有操作均在modulo q下进行，除非另有说明。椭圆曲线E具有生成元点G。
首先，Alice需要从F_q中抽取一个随机值来生成私钥a。完成之后，她通过将私钥a与生成元G相乘，推导出公钥A。
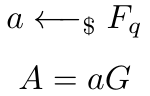
与ECDSA相似，在获得私钥和公钥后，Alice从有限域F_q中获取一个随机“nonce” k。将k与生成元G相乘，我们得到一个点R。
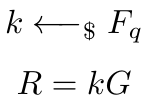
接着，通过将G、A、R和消息m哈希来确定值c，哈希函数如SHA-256。
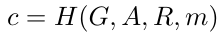
使用r、c、k来确定值e，使得。
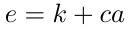
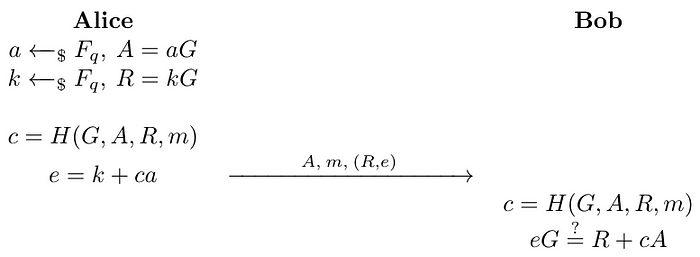
在私钥a下消息m的签名为(R, e)。Alice将这一签名与她的公钥A和消息m一同发送给Bob进行验证。
签名验证
为了验证签名(R, e)，Bob首先重新计算哈希值c，如下所示。
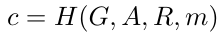
然后，他验证以下方程是否成立。
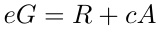
如果方程成立，签名有效。该协议如下图所示。
它为什么有效
假设Alice是诚实的，我们定义值e如下。
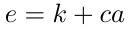
将方程两边与生成元G相乘，我们得到。
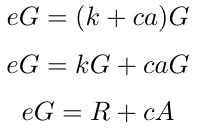
即如果最后方程成立，那么签名有效。协议的正确性已被证明。
安全级别
Schnorr签名方案在secp256k1椭圆曲线上的安全级别为128位，与ECDSA和Ed25519相同。
代码示例
以下是Schnorr签名方案的代码示例。
多方签名计算（又称签名聚合）
Schnorr签名方案的一个价值主张是其支持高级密码技术的能力，例如多方签名计算，也称为“签名聚合”。接下来让我们探讨这一点。
想象一下，Alice和Bob共同合作为一个任意消息m生成签名。每方生成自己的私钥，如同在单方协议中一样。假设Alice的私钥是a_1，而Bob的私钥是a_2。
然后每一方通过将其私钥与生成元G相乘来确定他们的公钥。相应的公钥为A_1和A_2。
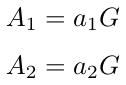
之后，Alice和Bob将他们的公钥相互共享。共享公钥A定义为。
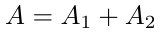
隐式共享私钥a为。
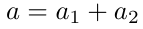
为了共同为消息m生成签名，Alice和Bob还需要生成随机nonces。假设他们的相应_nonce是k_1和k_2，他们的椭圆曲线点R_1和R_2定义如下。
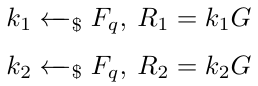
之后，两方将随机点R_1、R_2相互共享。共享随机点R定义为。
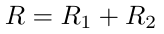
隐式共享nonce为。
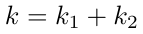
两方接着计算哈希值c如下所示。
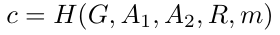
获得到c后，每一方确定值e_1和e_2使得：
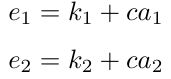
消息m的集体签名是(R, e)，其中。
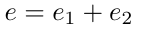
这是为什么呢？我们有。
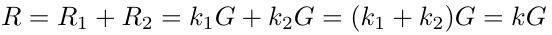
以及
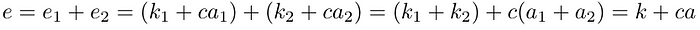
即签名(R, e)确实是私钥a下消息m的签名。协议的正确性得到了证明。
结论
数字签名方案（DSA）是区块链和许多先进密码协议的基本组成部分，例如多方计算（MPC）、可验证随机函数（VRF）和零知识证明（ZKP）。从密码学基础的角度来看，DSA可分为基于椭圆曲线和基于配对的方案。前者即基于椭圆曲线的方案，如ECDSA、EdDSA和Schnorr，在区块链中非常流行且广泛使用。这些方案的安全性依赖于离散对数问题（DLP）的困难性。虽然ECDSA是第一个在区块链中采用的方案，具体是在比特币和以太坊中，但由于其高效性和支持多方签名计算等高级密码技术，EdDSA和Schnorr方案最近获得了重要性。后者即基于配对的方案将在未来的文章中探讨。请持续关注！
如果你觉得这篇文章有见地，请关注我。这将让我非常开心，并激励我写更多优质文章。非常感谢你的支持🙏
参考文献
- 0xbarchitect — 高级密码学原语
- 0xbarchitect — Diffie-Hellman问题，ECDH密钥交换和ElGamal加密协议。
- Nguyen Thoi Minh Quan — 直观的高级密码学
- Andrea Corbellini — 椭圆曲线密码学：ECDH与ECDSA
- Daniel J. Bernstein等 — 高速高安全性的签名
- Philipp Muens — Schnorr签名聚合
- 维基百科 — Curve25519
- 维基百科 — Montgomery曲线
- 维基百科 — EdDSA
- 维基百科 — 椭圆曲线数字签名算法
- 原文链接： medium.com/@barchitect/e...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
