学术研究：我们零知识研究的发现

在 Veridise，我们将前沿的学术研究与最新的行业经验相结合。

除了我们在区块链基础设施协议、智能合约和零知识电路实现审计方面的丰富经验外，我们团队中的许多成员都有学术研究背景。

在这篇博文中，我们展示了我们在 零知识安全 方面的研究，以及它与我们在 Veridise 所做工作的关系。

我们涵盖了以下四篇与 ZK 相关的研究论文：

• 使用精细化类型验证零知识电路
• 零知识证明中的欠约束电路的自动检测
• 零知识证明电路的实用安全分析
• 有限域上满足性模分解 Gröbner 基

以下是我们对每篇论文的总结，以及来自当前 Veridise 团队的作者—点击每个名字以了解更多关于我们的团队成员的信息！

Veridise 的学术研究系列: 📚 第一部分: 来自我们智能合约研究的发现 📚 第二部分: 来自我们零知识研究的发现

使用精细化类型验证零知识电路

Veridise 作者： Bryan Tan, Işıl Dillig

本文论文解决了验证零知识 (ZK) 证明系统正确性的挑战，这对于像隐私保护应用和第二层扩展解决方案（ZK-Rollups）这些安全应用至关重要。

ZK 系统容易出现微妙的错误，这可能使攻击者在未被检测的情况下进行利用，从而使其特别危险。传统的防御措施（例如运行时监控或沙箱）对这样的攻击无效，因为它们不会留下可观察的痕迹。这使得验证和静态分析成为防止这些隐匿攻击的唯一可行解决方案。

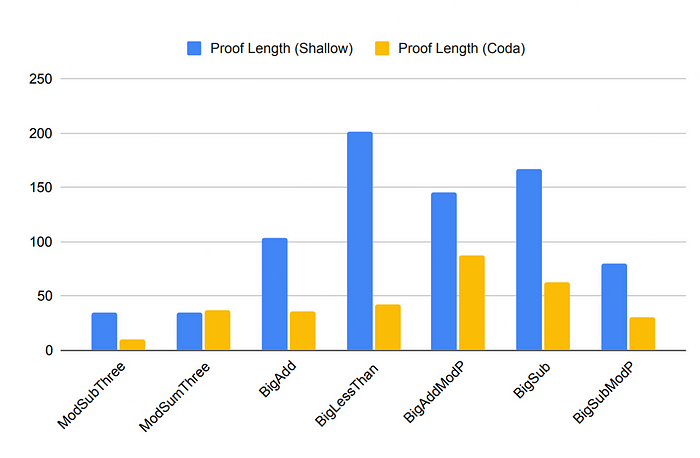
该论文引入了 Coda，这是一个静态类型的函数式语言，允许开发者使用精细化类型系统形式化指定和验证 ZK 应用的正确性。精细化类型通过逻辑公式增强传统类型，从而允许指定更为复杂的正确性属性并实现编译时验证。Coda 允许开发者将规范编写为类型，Coda 的类型检查器验证实施是否符合给定规范。Coda 被用来重新实现广泛使用的 Circom 库和应用中的 79 个算术电路，这一过程揭示了六个先前未知的漏洞。

总体而言，Coda 方法结合了静态分析与交互式定理证明的优点，使其成为区块链安全领域开发者的强大工具。在 Veridise，我们已经使用 Coda 的技术正式定义和验证 ZK 电路在审计项目中的行为，例如 Circom-lib 和 Semaphore。

零知识证明中的欠约束电路的自动检测

Veridise 作者： Shankara Pailoor, Jacob Van Gaffen, Işıl Dillig

这篇研究论文解决了零知识证明中欠约束算术电路的问题，这可能会导致安全漏洞。这些电路由像 Circom 这样的领域特定语言 (DSL) 生成，能够为给定输入接纳多个见证，从而使恶意方能够创建虚假的证明。

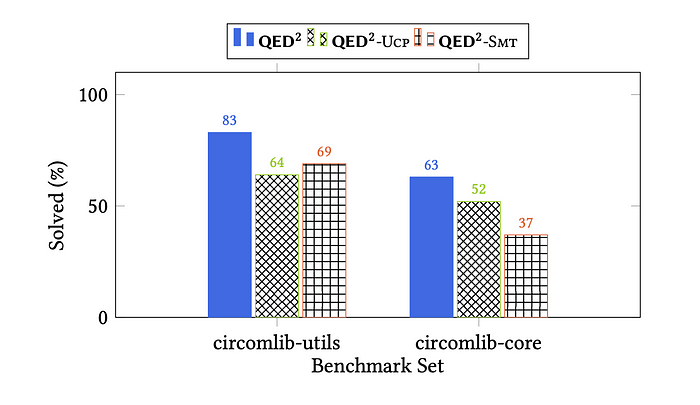
为了解决这个问题，本文引入了 QED2，这是一种新工具，旨在自动检测零知识证明系统中的欠约束电路。QED2 将轻量级唯一性约束传播（UCP）与 SMT（理论可满足性）基于推理相结合，以有效地验证电路是否正当地受到约束。

该工具在Circom库中的163个真实电路上进行了测试。QED2 成功解决了70%的基准，识别出了八个在关键 ZKP 电路中先前未知的漏洞。这展示了这一工具在显著增强零知识证明系统的安全性和可靠性方面的潜力。

在 Veridise，这一研究促使我们开发了内部工具 Picus，旨在检测零知识证明中的欠约束电路。Picus 自此经过多次改进，并扩展到多个额外的 ZK DSL。Picus 经常用于我们的 ZK 审计中，并帮助识别了多个应用和语言中的欠约束电路。

零知识证明电路的实用安全分析

Veridise 作者： Jon Stephens, Kostas Ferles, Shankara Pailoor, Işıl Dillig

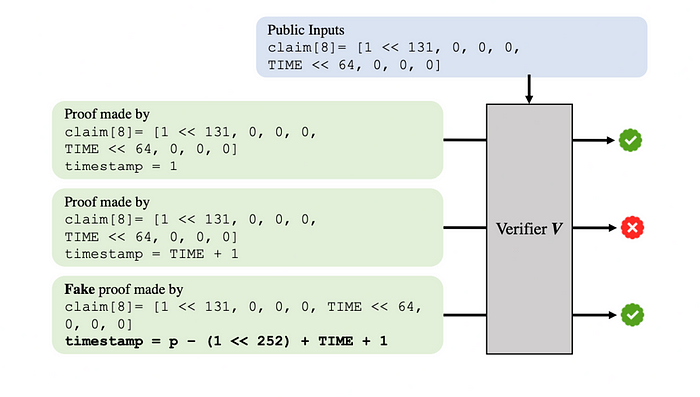
这篇研究论文提出了一种用于检测零知识证明电路中漏洞的轻量级技术，重点关注用 Circom 编写的电路，这是一个流行的领域特定语言 (DSL)。该论文引入了一种静态分析框架，使用一种新的程序抽象称为电路依赖图（CDG），以捕捉电路的关键属性。CDG 抽象有助于高效识别 Circom 程序是否包含漏洞模式。

该工具包括九个不同的检测器，这些检测器在258个电路上进行了评估。评估证明这些检测器能够以高精度和召回率识别漏洞，包括一些先前未知的漏洞，显著提高了 ZKP 电路的安全分析。

在 Veridise，我们已将这项工作集成到我们的 Vanguard 静态分析框架中，并已扩展到其它 ZK 语言。它在 Veridise 的 ZK 审计中经常使用，并识别出多个关键漏洞。

有限域上满足性模分解 Gröbner 基

Veridise 作者： Alex Ozdemir, Shankara Pailoor, Alp Bassa, Kostas Ferles, Işıl Dillig

这项研究论文旨在通过解决以往构建完全 Gröbner 基 (GB) 的解算器的低效率问题，来提高用于加密系统自动验证的解算器的可扩展性。

该论文提出了一种利用多个简单 GB 而不是一个完全 GB 的新解算器，该解算器实现于 cvc5 SMT（理论可满足性）解算器中，并为了解译类似位和的任务引入了专门的传播算法（这些在 ZKP 电路中很常见）。

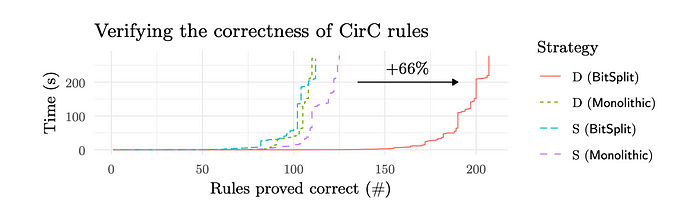
实验结果显示，这种新解算器在处理位和重（bitsum-heavy）确定性基准方面显著超过以往的解算器，并且未对其他类型的基准增加太多开销。

这种方法称为分解 Gröbner 基，其实例化版本 BitSplit，特别适合位和重查询。该方法还被应用于 ZKP 编译器验证，并展现出良好的效果。

在 Veridise，我们将该解算器（引入本论文的想法进行改进）集成到 Picus 工具中，Picus 用于检测欠约束 ZK 电路。当一个电路未被充分约束时，它将转化为一个涉及多项式方程系统的满足性问题。ZK 电路通常位和重，使其成为本文提出的分解 Gröbner 基方法的理想候选。

结论

我们在 ZK 的学术工作产生了以下工具和进展：

• Coda ， 该工具在79个 Circom 电路中揭示了六个先前未知的漏洞。我们已在我们的审计项目中使用 Coda 进行形式验证，例如 Circom-lib 和 Semaphore。
• QED² ， 成功解决了163个基准中的70%，并发现了在广泛使用的电路中八个新漏洞。这篇论文促使我们开发了内部工具 Picus，用于检测 ZK 电路漏洞。
• ZKAP ， 我们的检测器在258个 Circom 项目中识别出漏洞，且具有高精度和召回率，包括几项先前未知的问题。
• BitSplit ， 在处理位和重确定性基准时显著优于以往的解算器，展示了使用多个较简单的 Gröbner 基的有效性。

在 Veridise，我们致力于将学术研究与行业实践相结合，使零知识应用更加健壮和可靠。

感谢你的阅读！如果你还没有机会，你可以阅读我们类似的关于 智能合约安全研究 的博文。

Veridise 的学术研究系列: 📚 第一部分: 来自我们智能合约研究的发现 📚 第二部分: 来自我们零知识研究的发现

作者： Mikko Ikola，Veridise 市场部主管

感谢 Işıl Dillig, Jon Stephens, Bryan Tan, Alp Bassa 审阅本文。

想了解更多关于 Veridise 的信息吗？

Twitter | Lens | LinkedIn | Github | 请求审计

• 原文链接： medium.com/veridise/acad...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～