Distribution Market - 一种新的预测市场

概述

本文介绍了一种新的预测市场——分布市场(Distribution Market )，用于事件，其结果不仅仅是“是”或“否”，而可以是任意数字。

交易者可以表达他们认为每种不同可能性在整个无限结果范围内的可能性，而不是对特定结果或范围进行下注。

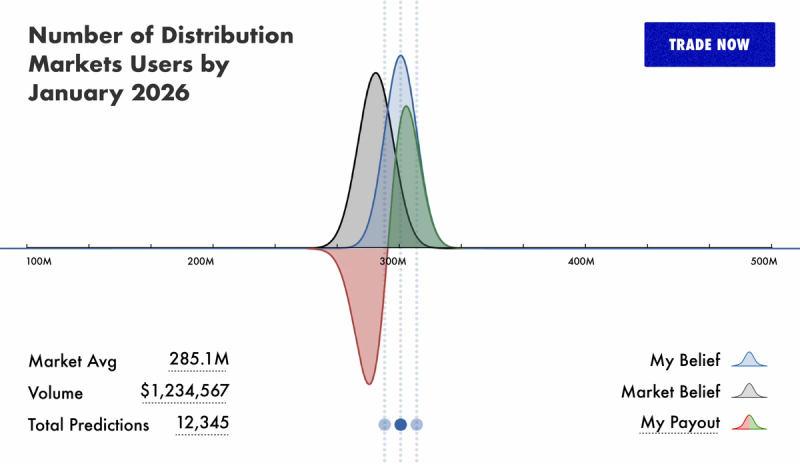
灰色曲线表示AMM的初始信念，蓝色曲线表示一位新交易者的信念，绿色和红色曲线表示如果交易者将市场转移到他们的信念，他们的潜在利润和损失。每条曲线以美元计价，蓝色和灰色曲线是其基础概率分布的标量倍数。

直觉

以“GPT-5何时发布？”为例。在传统预测市场中，交易者可能只能选择“2025年第二季度”或“2026年”这样的预设选项。

与此不同的是，像Metaculus一样的预测竞争让交易者能够以曲线的形式表达他们的预测，准确表示每个可能日期的可能性。然而，Metaculus是一个竞争，而不是市场，没有任何方式让参与者交易他们的信念并通过交易进行更深的参与。

和Metaculus一样，分布市场允许参与者就所有结果的完整概率分布达成共识，但像传统预测市场一样，它们允许交易者通过将共享观点朝正确方向移动而获利。

机制

基本机制是一个常数函数AMM，对于函数来说，不变量（类似于Uniswap的xy=k）是一个常数 $l₂$。

限制在特定分布（如正常分布、对数正常分布等）时，数学 surprisingly 简单，得到的AMM可以高效地在链上实现。

动机

预测市场在2024年美国总统选举后进入了公众意识，但这些技术可能仍处于初级阶段。进一步的发展可能对开发者和公众整体有益。

更具体地说，今天的预测市场通常允许参与者对离散结果表达概率分布，但许多与现实世界相关的问题涉及连续结果。

确实，一个永续合约市场可以从市场中引导出连续变量的期望值，但有时我们想知道更多——例如，我们能否确定某个项目确实需要整整10年，还是它可能在2到20年之间的任何地方？

机制

离散情况

该部分是为理解连续情况提供的辅助，以满足本论文的主要贡献。

我们已经有许多用于离散情况的预测市场AMM选项，在离散情况下，结果是有限选项集中之一。因此，此部分给出的离散情况的分布市场机制并不是特别有用。

然而，离散情况下的数学与连续情况完全相同，因此，本节可能在直觉上有所帮助。

结果代币

考虑某个具有 $N$ 个结果的事件。

我们创建结果代币 X₁,...,Xₙ，其中如果结果是例如结果 i ，则代币 xₜ 的价值为 \$1 ，而其他代币的价值为 $0 。（注意：我们使用美元作为收益货币，以便更广泛受众访问，但这可以是任何资产。）

我们在任何时候都可以铸造和赎回全套这些代币，以便获得 $1，因为在到期时，恰好有一个代币的价值为 $1 ，其余的价值为 $0 。

AMM不变量

我们将创建我们的AMM作为标准常数函数市场制造商（CFMM），其最著名的示例可能是Uniswap，其有常数函数 xy=k。

我们用 k 美元初始化AMM，将其分成 k 每个结果代币，使市场可以销售最多 k 其中任何一个结果代币。

我们将AMM的持有向量表示为 $$ h=k−x=(k−x₁,…,k−xₙ) $$

以便表示AMM已销售的每种结果代币的数量。

我们定义AMM的常数函数为

$$ |x|₂=∑_{i=1}^N x_i²=k $$

因为 $ x=k−h$， 我们也可以写作

$$ |k−h|₂=∑_{i=1}^N (h_i−k)²=k $$

这意味着AMM的持有是以半径 k 为圆心的平移超球体，位于点 (k,…,k) 在 ℝⁿ 中。

请注意，该平移超球体在任何维度上的最小坐标为 0。由此可见，AMM永远不会出售超过 k 个给定结果代币，这是幸运的，因为它没有更多可供销售的东西。

交易行为

假设 $X_i$ 的真实概率分布是 $p=(p₁,…,pₙ)$。 在决策时刻，正确的结果代币的价值将是 1。 因此，AMM持有的期望值是结果代币持有的概率加权总和，$ \sum_i p_i h_i = p⋅h = p⋅(k−x) = k−p⋅x $，其中我们说 $ p⋅k = k $ 因为 p 作为概率分布，和为 1。

如果我们假设市场是有效的，套利者将会为实现自己的持有期望值 $x$ 而采取行动， 这将最小化AMM的持有所值 h。 换句话说，他们正在解决优化问题

$$ min⁡ _x k − p⋅x  s.t. |x|₂=k $$

因为交易者无法影响 k， 这简化为

$$ max⁡_x p⋅x s.t. |x|₂=k $$。

根据Cauchy-Schwarz不等式，给定的固定范数为最大化该点积的向量必须是与 $p$ 线性相关的。

这意味着我们必须有 $$ x=k\frac{p}{|p|₂} $$ 。

换句话说，x， 市场共同持有的持仓向量，直接与真实概率分布 $p$ 成正比，比例为其 $ l₂ $ 范数为 k。

根据上面的定义，AMM的持有量 h 由以下关系确定：

$$ h=k−x=k(1−\frac{p}{|p|₂}) $$

这有一个好的副作用，即我们可以从AMM的储备中直接读取市场的估计分布。

通过这种方式，分布市场是一个市场计分规则 的例子。

连续情况

连续情况是本论文的主要贡献，因为它解锁了一种新的行为：对连续概率分布的预测市场式交易。

该机制与离散情况几乎完全相同，但增加了一些约束，以确保市场保持偿付能力。

这是一个一般性构造，但通过特殊化允许的分布类型——例如均匀或高斯分布——得到的AMM可以在以太坊主网高效运行。我们将在下面更详细地讨论这一点。

结果函数代币

考虑某个在连续空间上具有结果的事件，例如 $ℝ$。

我们可以想象为连续空间中的每个点 $x∈ℝ$ 创建一个结果代币 X， 使得如果结果为 x，那么该结果代币将可兑换 $1，而其他代币的价值为 $0。

表达这些代币持有的最简单方法是作为函数 $ f:ℝ→ℝ⁺$， 其中 $ f(x) $ 是持有 $f$ 的所有者对于结果$ x $ 持有的代币数量。 换句话说，持有 $f$ 的持有者在结果为 $x$ 时，将获得 $f(x)$。

正式而言，所有在连续预测市场中的头寸都是函数。根据上下文，可能最有帮助的是将这些函数视为结果代币的无限集合、曲线，或者只是作为函数空间的抽象成员。

铸造和赎回

考虑常数函数 $f(x)=b$。无论结果 $x₀$，持有此函数的持有者在决策时刻将获得 $f(x₀)=b$。 因此，我们在任何时候允许该函数以 $b$ 美元铸造或赎回。

AMM不变量

与离散情况一样，我们将使用固定金额的美元初始化我们的AMM， $b$。

我们将AMM的持有结果函数表示为 $h(x)=b−f(x)$。

AMM可以在任意给定的点 $x₀$ 销售最多 $f(x₀)=b$，因为在结果确定后，它将在该点移交 b。 当时，我们将有 $h(x₀)=b−b=0$，表示AMM无法再出售该结果。

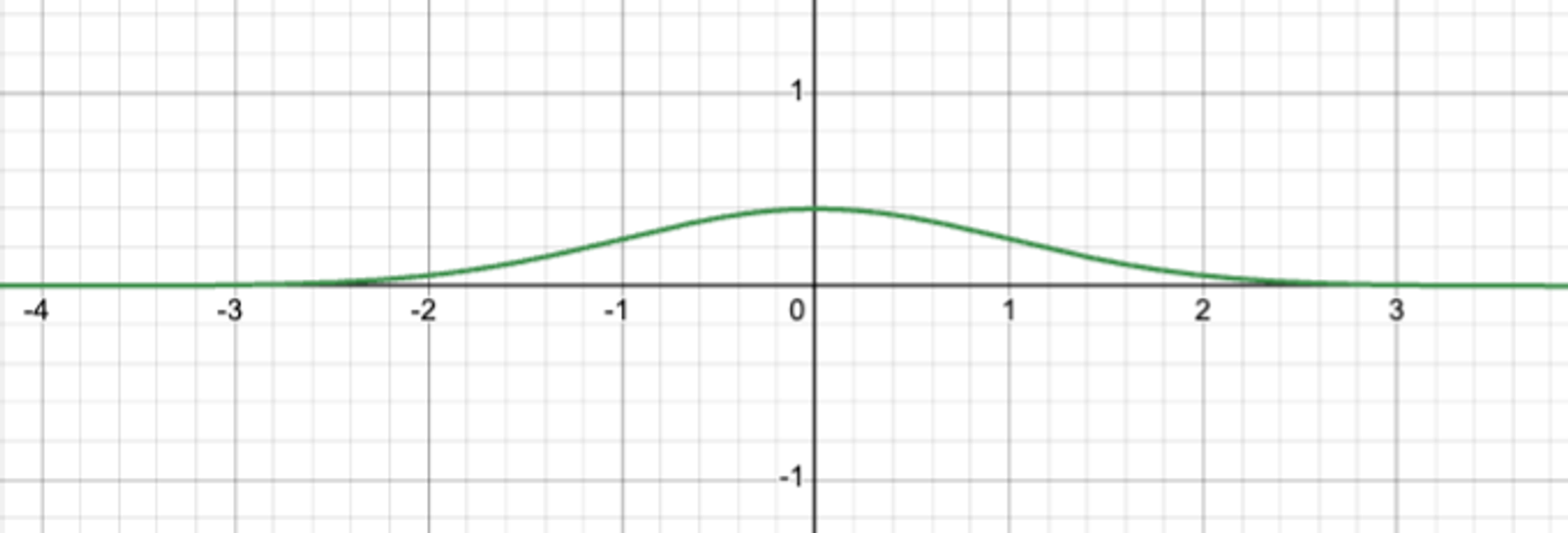
如果交易者在整体上从AMM购买了结果函数 f(x) ...

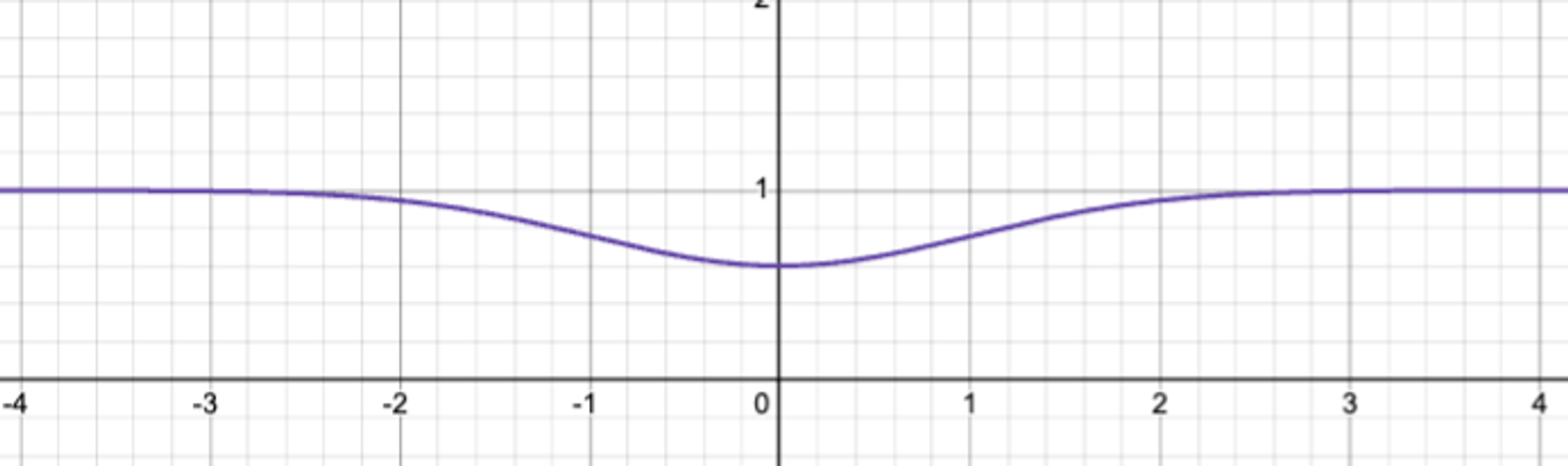
...AMM的持有量 h(x) 为 b-f(x)。

我们限制 f 位于 $L²$， 这是平方可积函数的空间（即平方具有有限积分的函数）。这是一个内积空间，其内积为 $$f⋅g=∫Rf(x)g(x)dx$$。

与离散情况一样，我们将选择常数 $l²$ 范数作为我们的常数函数。 在这个空间中，该常数表示为

$$ |f|²=∫Rf(x)²dx=k $$。

请注意，我们在此处将 $l²$ 范数限制为一个新常数 $k$， 而非 $b$， 我们初始化AMM的金额。 在有限维情况下，没有一个具有 $ l₂ $ 范数的向量 x 的值超过 $k$， 因此，我们的 $l₂$ 范数约束足以确保AMM的偿付能力。在无限维情况下，这不再是真的。因此，我们将备据信息 $b$从 $l²$ 范数约束 $k$ 中分离出来， 并向AMM添加了一个额外的约束，即$ max ⁡f≤b$。

交易行为

AMM开始时持有某个函数 $h(x)=b-f(x)$。

当交易者希望将市场移动到 $g(x)$， 使得AMM现在持有 $b−g(x)$，时，他们最终将持有 $g(x)−f(x)$，

两个函数的差值。

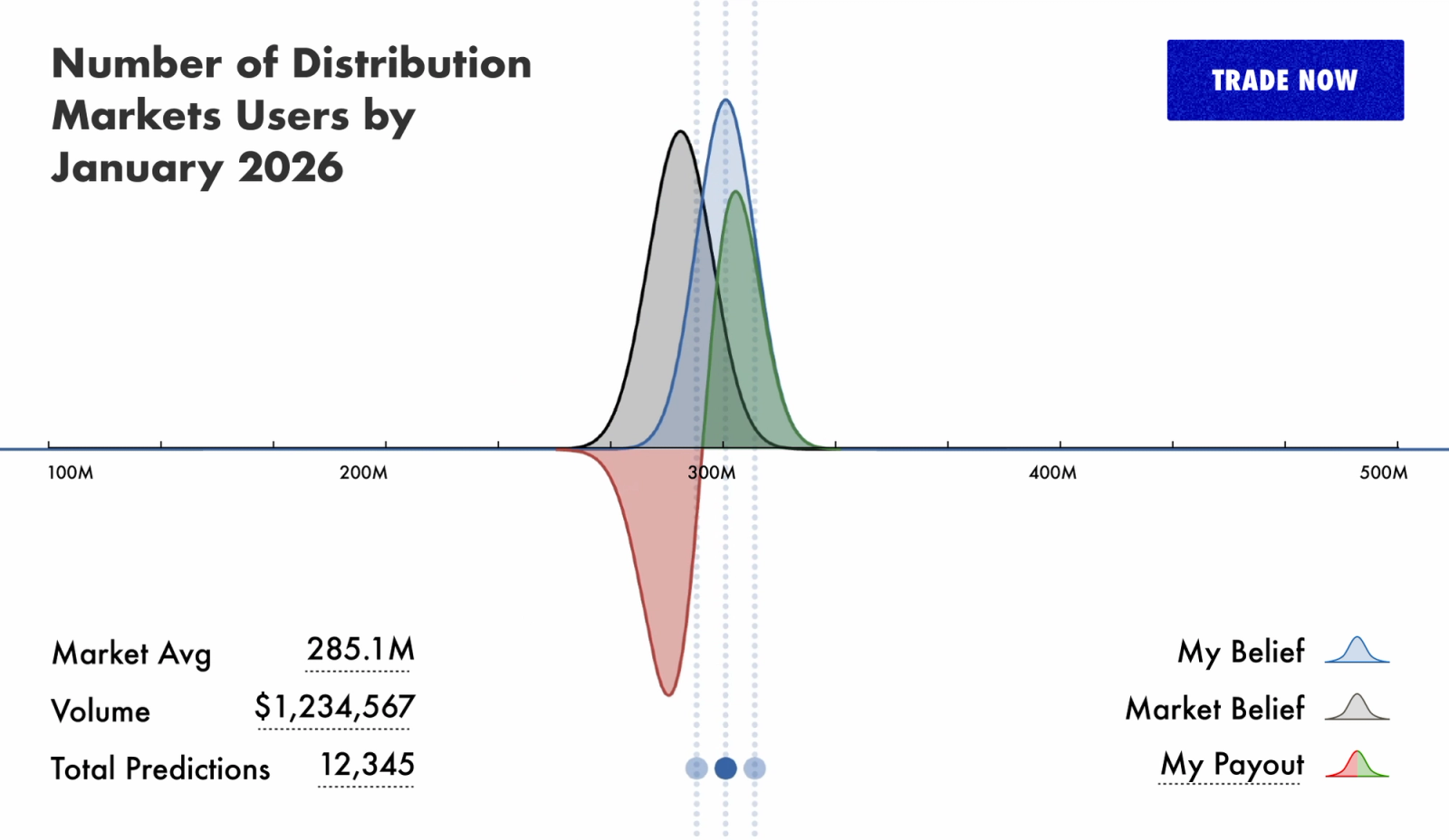
灰色曲线是初始 $f(x)$， 该位置初始由所有交易者持有，是市场对真实分布初始估计的标量倍数。 蓝色曲线是 $g(x)$， 交易者正将市场移动到该分布的标量倍数，导致适当的 $l₂ $ 范数。 绿色和红色曲线是 $g(x)−f(x)$，

表示交易后交易者的持仓。如果结果在绿色区域，他们将赚钱，而在红色区域则会亏损。我们可以看到，他们稍微降低了均值并增加了方差，因此他们一般来说如果结果在原始曲线的峰值区域之外时会获利。

更正式地，假设该结果的真实概率分布由概率密度函数描述为

$p(x)$，

因此AMM持有的期望值是

$E(b−f(x))=b−E(f(x))=b−∫Rf(x)p(x)dx=b−f⋅p$

其中最后一个等式来自我们在此空间内积的定义。

如果市场有效，套利者将采取措施最大化AMM的期望值。换句话说，他们正在解决优化问题

$min⁡f b−f⋅p s.t. |f|²=k 和 max⁡f≤b$。

因为交易者无法影响

$b$， 这简化为

$max⁡f f⋅p s.t. |f|²=k 和 max⁡f≤b$。

Momentarily, 假设AMM具有有效的无限背书，以致于第二个约束无关紧要，我们仅仅需要

$max⁡f f⋅p s.t. |f|²=k$。

然后，与离散情况一样，Cauchy-Schwarz不等式告诉我们，在给定固定范数的情况下，有效最大化该点积的向量必须与 $p$ 线性相关——换句话说，我们知道我们必须满足

$f=k\frac{p}{|p|²}$。

换句话说，f， 交易者共同持有的结果函数，直接与真实概率分布成正比！

这意味着AMM的持有量 $h$ 由以下关系确定：

$h=b−f=k(1−\frac{p}{|p|²})$，

我们同样可以直接从AMM的储备中读取交易者的整体估计分布。

如果真实分布$p(x)$ 看起来像这样……

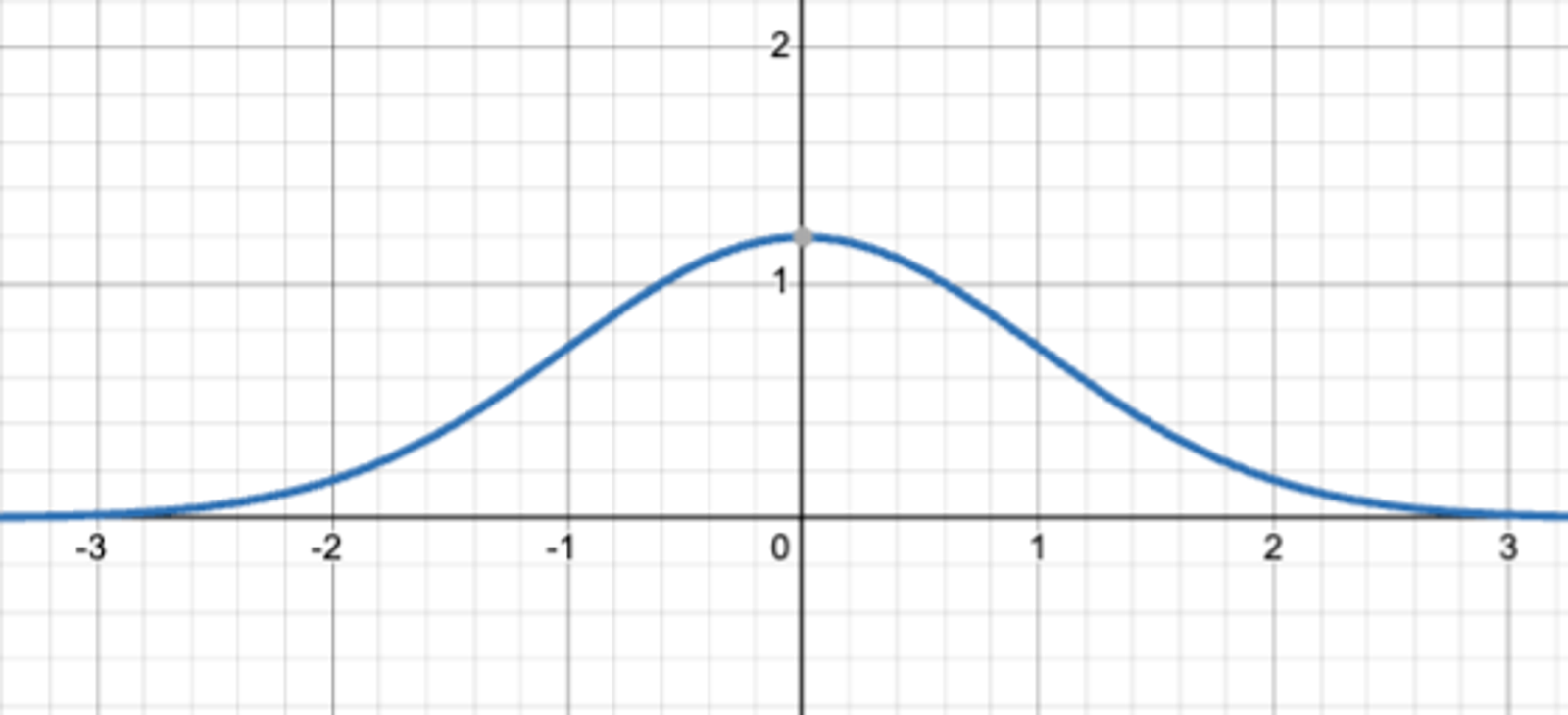
在有效市场中，交易者的持股 f(x) 将在整体上成比例地…

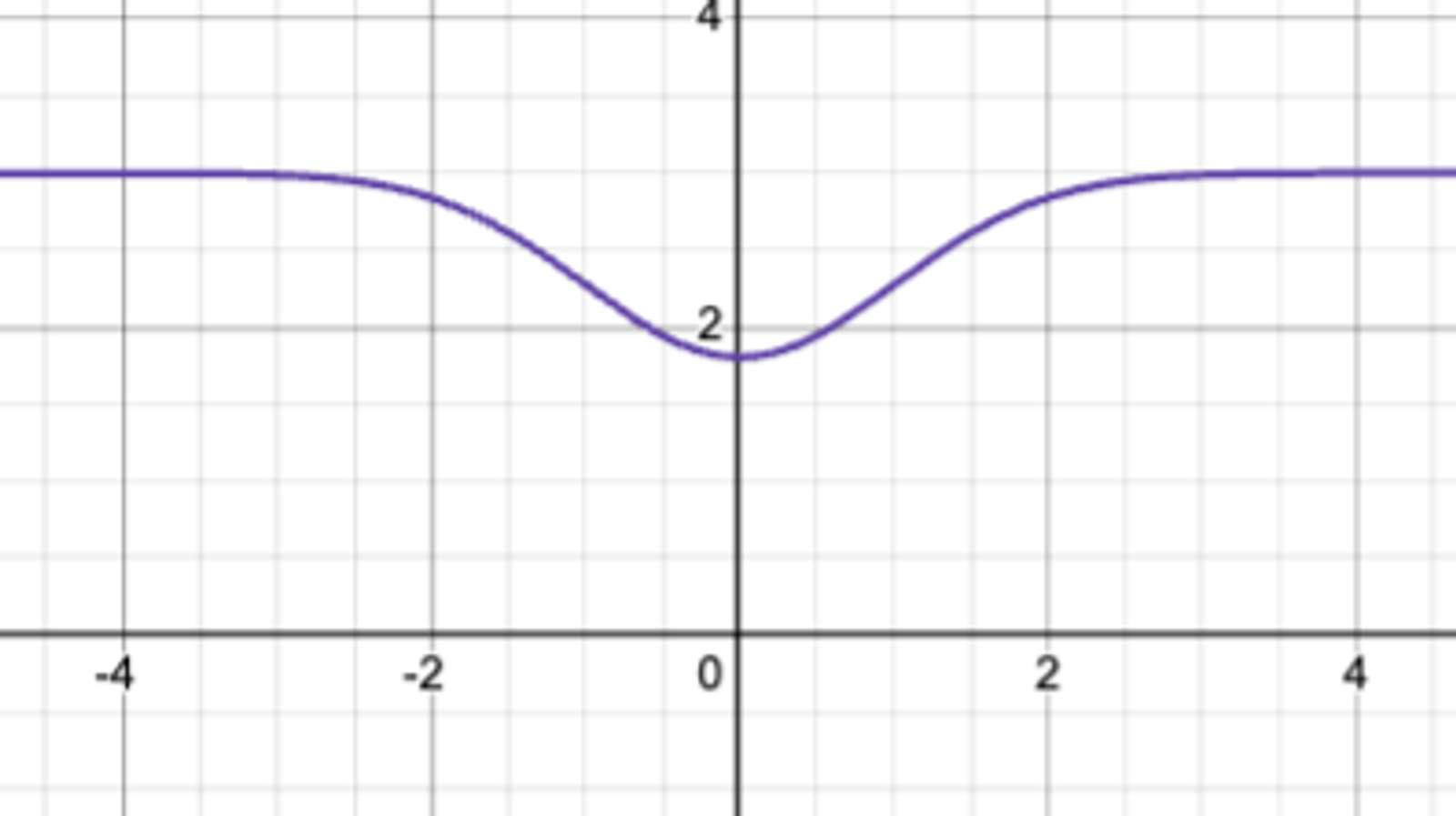
……而AMM的持股$h(x) $ 将是镜像。

处理备付约束

我们以上假设AMM的备付金 $b$将为无限，但当然，这通常不是案例。

当存在备付约束时，我们有两个选择：

第一种方法，最简单，便是不允许交易者将 $f(x)$ 移动到未满足 $|f|²=k$ 但 $max⁡f>b$。

在正常情况下，正如下文所述，这简单意味着阻止交易者估计过窄的标准差，这可能是适合帮助市场避免被内部消息的交易者信息洗劫的。

另外，我们可以简单地强制执行约束 $f(x)≤b$。

假设交易者认为真实的概率分布是 $p(x)$。

我们将留给读者练习以表明交易者的最佳持有将是

$f(x)=min⁡(λp(x),b)$，其中任何 $λ$ 使得此地方满足

$|min(λp(x),b)|²=k$。

我们可以在链外数值上查找 $λ$

并且对于许多分布，轻松地在链上验证这个属性。

流动性提供

AMM允许无权限的流动性添加，流动性提供者（LP）获得可互换的LP份额，像在Uniswap V2中一样。

想象一下我们有一个包含10,000 USDC和1 ETH的Uniswap V2池，其中有10,000 LP份额存在。如果市场参与者想要向此池中添加流动性，他们需要添加代币，这些代币是AMM持仓的标量倍数，并且返回相应比例的池份额。因此，例如，如果新的流动性提供者翻倍池中的流动性，他们可以添加10,000 USDC和1 ETH，并获得10,000 LP份额。

流动性提供在分布AMM中同样方式工作。潜在的流动性提供者需要添加与AMM当前持仓成比例的资产，并获得LP份额作为回报。

AMM的持仓为 $h=b−f$。因此，想要添加当前流动性的一部分 $y$ 的 LP 需要贡献一个持仓 $yh=yb−yf$。

作为回报，他们将获得 $yl $ LP份额，其中$l$ 为当前已发行的LP份额数量。

为了创建持仓 $y$ 我们需要要求 LP 使用 $yb$ 作为抵押进行铸造。 这意味着他们将保留一个持仓 $yb−yh=yb−(yb−yf)=yf$，

代表市场在铸造他们的LP份额时的持仓。

抵押

AMM的初始抵押来源是第一个LP。如果他们以 backing $b$ 初始化池，他们需要提交 $b$ 作为抵押。他们还将为池指定一些初始 $f$， 以便池的持仓为 $h=b−f$，初始LP保留持仓 $f$。 AMM的持仓与所有交易者的持仓总和为 $b$， 并且有 $b$ 做抵押，因此系统是完全抵押的。

同样，当新的LP添加流动性时，他们将为池添加 $yb−yf$， 并为自己保留$ yf$。从一开始，他们将增加 $yb$，到整体已发行持有量，因此只要他们提供 $yb$ 作为抵押，系统将保持完全抵押。此外，如果AMM的持仓和所有交易者的持仓在添加流动性之前总和等于备付金额，那么该平衡在之后仍将成立。

最后，假设在交易进行时，系统完全抵押，且AMM的持仓与所有交易者的持仓和等于 $b$。 当前市场持有 $h=b−f$， 交易者将市场转移到 $h₂=b−g$，因此，这位交易者现在应持有 $g−f$。 如果是这样，因为我们知道所有其他交易者共同拥有 $f$， 则所有交易者的总持仓将为 $f+(g−f)=g$，这意味着所有交易者与市场一起持有的总和将为 $b−g+g=b$，市场仍然是完全抵押的。

然而，为了说交易者持有 $g−f$，在结果为$x₀$ 时，他们必须失去资金，如果我们有 $g(x₀)−f(x₀)<0$。 因此，交易者必须用 $−min⁡x(g(x)−f(x)) $ 作为抵押。 我们将在下面与正常情况相关的部分探讨如何验证这一点。

正常分布情况

概述

正常分布（normal distribution 也可以翻译为正态分布 ）在某种程度上是连续概率分布的典型示例。

在本节中，我们将讨论如何使用分布市场在链上高效地创建针对正态结果的预测市场。

l₂范数

均值为 $μ$ 和标准差为 $σ$ 的正常分布具有概率分布函数

$p(x)=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x−μ)²}{2\sigma²}}$，

其 $l²$ 范数为

$ \sqrt { \int_ℝ \frac{1}{2\pi \sigma²} e^{-\frac{(x−μ)²}{\sigma²}} \, dx }= \sqrt{\frac{1}{2\sigma\sqrt{\pi}}}$。

后一个等式来自于高斯积分的封闭形式解。

AMM行为

我们可以看到， $l²$ 范数与分布的均值无关，因此我们的AMM对标准差相同但均值不同的分布无动于衷——交易者可以将市场移动到他们希望的任何均值，同时保持相同的标准差，只需提供适当的抵押。 在以后的工作中，我们可能会探索将AMM赋予一个先验，这样可以更倾向于某些均值。

然而，方差较低的分布具有更高的 $l²$ 范数。这意味着如果市场估计的正常分布的标准差为 σ， 则有 $$ k=∣∣f∣∣²=∣∣λp∣∣²=λ∣∣p∣∣²=λ \frac{1}{2\sigma\sqrt{\pi}} $$。 因此， $$λ=\frac{k²}{2π}$$。

换句话说，交易者提出的分布越尖锐，市场愿意出售给他们的总概率质量就越小。这可能帮助市场避免被有关于特定结果的内部信息的交易者洗劫。

备付约束

请记住，我们有 $f=λp$，而 $p$ 为正态概率密度函数。在其峰值时， $p$ 的值为

$\frac{1}{\sqrt{2\pi\sigma²}}$。 作为 $p$ 的倍数，$f$ 具有最大值

$$ \max⁡f=\frac{λ}{\sqrt{2\pi\sigma²}} = k\sqrt{2\sigma\sqrt{\pi}} \frac{1}{\sqrt{2\pi\sigma²}} = k\sqrt{\frac{1}{\sigma\sqrt{\pi}}} $$

由于我们永远无法得到 $f(x)>b$，这意味着我们必须有 $$ \max⁡f=k\sqrt{\frac{1}{\sigma\sqrt{\pi}}}≤b $$

如此一来

$$ σ≥\frac{k²}{b²\sqrt{\pi}} $$

如上所述的一般连续情况下，我们可以简单地限制AMM中的交易者选择标准偏差小于此值。

另外，我们可以让交易者以愿意的标准差交易限价高斯分布，使得我们有 $f(x)=\min(b,λϕ(x))$

对于满足 $l² $ 范数的任何 $λ$。

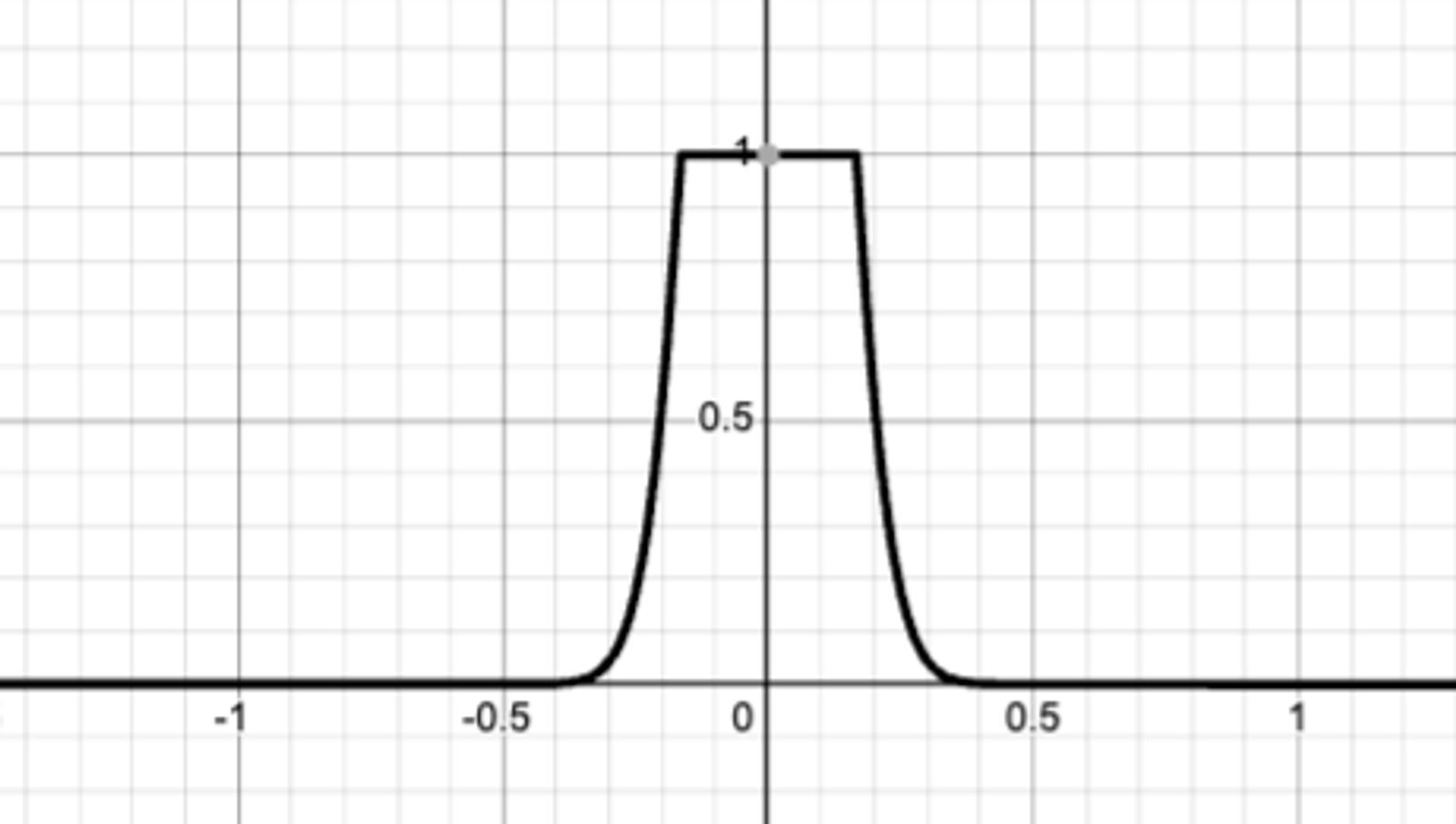
我们可以限制交易者的支付为 $b$ …

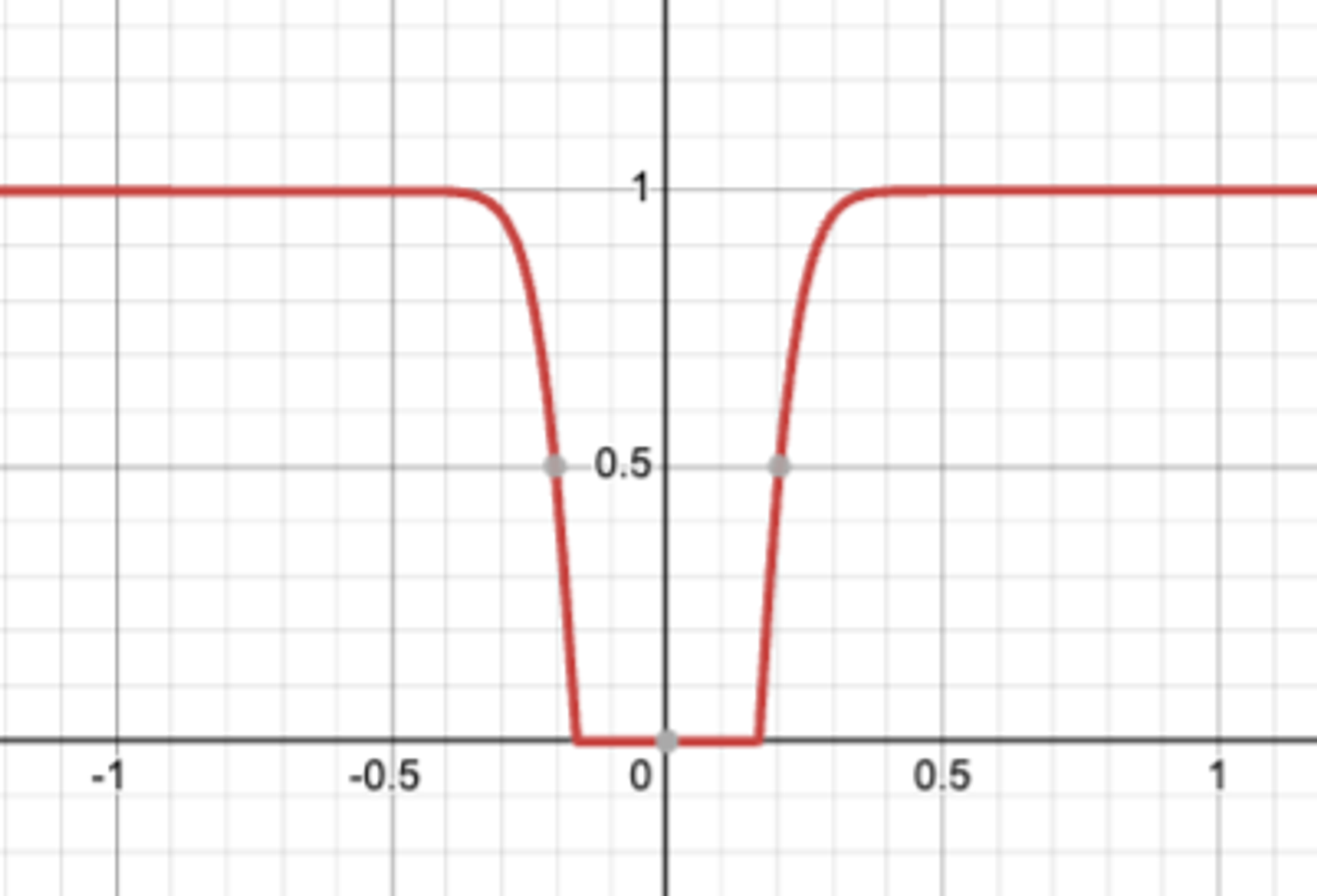
……这样AMM的支付在最小值为0。

然而，在本文的剩余部分，我们将假设我们在简单起见时在 $σ$ 上施加下限。

抵押

如上讨论的一般连续情况的抵押部分所述，交易者需要用 $−min⁡x(g(x)−f(x))$ 进行抵押，将AMM从 $h=b−f $ 移动到 $h₂=b−g$。

不幸的是，没有明显的封闭形式解来表示 $min⁡x(ap−bq)$， 其中$p$和$q$是正态概率密度函数。 然而，我们可以数值计算这一最小值。 尽管可能存在多个局部最小值，但事实证明，只有远离$q$ 的均值的对立面会是全局最小值（证明只能存在一种这样的点是一个非常有趣的练习）。 然后，我们可以通过检查一阶和二阶导数，验证交易者在链上提供了这一点（并确保总的最大亏损至少是某个“粉尘”量以避免数值攻击），并要求提供相应的抵押金额。

$$ m=\frac{λ′}{2σ_q\sqrt{\pi}}-\frac{λ}{\sqrt{2\pi(\sigma_p²+\sigma_q²)}}e^{-\frac{(μ_p−μ_q)²}{2(\sigma_q²+\sigma_p²)}} $$

多重分布

请注意，我们可以有单一分布AMM能够交易多种分布——只要满足 $l₂$ 范数约束和最大损失约束，没有理由不允许交易者从例如正常分布转向均匀分布进行单笔交易。 实际上的主要难题在于计算交易抵押。

在正常分布->均匀分布和均匀分布->正常分布情况下，这相对简单。我们将这些计算留给读者的练习。

结论

我们希望分布市场能激励前沿信息金融领域的建设者和研究者的创意。

如果你就是这样的人，我们很想听到你的想法。

致谢

Dan Robinson， Yang You， Achal Srinivasan， Bhargav Annem， 5/9， Sofiane Larbi， Ciamac Moallemi， Tom Dean， andnasnd， 0xTomoyo， Pia Park， Qiaochu Yuan， Connor Lurring， Grant Stenger， Santiago Lisa

• 原文链接： paradigm.xyz/2024/12/dis...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～