掌握一阶约束系统 R1CS 及其在 Circom 中的示例

  • thogiti
  • 发布于 2023-10-19 17:48
  • 阅读 36

本文详细介绍了Rank-1 Constraint Systems (R1CS) 在零知识证明中的应用，通过多个实例展示如何构建R1CS，使用Circom和snarkjs工具实现电路，并提供了数学公式的详细推导与代码实现。文章涵盖了R1CS的基本定义、与逻辑门电路的关系、构造方法以及多个示例，包括相应的约束解析和代码实现，具有较强的实用性和技术深度。

概述

Rank-1 约束系统（R1CS）是加密协议中的一个关键组件，特别是在与零知识证明（如 zk-SNARKS）相关的协议中。它们是一组方程，用于表示计算，尤其在我们想证明某个计算是正确的，而不揭示关于输入或计算本身的任何其他信息的场景中很有用。

在 zk-SNARKS 的上下文中，一个算术电路被转换为 R1CS。R1CS 中的每个约束对应于电路中的一个逻辑门。"rank-1" 指的是在这个转换过程中生成的矩阵的秩。

在 之前 的博客文章中，我们看到了创建零知识证明系统的流程。以下是该流程的高级视图：

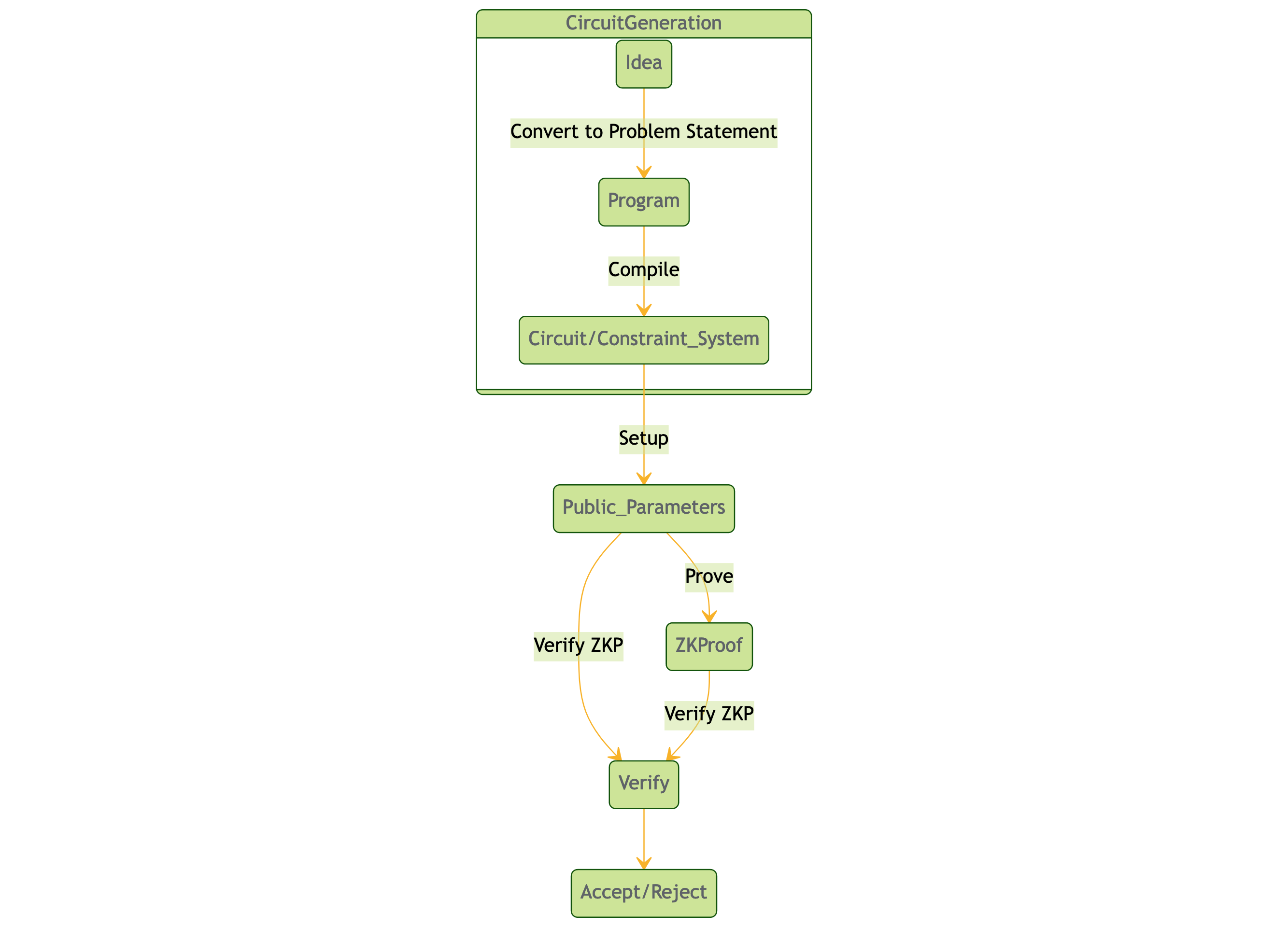
零知识证明流程图

约束系统是一组针对一组变量的算术约束的集合。它们在计算问题中扮演了重要角色，特别是在加密协议和零知识证明的领域。在约束系统中，变量分为两类：高层变量（秘密输入）和低层变量（乘法门的内部输入和输出）。

理解 R1CS 在 ZK 协议中的角色

零知识（ZK）协议通常用于加密中，要求证明者证明他们知道计算问题的解。这个问题通常表示为 Rank-1 约束系统（R1CS）。

R1CS 本质上是一组关于一组变量（也称为信号）的非线性算术约束。R1CS 的安全性主要依赖于其非线性组件，因为这些部分是系统中攻击者解决难度较大的部分。

相比之下，虽然线性（加法）约束是系统的一部分，但对其安全性没有显著贡献。这是因为这些约束相对容易解决，无法有效防御潜在攻击。

R1CS 的定义与说明

Rank-1 约束系统 (R1CS) 是一种特定类型的约束系统。它由两类约束组成：乘法约束和线性约束。每个乘法约束的形式为 a_L * a_R = a_O，而每个线性约束的形式为 W_L * a_L + W_R * a_R + W_O * a_O = W_V * (v + c)。其中，a_L、a_R 和 a_O 分别表示电路中每个门的左输入、右输入和输出。W_L、W_R、W_O 和 W_V 是施加于相应输入和输出的权重。

与逻辑门电路的关系

在 zk-SNARKs 的上下文中，一个算术电路被转换为 R1CS。每个约束对应于电路中的一个逻辑门。这种转换至关重要，因为 zk-SNARKs 要求计算问题表示为一组二次约束，这与逻辑门电路息息相关。

为零知识证明构造 R1CS

我们将深入探讨多个示例，说明如何为给定的多项式方程或语句构造 Rank-1 约束系统 (R1CS)，特别是在创建零知识证明时。

我们将使用 Circom 和 snarkjs，这两个强大的工具可以帮助表示和处理非线性和线性约束。这将帮助我们理解电路是如何编译的以及见证如何被生成。

请注意，要跟随本教程，你需要安装 snarkjs 和 Circom。你可以使用以下 Node.js 命令安装它们：

npm install snarkjs

有关 Circom 安装的文档，请参阅官方文档 docs.circom.io.

Circom R1CS 示例

在我们可以创建 r1cs 之前，我们的多项式和约束需要成为以下形式

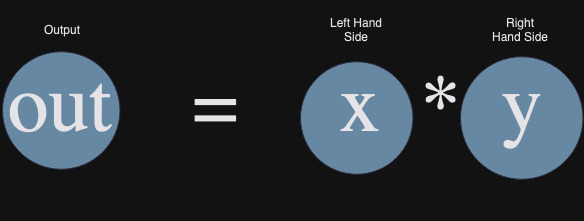
r1cs-form

此外，Circom 期望约束的形式为 $Aw * Bw - Cw = 0$，其中 $A$ 是矩阵的左侧，$B$ 是矩阵的右侧，$C$ 是输出矩阵的形式。变量 $w$ 是见证向量。这里见证 $w$ 将成为 $[1, out, x, y, ...]$

矩阵 $A$、$B$ 以及 $C$ 的列数与见证向量 $w$ 相同，每一列代表相同的变量索引。

我们将看到并通过 Circom 验证这种形式，当我们编译 Circom 电路并查看关于约束的信息时。

示例 1

电路 $out = x*y$

Ex1 R1CS 约束说明

由于我们的方程已经处于二次约束形式，即 $out = x y$ 或 $AB-C=0$，其中 $x$ 是左侧矩阵 $A$，$y$ 是右侧矩阵 $B$，而 $out$ 是结果矩阵。

见证 $w$ 将是 $[1, out, x, y]$。

请记住，矩阵 $A$、$B$ 和 $C$ 将与见证向量 $w$ 共享相同的列。

$A$ 为 [0, 0, 1, 0]，因为只有 $x$ 目前存在，且多项式中没有其他变量。 $B$ 为 [0, 0, 0, 1]，因为右侧的变量仅为 $y$。 $C$ 为 [0, 1, 0, 0]，因为我们只有 $out$ 变量。

现在，我们可以验证 $Aw * Bw - Cw = 0$。

Ex1 Sagemath 实现

你可以通过运行以下 Sagemath 代码来验证上述矩阵的计算。

## 定义矩阵
C = matrix(ZZ, [[0,1,0,0]])
A = matrix(ZZ, [[0,0,1,0]])
B = matrix(ZZ, [[0,0,0,1]])

x = randint(1,100000)
y = randint(1,100000)
out = x * y

## 见证向量
witness = vector([1, out, x, y])

## 计算结果
A_witness = A * witness
B_witness = B * witness
C_witness = C * witness
AB_witness = vector([A_witness.dot_product(B_witness)])

## 打印结果
print(f"A * witness = {A_witness}")
print(f"B * witness = {B_witness}")
print(f"C * witness = {C_witness}")
print(f"(A * witness) * (B * witness) = {AB_witness}")

## 检查等式
result = C_witness == AB_witness
print(f"result: ",result)

## 检查等式是否成立
assert result, "result contains an inequality"

输出将如下所示：

A * witness = (15189)
B * witness = (90533)
C * witness = (1375105737)
(A * witness) * (B * witness) = (1375105737)
result:  True

Ex1 Circom 电路实现

此电路的 Circom 电路模板如下所示：

pragma circom 2.1.4;

template Multiply2() {
    signal input x;
    signal input y;
    signal output out;

    out <== x * y;
 }

component main = Multiply2();

/* INPUT = {
    "X": "5",
    "y": "77"
} */

让我们使用 Circom 编译器编译此文件并创建 r1cs 文件。在终端运行以下命令。

circom multiply2.circom --r1cs --sym
snarkjs r1cs print multiply2.r1cs

来自上述命令的输出如下所示：

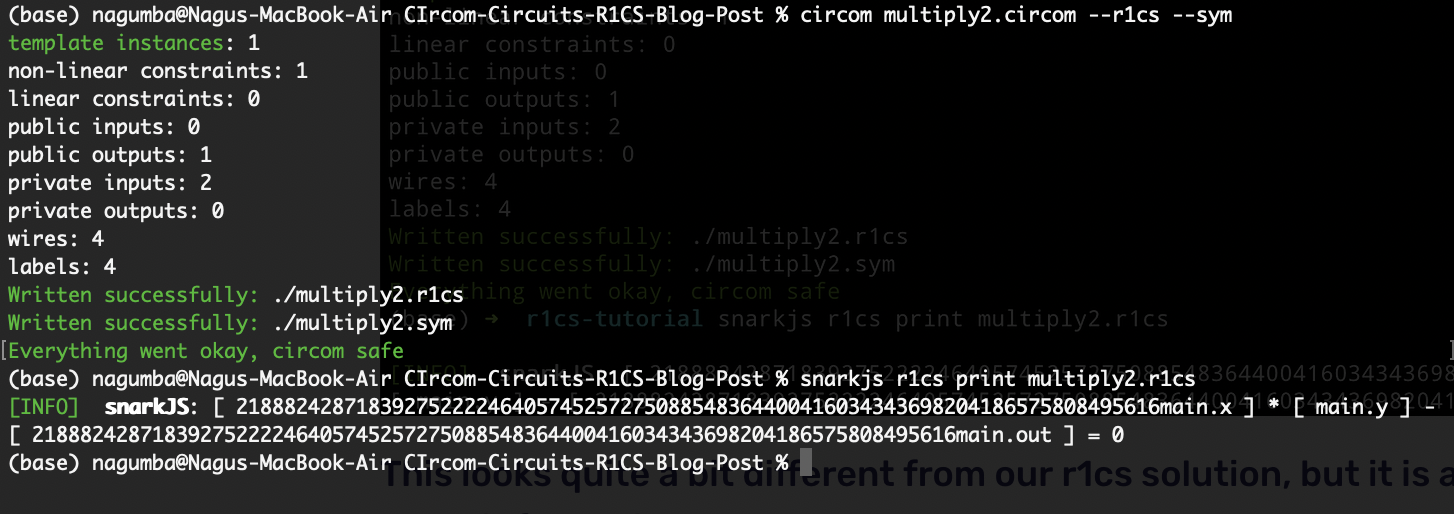
multiply2-r1cs

我们应该期望约束以 $ A * B - C = 0 $ 的形式出现。

  • 为什么我们会看到这个非常大的数字 21888242871839275222246405745257275088548364400416034343698204186575808495616？
  • 这个数字是什么？

在 Circom 中，数学是以模 21888242871839275222246405745257275088548364400416034343698204186575808495617 进行计算的。上述数字 21888242871839275222246405745257275088548364400416034343698204186575808495616 在 Circom 中等价于 -1。 

p = 21888242871839275222246405745257275088548364400416034343698204186575808495617

## 1 - 2 = -1
(1 - 2) % p

输出如下：

21888242871839275222246405745257275088548364400416034343698204186575808495616

所以，snarkjs 命令的输出等价于 $out - x*y =0$。

我们的矩阵是：

$A = [0, 0, -1, 0]$, $B = [0, 0, 0, 1]$, $C = [0, -1, 0, 0]$

让我们使用 wasm 求解器重新编译我们的电路：

circom multiply2.circom --r1cs --wasm --sym

cd multiply2_js

我们创建 input.json 文件：

echo '{"x": "11", "y": "9"}' > input.json

现在，计算见证：

node generate_witness.js multiply2.wasm input.json witness.wtns

snarkjs wtns export json witness.wtns witness.json

cat witness.json

我们可以检查 Circom 是否使用了与我们一直使用的见证 $w$ 相同的列布局：$[1, out, x, y]$，因为 $x$ 在我们的 input.json 文件中被设置为 11，$y$ 被设置为 9。

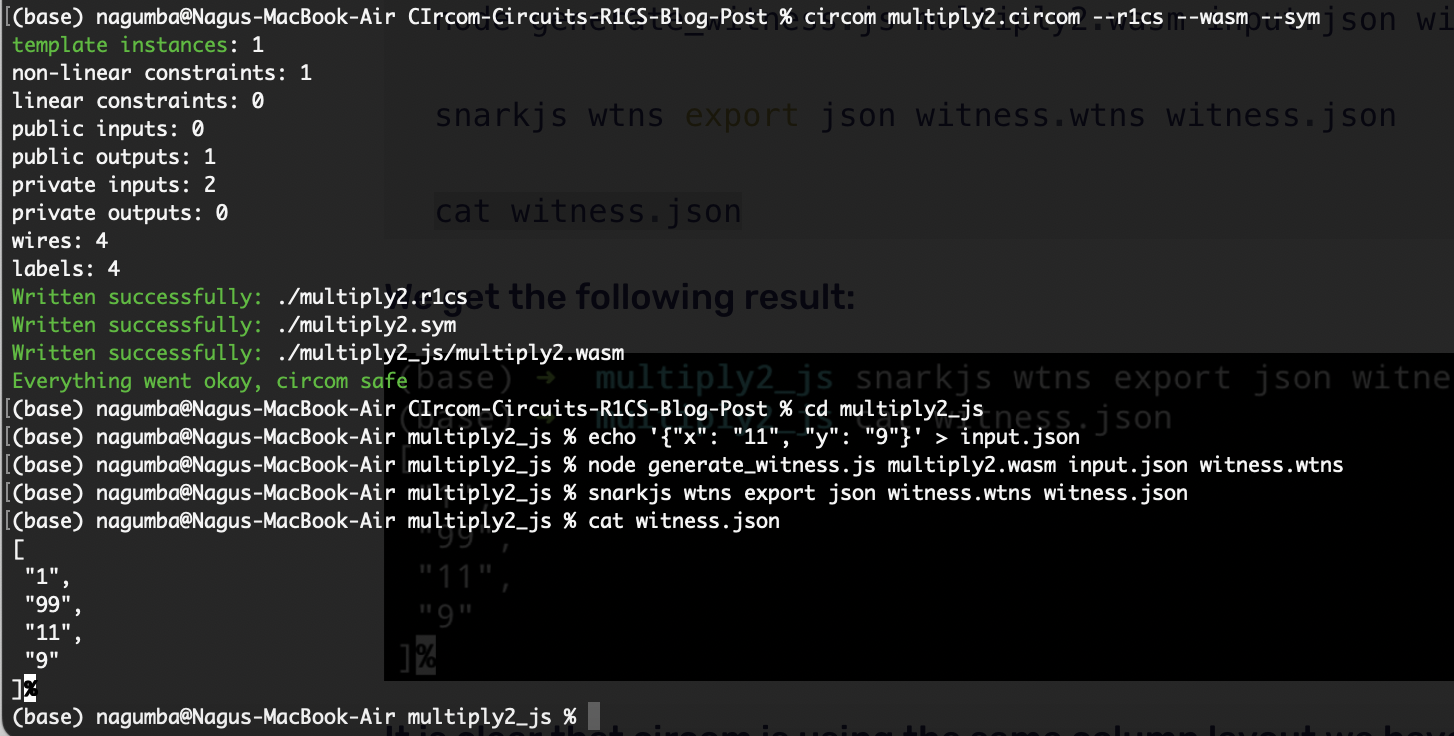
multiply2-r1cs-wasm-witness

在 multiplier2 电路中，我们使用了 x 和 y（2 根线），将它们与信号 out（+1 根线）连接，以及另一根（+1 根线）作为 out 的输出，并检查当 out <== x * y 时只有 1 个约束。因此，我们有 4 根线和 1 个约束。

我们可以手动检查我们的矩阵是否满足约束 $Aw*Bw = Cw$。

$w = [1, 99, 11, 9]$, $A = [0, 0, -1, 0]$, $B = [0, 0, 0, 1]$, $C = [0, -1, 0, 0]$

$Aw = -11$, $Bw = 9$, $Cw = -99$, $Aw*Bw = -99$。

示例 2

电路 $out = {x y u * v}$

Ex2 R1CS 约束说明

请记住，在 R1CS 中，你最多只能在约束中有一个乘法。上述方程有三个乘法。我们使用中间变量将多项式扁平化如下。

$$u1 = x y$$ $$u2 = u v$$ $$out = u1 * u2$$

见证向量将是 $[1, out, x, y, u, v, u1, u2]$。这使得我们的矩阵 $A$、$B$ 和 $C$ 将具有八列，与 $w$ 的列数相同。

我们有三个约束，因此在矩阵 $A$、$B$ 和 $C$ 中将有三行。每一行代表上述平衡关系中对应的约束。

r1cs-ex2

构造矩阵 A 从左侧项

见证向量是 $[1, out, x, y, u, v, u1, u2]$。

矩阵 A 将成为如下形式：

A_{3,8} = 
\begin{pmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4} & a_{1,5} & a_{1,6} & a_{1,7} & a_{1,8} \\

a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8} \\

a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8} 
\end{pmatrix}

现在，让我们为第一行（第一个约束）填充矩阵 $A$。

$$u1 = x * y$$

由于左侧项中只有 $x$，因此 A 的第一行将为 $[0, 0, 1, 0, 0, 0, 0, 0]$。

因此，在第一个约束之后，我们得到

A_{3,8} = 
\begin{pmatrix}
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\

a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8} \\

a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8} 
\end{pmatrix}

现在，让我们为第二行（第二个约束）填充矩阵 $A$。

$$u2 = u * v$$

由于左侧项中有 $u$，我们将第二行的 A 设置为 $[0, 0, 0, 0, 1, 0, 0, 0]$。

因此，在第二个约束之后，我们得到

A_{3,8} = 
\begin{pmatrix}
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\

0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\

a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8} 
\end{pmatrix}

现在，让我们为第三行（第三个约束）填充矩阵 $A$。

$$out = u1 * u2$$

由于左侧项中有 $u1$，我们将第三行的 A 设置为 $[0, 0, 0, 0, 0, 0, 1, 0]$。

因此，在第三个约束之后，我们得到 $A$ 的最终形式。

A = 
\begin{array}{c}
\begin{matrix}
1&out & x & y & u & v & u1 & u2
\end{matrix}\\
\begin{bmatrix}
    0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 
\end{bmatrix}
\color{red}\begin{matrix}R_1\\R_2\\R_3\end{matrix}\hspace{-1em}\\
\end{array}

此处是表格形式的最终矩阵 A：

1 out x y u v u1 u2
R1 0 0 1 0 0 0 0 0
R2 0 0 0 0 1 0 0 0
R3 0 0 0 0 0 0 1 0

方法 2 R1CS 约束说明

另外，我们可以将三个约束中的左侧项表示为见证向量的线性组合。

$$u1 = x y$$ $$u2 = u v$$ $$out = u1 * u2$$

在这里，我们可以使用见证向量 $w$展开左侧项，并形成矩阵 $A$，如下所示。

$$u1 = (0.1 + 0.out + 1.x + 0.y + 0.u + 0.v + 0.u1 + 0.u2) y$$ $$u2 = (0.1 + 0.out + 0.x + 0.y + 1.u + 0.v + 0.u1 + 0.u2) v$$ $$out = (0.1 + 0.out + 0.x + 0.y + 0.u + 0.v + 1.u1 + 0.u2) * u2$$

因此，矩阵 $A$ 可以写为 

A = 
\begin{bmatrix}
    0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 
\end{bmatrix}

从右侧项构造矩阵 B

我们可以按照上述步骤进行，同样减少右侧项。

$$u1 = x (0.1 + 0.out + 0.x + 1.y + 0.u + 0.v + 0.u1 + 0.u2)$$ $$u2 = u (0.1 + 0.out + 0.x + 0.y + 0.u + 1.v + 0.u1 + 0.u2)$$ $$out = u1 * (0.1 + 0.out + 0.x + 0.y + 0.u + 0.v + 0.u1 + 1.u2)$$

因此，矩阵 $B$ 将如下所示：

B = 
\begin{bmatrix}
    0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 
\end{bmatrix}

从输出项构造矩阵 C

我们可以按照上述步骤进行，减少输出项。

$$(0.1 + 0.out + 0.x + 0.y + 0.u + 0.v + 1.u1 + 0.u2) = x y$$ $$(0.1 + 0.out + 0.x + 0.y + 0.u + 0.v + 0.u1 + 1.u2) = u v$$ $$(0.1 + 1.out + 0.x + 0.y + 0.u + 0.v + 0.u1 + 0.u2) = u1 * u2$$

因此，矩阵 $C$ 将如下所示：

C = 
\begin{bmatrix}
    0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
    0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
    0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 
\end{bmatrix}

Ex2 Sagemath 实现

我们可以通过以下 Sagemath 代码验证上述内容：


## 定义矩阵
A = matrix([[0,0,1,0,0,0,0,0],
            [0,0,0,0,1,0,0,0],
            [0,0,0,0,0,0,1,0]])

B = matrix([[0,0,0,1,0,0,0,0],
            [0,0,0,0,0,1,0,0],
            [0,0,0,0,0,0,0,1]])

C = matrix([[0,0,0,0,0,0,1,0],
            [0,0,0,0,0,0,0,1],
            [0,1,0,0,0,0,0,0]])

x = randint(1,100000)
y = randint(1,100000)
z = randint(1,100000)
u = randint(1,100000)

## 减法
out = x * y * z * u
v1 = x * y
v2 = z * u

## 见证向量
witness = vector([1, out, x, y, z, u, v1, v2])

## 计算结果
A_witness = A*witness
B_witness = B*witness
C_witness = C*witness
AB_witness = A_witness.pairwise_product(B_witness)

## 打印结果
print(f"A * witness = {A_witness}")
print(f"B * witness = {B_witness}")
print(f"C * witness = {C_witness}")
print(f"(A * witness) * (B * witness) = {AB_witness}")

## 检查等式
result = C_witness == AB_witness
print(f"result: ",result)

## 检查等式是否成立
assert result, "result contains an inequality"

输出将如下所示：

A * witness = (85530, 65887, 6198615690)
B * witness = (72473, 49454, 3258375698)
C * witness = (6198615690, 3258375698, 20197418725537501620)
(A * witness) * (B * witness) = (6198615690, 3258375698, 20197418725537501620)
result:  True

Ex2 Circom 电路实现

下面是此示例的 Circom 电路：

pragma circom 2.1.4;

template Multiply4() {
    signal input x;
    signal input y;
    signal input u;
    signal input v;

    signal u1;
    signal u2;

    signal out;

    u1 <== x * y;
    u2 <== u * v;   
    out <== u1 * u2;
}

component main = Multiply4();

/* INPUT = {
    "X": "5",
    "y": "10",
    "u": "3",
    "v": "4",
} */

让我们编译并生成见证。

circom multiply4.circom --r1cs --wasm --sym

snarkjs r1cs print multiply4.r1cs

cd multiply4_js

echo '{"x": "5", "y": "10", "u": "3", "v": "4"}' > input.json

node generate_witness.js multiply4.wasm input.json witness.wtns

snarkjs wtns export json witness.wtns witness.json

cat witness.json

我们得到以下输出。

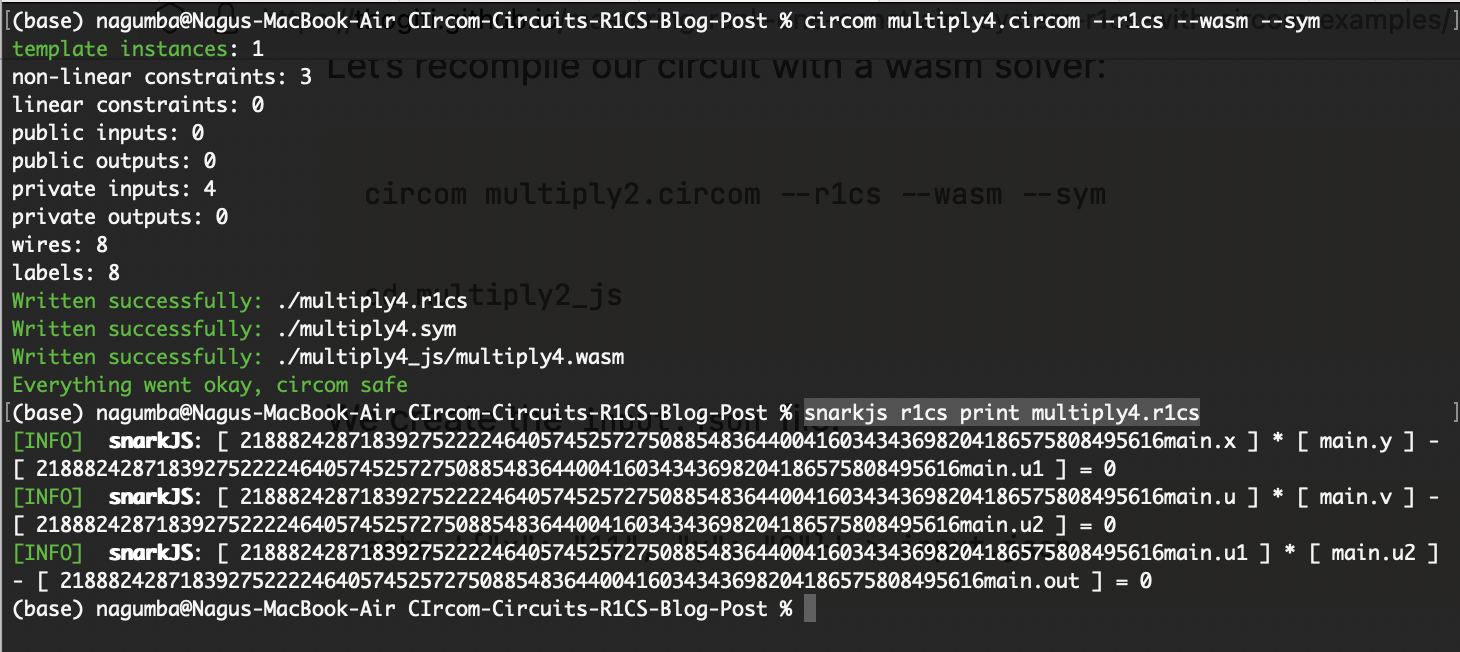
multiply4-r1cs-wasm-witness-output

在 multiplier4 电路中，我们采用了 x、y、u 和 v（4 根线）并将 u1 和 u2（+2 根线）与信号 out（+1 根线）连接，并检查了在 u1 <== x * y、u2 <== u * v 和 out <== u1 * u2 时的 3 个约束。因此，我们有 8 根线和 3 个约束。

示例 3

电路 $out = x*y + 2$

Ex3 R1CS 约束说明

我们可以重复上述归约过程，并获得矩阵。我们为 $out-2=x*y$ 写出矩阵。我们有一个约束，见证向量将是 $w = [1, out, x, y]$。

$A = [0, 0, 1, 0]$, $B = [0, 0, 0, 1], $C = [-2, 1, 0, 0]$

示例 4

电路 $out = 2x^2 + y$

Ex4 R1CS 约束说明

我们为 $out-y=2x^2$ 写出矩阵。我们有一个约束，见证向量将是 $w = [1, out, x, y]$。

$A = [0, 0, 2, 0]$, $B = [0, 0, 1, 0], $C = [0, 1, 0, -1]$

示例 5

电路 $out = 3x^2y + 5xy - x - 2y + 3$

Ex5 R1CS 约束说明

我们可以将方程归约为以下内容：

$$u1 = 3xx$$ $$u2 = u1*y$$ $$x+2y-3-u2+out = 5xy$$

我们有三个约束。我们的见证向量将是 $w = [1, out, x, y, u1, u2]$。

因此，矩阵 $A$、$B$ 和 $C$ 可以写为 

A = 
\begin{bmatrix}
    0 & 0 & 3 & 0 & 0 & 0  \\
    0 & 0 & 0 & 0 & 1 & 0  \\
    0 & 0 & 5 & 0 & 0 & 0 
\end{bmatrix}
B = 
\begin{bmatrix}
    0 & 0 & 1 & 0 & 0 & 0  \\
    0 & 0 & 0 & 1 & 1 & 0  \\
    0 & 0 & 0 & 1 & 0 & 0 
\end{bmatrix}
C = 
\begin{bmatrix}
    0 & 0 & 0 & 0 & 1 & 0  \\
    0 & 0 & 0 & 0 & 0 & 1  \\
    -3 & 1 & 1 & 2 & 0 & -1 
\end{bmatrix}

Ex5 Sagemath 实现

我们可以通过以下 Sagemath 代码检查这些矩阵：


## 定义矩阵

A = matrix([[0,0,3,0,0,0],
               [0,0,0,0,1,0],
               [0,0,1,0,0,0]])

B = matrix([[0,0,1,0,0,0],
               [0,0,0,1,0,0],
               [0,0,0,5,0,0]])

C = matrix([[0,0,0,0,1,0],
               [0,0,0,0,0,1],
               [-3,1,1,2,0,-1]])

x = randint(1,100000)
y = randint(1,100000)

## 减法
out = 3 * x * x * y + 5 * x * y - x- 2*y + 3
## 中间变量
u1 = 3*x*x
u2 = u1 * y

## 见证向量
witness = vector([1, out, x, y, u1, u2])

## 计算结果
A_witness = A*witness
B_witness = B*witness
C_witness = C*witness
AB_witness = A_witness.pairwise_product(B_witness)

## 打印结果
print(f"A * witness = {A_witness}")
print(f"B * witness = {B_witness}")
print(f"C * witness = {C_witness}")
print(f"(A * witness) * (B * witness) = {AB_witness}")

## 检查等式
result = C_witness == AB_witness
print(f"result: ",result)

## 检查等式是否成立
assert result, "result contains an inequality"

我们将看到输出：

A * witness = (133875, 5974171875, 44625)
B * witness = (44625, 61540, 307700)
C * witness = (5974171875, 367650537187500, 13731112500)
(A * witness) * (B * witness) = (5974171875, 367650537187500, 13731112500)
result:  True

Ex5 Circom 电路实现

以下是 Circom 电路：

pragma circom 2.1.4;

template Example5() {
    signal input x;
    signal input y;
    signal output out;

    signal u1;
    signal u2;

    u1 <== 3 * x * x;
    u2 <== u1 * y;
    out <== 5 * x * y + u2 - x - 2*y +3;
 }

component main = Example5();

/* INPUT = {
    "X": "5",
    "y": "10"
} */

让我们编译并生成见证。

circom Example5.circom --r1cs --wasm --sym

snarkjs r1cs print Example5.r1cs

cd Example5_js

echo '{"x": "5", "y": "10"}' > input.json

node generate_witness.js Example5.wasm input.json witness.wtns

snarkjs wtns export json witness.wtns witness.json

cat witness.json

我们得到以下输出。

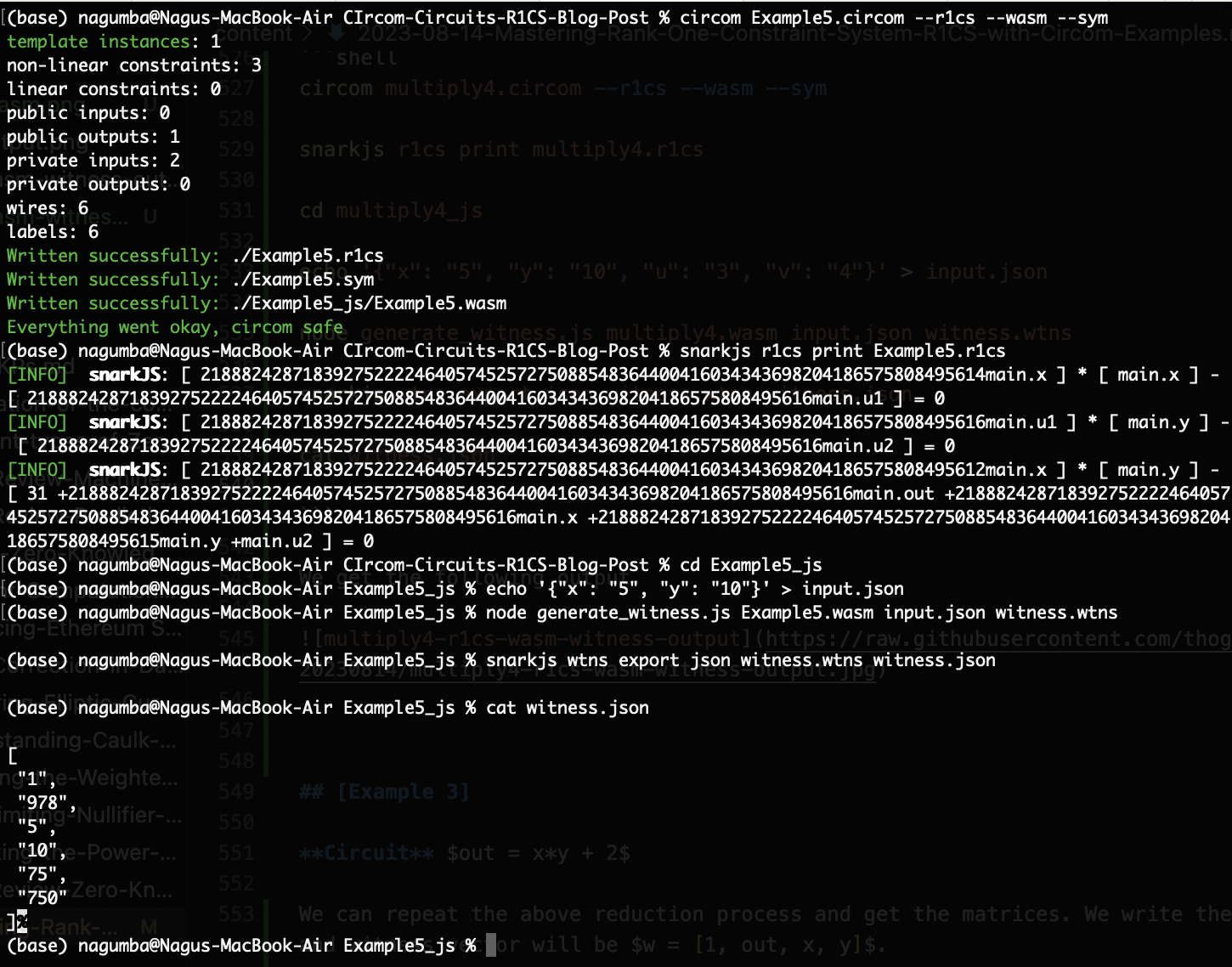
Example5-r1cs-wasm-witness-output

在 Example5 电路中，我们采用了 x 和 y（2 根线）并将u1 和 u2（+2 根线）与信号 out（+1 根线）连接，并检查了在 u1 <== 3 * x * x、u2 <== u1 * y 和 out <== 5 * x * y + u2 - x - 2*y +3 时的 3 个约束。因此，我们有 6 根线和 3 个约束。

注意 Circom 编译器默认只显示非线性约束（二次约束）。如果你想查看所有线性约束，可以使用 CLI 选项如下：

circom Example5.circom --r1cs --O0 --wasm --sym
  • 原文链接： github.com/thogiti/thogi...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
thogiti
thogiti
https://thogiti.github.io/

thogiti

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！