Tornado Cash是如何工作的？

介绍

Tornado Cash 是一个开源的去中心化币混合器，运行在以太坊网络上，由 Roman Semenov、Alexey Pertsev 和 Roman Storm 开发。它于 2019 年 12 月上线，截至 2024 年 3 月，已有 400 万 ETH 存入，池中有 12.5 万 ETH（ Tornado Cash 分析↗）。Tornado Cash 提供的功能是一把双刃剑：它提供强大的匿名性，使以太坊联合创始人 Vitalik Buterin 能够 向乌克兰发送匿名资金↗，但它也允许通过犯罪活动获得的币被洗钱。例如，朝鲜政府黑客团伙Lazarus↗和Euler金融黑客都使用 Tornado Cash 混合了他们的币。

在这篇文章中，我们将讨论 Tornado Cash 背后的数学原理。让我们深入研究 Tornado Cash！

警告: 截至 2022 年 8 月，美国财政部外汇办公室已宣布 在 美国或与美国人士有关的任何涉及 Tornado Cash 的交易都是 被禁止的。本文仅用于教育目的。我们对信息的任何误用不承担责任。

背景

哈希函数

哈希函数 是一种数学函数，接受任意大小的输入消息，并返回一个称为哈希值的固定大小字符串。例如，$f(x)=x%97$ (将 $x$ 除以 97 的余数) 是一个适用于整数输入的哈希函数。哈希函数的目的是生成输入数据的唯一数字指纹，可以用于多种目的，例如数据存储、数据检索、数据完整性检查、数字签名和密码验证。

我们可以定义一种特殊类型的哈希函数，称为 加密哈希函数。如果哈希函数 f 满足以下三个安全属性，则称其为加密哈希函数：

1. 抗原像性：给定哈希值 h，找到任何输入消息 m 是困难的，使得 $f(m)=h$。
2. 抗第二原像性：给定输入消息 m，找到消息 $m'（≠m）$使得$ f(m')=f(m)$ 是困难的。
3. 抗碰撞性：找到任何两个不同的输入消息 m1, m2（≠m1）使得 f(m1)=f(m2) 是困难的。

有许多不同的哈希函数可用，每个都有其自身的特性、优点和缺点。常见的哈希函数包括 MD5、SHA-1、SHA-2 和 SHA-3。（注意：MD5 和 SHA-1 现在已经被弃用，通常不应该用于加密目的。）

Merkle 树

Merkle 树 是一种树数据结构，广泛用于密码学和计算机科学，以有效验证大量数据的完整性和真实性。其结构基于加密哈希函数。要构造 Merkle 树，首先对要存储的元素进行哈希处理，并将生成的哈希值安排为树的叶节点。然后，相邻的叶节点成对哈希以创建一组新的哈希值，作为前一个叶节点的父节点。这个过程递归重复，直到生成一个被称为根哈希的单一哈希值。以下是将元素 “Alice”、 “Bob”、 “Charles”、 “Daniel”、 “Emma”、 “Fiona”、 “Grace”、 和 “Henry” 存储在 Merkle 树中的示例。

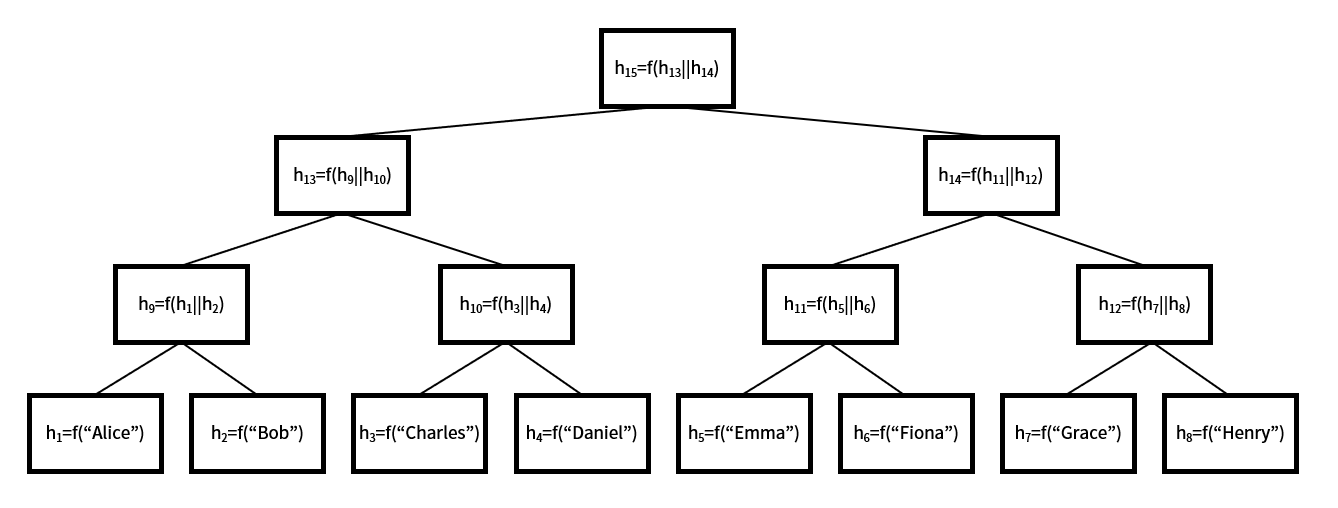
将元素 “Alice”、“ Bob”、“ Charles”、“ Daniel”、“ Emma”、“ Fiona”、“ Grace”、 和 “Henry” 存储在 Merkle 树中的示例；f 是一个加密哈希函数。

在将元素存储在此 Merkle 树之后，根 h_15 被打开。为了证明 “Alice” 在 Merkle 树中，只需提供 h2, h_10, h_14。然后验证者可以通过 $h_15=f(f(f(f("Alice"),h2),h_10),h_14)$ 重新计算 h_15。这一额外的值被称为 Merkle 证明 (也称为 Merkle 路径)。

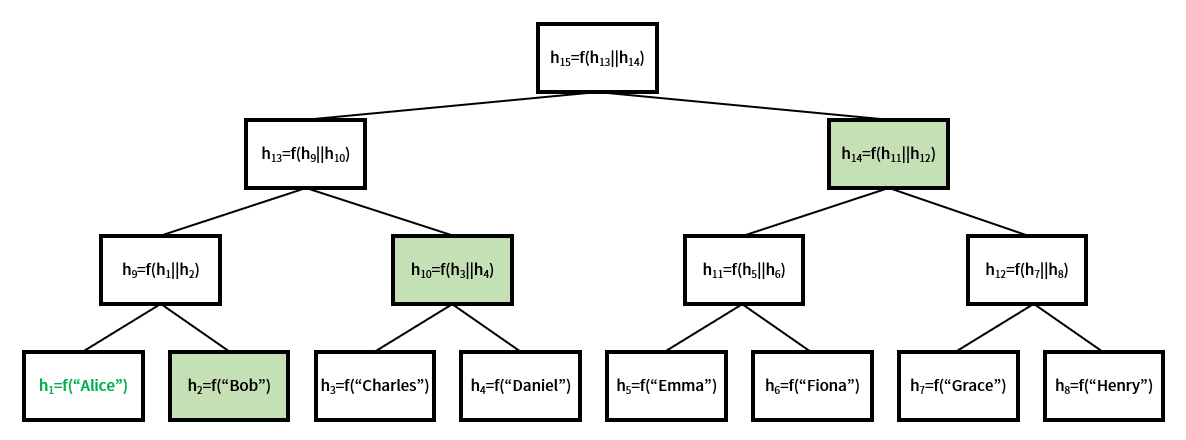
证明元素 “Alice” 在 Merkle 树中存在的示例。绿色的框表示 Merkle 证明。

由于 f 的抗原像性，Merkle 证明不会泄露其他存储的元素，并且在 Merkle 证明中的元素总数是存储在 Merkle 树中的元素总数的对数规模。

承诺方案

承诺方案 是一种加密协议，允许一方承诺某个消息或值，而不揭示该值本身，并在之后以可验证的方式公开。这在一方需要证明他们在早期时间对某个特定消息做出了承诺的场景中很有用，而无需在稍后的时间暴露该消息。看看这个场景：

Alice 已知道明天纳斯达克的收盘价 p。 Alice 想要 在不揭示该 值本身的情况下 说服他人其前知。为了做到这一点，Alice 可以通过选择足够长的随机字符串 secret 并公开 $com=f(secret∥∥p)$，以承诺价格 p，其中 f 是一个加密哈希函数，∥∥是连接操作。由于抗原像性属性，无法通过 com 恢复 p。明天，p 对所有人都是已知的。然后，Alice 打开 secret。现在 Alice 的前知通过检查 $com \overset ? {=} f(secret∥∥p）$来验证。

信息 问题：secret 是否必要？如果将 $com=f(p)$ 而不是 $ com=f(secret∥∥p) $ 定义会怎样？ 答案：p 可以通过检查 f(1),f(2),…来揭示，直到哈希值与 com 一致。secret 作为盐可以防止通过暴力破解哈希以揭示 secret。

(非交互式)零知识证明

零知识证明 是一种加密协议，允许证明者向验证者展示特定陈述为真，而不泄露超出该陈述本身真相的任何其他信息。换句话说，它允许证明者说服验证者他们知道一个秘密值，而不公开该值或关于它的任何其他信息。零知识证明必须满足以下三个属性：

1. 完整性(Completeness)：如果陈述为真，则诚实的证明者应该能够说服验证者其真。
2. 可靠性(Soundness)：如果陈述为假，则无欺骗性的证明者不能说服验证者其真。
3. 零知识性：证明不应泄露超出陈述真实情况的任何额外信息。

附加说明

完整性和可靠性是明确的，但零知识性对于初学者来说可能会令人困惑。我们能否正式定义“没有向验证者透露任何额外的信息”？答案是 是的。为了证明给定协议的零知识性，我们展示证明者与验证者之间传递的每条消息都可以被不认识该陈述的人模拟。对我来说，图着色问题的零知识证明能很好地帮助理解零知识证明的概念。建议查看 这篇文章↗。

零知识证明分为两种类型：交互式 或 非交互式，取决于证明者与验证者之间的通信。如果证明者和验证者通过交换消息进行互动，类似于口头考试，则该协议称为交互式。另一方面，如果证明者生成一个可以在无需进一步交互的情况下被验证者验证的证明，该协议称为非交互式。

还有几个示例的零知识证明协议，例如 zk-SNARK、zk-STARK、Bulletproofs 和 Ligero。虽然本文只介绍了稍后将在 Tornado Cash 中使用的 zk-SNARK 的细节，但最重要的事情是，对于任何函数 f 和给定的输出 y，可以证明某个输入 x 满足 f(x)=y，而不揭示 x。此外，任何交互式零知识证明都可以转化为非交互式零知识证明。最后，对于任何函数 f 和给定输出 y，证明者仅通过发送证明 π 给证明者 而不需要交互，来证明他们 对某个输入 x 满足 f(x)=y 的知识，而不揭示 x。

协议概述

Tornado Cash 的目标是通过允许用户进行私人交易来为他们提供完全的匿名性。因此，Tornado Cash 的主要功能仅为存款和取款。用户可以通过一次交易以预定的以太币金额进行存款和取款。具体金额在 白皮书↗ 中并未规定，但在当前实现中为 0.1 或 1 或 10 或 100 ETH。固定金额的原因是为了防止根据其价值追踪交易。例如，有来自 addrin_1, addrout_2,…, addrout_10 的 10 笔存款和来自 addrout_1, addrout_2,…, addrout_10 的 10 笔取款。如果每笔存款的金额不同，链接存款地址和取款地址将变得非常简单。

设置

首先，Tornado Cash 使用 Pedersen 哈希函数↗ 和 MiMC 哈希函数↗。我们分别将这两个函数表示为 H1 和 H2。合约有一个高度为 20 的 Merkle 树，其中每个非叶节点是其两个子节点使用 H2 的哈希。由于高度为 20，该树有 $2^20$ 个叶子。叶子最初初始化为 0，当进行存款时，从左到右将以某个值替换这些叶子。由于每个叶子对应单个存款，因此合约仅支持 $2^20$ 次存款。在 $2^20$ 次存款后，将不再允许更多存款。

附加说明

当合约维护 Merkle 树时，并不需要在树中存储所有的叶子。只需存储每个 "新使用" 叶子对应于从最近插入的叶子到根的路由节点的 20 个元素即可。如需更多详细信息，请查看 代码↗。filledSubtrees 是表示上述 Merkle 树的数组。

虽然不是必要的，合约存储最近 n=100（如白皮书中提到的）或 30（在实现中）的根值以方便用户，而不仅仅是最新的一个。最后，合约还有一个用于防止双重支出的空值哈希列表，稍后我们将介绍。

存款

存款过程如下：

1. 用户生成两个随机数 k (nullifier) 和 r (secret)，并计算承诺 $C=H_1(k∥∥r)$。这两个数字必须被 记住。这就是我们在文章开头介绍的承诺方案。
2. 向合约发送包含数据 C 的 ETH 交易。如果树没有满，合约接受交易并用 C 替换最左边的零叶。这样树中的 20 个元素将发生变化，包括根。

请注意，k 和 r 是隐藏的，但承诺 C 是公开的，每次存款的顺序也得以保留。例如，最开始，如果地址 0x111、0x222 和 0x333 进行存款，那么公众知道第一个叶子属于 0x111，第二个叶子属于 0x222，第三个叶子属于 0x333。然而，这几乎不意味着什么，因为在取款时不会透露叶子索引。

取款

取款过程如下：

1. 计算 Merkle 证明 O，证明 C 在根 R 的 Merkle 树中存在。根 R 必须是最近 n 个根值之一。
2. 计算空值哈希 $h=H_1(k)$。
3. 计算证明 π，证明 l, k, r 的知识，使得 $h=H_1(k)$ 且 O 是第 l 个叶子 $C=H_1(k∥∥r)$ 的有效 Merkle 证明。
4. 向合约发送包含 R, h, π 的 ETH 交易。如果证明 π 有效且 h 不在空值哈希列表中，则合约接受请求。
5. 合约将 h 添加到空值哈希列表中。

要理解此取款程序，我们回顾非交互式零知识证明 (NIZK)。在 NIZK 中，证明者可以通过仅向证明者发送证明 π，而不需要交互，来证明他们 对某个输入 x 满足 f(x)=y 的知识。

一旦我们将 f 定义为

$$ f(l, k, r, O) = \begin{cases} 1, & \text{if } h = H_1(k) \text{ and } O \text{ is valid Merkle proof for } l \text{-th leaf} \ 0, & \text{else} \end{cases} $$

并将目标输出设为 y=1，那么证明 π 代表证明者是合法的取款者 而不揭示 l, k, r, O，从而保证了匿名性。我们会在 "Tornado Cash 中的零知识证明" 部分进一步讨论证明内容。

取款程序似乎是合理的。但是费用怎么办？如果用户想将币取款到一个新钱包，钱包没有余额无法支付费用。同时，从原钱包支付也是不可能的，因为这将允许将新钱包与原钱包关联，违反匿名性。为了解决这个问题，用户可以选择使用 中继。用户选择币接收地址 A 和费用 f，并将其包含在证明 π 中。然后用户将证明发送给中继，中继将其传输到合约。中继商以收入为补偿，但他们不能更改任何取款数据，包括接收地址。

Tornado Cash 中的零知识证明

现在我们对 Tornado Cash 有了一个总体的了解。在本节中，我们将更深入地探讨 Tornado Cash 中使用的零知识证明。

zk-SNARK

推荐 zk-SNARK 背后的数学，如群论、椭圆曲线、配对和 sigma 协议相当具有挑战性。虽然我们将在本节中提供 zk-SNARK 的简要介绍，但对于第一次接触该概念的人来说，这可能不够。幸运的是，网上有很多文章和幻灯片介绍 zk-SNARK 和它们的基本概念。如果你是新手，我们建议你先阅读这些资源，以便更好地理解。

zk-SNARK 是 零知识简洁 非交互式知识参数的缩写。

1. 零知识：验证者无法知道除了陈述为真的其他任何信息。
2. 简洁：证明大小和验证时间是 子线性的。
3. 非交互式：无需交互。
4. 知识参数：不仅是对输入 x 的存在，还包括证明者对 x 的知识。

不仅零知识，而且简洁性也是神秘的。例如，如果证明者想证明他们对输入 x 的知识，使得 $SHA256(x)=0^{256}$，除了零知识性，最简单的方法就是将 x 发送到验证者。当然，证明的大小是 ∥x∥ 而验证者的时间与计算 SHA256(x) 完全相同，所以这并不简洁。现在我们面临的问题是， 是否有可能以比 直接计算 更低的成本证明某些事情_？在我们介绍 zk-SNARK 的细节之前，我们将展示一个简单的示例，允许验证者接受的证明所需的计算量少于直接计算。这是该示例：

有两个 n×n 矩阵 A，B，C。证明者想证明 C=AB（C = A \times B）。如果验证者直接计算 AB 并与 C 进行比较，时间复杂度是 $O(n^3)$——或通过使用一个 先进算法↗ 来获取 $O(n^{2.373})$。然而，如果验证者选择大小为 n 的随机向量 v，检查 A⋅(Bv) 是否等于 Cv，其时间复杂度降至 $O(n^2)$。即使存在 $AB≠C$，但 $A⋅(B_v) \overset ? {=} C_v$，验证者仍可能接受错误的 C，但当验证者针对不同的 v 重复此验证时，此类情况的概率会显著降低。

Groth16

接下来，处理 Tornado Cash 的实际使用的零知识证明系统。Tornado Cash 使用 Groth16↗，这是 Pinocchio↗ 的改进版本。在 Groth16 中，证明者将其陈述转化为 QAP（二次算术程序）形式。我们将利用简单的示例逐步展示转化过程：

def f(x, y):
    return x**2 + 3 * y**2 + 10

assert f(x,y) == 17 # f(2, 1) = 17

扁平化

证明者希望证明他们对 x,y 满足 f(x,y)=17 的知识。为此，证明者首先将给定陈述转换为一系列特殊形式，其中 x = y 和 x = y (op) z，其中 y, z 可以是变量或数字，且 op 可以是 + 或 *。这类似于编译器中的三地址代码。方程 f(x,y) 的转换如下：

x2 = x * x
y2 = y * y
t1 = 3 * y2
t2 = x2 + t1
out = t2 + 10

R1CS

扁平化后，这些条件被转换为 R1CS（Rank-1 Constraint System）。R1CS 是一个方程系统，每个方程由一个三元组向量定义

$(a⃗ _i,b⃗ _i,c⃗ _i) $满足$ (a⃗ _i⋅s⃗)×(b⃗ _i⋅s⃗)=(c⃗ _i⋅s⃗)。$在我们的示例中，我们将构建这样一个系统，使解向量 $s⃗=(1,x,y,x2,y2,t1,t2,out)$。举例来说，扁平化方程 $x2=x * x$ 被转换为：

$$ \begin{align} \vec{a}{-1} &= (0, 1, 0, 0, 0, 0, 0, 0) \ \vec{b}{-1} &= (0, 1, 0, 0, 0, 0, 0, 0) \ \vec{c}_{-1} &= (0, 0, 0, 1, 0, 0, 0, 0), \end{align} $$

正如你所见，这些向量$ (a⃗ _i,b⃗ _i,c⃗ _i)$ 中的每一个元素代表在方程系统中用于变量（或常数）的系数。而解向量 $s⃗ $ 表示在该系统中使用的所有变量。

继续我们的示例，y2 = y * y 被转换为：

$$ \begin{align} \vec{a}_2 = (0,0,1,0,0,0,0,0) \ \vec{b}_2 = (0,0,1,0,0,0,0,0) \ \vec{c}_2 = (0,0,0,0,1,0,0,0) \ \end{align} $$

t1 = 3 * y2 被转换为：

$$ \begin{align} \vec{a}_3 = (0,0,0,0,1,0,0,0) \ \vec{b}_3 = (3,0,0,0,0,0,0,0) \ \vec{c}_3 = (0,0,0,0,0,1,0,0) \ \end{align} $$

而 t2 = x2 + t1, out = t2 + 10 被转换为：

$$ \begin{align} \vec{a}_4 = (10,0,0,1,0,1,0,0) \ \vec{b}_4 = (1,0,0,0,0,0,0,0) \ \vec{c}_4 = (0,0,0,0,0,0,0,1) \ \end{align} $$

在这个格式中表示所有扁平化方程后，只有知道正确 x,y 的证明者能够找到给定约束系统的解向量 $ s⃗。$ 因此，证明者的最终目标是证明他们知道$ s⃗。$

QAP

QAP 的目的在于证明同一系统，但使用多项式而不是向量点积来减少通信成本。根据 R1CS 中的向量，可以推导出多项式。例如，多项式 a1 是通过以下点定义的

$a1(1)=0,a1(2)=0,a1(3)=0,a1(4)=10$，其中 0,0,0,100 对应解向量中元素的相关项。这是一个 3 次多项式，可以通过 拉格朗日插值法↗ 生成。而 $a_x, ay, a{x2}, a{y2}, a{t1}, a{t2}, a{out}$ 也以相同方式生成。对于 $b1, ..., b{out}, c1, ..., c{out}$ 也是如此。

设 $\vec{A}=(a1,ax,a_y,a_x2,ay2,a{t1},a{t2},a{out})$ (是的，多项式向量，同样 $ \vec{B}, \vec{C}$ 也是这样）。显然，$(\vec{A}=(x)⋅\vec{s})⋅(\vec{B}(x)⋅\vec{s})= \vec{C}(x)⋅\vec{s}$。对于 x=1,…,4，设 $ A(x) = (\vec{A}(x)⋅\vec{s}) $ 同样 $ {B}, {C}$ 也是这样，则有多项式 $H(x)$，使得 $A(x)⋅B(x)−C(x)=H(x)⋅(x−1)(x−2)(x−3)(x−4)$。 如果正确选择 $\vec{s}$，这个过程能够在例子中成立 $f(2,1)=17$，因此 $\vec{s} = (1, 2, 1, 4, 1, 3, 7, 17)$ 这个 $\vec{s}$ 被称为 满足的赋值。

在这段长旅程之后，我们将陈述转化为多项式的乘法。如果证明者能够证明...

1. A(x), B(x) 和 C(x) 是从同一个 $\vec{s}$ 派生的，并且
2. 存在 H(x) 使得 $ A(x)⋅B(x)−C(x)=H(x)⋅Z(x) $ 其中 $Z(x)=(x−1)(x−2)(x−3)(x−4) $，

然后验证者接受证明者的知识。为了保证 简洁性，而不是直接处理多项式，检查某个随机点 $t$ 的 $A(t)⋅B(t)−C(t)=H(t)⋅Z(t)$。

同态隐藏与配对

等式 $ A(t)⋅B(t)−C(t)=H(t)⋅Z(t) $ 可以成立于某个 $t$ 当 $ A(x)⋅B(x)−C(x)≠H(x)⋅Z(x) $。这个概率是可以忽略的，但如果 $t$ 是已知的，那么攻击者可以轻易地构造 $A(x), B(x), C(x), H(x)$满足 $A(t)⋅B(t)−C(t)=H(t)⋅Z(t) $ 。因此 $t$ 应该被隐藏，但允许证明者计算$ A(t), B(t), C(t), H(t)$。这似乎是矛盾的，但 同态隐藏 允许这样做。根据椭圆曲线离散对数问题的困难性，我们定义一个加密函数 $E(x)=xg $ 对于一个生成元 $g$。然后 $E$ 满足以下条件：

1. 从 $E(x)$ 中找到 $x$ 是困难的。
2. $x≠yx $， 则 $E(x)≠E(y) $。
3. $E(x+y)=E(x)+E(y)$。
4. $a⋅E(x)=E(ax) $。

而不是直接给 $t$ 给证明者，证明者获得的是 $E(t^0), E(t^1), \dots $ 然后，由于$ A(t), B(t), C(t) $, 和 $H(t)$ 是 $t^0, t^1,…$ 的线性组合，证明者可以计算 $E(A(t)), E(B(t)), E(C(t)), E(H(t)) $。而且，$ E(A(t)), E(B(t)), E(C(t)), E(H(t)) $ 实际上源自$ E(t^0), E(t^1), \dots $ 可以通过 系数知识假设 测试 来证明。我们在本文中省略了系数假设测试的信息。

现在证明者生成$E(A(t)), E(B(t)), E(C(t)), E(H(t)) $，这些将被传递给验证者，验证者可以生成 $E(Z(t))$ 因为 $Z(x)$是已知的。然而，验证者不能检查 $A(t)⋅B(t)−C(t)=H(t)⋅Z(t) $ 因为 $E$ 在乘法中不是同态的。我们需要另一种映射称为 配对↗。 配对是一个映射 $e : G_1 \times G_2 \rightarrow G_T$，满足 $e(aP,bQ)=ab \cdot e(P,Q)$ 其中 $G_1, G_2$ 是具有相同方程但不同生成元 $g_1, g_2$的椭圆曲线，顺序为 $q$，$G_T$ 是一个顺序为 $q$ 的循环群。我们稍微扩展 $E$ 到 $E_1$ 和 $E_2$，其中 $ E_1(x) = xg_1, E_2(x) = xg_2$ 。

从现在开始，我们可以相乘隐藏值。最后，检查 $A(t)⋅B(t)−C(t)=H(t)⋅Z(t) $ 是从 $ e(E_1(A(t)), E_2(B(t)) / e(E_1(C(t)), E_2(1)) \stackrel{?}{=} e(E_1(H(t)) cdot E_2(Z(t))) $。 由于仅需要 $ E_1(A(t)), E_2(B(t)), E_1(C(t)) $来验证，证明大小固定为 $2$ 个 $ G_1 $ 元素和 $1$ 个$G_2$元素。

可信设置

在此过程中，证明者需要 $E_1(t^0), E_1(t^1), … ,E_2(t^0),E_2(t^1),… $通过一个随机的 $t$ 生成。一个可能的场景是验证者选择随机的 $t$，生成 $E_1(t^0), E_1(t^1), \dots,E_2(t^0),E_2(t^1), \dots $并将这些值发送给证明者。然而，这种方法对证明者非常耗费成本，仅能实现交互式模型。在非交互式模型中，验证者不能向证明者发送任何东西。因此，代替验证者，第三方生成 公共参考字符串 (CRS) **** $ E_1(t^0), E_1(t^1), \dots,E_2(t^0),E_2(t^1), \dots $并向所有人公开。这称为 可信设置。可信设置的要求是 zk-SNARK 的显著弱点。

附加说明 最初，CRS 包含除了 $E_1(t^i), E_2(t^i)$ 以外的一些电路特定值，确切的过程稍微复杂，因为它需要检查$ A(x), B(x), $以及 $C(x)$是否是使用系数知识假设的知识派生于同一个 $ \vec{s}$。你可以参考 Groth16 论文↗ 以了解更多有关此主题的信息。

power-of-tau

在 Tornado Cash 中，用户充当证明者，而合约作为验证者。在 Tornado Cash 的测试版中，Tornado Cash 团队生成了 CRS 并使其公开（ 请参见 此处↗，证明密钥和验证密钥是从 CRS 派生的）。如果所有用户信任 Tornado Cash 团队，他们可以使用该团队提供的 CRS 生成证明。然而，如果 Tornado Cash 团队变得恶意，他们可能会生成伪造的证明，并可能窃取所有币。为了解决这个问题，Tornado Cash 团队更换了来自加密社区生成的 CRS，称为 power-of-tau。用户 $1$ 到 $k$ 首先持有自己的随机 $t_1, t_2, \dots, t_k$。用户 $1$ 生成 $E_1(t_1^0), E_1(t_1^1), \dots,E_2(t_1^0),E_2(t_1^1), \dots $。注意 $E_1(t_1^i) = t_1^i \cdot g_1, E_2(t_1^i) = t_1^i \cdot g_2 $。然后用户 $2$ 生成 $E_1((t_1t_2)^0),E_1((t_1t_2)^1), \dots,E_2((t_1t_2)^0),E_2((t_1t_2)^1), \dots $、从 $E_1((t_1t_2)^i) = t_2^i \cdot E_1(t_1^i), E_2((t_1t_2)^i) = t_2^i \cdot E_2(t_1^i) $，未知道 $t_1$。在用户 $k$ 生成完这个列表后，公共参考字符串 CRS 由秘密 $t = t_1t_2 \dots t_k$生成。在 Tornado Cash 的情况下， 1,114 用户参与↗ 且 CRS 已成功替换↗。

在 Tornado Cash 中的实现

现在我们回到 Tornado Cash 中的声明。我们的目标是证明和 验证 $l,k,r,O$ 的知识，使得$ f(l,k,r,O)=1$

$$ f(l, k, r, O) = \begin{cases} 1, & \text{if } h = H_1(k) \text{ and } O \text{ is valid Merkle proof for } l \text{-th leaf} \ 0, & \text{else} \end{cases} $$

这个 fff 需要被转化为 QAP。Tornado Cash 使用电路编译器 Circom↗ 和snarkjs↗。电路编译器 Circom 有它们自己的语言 circom 语言↗。在用 circom 语言↗ 编写完 fff 之后，代码被转化为 R1CS，随后 snarkjs 几乎处理一切，比如生成 CRS（在 Tornado Cash 的情况下通过可信设置仪式）、证明和 智能合约用于验证↗。

安全问题

在这一节中，我们将讨论一些协议和用户级别的安全问题。必须注意，解决这些问题并不一定意味着 Tornado Cash 是脆弱的。

哈希函数

使用不同的哈希函数 $H_1$ 和 $H_2$ 似乎是不必要的，作者没有给出这个选择的理由。审计 Tornado Cash 的 ABDK 咨询公司也指出了这一点 (请参见这里， 第 5.1 节)↗。 此外，Pedersen 哈希函数具有同态性质，因此它不是一种密码学哈希函数。相反，将 $H_1$ 和 $H_2$ 都定义为 MiMC（或任何其他适合 SNARK 的哈希函数）并施加域分离可能会更好。

依赖性

合约源代码并不长且分析良好。然而，通常情况是，小缺陷可能造成这一领域的灾难。事实上，在 2019 年 10 月，Tornado Cash 团队发现一个漏洞，攻击者可以由于 zk-SNARK 实现 MiMC 的外部依赖性问题进行任意存款 (请参见这里)↗。因此，所有依赖也必须仔细审核。

用户错误

用户必须选择高熵的 $k$ 和 $r$。用户错误也可能导致失去匿名性。我们建议你阅读 这篇 文章↗。

结论

Tornado Cash 是一个流行的去中心化币混合器，在以太坊网络上通过使用密码学技术为用户提供强大的匿名性。作为 Tornado Cash 的一大特点就是进行私密交易的匿名性，我们查看了它们存款和取款背后的数学。在对其零知识证明系统 Groth16 进行深入研究后，我们举例说明了如何通过引用扁平化、同态隐藏和配对等变换证明者的声明为二次算术程序形式，以及 R1CS，之后讨论了一些程序，如可信设置和次方 - 幸运。还需要注意几个安全问题（包括使用不同的哈希函数、需审计的依赖性和用户错误）。由于 Tornado Cash 中的匿名性和隐私性是其最强大的特点之一，因此很有趣地看看其背后的数学。

免责声明 值得注意的是，虽然 Tornado Cash 提供的匿名性可能是有益的，但它也可以用于非法或被禁止的活动。此外，再次强调，在美国或美国人之间进行任何交易使用 Tornado Cash 是被禁止的。我们建议你自行进行研究，并在与 Tornado Cash 交互之前咨询合格的法律顾问。

• 原文链接： zellic.io/blog/how-does-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～