深入探讨椭圆曲线（第5部分）

在我们之前的交流中，我提到过几次椭圆曲线的群运算（点加法）感觉有点……强行。或者说，用_复杂_作为更合适的描述。

就像某个智力超群的人用200年的数学知识为了某种我们简单凡人无法理解的神秘原因设计了这样的方式。

到现在为止，我们至少有了一些关于为什么椭圆曲线可能是一种有趣群体的概念。我们看到了可以用它们做一些很酷而特别的事情——例如，如何产生曲线的扭曲。这些行为赋予椭圆曲线特殊的特性，而其他群体可能不会表现出来。

然而，我们仍然有一个挥之不去的问题：到底是谁 想出了这个奇怪的点加法策略？而为什么？我们难道可以有不同的做法吗？

好吧，今天我们将回答这些问题。但我们需要的工具是_相当抽象_的。

如果你明白了，那就明白了。

因为今天，我们终于要谈谈因子。

这不仅会让我们更好地理解点加法操作，还会为我们定义和理解_配对_铺平道路。

废话不多说，赶紧开始吧！

因子

这没什么好掩饰的。我会直接给你实际的定义。以下是：

在任何带有代数闭包 K̄ 的域 K 上的曲线 C 上，因子是一种表达曲线上点的集合 的方式，写成和的形式：

其中 nₚ 是在有限多个点上非零的整数。

天哪

我警告过你们的！

让我们试着对此进行一些解释。

首先，我们看到因子_并不局限于_椭圆曲线。它们也并不局限于_整数模 p 的域。它们是一种更通用的工具，并且在理解其他类型的系统时有应用。

其次，我们从未定义过什么是一个域的代数闭包。事实上，考虑到我们的目的，我们不需要太担心这一点。但为了完整性，我们快速解释一下。

一个域 K 的代数闭包与具有系数在 K 的多项式的可能解有关。在这里，考虑一个熟悉的域：实数。

多项式 P(x) = x² + 1 没有 实数解。这就是说，某些解是不在我们原始域上的。代数闭包包括所有具有实系数的多项式的所有可能解——实际上，实数的代数闭包是复数！

在椭圆曲线的上下文中，处理有限域的闭包仅有一个目的：将无穷远点 (𝒪) 引入混合体。

我们关心的就是这个——长话短说。我们唯一关心的是，在椭圆曲线的上下文中，C 只是一个这样的曲线 E，而 K=𝔽ₚ。代数闭包使我们能够将无穷远点作为可能的多项式解。故事到此结束。

我接受这个。

好吧，回到因子。这里是公式：

定义提到这是一个点的集合——实际上是一个_多重集合_的点。这个多重性由 nₚ 表达。想象一下，如果点 P 在这个集合中出现了“三次”，我们就有 nₚ = 3。但这种表示的有趣之处在于 nₚ 可以是负值。

最后，定义说道，除了_有限多个_外，所有 nₚ 系数均为零。换句话说，这只是在说和是_有限_的。

总的来说，因子可能看起来像这样：

值得注意的是，这不是将点相加。3(P) 和 [3]P 并不相同，后者意味着将 P 加三次。而这一整个表达式的结果不是一个点！它是一个因子。

事情开始得有点疯狂，但我们已经掌握了一些基础。一切都好。

不清楚的是我们为什么关心这些东西。

因子和函数

因子与函数和曲线的_交点_有着紧密的关系。它们还很好地编码了这些点的多重性。

例如，考虑一条与椭圆曲线相交的直线。我们已经知道它的行为——我们将得到三个交点。这些点将是 P、Q 和 -(P+Q)。

也许更令人惊讶的是，这条直线也“相交”𝒪。其原因在查看项目坐标时会显现：

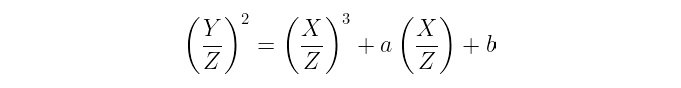
我们可以看到，在 Z = 0 处有一个极点（或奇点，或者说是函数_趋向无穷大的点），并且 Z 出现了三次。置信不会意外的是，𝒪 的_多重性_为3。

总的来说，直线 𝓁 的因子为：

如果你思考一下，我们在这里得到了一个_根_和_极_的表示，这些都是通过将 𝓁 代入 E 得到的。我们可以看到，根是有正的多重性，而极是有负的多重性。

一般来说，函数 f 的因子 定义为：

其中 ordₚ(f) 代表点 P 的多重性。

因子的另一个有趣之处在于我们可以将它们相加。而且，还有一个非常有用的代数翻译，将函数转换为它们的因子：

这开始看起来可能不是很激动人心。但是，想一想：仅仅通过加减因子，就能得知关于函数与曲线的_商_或_积_的交点的一些信息。这是很强大的，因为我们甚至可能不知道那些商或积的形状。很快这将派上用场。

因子和群体

接下来有一系列定义，将带我们探索因子的群结构。

我敢打赌你没想到这一点！

事情会变得有点棘手。让我们慢慢来。

曲线上的因子

当然，椭圆曲线（好吧，实际上任何曲线）有许多因子。在实数域上，它有无限多个。但在有限域上，曲线的因子集合变成有限的。

我们将曲线 E 的所有因子集合表示为 Div(E)。

我们也应该指定该域的代数闭包作为下标，但为了简单起见，我们可以忽略它。而且，我实在无法用unicode字符书写它！

因为我们可以相当自然地将因子相加——但我们_不能相乘_它们——所以曲线上的所有因子构成一个群体。规则很简单。加法像你所期望的那样工作：

而该群的_单位元_是零因子：一个每个 nₚ 为零的因子。

现在是时候介绍几...