椭圆曲线深入解析（第二部分）

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～

上一次，我们定义了椭圆曲线是什么，并 devised 了一种（可疑复杂的）方法来将曲线上的点相加。我们也暗示了这种操作对密码学应用的重要性。

然而，定义在实数上的曲线并不是我们所追求的构造。

密码学是一门离散精度的学科。我们希望算法能够产生一致、可重复的结果。换句话说，我们追求的是确定性，这粗略地说意味着使用相同的输入应该得到相同的输出，无论是什么情况。

在这个意义上，处理实数是相当麻烦的，因为我们通常使用浮点运算，因此总是存在舍入误差，使得操作不精确。

由于舍入误差，添加 P ⨁ Q 的结果甚至可能完全不落在曲线上（在实数上工作时）。

这需要采取不同的策略。

这将是我们今天的起点！我们将先进行一个小小的绕路，然后直接回到椭圆曲线上。

合适的领域

与实数相对，整数在操作上非常精确。因为没有小数，所以舍入误差似乎不再是问题！

尽管这对加法、减法和乘法是正确的，但看起来除法可能会有一些问题：1 除以 3 显然不会得到一个整数，我们又回到了浮点运算的领域。

我们还需要问自己，我们可以允许我们的整数有多大。毕竟，我们需要以某种方式表示它们——而当试图在计算机中存储和处理它们时，允许它们变得过大是有问题的。

所以是的，整数——更具体地说，正整数——但我们还差一步。我们需要一种方法来保持我们的值在控制范围内（有界的），同时还要弄清楚如何处理除法。

模运算

为了弥补这一点，我们将使用一个简单的工具：模运算 和模运算。

我在以前的文章中谈过这些内容，所以我假设你对此概念是熟悉的。

通过使用模运算来约束加法、减法和乘法运算的结果，我们基本上将可以操作的可能整数限制在一个有限的集合中，比如这个：

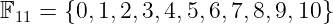
我们在这里使用符号 𝔽，因为生成的集合将是一个域（因此是 𝔽）。域只是一个加法、减法、乘法和除法都被定义良好的集合。

这样一个问题解决了（有界性）。现在我们的域是一个有限的集合，我们称之为有限域。

除法需要更多的工作——还有一个聪明的观察。

另一种视角

以5 mod 3为例。显然，结果是2。我们是如何得到这个结果的？

我们可以更严格地描述这个过程为找到这个方程的解：

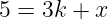
并且要求 x 的值在 0 和 4 之间（𝔽₅ 的一个元素）。这将得到 k = 1 和 x = 2。

然而，很明显，其他的解是存在的。例如，k = 2 和 x = -1。正如你现在可能猜到的，我们可以找到无穷多个整数解。

实际上，所有可能的 x 的值的集合形成了一个等价类。

好的……我们为什么要关心这件事呢？结果发现，通过这样的方式来看，有什么我们可以做的关于除法的事情！

如果我们仔细想一下，某些除法 1 / a 的结果无非是一个其他的数字，满足某个特定的属性。例如，1 / 2 的结果是 0.5，而 1 / 3 的结果是 0.333(…)。这些结果都分享这个属性：

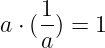
因此，与其把它看作是除法，我们不如把它看作是找到倒数数字。我们问自己：

给定我们域中的某个数字，我们能否找到另一个数字（也在该域中），使得当我们将它们相乘时，结果是1？

换句话说，我们在找这个方程的解：

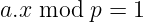
而——你大概猜到了——可以转换成这个形式：

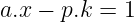
我们又回到了之前的场景！如果我们有权找到一个有效的 x 值，我们称它为 a 的模逆，并将其写作 a⁻¹。

太棒了

这一形式被称为**[贝祖恒等式](https://en.wikipedia.org/wiki/B%C3%A9zout%27s_...