ZK中的32位仿真
- RareSkills
- 发布于 7小时前
- 阅读 32
本文介绍了如何在零知识证明（ZK）电路中模拟32位算术运算，由于ZK默认数据类型是有限域元素，而实际计算常用32位、64位或256位数字，因此需要用域元素来模拟传统数据类型。文章详细讲解了32位范围检查、加法、乘法、除法与取模、位移以及位运算的实现方法，并提供了相应的Circom代码示例，同时还讨论了ZK EVM如何处理256位数字。
ZK 中默认的数据类型是域元素，所有的算术运算都是在一个大素数的模下进行的。然而，大多数 “实际” 计算都是使用 32 位、64 位或 256 位的数字完成的，具体取决于虚拟机或执行环境。
为什么我们需要 32 位仿真？
许多密码学哈希函数都在 32 位字上运行，因为从历史上看，32 位是许多 CPU 的默认字长。后来增加到 64 位。EVM 使用 256 位，以便能够轻松地容纳 keccak256 哈希。
如果我们想使用 ZK 来证明传统哈希函数或某些不使用有限域的虚拟机（大多数都不使用）的正确执行，那么我们需要用一个域元素来 “建模” 传统的数据类型。因此，我们在 Circom 中使用一个域元素（信号）来保存一个不能超过 32 位数字可以保存的数字，即使该信号可以保存比 32 位大得多的值。
32 位字 vs 有限域元素
32 位字和有限域元素之间的关键区别在于它们溢出的点。在 Circom 中，或任何使用 bn128 曲线的语言中，溢出发生在 p 处，其中 p = 21888242871839275222246405745257275088548364400416034343698204186575808495617。在 32 位机器中，溢出发生在 4294967296，或者更一般地说，发生在 2n 处，其中 n 是虚拟机中的位数。
可以将 32 位虚拟机看作是以 232 为模进行所有算术运算。默认情况下，普通虚拟机在该数字处溢出。然而，当在有限域中进行模运算时，计算模 232 会增加相当多的约束（我们稍后会看到），但幸运的是，有一个有用的数学技巧可以有效地做到这一点。
以下两个函数在计算模 232 时是等效的：
contract DemoMod32 {
function mod32(uint256 x) public pure returns (uint256) {
return x % (2**32);
}
function mod32e(uint256 x) public pure returns (uint256) {
// only keep the 32 least significant bits
return uint256(uint32(x));
}
}我们可以通过仅保留 32 个最低有效位来计算 mod232。对此的形式化验证在附录中。在我们对包含 32 位数字的信号进行任何算术运算之前，我们首先需要完全确定该信号保存的数字实际上适合 32 位。
32 位范围检查
如果我们正在创建一个 ZK 电路，该电路使用 32 位字来模拟计算，那么我们需要确保没有信号保存大于或等于 232 的值。一个直观的做法是使用 LessThan 模板，如下所示：
signal safe;
safe <== LessThan(252)([x, 2**32]);
safe === 1;但是，此电路创建的约束比必要的更多。
一种更有效的方法是利用二进制表示。关键思想是用 32 位编码一个数字，如果它适合 32 位，则电路正常执行。相反，如果该数字不适合 32 位，则无法满足约束。因此，下面的电路确保 in 是 232−1 或更小。
include "circomlib/comparators.circom";
// 8 bit range check
template RangeCheck() {
signal input in;
component n2b = Num2Bits(32);
n2b.in <== in;
}
component main = RangeCheck();
// if in = 2**32 - 1, it will accept
// if in = 2**32 it will reject没有必要像使用 LessThan 那样约束 Num2Bits 的输出，因为在内部，它已经将 out 约束为零或一，并且还约束二进制表示等于输入（通过 lc1 === in），这可以在下面的 Num2Bits 模板中看到：
template Num2Bits(n) {
signal input in;
signal output out[n];
var lc1=0;
var e2=1;
for (var i = 0; i<n; i++) {
out[i] <-- (in >> i) & 1;
out[i] * (out[i] -1 ) === 0; // CONSTRAINT HAPPENS HERE
lc1 += out[i] * e2;
e2 = e2+e2;
}
lc1 === in;
}
32 位加法
假设我们想将两个域元素 x 和 y 相加，它们代表 32 位数字。
32 位加法的简单实现是将域元素转换为 32 位，然后构建一个 “加法电路”，该电路将每个位相加并进位溢出。但是，这样会创建比必要的更大的电路。
相反，我们可以这样做：
- 使用上述策略范围检查
x和y - 将
x和y作为域元素相加，即z <== x + y - 将
z转换为 33 位数字 - 将 33 位数字的最低有效 32 位转换为域元素。
这可以可视化如下：
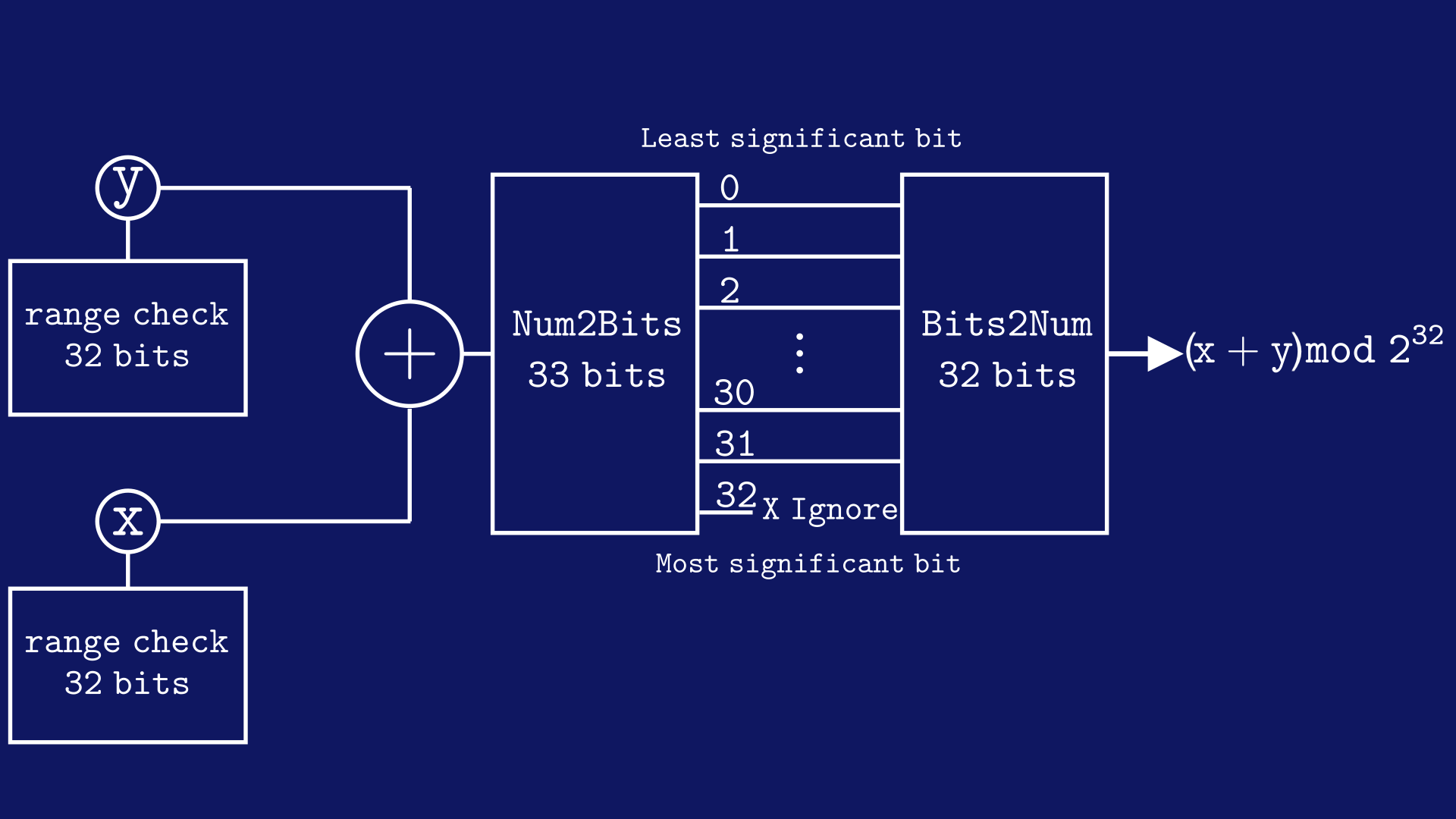
x + y 最多可以溢出到 33 位数字。考虑 x 和 y 可以保持的最大值是 232−1。如果我们将该值添加到自身，我们得到
(232−1)+(232−1)=2⋅(232−1)=233−2
最终数字需要 33 位才能保持。（回想一下，33 位可以保持的最大数字是 233–1。因此，上面的数字是 33 位可以保持的第二大数字。）因此，我们只需要 33 位来保持总和，然后我们删除第 33 位。
下面是使用 Circom 模拟和验证 32 位加法的代码：
include "circomlib/comparators.circom";
include "circomlib/bitify.circom";
template Add32(n) {
signal input x;
signal input y;
signal output out;
// range check x and y
component rCheckX = Num2Bits(32);
component rCheckY = Num2Bits(32);
rCheckX.in <== x;
rCheckY.in <== y;
// convert the sum to 33 bits
component n2b33 = Num2Bits(33);
n2b33.in <== x + y;
// convert the least significant 32 bits
// to the final result
component b2n = Bits2Num(32);
for (var i = 0; i < 32; i++) {
b2n.in[i] <== n2b33.out[i];
}
b2n.out ==> out;
}32 位乘法
32 位乘法的逻辑与 32 位加法非常相似，只是我们需要允许 32 位乘法在仅保存最终 32 位之前临时需要最多 64 位：
=(232−1)(232−1)=264−232−232+2=264−233+2
最终数字需要 64 位才能保持。
此电路的实现留给读者作为练习。
32 位除法和取模
整数除法是 ZK 中最具问题的错误之一，因为正确约束它比加法和乘法的示例困难得多。以下是一些在实际应用中约束不足的除法的例子：
- <https://code4rena.com/reports/2023-10-zksync#h-01-missing-range-constraint-on-remainder-check-in-div-opcode-implementation>
- <https://github.com/succinctlabs/sp1/issues/746>
在整数除法中，分子、分母、商和余数之间的关系是：
numerator=denominator×quotient+remainder
但是，仅凭该约束不足以确保除法已正确执行。
例如，假设我们试图证明我们计算了 12 / 7 = 1。我们的电路将具有以下值
12=7×1+5
但是，以下 witness 也满足约束：
12=7×0+12
我们可以通过添加约束来防止这种情况，即余数严格小于分母。
此外，我们应该注意以下潜在错误：
- 这不是 254 位字段中 32 位的担忧（这是 Circom 使用的默认值），但我们希望确保计算 denominator×quotient 不会溢出底层有限域。
- 更一般地说，我们不希望计算 denominator×quotient+remainder 溢出。如果
denominator和quotient的范围检查为 32 位，那么乘积 denominator×quotient 可以保持的最大位数为 64 位，如果remainder的范围检查为 32 位，则 denominator×quotient+remainder 可以需要的最大位数为 65 位。因此，使用 32 位的 VM 位大小不是 Circom 默认字段的担忧，但对于其他 VM 位大小，例如 128 位，可能会发生溢出。 - 除以零可能会产生意想不到的行为，具体取决于你正在考虑的 ZKVM。例如，EVM 在发生除以零时不会 panic，而是返回零。在 RISC-V 架构中，除以零会返回一个所有位都设置为 1 的字。
仅使用加法和乘法直接计算整数除法是不切实际的（乘法的 Karatsuba 方法 或 高效整数除法 等高效算法使用 for 循环或递归，这不能很好地映射到加法和乘法），因此最好在约束之外计算整数除法结果。
在 Circom 中，/ 运算符是指模除法（乘以乘法逆元），而 \ 运算符是指整数除法。以下代码显示了如何证明我们正确计算了商和余数。我们包括余数的计算，因为当我们证明我们正确计算了整数除法时，我们可以免费获得它。
include "circomlib/comparators.circom";
include "circomlib/bitify.circom";
template DivMod(wordSize) {
// a wordSize over this could overflow 252
assert(wordSize < 125);
signal input numerator;
signal input denominator;
signal output quotient;
signal output remainder;
quotient <-- numerator \ denominator;
remainder <-- numerator % denominator;
// quotient and remainder still need
// to be range checked because the
// prover can supply any value
// range check all the signals
component n2bN = Num2Bits(wordSize);
component n2bD = Num2Bits(wordSize);
component n2bQ = Num2Bits(wordSize);
component n2bR = Num2Bits(wordSize);
n2bN.in <== numerator;
n2bD.in <== denominator;
n2bQ.in <== quotient;
n2bR.in <== remainder;
// core constraint
numerator === quotient * denominator + remainder;
// remainder must be less than the denominator
signal remLtDen;
// depending on the application, we might be able
// to use fewer than 252 bits
remLtDen <== LessThan(wordSize)([remainder, denominator]);
remLtDen === 1;
// denominator is not zero
signal isZero;
isZero <== IsZero()(denominator);
isZero === 0;
}
component main = DivMod(32);32 位位移
假设我们希望模拟以下代码：
uint32 x;
uint32 s;
x << s;左移 s 相当于乘以 2s，其中 s 是位移的大小，而右移 s 相当于除以 2s。如上一章所示，计算幂可以创建相当大的约束集。因此，通常更有效的方法是预先计算每个 2 的幂，直到字大小减 1。因此，对于 32 位数字的左移，我们预先计算每个 2 的幂，直到 31（字大小 (32) – 1）：1、2、4、8、…、231，并使用前面讨论的条件选择技术将 x 乘以适当的选择。如果位移量为 32 或更大，我们将乘以零。
此实现留给读者作为练习。
32 位 AND、NOT、OR、XOR 和 NOT
Circomlib gates 库 具有每个这些电路的实现，并且它们是不言自明的，因此我们鼓励读者简单地阅读那里的代码。我们在下面展示了如何模拟以下操作的模板：
按位与
uint32 a;
uint32 b;
a & b;按位非
uint32 x;
~x; // 翻转所有位以下是计算和约束 a 和 b 的按位与的代码。
include "circomlib/gates.circom";
include "circomlib/bitify.circom";
template BitwiseAnd32() {
signal input a;
signal input b;
signal output out;
// range check
component n2ba = Num2Bits(32);
component n2bb = Num2Bits(32);
n2ba.in <== a;
n2bb.in <== b;
component b2n = Bits2Num(32);
component Ands[32];
for (var i = 0; i < 32; i++) {
Ands[i] = AND();
Ands[i].a <== n2ba.out[i];
Ands[i].b <== n2bb.out[i];
Ands[i].out ==> b2n.in[i];
}
b2n.out ==> out;
}
component main = BitwiseAnd32();剩余的 NOT、OR 和 XOR 操作留给读者作为练习。
ZK EVM 如何处理 256 位数字
默认的 Circom 字段无法容纳 256 位数字。相反，EVM 中的每个 word 都必须使用较小字大小的列表来建模，类似于 64 位计算机如何模拟 EVM。
例如，一个 256 位数字可以用四个 64 位字来建模。添加时，我们将从不太重要的字中进位溢出到下一个重要字。如果最重要的字溢出，我们只需丢弃溢出。
附录 A：等效性证明
我们使用 Certora 证明器来演示以下函数的等效性：
contract DemoMod32 {
function mod32(uint256 x) public pure returns (uint256) {
return x % (2**32);
}
function mod32e(uint256 x) public pure returns (uint256) {
// only keep the 32 least significant bits
return uint256(uint32(x));
}
}这是 Certora 验证语言规则：
methods {
function mod32(uint256) external returns (uint256) envfree;
function mod32e(uint256) external returns (uint256) envfree;
}
rule test_Mod32AndMod32E_Equivalence() {
uint256 x;
assert mod32(x) == mod32e(x);
}这是 Certora 报告：
- 原文链接： rareskills.io/post/emula...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
