姚期智 - 姚氏百万富翁
- asecuritysite
- 发布于 2025-04-27 09:19
- 阅读 1940
本文介绍了图灵奖得主姚期智的贡献,包括姚氏百万富翁问题和混淆电路。姚氏百万富翁问题是一种在不泄露各自财富的情况下,比较两个百万富翁财富多少的方法。混淆电路则是一种在不信任对方的情况下,进行安全计算的方法,文章提供了RSA加密算法和混淆电路的Python代码示例。

姚期智
当我读到更多关于姚期智的信息时,我不得不笑了……
“他要求他们使用 LaTeX 编写练习,这是一种专门为撰写论文而设计的软件包。”
我之所以笑,是因为我自己的学生目前也在用 LaTeX 撰写他们的密码学课程作业。教育应该是关于卓越和推动自己学习新事物,而且没有什么比 LaTeX 更适合分享研究成果了。
姚期智出生于 1946 年,目前是清华大学的院长[ 这里]。他实际上获得了两个博士学位。第一个是 1972 年在哈佛大学获得的物理学博士学位,第二个是 1975 年在伊利诺伊大学获得的计算机科学博士学位。之后,他在斯坦福大学和加州大学伯克利分校工作。他最早的主要贡献之一是姚氏测试 [3],其中一系列单词通过他的测试,如果它们无法与随机生成区分开来。
总的来说,他是一位世界级的研究人员,并且是一位归化的美国公民,但在 2014 年,他决定搬回中国,以加强其出生国家的研究。2000 年,他被授予 ACM 图灵奖(相当于计算机科学领域的诺贝尔奖)[ 这里]:
2021 年,姚期智获得了京都奖:
姚氏百万富翁问题
在姚氏 1982 年的论文[2]中,他概述了一个问题,即找到一种方法,让两位百万富翁找出他们中谁的钱最多,而且他们不信任任何人来确定这一点,并且他们不会透露他们有多少钱:

这是多方计算(MPC)和零知识证明的开始。在百万富翁问题中,我们可以确定两位百万富翁中谁的钱最多,而无需他们透露自己的钱。该方法涉及我们使用 RSA 加密。为此,我使用了此处的示例 4:
e=79
d=1019
N=3337并选择一个素数:
p=631我们将 I 定义为 Bob 的百万,J 定义为 Alice 的百万:
J =4
I =5接下来,我们选择一个随机数 U:
U=randint(0,2000)并计算 C 值(这是 RSA 加密过程):
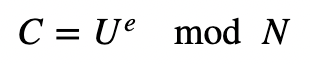
现在 Alice 计算:
C - J + 1她与 Bob 分享这个,然后 Bob 计算 10 个值:
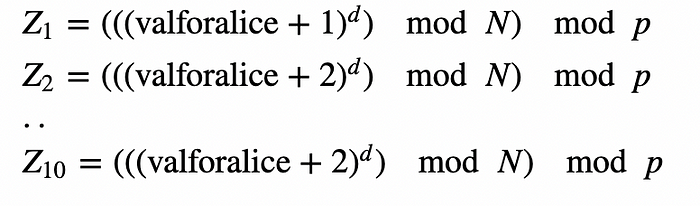
然后 Bob 获取这些值,如果对于第 i 个值,以及其余的值,他会将 1 加到该值上。然后将这些值发送回 Alice。
Alice 现在计算:
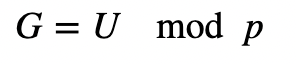
如果第 j 个值与 G 相同,则 Alice 的钱更多或相同,否则 Bob 的钱更多。
乱码电路
1986 年,姚期智发明了乱码(或加扰)电路的概念,这是一种以私密方式传递信息并仍然对其进行处理的方式 [ 1]:

假设 Bob 和 Alice 互不信任。他们的关系很糟糕,但他们仍然想做出一些决定,甚至不再信任他们的律师。然后他们同意一项安全协议,他们必须都同意某件事(A & B),或者他们中的一个必须同意(A 或 B),或者当只有一方同意而另一方不同意时(A xor B)。这是一个简单的逻辑函数。
假设他们同意都同意某件事,所以我们有一个 AND 函数(A & B)。我们现在创建一个加扰的 AND 门。为此,我们得到:
A B Z
0 0 0
0 1 0
1 0 0
1 1 1现在 Bob 创建了四个加密密钥 K(a=0)、K(a=1)、K(b=0) 和 K(b=1)。现在他将继续并使用与这些位相关的两个加密密钥来加密四个可能的输出(在本例中为“0”、“0”、“0”和“1”)。例如,输出:
A=0, B=0, Z=0将使用 K(a=0) 和 K(b=0) 的密钥加密输出(“0”)。
在 Python 中,这是代码 [ 这里]:
keyX_0 = Fernet.generate_key()
keyX_1 = Fernet.generate_key()
keyY_0 = Fernet.generate_key()
keyY_1 = Fernet.generate_key()
data =[]
for a in range(0,2):
for b in range(0,2):
data.append(str(eval(operator) & 0x01))
cipher_text00 = Fernet(keyY_0).encrypt(Fernet(keyX_0).encrypt(data[0]))
cipher_text01 = Fernet(keyY_0).encrypt(Fernet(keyX_1).encrypt(data[1]))
cipher_text10 = Fernet(keyY_1).encrypt(Fernet(keyX_0).encrypt(data[2]))
cipher_text11 = Fernet(keyY_1).encrypt(Fernet(keyX_1).encrypt(data[3]))然后 Bob 将 cipher_text 值(cipher_text00 … cipher_text11)传递给 Alice,并提供他输入的密钥。如果他说 YES,那么他传递 keyX_1,否则,他将传递 keyX_0。
现在 Alice 收到四个值和 Bob 的密钥。现在她使用不经意传输来获得她答案的密钥。如果她说 YES,我们获得 keyY_1 的密钥,而 Bob 实际上并不知道他说了 YES。如果她说 NO,她得到 keyY_0。
最后,她将有两个密钥,并且她尝试所有密码:
try:
print Fernet(keyB).decrypt(Fernet(keyA).decrypt(cipher_text00))
except:
print ".",
try:
print Fernet(keyB).decrypt(Fernet(keyA).decrypt(cipher_text01))
except:
print ".",
try:
print Fernet(keyB).decrypt(Fernet(keyA).decrypt(cipher_text10))
except:
print ".",
try:
print Fernet(keyB).decrypt(Fernet(keyA).decrypt(cipher_text11))
except:
print ".",她唯一能打开的是与 Bob 和 Alice 的决定相匹配的那个。
为了说明这一点,假设 Bob 和 Alice 都说“No”,所以他们对 AND 函数的输入将是 0 和 0。现在 Bob 用四个密钥加密四个输出,但是唯一能打开输出的是 A 输入为 0 和 B 输入为 0 的密钥。Bob 传递他的密钥,而不透露他的输入为 K(a=0),而 Alice 通过不经意传输收到她的密钥:
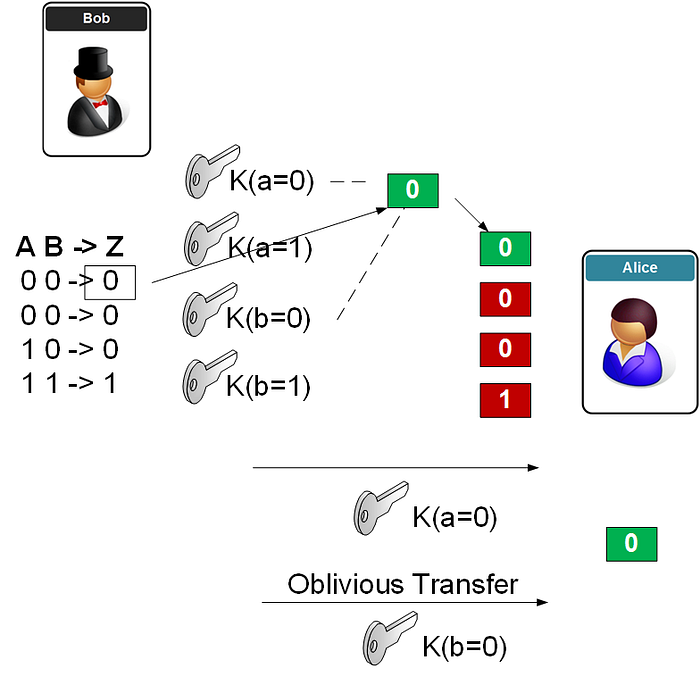
演示在此。
结论
我喜欢有人对他们的工作充满热情:
“如果我们走正确的道路,清华大学在计算机科学方面的努力将在未来几年内带来重大的科学突破。如果我们继续努力,清华大学的计算机科学课程将在未来成为世界一流的学科”
参考文献
[1] Yao, A. C. C. (1986, October). How to generate and exchange secrets. In 27th Annual Symposium on Foundations of Computer Science (sfcs 1986) (pp. 162–167). IEEE.
[2] Yao, A. C. (1982, November). Protocols for secure computations. In 23rd annual symposium on foundations of computer science (sfcs 1982) (pp. 160–164). IEEE.
[3] Yao, A. C. (1982, November). Theory and application of trapdoor functions. In 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982) (pp. 80–91). IEEE.
[4] Yao AC-C (1977) Probabilistic computations: Toward a unified measure of complexity. In Proceedings of IEEE 18th Annual Symposium on Foundations of Computer Science (sfcs 1977), IEEE: 222–227.
[5] Yao AC-C (1979) Some Complexity Questions Related to Distributive Computing (Preliminary Report) In Proceedings of the 11th Annual ACM Symposium on Theory of Computing (STOC ’79), ACM: 209–213.
[6] Dolev D & Yao AC-C (1983) On the security of public key protocols. IEEE Transactions on Information Theory 29 (2): 198–208.
[7] Yao AC-C (1993) Quantum Circuit Complexity. In Proceedings of IEEE 34th Annual Symposium on Foundations of Computer Science (FOCS 1993), IEEE: 352–361.
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 224 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 172 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 229 浏览
- Zcash:比特币遗忘的隐私 362 浏览
- ZK编年史:计算模型 258 浏览
- lambdaworks 2026 年更新路线图和优先级 310 浏览
- 2026年构建机构级DeFi平台真正需要什么 680 浏览
- zkMesh:2026年1月回顾 377 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 497 浏览
- Zcash 的时代到来了 577 浏览
- ZK 编年史:电路(第二部分) 374 浏览
- Vitalik: 2026年我对使用的软件做了两个重大改变 504 浏览

