以太坊中更快的区块/blob传播 - 网络
- 以太坊中文
- 发布于 2025-04-23 15:11
- 阅读 1200
本文提出了一种使用随机线性网络编码(RLNC)来改进以太坊中区块和blob传播的方法。该方法将区块分割成多个chunk,并使用线性组合进行广播,从而减少了传输时间和带宽消耗。实验证明,该方法可以显著降低延迟和带宽浪费,尤其是在处理大区块或blob时,能有效提升网络性能。
以太坊中更快的区块/blob传播
感谢 @n1shantd, @ppopth 和 Ben Berger 对本文的讨论和反馈,以及 @dankrad(https://ethresear.ch/u/dankrad)的许多有益讨论。
摘要
我们建议通过使用随机线性网络编码来改变我们在 P2P 网络中广播和传输区块和 blob 的方式。我们证明,从理论上讲,我们可以以当前 gossipsub 实现所需时间的 5% 的带宽和 57% 的网络跳数(因此每个消息的延迟减半)来分发区块。我们提供了计算开销的具体基准。
介绍
目前用于分发区块的 gossipsub 机制大致如下。提议者在其所有对等方中选择一个随机子集(称为其 Mesh),其中 D=8 个对等方,并将其区块广播给他们。每个接收到区块的对等方都执行一些非常快的初步验证:主要是签名验证,但最重要的是不包括状态转换或事务执行。经过此快速验证后,对等方将其区块重新广播到另外 D 个对等方。这种设计有两个直接的后果:
- 每次跳跃至少增加以下延迟:从一个对等方到下一个对等方的一个完整区块传输(包括网络 ping 延迟,基本上与带宽无关,加上完整区块的传输,受带宽限制)。
- 对等方不必要地将完整区块广播到已经接收到完整区块的其他对等方。
我们建议在广播级别使用 随机线性网络编码 (RLNC)。通过这种编码,提议者会将区块拆分为 N 个块(例如,对于下面的所有模拟,N=10),并且不是将完整区块发送给大约 8 个对等方,而是将单个块发送给大约 40 个对等方(不是原始块之一,而是它们的随机线性组合,有关隐私注意事项,请参见下文)。对等方仍然需要下载一个完整的区块,或者更确切地说,N 个块,但是他们可以从不同的对等方并行获取它们。在他们收到这 N 个分别是由组成原始区块的原始块的随机线性组合的块之后,对等方需要求解一个线性方程组以恢复完整区块。
一个概念验证 实现 突出了以下数字
- 提出一个区块需要额外的 26 毫秒,这是受 CPU 限制的,并且可以在现代笔记本电脑(Apple M4 Pro)上完全并行化为小于 2 毫秒
- 验证每个块需要 2.6 毫秒。
- 解码完整区块需要 1.4 毫秒。
- 使用
10个块和D=40,每个节点发送的数据量是当前 gossipsub 的一半,并且网络以一半的时间广播一个 100KB 的区块,并且随着区块大小的增加而受益。
协议
有关网络编码的深入介绍,我们建议读者阅读 原引 和 这本教科书。我们在此处提及上述引用的概念验证基准的最低实现详细信息。在区块传播(约 110KB)的情况下,延迟或网络跳数支配着传播时间,而在完整 DAS 中像 blob 这样的大消息的情况下,带宽支配着传播时间。
我们考虑一个具有素数特征的有限域 \mathbb{F}_p。在上面的示例中,我们选择了由 curve25519-dalek rust crate 实现的 Ristretto 标量基域。提议者获取一个区块,该区块是不透明的字节切片,并将其解释为 \mathbb{F}_p 中的元素向量。在撰写本文时,一个典型的以太坊区块约为 B = 110KB,鉴于每个 Ristretto 标量需要不到 32 个字节来编码,因此一个区块大约需要 B/32 = 3520 个 \mathbb{F}_p 的元素。分成 N=10 个块,每个块都可以看作是 \mathbb{F}_p^{M} 中的向量,其中 M \sim 352。因此,该区块被视为 N 个向量 v_i \in \mathbb{F}^M_p, i=1,...,N。提议者随机选择 D\sim 40 个对等方的子集。对于每个这样的对等方,它将发送一个 \mathbb{F}_p^M 的向量,以及一些额外的信息来验证消息并防止网络上的 DOS。我们解释一下提议者
提议者
我们将使用 Pedersen 承诺到 Ristretto 椭圆曲线 E,如上面提到的 rust crate 所实现的那样。我们假设我们已经随机选择了足够元素 G_j \in E, j = 1, ..., K 的可信设置,其中 K \gg M。我们选择 \mathbb{F}_p^M 的标准基 \{e_j\}_{j=1}^M。因此,每个向量 v_i 都可以唯一地写成
v_i = \sum_{j=1}^M a_{ij} e_j,
对于某个标量 a_{ij} \in \mathbb{F}_p。对于每个向量 v_i,我们都有一个 Pedersen 承诺
C_i = \sum_{j=1}^M a_{ij}G_j \in E.
最后,对于大小为 D \sim 40 的子集中的每个对等方,提议者均匀地随机选择标量 b_i, i=1, ...,N 的集合,并将以下信息发送给该对等方
- 向量 v = \sum_{i=1}^N b_i v_i \in \mathbb{F}_p^M。它的大小为 32M 字节,也是消息的内容。
- N 个承诺 C_i, i=1,...,N。这是 32N 字节。
- N 个系数 b_i, i=1, ...,N。这是 32N 字节。
- N 个承诺 C_1 || C_2 || ... || C_N 的哈希的 BLS 签名,这是 96 字节。
一个 签名消息 是上述元素 1-4 的集合。我们看到,作为附带信息,每条消息会额外发送 64N \sim 640 字节。
接收对等方
当对等方收到上一节中的消息时,验证过程如下
- 它验证签名对于提议者和接收承诺的哈希是否有效。
- 它写入接收向量 v = \sum_{j=1}^M a_j e_j,然后计算 Pedersen 承诺 C = \sum_{j=1}^M a_j G_j。
- 接收到的系数 b_i 声明 v = \sum_{i=1}^N b_i v_i。对等方计算 C'= \sum_{i=1}^N b_i C_i,然后验证 C = C'。
对等方跟踪他们收到的消息,假设它们是向量 w_i, i = 1,...,L,其中 L < N。他们生成一个子空间 W \subset \mathbb{F}_p^M。当他们收到 v 时,他们首先检查该向量是否在 W 中。如果是,则他们会丢弃它,因为该向量已经是先前向量的线性组合。该协议的关键是这种情况发生的可能性非常小(对于上面的数字,这种情况发生的概率远小于 2^{-256})。作为推论,当节点收到 N 条消息时,它知道它可以从消息 w_i, i=1,...,N 中恢复原始 v_i,从而恢复区块。
还要注意,只需要一个签名验证,所有传入消息都具有相同的承诺 C_i 和对同一组承诺的相同签名,因此对等方可以缓存第一个有效验证的结果。
发送对等方
对等方可以在收到一个块后立即将块发送给其他对等方。假设一个节点拥有 w_i, i=1,...,L,其中 L \leq N,如上一节中所述。一个节点还会跟踪他们收到的标量系数,因此他们知道他们拥有的块满足
w_i = \sum_{j=1}^N b_{ij} v_j \quad \forall i,
对于保存在其内部状态中的某些标量 b_{ij} \in \mathbb{F}_p。最后,节点还保留来自提议者的完整承诺 C_i 和签名,他们在验证他们收到的第一个块时已对其进行验证。
节点发送消息的过程如下。
- 他们随机选择 L 个标量 \alpha_i \in \mathbb{F}_p, i=1,...,L。
- 他们形成块 w = \sum_{i=1}^L \alpha_i w_i。
- 他们通过以下方式形成 N 个标量 a_j, i=1,...,N
a_j = \sum_{i=1}^L \alpha_i b_{ij}, \quad \forall j=1,...,N.
他们发送的消息包含块 w、系数 a_j 和承诺 C_i 以及来自提议者的签名。
基准
该协议与 gossipsub 有一些共同的组件,例如,提议者需要进行一个 BLS 签名,而验证者必须检查一个 BLS 签名。我们在此记录了除通常的 gossipsub 操作之外还需要执行的操作的基准。这些是协议在节点上具有的 CPU 开销。基准测试已在 Macbook M4 Pro 笔记本电脑和 Intel i7-8550U CPU @ 1.80GHz 上进行。
这些基准测试的参数是 N=10 表示块的数量,并且总块大小被认为是 118.75KB。所有基准测试都是单线程的,并且都可以并行化
提议者
提议者需要执行 N 个 Pedersen 承诺。经基准测试为
| 计时 | 模型 |
|---|---|
| [25.588 ms 25.646 ms 25.715 ms] | Apple |
| [46.7ms 47.640 ms 48.667 ms] | Intel |
节点
接收节点需要为每个块计算 1 个 Pedersen 承诺,并执行相应的由提议者提供的承诺的线性组合。这些的计时如下
| 计时 | 模型 |
|---|---|
| [2.6817 ms 2.6983 ms 2.7193 ms] | Apple |
| [4.9479 ms 5.1023 ms 5.2832 ms] | Intel |
发送新块时,节点需要执行其可用块的线性组合。这些的计时如下
| 计时 | 模型 |
|---|---|
| [246.67 µs 247.85 µs 249.46 µs] | Apple |
| [616.97 µs 627.94 µs 640.59 µs] | Intel |
在收到 N 个块后解码完整区块时,节点需要求解一个线性方程组。计时如下
| 计时 | 模型 |
|---|---|
| [2.5280 ms 2.5328 ms 2.5382 ms] | Apple |
| [5.1208 ms 5.1421 ms 5.1705 ms] | Intel |
总体 CPU 开销。
Apple M4 上提议者的总体开销是 26 毫秒(单线程),而对于接收节点,它是 29.6 毫秒(单线程)。这两个过程都可以完全并行化。在提议者的情况下,它可以并行计算每个承诺,而在接收节点的情况下,这些是自然并行事件,因为节点正在从不同的对等方并行接收块。在 Apple M4 上并行运行这些过程会导致提议者方面为 2.6 毫秒,接收对等方为 2.7 毫秒。对于实际应用,与所涉及的网络延迟相比,将这些开销视为零是合理的。
优化
一些尚未实现的过早优化包括在块到达时反转线性系统,尽管上面引用的概念验证确实将传入的系数矩阵保持在 Echelon 形式。最重要的是,消息的随机系数不需要像 Ristretto 字段那样大的字段。像 \mathbb{F}_{257} 这样的小素数字段就足够了。但是,由于 Pedersen 承诺发生在 Ristretto 曲线中,因此我们被迫在更大的字段中执行标量运算。这些基准测试的实现为线性组合选择了小系数,并且这些系数在每次跳跃时都会增长。通过正确地控制和选择随机系数,我们可能能够将线性系统的系数(以及因此在发送块时的带宽开销)限制为使用例如 4 个字节而不是 32 个字节进行编码。
执行这种优化最简单的方法是在 \mathbb{F}_q 上定义的椭圆曲线上工作,其中 q = p^r 对于某个小素数 p。这样,可以在子域 \mathbb{F}_p \subset \mathbb{F}_q 上选择系数。
隐私注意事项 上面链接的 PoC 中的实现认为每个节点,包括提议者,都选择小系数来复合其线性变换。这允许接收具有小系数的块的对等方识别该块的提议者。要么采用上述优化来通过执行像 Bareiss 展开这样的算法来保持所有系数都很小,要么我们应该允许提议者从字段 \mathbb{F}_p 中选择随机系数。
模拟
我们在一些简化假设下进行了块传播的模拟,如下所示。
- 我们选择一个随机网络,该网络建模为一个有向图,具有 10000 个节点,并且每个节点都有 D 个对等方可以向其发送消息。D 在本说明中称为 Mesh 大小,并且选择在 3 到 80 的较大范围内变化。
- 对等方是在整个节点集中随机且均匀地选择的。
- 每个连接都选择具有相同的 X MBps 带宽(通常在以太坊中假定为 X=20,但我们可以将此数字保留为一个参数)
- 每次网络跳跃都会产生 L 毫秒的额外恒定延迟(通常测量为 L=70,但我们可以将此数字保留为一个参数)
- 消息大小假定为 B KB 的总大小。
- 对于 RLNC 模拟,我们使用 N=10 个块来分割该块。
- 每次节点将消息发送给对等方,但由于消息是冗余的(例如,对等方已经拥有完整块)而被丢弃时,我们都会将消息的大小记录为 浪费的带宽。
Gossipsub
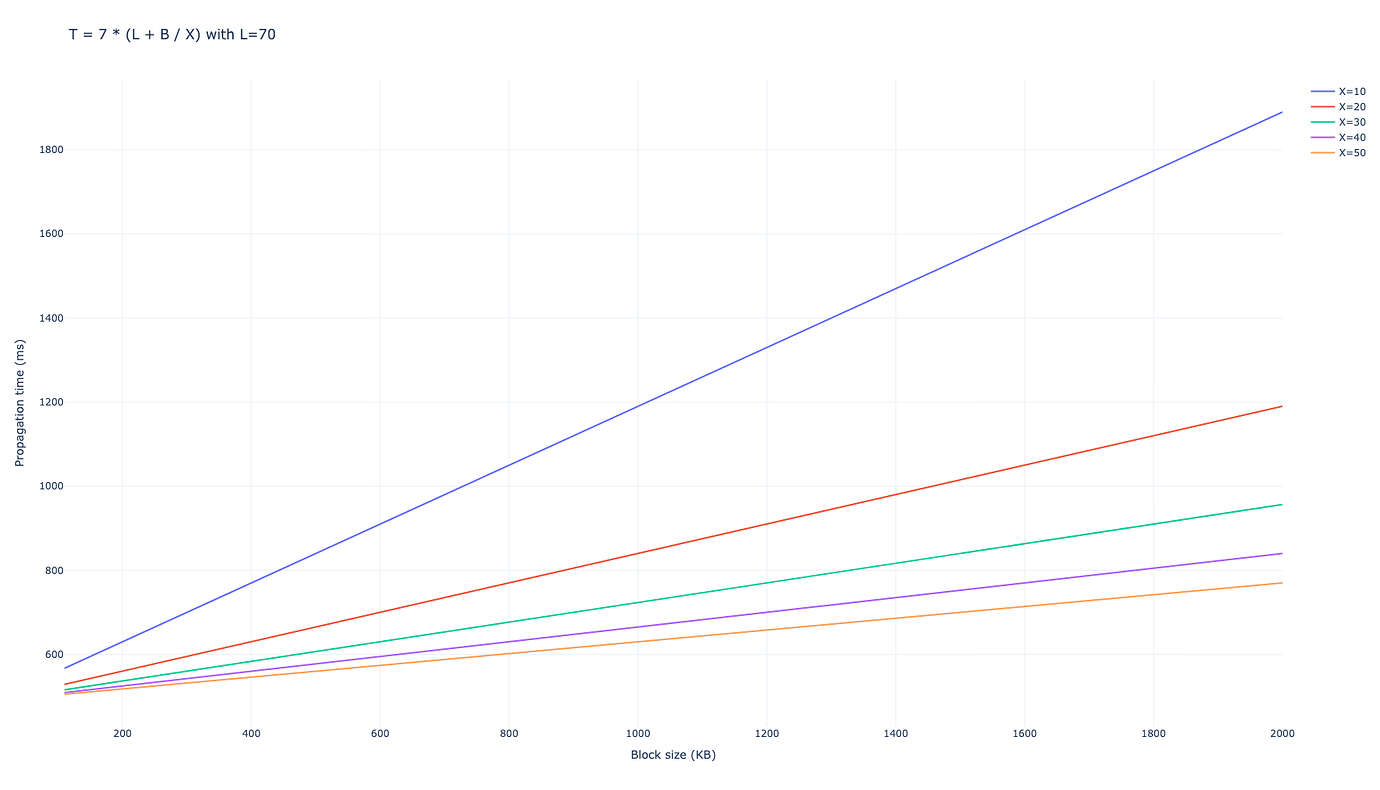
我们使用对等方数量来发送消息 D=6。我们获得网络平均需要 7 跳才能将完整块传播到 99% 的网络,从而导致总传播时间为
T_{\mathrm{gossipsub, D=6}} = 7 \cdot (L + B/X),
以毫秒为单位。
 \
gossipsub-total-theorical1712×982 70.6 KB
\
gossipsub-total-theorical1712×982 70.6 KB
当 D=8 时,结果相似
T_{\mathrm{gossipsub, D=8}} = 6 \cdot (L + B/X),
浪费的带宽对于 D=6 为 94,060 \cdot B,对于 D=8 为 100,297 \cdot B。
对于 B 的低值(例如当前的以太坊区块),延迟支配着传播,而对于更大的值(例如在 peer-DAS 之后传播 blob),带宽成为主要因素。
RLNC
每个对等方一个块
使用随机线性网络编码,我们可以使用不同的策略。我们模拟了一个系统,其中每个节点只会将一个块发送到其大小为 D 的 Mesh 中的所有对等方,这样我们保证了产生的延迟与 gossipsub 中的延迟相同:每次跳跃的单个延迟成本为 L 毫秒。这要求网格大小明显大于 N,即块的数量。请注意,对于 gossipsub 网格大小 D_{gossipsub}(例如当前以太坊中的 8),我们将需要设置 D_{RLNC} = D_{gossipsub} \cdot N 以消耗每个节点相同的带宽,对于当前值,这将是 80。
对于保守得多的带宽值,即 D=40,我们获得
T_{RLNC, D=40} = 4 \cdot \left(L + \frac{B}{10 X} \right),
浪费的带宽为 29,917\cdot B。假设与今天相同的带宽,我们得到 D=80,我们得到令人印象深刻的
T_{RLNC, D=80} = 3 \cdot \left(L + \frac{B}{10 X} \right),
浪费的带宽为 28,124\cdot B,这是 gossipsub 中相应浪费带宽的 28%。
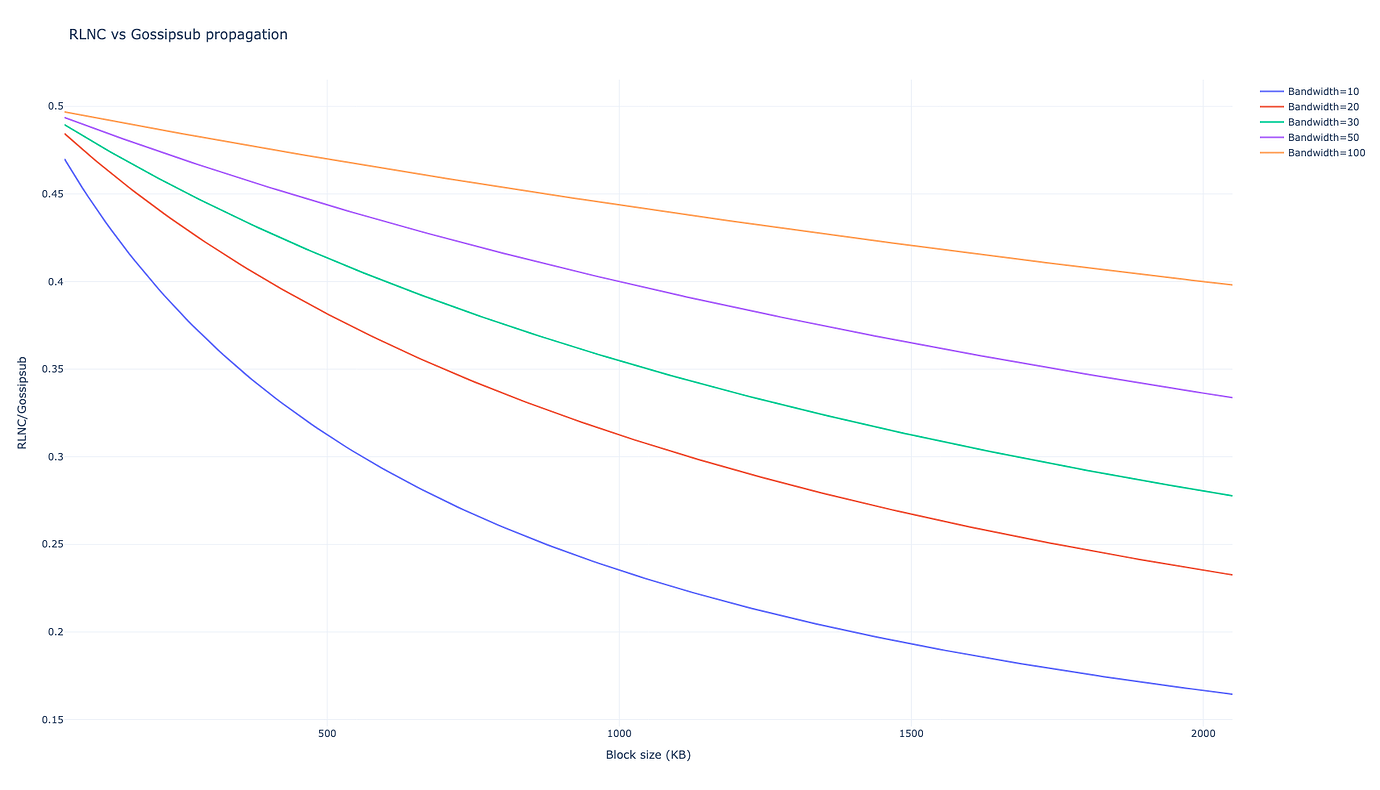
差异
对于每个节点发送的相同带宽,我们看到传播时间的不同之处在于将延迟除以 2(3 跳与 6 跳),并通过在单位时间内消耗十分之一的带宽来更快地传播块。此外,通过多余消息浪费的带宽被削减到 gossipsub 浪费消息的 28%。对于传播时间和浪费的带宽,但将每个节点发送的带宽减少一半,可以获得类似的结果。
在较低的块大小端,延迟是主要的,而 3 跳与 gossipsub 上的 6 跳是主要的区别,在较高的块大小端,带宽性能是主要的。对于更大的块大小,RLNC 中的 CPU 开销会更糟,但是考虑到传输时间的数量级,这些可以忽略不计。
 \
rlnc-gossipsub1712×982 87.7 KB
\
rlnc-gossipsub1712×982 87.7 KB
每个对等方多个块
在生产中的每个对等方一个块的方法中,具有更高带宽的节点可以选择广播到更多对等方。在节点级别,可以通过简单地广播到所有当前对等方来实现这一点,而节点运营商只需通过配置标志选择对等方的数量。另一种方法是允许节点顺序地将多个块发送到单个对等方。这些模拟的结果与上述结果完全相同,但正如预期的那样,D 要低得多。例如,对于 D=6,在每个对等方发送一个块的情况下,将永远不会广播完整块。模拟需要 10 跳才能广播完整块。当 D=10 时,跳数减少到 9。
结论、遗漏和进一步的工作
我们的结果表明,如果我们使用 RLNC 而不是当前的路由协议,那么预计块传播时间和每个节点的带宽使用率都会得到显着改善。块/blob 大小越大或每次跳跃的延迟成本越短,这些优势就越明显。实施此协议需要对当前架构进行重大更改,并且可能需要一种全新的 pubsub 机制。为了证明这一点是合理的,我们可能希望实施完整的网络堆栈以在 Shadow 下进行模拟。另一种方法是实施 Reed-Solomon 纠删码和路由,类似于我们对 Peer-DAS 所做的那样。应该很容易将上述模拟扩展到这种情况,但是 原引 已经包含了许多这样的比较。
- 原文链接: ethresear.ch/t/faster-bl...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Solana - Anza26 - Anza 137 浏览
- 影响 25.1 以前版本 Bitcoin Core 软件的漏洞披露 877 浏览
- RPC提供商性能比较 751 浏览
- 8个最佳 Hyperliquid RPC 节点供应商 1721 浏览
- Fusaka 带宽评估 1397 浏览
- RLNC内幕:P2P网络中加速广播的技术演练 939 浏览
- `IDONTWANT` 对重复消息数量的影响 - 网络 1095 浏览
- 使用 Magicblock 从零到实时 1581 浏览
- 基于RLNC的分片替代DAS概念 1167 浏览
- 比特币 - bips/bip-0144.mediawiki,位于ajtowns/bips的anyprevout 1180 浏览
- DAS和分片Blob内存池的新设计——分片 1284 浏览
- Sepolia & Hoodi 测试网的 60M Gas Limit 1578 浏览


