R1CS vs Plonk：零约束线性运算

R1CS vs Plonk: 零约束线性

Rarimo

Illia Dovhopolyi, Dmytro Zakharov

线性操作，比如那些通常在神经网络中用到的，在 CPU 上计算时非常快。然而，在 ZK 系统中，它们通常会导致大量的约束，使得它们的开销变得过于昂贵。在本文中，我们将介绍一种简单而强大的优化方法，该方法在 Bionetta 中使用，可以移除 R1CS 电路中线性操作的约束成本，使其完全免费！

线性回归示例

为了清楚地说明这一点，我们考虑一个简单的线性回归电路。我们有两个输入向量：长度为 n 的 x 和长度为 n+1 的 w。我们想要约束以下线性回归公式：

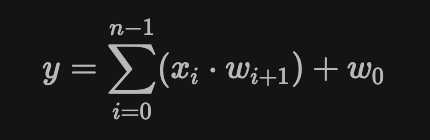
以下是当 n=100 时，这个电路在 Circom 中的样子：

pragma circom 2.1.6;

template LinearRegression(n) {
    signal input x[n];
    signal input w[n+1];

    signal output y;

    signal t[n+1];
    t[0] <== w[0];

    for (var i = 0; i < n; i++) {
        t[i+1] <== t[i] + x[i] * w[i+1];
    }

    y <== t[n];
}

component main = LinearRegression(100);

接下来，我们将这个电路编译成它的 R1CS 表示：

circom circuits/LinearRegression.circom --r1cs --O1 -o artifacts

我们可以使用以下 JS 脚本来计算电路生成的 R1CS 和 Plonk 约束的数量：

const snarkjs = require("snarkjs");
const path = require("path");

async function main() {
    const ptauFile = path.join("artifacts", "powersOfTau28_hez_final_20.ptau");
    const r1csFile = path.join("artifacts", "LinearRegression.r1cs");

    const r1cs = await snarkjs.r1cs.exportJson(r1csFile);

    console.log(`R1CS constraints: ${r1cs.nConstraints}`);

    const zkeyFile = { type: "mem" };
    await snarkjs.plonk.setup(r1csFile, ptauFile, zkeyFile, console);
}

main().catch((e) => console.error(e));

运行此脚本会得到以下结果：

> node index.js
R1CS constraints: 100
Plonk constraints: 201

这个结果并不令人惊讶。R1CS 只计算乘法的约束，产生 100 个约束。相比之下，Plonk 计算加法和乘法的 gates，产生 201 个约束。我们稍后将更详细地讨论这些差异。

电路嵌入权重

因此，当我们向模型中添加许多线性操作时，先前的方法变得非常昂贵。为了优化，我们注意到两点重要的事情：

1. Bionetta 是一个客户端证明框架，因此我们不需要隐藏模型权重。

2. 权重仅在重新训练模型时才会更改，而不是针对每个单独的证明。

这些点表明，应该将权重直接作为常量嵌入到电路中，而不是始终将它们作为 signals 传递。

你可能会想：当模型重新训练并且权重改变时会发生什么？这不会使电路失效吗？确实是这样 —— 但我们这里的假设是，开发人员可以简单地使用新权重重新编译电路并升级验证器（通常是在链上合约）。虽然这会增加某些不便，但我们相信这是一个合理的权衡，因为它显着减少了用户的证明时间。

以下是此优化在 Circom 中的外观，权重设置为常量。在这里，我们设置 w[i] = i 以进行演示。在实践中，我们将使用代码生成来插入实际训练的权重：

pragma circom 2.1.6;

template ConstantLinearRegression(n) {
        // Below, we set compile-time known weights. In the actual
        // Bionetta protocol, these values correspond to the real
        // trained values
    var w[n+1];
    for (var i = 0; i <= n; i++) {
        w[i] = i;
    }

      // The rest is essentially the same, but the weights are known
    signal input x[n];
    signal output y;

    var t = w[0];

    for (var i = 0; i < n; i++) {
        t += x[i] * w[i+1];
    }

    y <== t;
}

component main = ConstantLinearRegression(100);

让我们使用与之前相同的脚本检查我们现在有多少约束：

> node index.js
R1CS constraints: 1
Plonk constraints: 100

请注意巨大的改进：

• R1CS 线性操作变得完全免费 - 现在我们只有一个约束。

• Plonk 中的所有乘法 gates 都消失了，只剩下加法 gates。

为什么这样有效

让我们首先快速回顾一下 R1CS 和 Plonk 算术化的工作原理。假设我们有一个 witness: z=(1,z1,z2,…,zm−1)\boldsymbol{z} = (1, z_1, z_2, \dots, z_{m-1})z=(1,z1​,z2​,…,zm−1​)。

在 R1CS 中，电路由三个矩阵编码——L\mathbf{L}L, R\mathbf{R}R, 和 O\mathbf{O}O——每个矩阵的大小为 n×mn \times mn×m (其中 nnn 是约束的数量，mmm 是 witness 长度)。为了使 witness 有效，我们需要确保以下方程组 Lz∘Rz=Oz\textbf{L}\boldsymbol{z} \circ \textbf{R}\boldsymbol{z} = \textbf{O}\boldsymbol{z}Lz∘Rz=Oz 成立。

在 Plonk 中，每个约束（或“gate”）都涉及一些特定的 witness 元素 (l,r,o)(l,r,o)(l,r,o)（左、右和输出元素）。每个 gate 也有五个选择器 (qM,qL,qR,qO,qC)(q_M, q_L, q_R, q_O, q_C)(qM​,qL​,qR​,qO​,qC​)。这些选择器是常数——类似于 R1CS 矩阵中的行——它们定义了 gate 的特定操作。对于每个 gate，必须满足以下等式：

qM⋅l⋅r+qL⋅l+qR⋅r+qO⋅o+qC=0q_M\cdot l \cdot r+q_L \cdot l + q_R \cdot r + q_O \cdot o + q_C=0qM​⋅l⋅r+qL​⋅l+qR​⋅r+qO​⋅o+qC​=0

权重是 signals

假设我们有一个小的线性回归，有三个输入 (x0,x1,x2)(x_0, x_1, x_2)(x0​,x1​,x2​) 和四个权重 (w0,w1,w2,w3)(w_0, w_1, w_2, w_3)(w0​,w1​,w2​,w3​)，计算：

y=w0+w1⋅x0+w2⋅x1+w3⋅x2y = w_0 + w_1 \cdot x_0 + w_2 \cdot x_1 + w_3 \cdot x_2y=w0​+w1​⋅x0​+w2​⋅x1​+w3​⋅x2​

我们引入中间累加器元素：

t0=w0+w1⋅x0,t1=t0+w2⋅x1t_0 = w_0 + w_1 \cdot x_0, \quad t_1 = t_0 + w_2 \cdot x_1t0​=w0​+w1​⋅x0​,t1​=t0​+w2​⋅x1​

以及输出元素：

y=t1+w3⋅x2y = t_1 + w_3 \cdot x_2y=t1​+w3​⋅x2​

我们的完整 witness 向量是：

z=(1,w0,w1,w2,x0,x1,x2,t0,t1,y)\boldsymbol{z}=(1, w_0, w_1, w_2, x_0, x_1, x_2, t_0, t_1, y)z=(1,w0​,w1​,w2​,x0​,x1​,x2​,t0​,t1​,y)

很容易证明，强制执行此计算需要 3 个 R1CS 约束（或 nnn 个约束，对于 nnn 个输入）：

约束： nnn。

💡 注意：第一个约束包括信号 $w_0$ 的加法。这可以通过高斯消元法实现，Circom compiler 自动执行该方法来简化线性约束。

在 Plonk 中，我们需要为每个加法准备一个专用的 gate，因此我们引入额外的中间值：

p0=x0⋅w1,p1=x1⋅w2,p2=x2⋅w3,s0=w0+p0,s1=s0+p1,s2=s1+p2p_0 = x_0 \cdot w_1, \newline p_1 = x_1 \cdot w_2, \newline p_2 = x_2 \cdot w_3, \newline s_0 = w_0 + p_0, \newline s_1 = s_0 + p_1, \newline s_2 = s_1 + p_2p0​=x0​⋅w1​,p1​=x1​⋅w2​,p2​=x2​⋅w3​,s0​=w0​+p0​,s1​=s0​+p1​,s2​=s1​+p2​

我们添加一个最终的 复制 约束来暴露公共输出：

y=s2y = s_2y=s2​

总而言之，具有 n=3n=3n=3 个输入的线性回归电路需要 7 个 Plonk gates（通常为 2n+12n+12n+1 个 gates）：

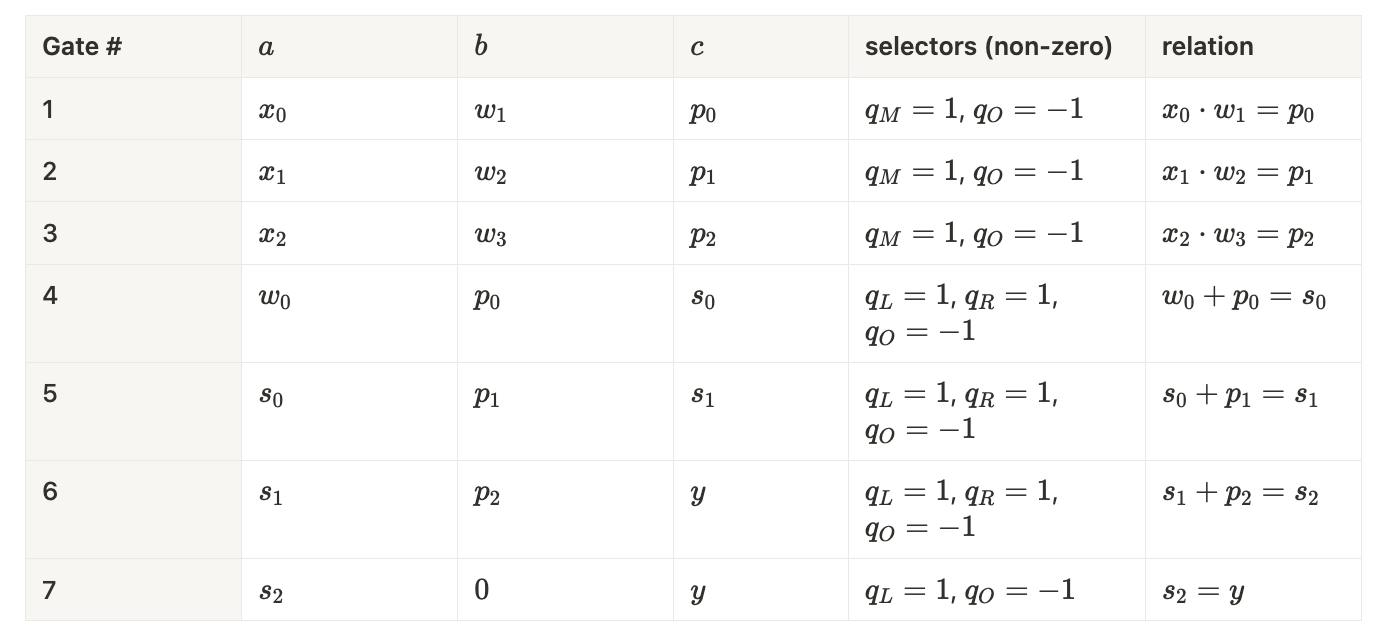
Gates: 2n+12n+12n+1.

权重是常量

假设我们将权重直接嵌入到电路中。相同的线性回归方程现在变为：

yw(x)=w0+w1⋅x0+w2⋅x1+w3⋅x2y_\mathbf{w}(\mathbf{x}) = w_0 + w_1 \cdot x_0 + w_2 \cdot x_1 + w_3 \cdot x_2yw​(x)=w0​+w1​⋅x0​+w2​⋅x1​+w3​⋅x2​

由于权重不再是 witness 的一部分，我们可以将其表示为：

z=(1,x0,x1,x2,y)\boldsymbol{z}=(1, x_0, x_1, x_2, y)z=(1,x0​,x1​,x2​,y)

这种方法的美妙之处在于，它可以将整个计算折叠成一个 R1CS 行：常量 (w0,w1,w2,w3)(w_0, w_1, w_2, w_3)(w0​,w1​,w2​,w3​) 现在位于 L\mathbf{L}L 中：

约束： 1.

在 Plonk 中，我们可以通过将权重插入到选择器中来消除所有乘法 gates，但每个加法仍然需要自己的 gate。对于 n=3n=3n=3 个输入，电路使用 3 个 gates（或通常为 nnn 个 gates）：

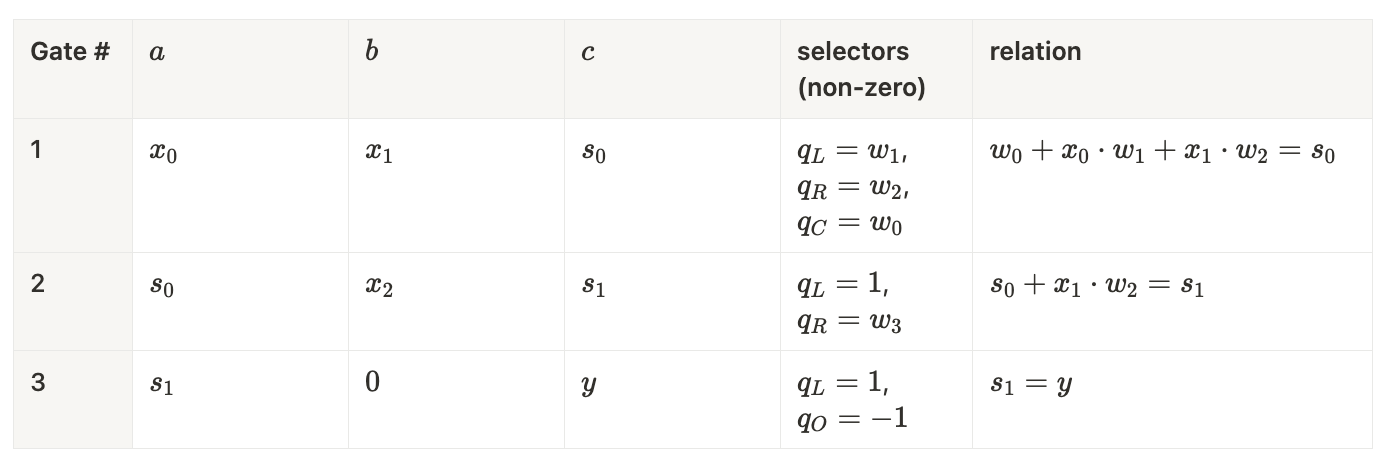
Gates: nnn.

基准测试

为了对这种优化进行基准测试，我们实现了一个特殊的 MultiLinearRegression 电路，并测量了两种情况下的证明时间：一种是将权重作为 signals，另一种是将权重嵌入为常量。

这是这个电路在 Circom 中的样子：

pragma circom 2.1.6;

template ConstantMultiLinearRegression(n) {
    var w[n][n+1];
    for (var i = 0; i < n; i++) {
        for (var j = 0; j <= n; j++) {
            w[i][j] = i * n + j;
        }
    }
    signal input x[n];

    signal output out[n];

    for (var i = 0; i < n; i++) {
        var t = w[i][0];

        for (var j = 0; j < n; j++) {
            t += w[i][j+1] * x[j];
        }

        out[i] <== t;
    }
}

component main = ConstantMultiLinearRegression(100);

这是 Noir 中的等效实现：

global W: [[Field; 101]; 100] = [...]

mod consts;

fn const_multi_linear_regression<let N: u32>(x: [Field; N]) -> [Field; N] {
    let mut out = [0; N];

    for i in 0..N {
        let mut t = consts::W[i][0];

        for j in 0..N {
            t += consts::W[i][j+1] * x[j];
        }

        out[i] = t;
    }

    out
}

fn main(x: [Field; 100]) -> pub [Field; 100] {
    const_multi_linear_regression::<100>(x)
}

我们记录了 SnarkJS、RapidSnark 和 Aztec Barretenberg 实现的证明时间：

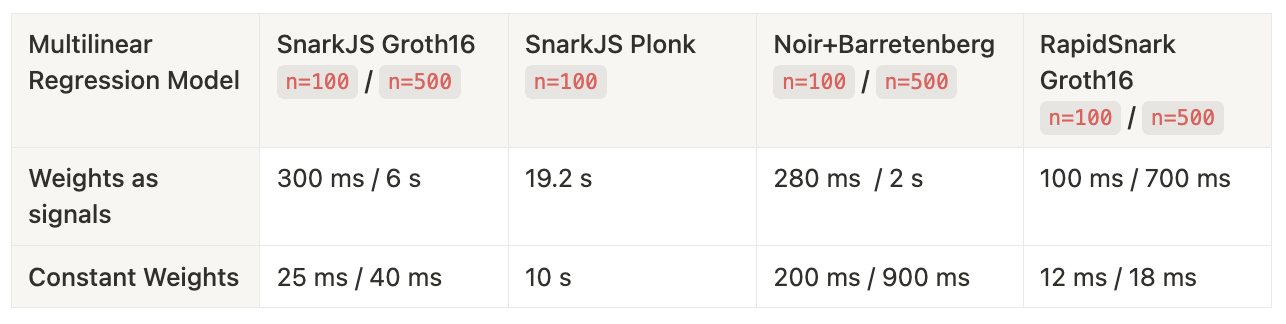
如演示所示，将权重作为常量嵌入可以显着提高 R1CS 和 Plonk 系统的证明时间。由于约束的显着减少，R1CS 系统明显更快。有趣的是，将参数 n（表示线性回归的大小）从 100 增加到 500 对基于 R1CS 的证明系统的证明时间影响不大。

结论

在R1CS电路中，将权重直接嵌入到电路中使线性运算完全免费。这是我们选择首先在我们的客户端证明框架 Bionetta 中支持基于 R1CS 的证明系统的主要原因之一。结合我们即将推出的非线性运算的优化（请参阅下一篇关于 UltraGroth 的文章），这使得 Bionetta 异常高效：即使是大型神经网络模型（例如 zkLiveness 模型）也大致适合 10 万个约束，并且可以非常快速地证明。

• 原文链接： mirror.xyz/0x90699B5A52B...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～