塑造现代零知识证明的10篇必读论文 - ZKSECURITY

零知识证明在近 40 年里取得了显著的进步，达到了前所未有的复杂性和效率水平。如今，每天都有新的论文和项目涌现，建立在丰富的思想和创新基础之上。

好奇这一切是如何开始的吗？ 在这篇文章中，我们将深入探讨零知识证明的历史，探索 10 篇塑造了我们今天所知的该领域的里程碑式论文。

#1 - 起源

Goldwasser, Micali, Rackoff - 交互式证明系统的知识复杂度 (1985) 1

我们的第一个里程碑将我们带回到 1985 年，那时一切都开始了！这项工作引入了许多术语和基础概念，这些术语和概念至今仍是零知识证明的核心。

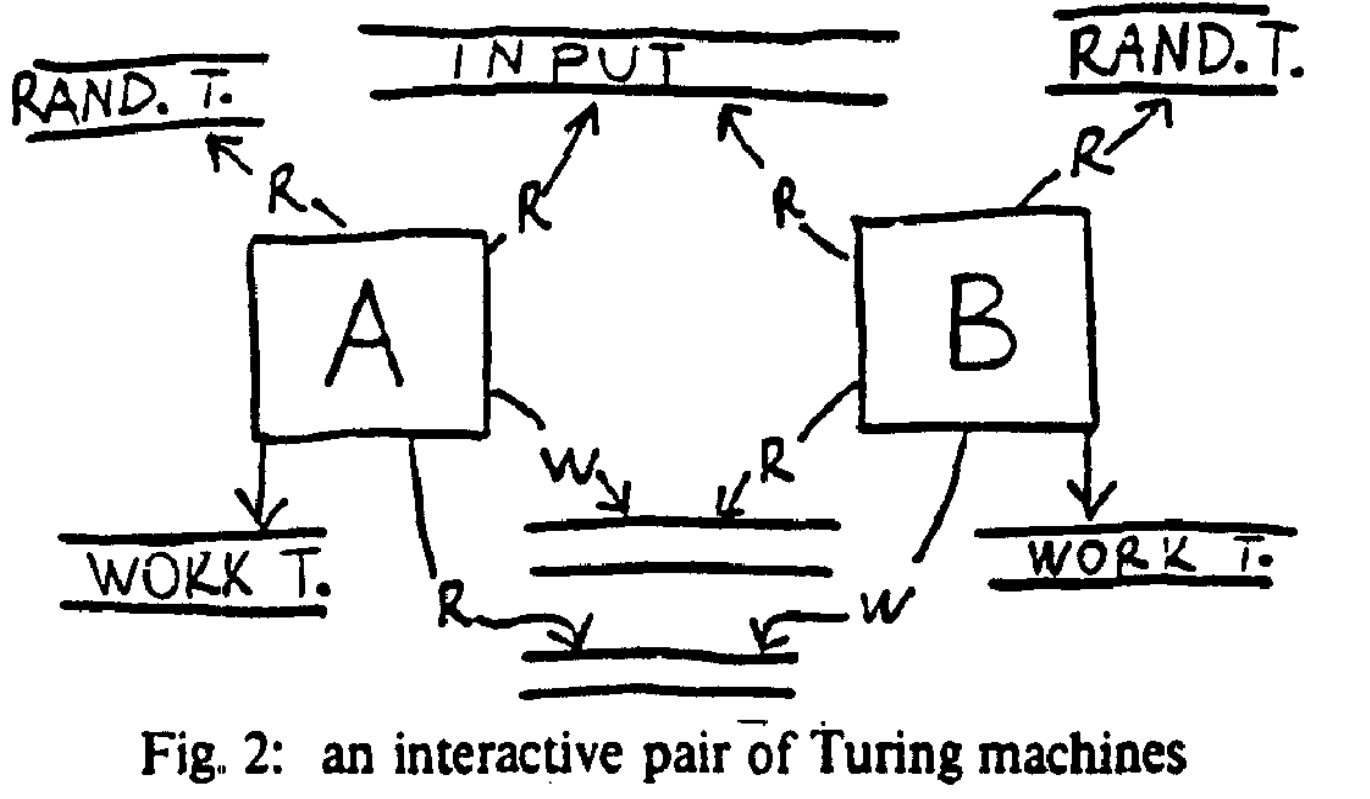
首先，该论文定义了一个证明系统，该系统被建模为一个双方协议，涉及两个概率图灵机：证明者和验证者。形式语言 L 的证明系统的目标是使证明者能够说服验证者给定的输入 x 属于 L。在大多数早期工作中，证明者的计算能力不受限制，而验证者仅限于多项式时间计算。在交互结束时，验证者输出“接受”或“拒绝”。

一个证明系统具有两个主要属性：完备性（如果 x∈L，则验证者以高概率接受）和可靠性（如果证明者试图作弊且 x∉L，则验证者以高概率拒绝）。一个简单的证明系统包括证明者简单地将 witness w 发送给验证者。但是，这种方法会向验证者揭示有关 witness 的信息或知识。 为了形式化这个概念，该论文引入了知识复杂度：KC(f(x)) 代表一类语言，这些语言允许一个证明系统，其中证明者最多交流关于其输入 x 的 f(n) 位知识。

是否存在 KC(0) 中的语言，这意味着它们允许零知识证明系统？值得注意的是，确实存在！该论文提出了一个著名的例子，涉及二次剩余性的证明系统，其中证明者可以使验证者确信，给定的数字 x 是复合数字 n 的二次剩余，而无需揭示关于 x 的任何其他知识。

#2 - 第一个应用

Fiat, Shamir - 如何证明你自己：识别和签名问题的实用解决方案 (1986) 2

这篇由 Fiat 和 Shamir 撰写的论文，在零知识证明的基础性工作发表仅仅一年后，介绍了这些概念的第一个实际应用。他们提出了两个协议：一个交互式的识别方案和一个非交互式的签名方案。 两者之间的关键区别在于，在识别方案中，第三方可以通过制作有效的 transcript 让自己相信一个错误的陈述。 在签名协议中，即使是不诚实的证明者也无法让自己相信一个错误的陈述，从而使签名不可伪造。

识别方案将二次剩余性证明系统应用为交互式协议，其中验证者发送随机 challenge，而证明者做出相应的响应。签名方案通过用对哈希函数的调用替换验证者的 challenge 来修改此方案。

作者的名字听起来是否很熟悉？这是现在广为人知的强大通用技术Fiat-Shamir 启发式的第一个实例。它通过用对随机预言机（在实践中，是密码学哈希函数）的查询替换验证者的 challenge，从而能够将任何公共 coin 交互式证明系统转换为非交互式证明系统。

#3 - 我们究竟能证明什么？

Goldreich, Micali, Wigderson - 如何在零知识中证明所有 NP 陈述以及密码协议设计的方法论 (1987) 3

这篇 1986 年的论文给出了一个显著的结果：NP 中的每种语言都允许零知识证明系统。这非常重要，因为它意味着我们可以证明任何可在多项式时间内验证的陈述的真实性，而无需揭示其他信息。作者通过为图 3 着色性提供证明系统来证明这一点，该问题确定图的节点是否可以用三种颜色着色，以使没有两个相邻的节点共享相同的颜色。此外，该证明仅假设概率加密的存在。

证明的直觉如下：在每一轮中，

• 证明者选择三种颜色的随机排列，
• 证明者提交每个节点的排列颜色，
• 验证者查询两个相邻的节点并要求它们的颜色，
• 证明者通过揭示被查询节点的颜色来打开该承诺。
• 如果颜色匹配，则验证者立即拒绝。

通过运行此协议多项式次，验证者确信证明者以高概率知道有效的 3 着色，而不会学习任何信息，因为打开的颜色在每个步骤都被随机化了！

同样值得注意的是这一系列工作中的另外两篇论文：所有可证明的东西都可以在零知识中证明 4，它表明 IP 中的每种语言都具有零知识证明系统，以及 IP = PSPACE 5，表明 IP 与 PSPACE 一样强大。

#4 - PCPs 和简洁非交互式证明的起源

Micali - 计算可靠的证明 (2000) 6

这篇 Micali 于 2000 年发表的论文是对零知识证明历史的重要贡献。它甚至可以被认为是第一个 SNARK 构造，尽管 SNARK 一词尚未被创造出来！

Micali 的构造将任何概率可检查证明（PCP）转换为简洁且非交互式的证明。PCP 是可以通过仅读取几个位来验证的证明，而一个关键结果，被称为 PCP 定理 7，表明 NP 中的每种语言都具有 PCP，该 PCP 可以通过仅从证明中读取一个常量的位数来验证！

Micali 的构造使用 Merkle 树，如下所示：

• 证明者为证明构造一棵 Merkle 树，并将根发送给验证者，
• 验证者查询他们希望检查的特定位，
• 证明者为这些位提供身份验证路径，并且验证者验证这些路径。

通过直接应用 Fiat-Shamir 启发式，可以使该构造非交互式（此转换的一个交互式版本归功于 Kilian 8）。 该论文还侧重于计算效率：实际上，验证者不需要接收整个证明，而只需要少量位和身份验证路径，这使得证明变得简洁。 该系统的主要缺点是 PCP 构造不切实际，这是开发交互式预言机证明（IOP）的动机，IOP 是 PCP 的概括，可以产生实际的论证。

#5 - 双重高效的 IPs

Goldwasser, Kalai, Rothblum - 委托计算：麻瓜的交互式证明 (2015) 9

本文强烈关注效率，并介绍了广为人知的 GKR 协议，这是一种用于算术电路可计算语言的公共 coin 交互式协议。值得注意的是，验证者和證明者都在多项式时间内运行，从而使其成为一种双重高效的交互式证明。

该协议首先由证明者和验证者就扇入为 2 的算术电路达成一致。然后，证明者发送给定输入值的电路的声明输出。该协议通过逐层检查此电路来进行，从输出层开始并朝着输入层移动。每个步骤都将当前层的声明减少为关于上一层的声明，直到验证者到达输入，在该输入处，他们可以检查其是否与原始输入匹配。

在每个步骤中，使用的主要原语是 sum-check 协议 10，这是一种交互式证明，使证明者能够使验证者确信 v 变量多项式 g 的值之和，验证者可以通过预言机访问该多项式，在布尔超立方体上： H=∑b1∈0,1∑b2∈0,1…∑bv∈0,1g(b1,b2,…,bv)

由于其效率和简单性，sum-check 和 GKR 协议都在实践中得到广泛使用。有关更多说明，可以在 Thaler 的注释中找到这些协议的替代概述 11。

#6 - 第一个实用的 SNARK

Gennaro, Gentry, Parno, Raykova - 没有 PCP 的二次跨度程序和简洁的 NIZK (2013) 12

现在，我们跳到一篇介绍最早的实用 SNARK 构造之一的论文！ 这项工作标志着旨在创建不依赖于低效 PCP 定理的 SNARK 的一系列研究的顶峰。虽然 PCP 定理提供了一个理论上的 SNARK 构造，但对于实际应用来说太慢了，因此研究人员试图找到更有效的替代方案。 例如，Groth 在 2010 年提出了一个基于双线性群和配对的非交互式论证系统 13，尽管它需要证明者的二次时间。但是，该论文实现了线性证明者时间，这是实际使用的重大改进。

这项工作为其他重要协议（例如 Pinocchio 协议 14）以及最终众所周知的 Groth16 15 证明系统铺平了道路。该论文还介绍了二次跨度程序和二次算术程序，这些是这些系统中仍使用的基本构造。

这些构造的一个显着缺点是需要可信设置，这意味着公共参考字符串生成阶段会产生秘密信息（通常称为有毒废物），如果不正确销毁，则可用于创建虚假证明。此外，此设置不是通用的，这意味着每个要支持的电路都需要一个新的设置。尽管存在这些限制，但生成的证明大小仍然是不同构造中最小的，使其成为各种应用的热门选择。

还值得一提的是 Zerocash 16 的第一个版本，这是一个利用 zk-SNARK 的早期且有影响力的区块链应用，它建立在这些系统之上。

#7 - PlonK SNARK

Gabizon, Williamson, Ciobotaru - PlonK：用于普世非交互式知识参数的基于 Lagrange 基的置换 (2019) 17

这篇 2019 年发表的有影响力的论文介绍了 PlonK SNARK，该系统基于多项式交互式预言机证明（IOP），这意味着验证者可以通过预言机访问某些多项式，并且可以在选定的点评估它们。该系统使用各种多项式组件来证明关于多项式的陈述，其中最著名的是大乘积参数，允许证明者证明域上评估的乘积为 1。使用此方法，我们可以构造一个置换参数来证明两个序列是彼此的置换。 使用这些组件，证明者可以为任何算术电路构造证明，并且验证者可以以非交互方式验证它。

在实践中，预言机访问是通过多项式承诺方案（PCS）实现的，该方案允许证明者：

• 承诺一个多项式，以及
• 提供在特定点评估的开放。

这允许验证者在任何点查询该多项式并验证 IOP 的关系。论文中建议的 PCS 是 KZG 承诺方案 18，它既高效又实用。KZG 使证明者可以将多项式承诺为单个群元素，并且验证者可以通过计算几个椭圆曲线配对来确认开放。虽然 KZG 需要可信设置，但它是通用的，并且可以在设置后用于任何电路。但是，PlonK 可以与其他 PCS 方案组合，使其适用于透明论证系统。

此外，PlonK 中的置换参数激发了查找参数。查找参数使证明者可以证明一个序列的所有元素都包含在另一个序列中，这对于 zkVM 架构非常有用。查找参数允许将 witness 分解为更小的 trace，并证明它们之间的查找关系，从而使复杂的证明更加有效。

#8 - STARKs

Ben-Sasson, Bentov, Horesh, Riabzev - 可扩展、透明且后量子安全的计算完整性 (2018) 19

本文介绍了 STARK 证明系统，它是另一个流行的证明系统，它基于 FRI 20，这是一种用于 Reed-Solomon 码的邻近测试的 IOP 协议。 在 STARK 中，证明者通过在域上多项式评估的基础上构造 Merkle 树来承诺多项式。 由于承诺的值最初是未知的，因此验证者使用 FRI 来确认这些评估形成一个足够低阶的有效多项式。 此协议还可以用作多项式承诺方案，允许验证者检查承诺的多项式在任何点的评估。

STARK 最引人注目的功能之一是它们仅依赖于密码学抗碰撞哈希函数，而不是其他密码学假设，例如离散对数问题。 这使得 STARK 具有潜在的后量子安全性，因为即使面对量子攻击，抗碰撞哈希函数也被广泛认为是安全的。 此外，STARK 是透明的，即它们不需要任何可信设置。 它们也是通用的，这意味着它们不限于特定的电路，从而为各种应用提供了灵活性。

#9 - 递归

Valiant - 增量可验证计算或知识证明意味着时间/空间效率。 (2008) 21

多年来出现的一个重要概念是递归，简单来说，这意味着可以使用一个证明来证明另一个证明的正确性。本文提出的场景涉及一个证明者想要证明一个可能很长的计算结果的正确性。给定一台图灵机，我们可以证明状态转换函数的单个步骤的正确性，但这还不够；我们想证明整个计算的正确性，该计算由状态转换的序列组成。

增量可验证计算（IVC）背后的思想如下：假设我们可以证明从 S1 到 S2 的单个状态转换是正确的。然后我们可以将两个证明合并为一个：证明者表明他们知道两个有效的证明：

• π 用于从 S1 到 S2 的状态转换，以及
• π′ 用于从 S2 到 S3 的状态转换。

组合后的证明将使验证者确信从 S1 到 S3 的转换是正确的。可以针对任意数量的步骤重复此过程，从而使我们可以将任意长的计算压缩为单个证明（更具体地说，是多项式长的计算）。

重要的是要注意，此构造依赖于两个关键假设：

• 证明系统的知识可靠性：证明者不仅必须证明单个状态转换存在证明，还必须证明他们知道这些证明。直觉是，通过归纳法的知识可提取性，我们可以提取所有单个状态转换证明。
• 实践中的哈希函数是随机预言机：这是一个更强的假设，但是对于验证聚合证明中子证明的正确性是必要的。

尽管此构造在理论上很强大，但实际上应用起来成本很高。为了解决这个问题，已经提出了新的方法来提高效率。其中之一是使用 folding schemes 22，它放宽了假设并避免了对递归 SNARK 验证的需求。Folding 背后的思想是，给定两个证明 π 和 π′，我们可以将它们“折叠”成单个证明 π″。验证者确信，如果折叠后的实例是可满足的，那么原始实例也是可满足的。

#10 - 通过 zkVM 进行可验证计算

Ben-Sasson, Chiesa, Tromer, Virza - 用于冯·诺依曼架构的简洁非交互式零知识 (2014) 23

最后一篇论文讨论了零知识虚拟机（zkVM）的第一个实际构造，零知识虚拟机是一种能够执行任意程序并为这些计算的正确性生成证明的虚拟机。描述的机器遵循冯·诺依曼架构，这意味着程序和数据都存储在同一内存中。大多数现代 CPU 都基于这种范例运行，因此，从理论上讲，可以在经典计算机上运行的任何程序也可以在这种架构上运行。

该论文介绍了一种名为 vnTinyRAM 的 RISC 架构，并提出了一个移植到目标指令集的 C 编译器。证明系统旨在验证程序执行的正确性，最多可以达到固定数量的步骤。基本思想是将电路构造为重复的状态转换函数，展开直到达到指令计数限制。

如今，zkVM 越来越受欢迎。它们的主要优势之一是用户可以用高级编程语言编写程序并使用它们来生成证明。与手动编写电路相比，这提供了一个显着的优势，因为许多标准算法和数据结构已经在这些高级语言中定义。此外，开发人员可以重复使用熟悉的计算模型，从而大大减少了与使用零知识证明相关的学习曲线。

还值得注意的是，许多 zk-rollup 都基于此模型。例如，支持以太坊虚拟机（EVM）执行的 zk-rollup 使用 zkVM 来证明 EVM 正确执行。

最后，该论文介绍了其自身的架构，该架构经过优化，可用于零知识证明系统。zk 友好架构的另一个流行示例是 Cairo CPU architecture 24，这是一个图灵完备的 CPU，经过优化可以使用 STARK 进行证明。

1. Goldwasser, S., Micali, S., & Rackoff, C. (1985). 交互式证明系统的知识复杂度。( link) ↩︎

2. Fiat, A., & Shamir, A. (1986). 如何证明你自己：识别和签名问题的实用解决方案。( link) ↩︎

3. Goldreich, O., Micali, S., & Wigderson, A. (1987). 如何在零知识中证明所有 NP 陈述以及密码协议设计的方法论。( link) ↩︎

4. Ben-Or, M., Goldreich, O., Goldwasser, S., Håstad, J., Kilian, J., Micali, S., & Rogaway, P. (1990). 所有可证明的东西都可以在零知识中证明。( link) ↩︎

5. Shamir, A. (1992). IP=PSPACE。( link) ↩︎

6. Micali, S. (2000). 计算可靠的证明。( link) ↩︎

7. Cook, S. A. (1971). 证明验证和近似问题的硬度。( link) ↩︎

8. Kilian, J. (1992, July). 关于高效零知识证明和论证的说明。( link) ↩︎

9. Goldwasser, S., Kalai, Y. T., & Rothblum, G. N. (2015). 委托计算：麻瓜的交互式证明。( link, 另请参阅 Justin Thaler 的这份 note) ↩︎

10. Lund, C., Fortnow, L., Karloff, H., & Nisan, N. (1992). 交互式证明系统的代数方法。( link) ↩︎

11. Thaler, J. (2015). 关于 GKR 协议的说明。( link) ↩︎

12. Gennaro, R., Gentry, C., Parno, B., & Raykova, M. (2013). 没有 PCP 的二次跨度程序和简洁的 NIZK。( link) ↩︎

13. Groth, J. (2010). 基于配对的短非交互式零知识参数。( link) ↩︎

14. Parno, B., Howell, J., Gentry, C., & Raykova, M. (2016). Pinocchio：几乎实用的可验证计算。( link) ↩︎

15. Groth, J. (2016). 关于基于配对的非交互式参数的大小。( link) ↩︎

16. Sasson, E. B., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., & Virza, M. (2014). Zerocash：来自比特币的去中心化匿名支付。( link) ↩︎

17. Gabizon, A., Williamson, Z. J., & Ciobotaru, O. (2019). Plonk：用于普世非交互式知识参数的基于拉格朗日基的置换。( link) ↩︎

18. Kate, A., Zaverucha, G. M., & Goldberg, I. (2010). 多项式的恒定大小承诺及其应用。( link) ↩︎

19. Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). 可扩展、透明且后量子安全的计算完整性。( link) ↩︎

20. Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). 快速里德-所罗门交互式预言机邻近证明。( link) ↩︎

21. Valiant, P. (2008). 增量可验证计算或知识证明意味着时间/空间效率。( link) ↩︎

22. Kothapalli, A., Setty, S., & Tzialla, I. (2022, August). Nova：来自 Folding Schemes 的递归零知识参数。( link) ↩︎

23. Ben-Sasson, E., Chiesa, A., Tromer, E., & Virza, M. (2014). 用于冯·诺依曼架构的简洁非交互式零知识。( link) ↩︎

24. Goldberg, L., Papini, S., & Riabzev, M. (2021). Cairo——一种图灵完备的 STARK 友好 CPU 架构。( link) ↩︎

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～