零知识证明 - 深入理解powersoftau
- Star Li
- 发布于 2020-12-24 10:07
- 阅读 5226
powersoftau,采用MPC以及随机Beacon,完成可信设置。通过POK算法实现可验证的密钥对,并建立和上一个参与方计算结果的绑定。参与可信设置的人数可扩展,并且参与方只需要按照顺序一个个的进行指定的计算即可。协调方在接收到某个参与方的计算后,验证后,发送给下一个参与方。
学习区块链技术的小伙伴不知道有没有同样的体验,每天脑袋都在膨胀,每天都有很多新鲜的知识需要学习总结。最近有些空闲时间看了看powersoftau。了解零知识证明算法的小伙伴的都知道,在利用某些零知识证明算法之前,需要可信设置。Groth16算法针对不同的电路需要单独的可信设置,生成CRS。PLONK算法是Univeral的零知识证明算法,针对不同的电路,在电路规模不超过一定范围的情况下,只需要一次可信设置。如何让多个参与方安全地进行可信设置,生成零知识证明的可信参数,就是powersoftau解决的事情。
powersoftau,采用MPC以及随机Beacon,完成可信设置。
理论基础
目前开源的powersoftau采用的是2017发表的论文:
Scalable Multi-party Computation for zk-SNARK Parameters in the Random Beacon Model
参与方/协调方
整个可信设置由参与方(player)以及协调方(coordinator)组成。协调方将前一个参与方生成的数据发送给下一个参与方。在所有参与方计算完成后,协调方再通过公开随机Beacon参与计算生成最后的参数。
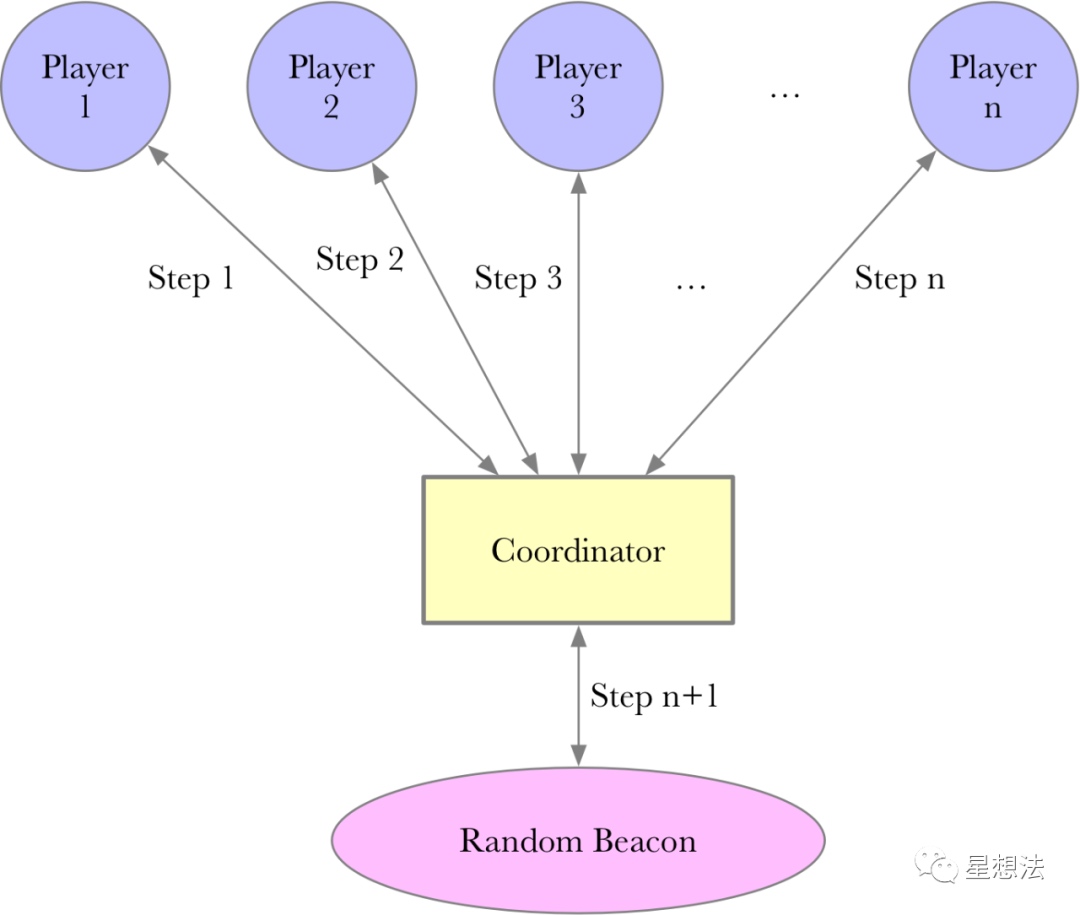
协调方,并不需要可信第三方,因为协调方通过公开随机Beacon生成的参数是可以验证的。所谓的公开随机Beacon,是在某个时间点之前并不知道的随机性数据,并且在同一个时间点后,所有人都可以验证随机数据。
Phase1/Pahse2
论文的第二章给出了整个协议的大体思路。假设Alice和Bob是两个参与方,整个协议逻辑上分成两步:Phase1和Phase2。

Phase1计算出某个多项式项的tau对应的值。Phase2计算出整个多项式对应的值。注意这些值都是有限域上的点。简单的说,Phase1提供单个项的MPC的计算结果,Phase2提供多项组合的MPC的计算结果。Phase1和Phase2计算流程类似,参与方一个个的接着做。整个协议涉及两个基本计算:CONSISTENT和POK。
CONSISTENT
CONSISTENT用来检查两个配对函数的结果是否相等。

检查A,B,C是否满足e(A,B) = e(C1,C2),记为:consistent(A-B; C)。
POK
POK - proof of knowledge。

参数alpha是知识(knowledge)。为了证明知道知识alpha,先计算出r(alpha对应的G1上的点和公共字符串v),并生成G2上的点。通过提供alpha在G1上的点以及alpha*r,可以证明知道知识alpha。证明可以通过配对函数进行验证。
协议逻辑
论文的第四章给出了整个协议的定义。电路被抽象成两个结构:一个结构是计算过程只有乘除的电路部分,一个结构是组合部分。
对一个电路,证明的计算过程如下:

1(a) - 对电路中的每个输入,进行POK的证明。注意v是上一层的结果计算生成。
1(b) - 在上一参与者计算结果的基础上,计算当前参与者的计算结果。其中M是电路的多项式函数。
2 - 应用随机Beacon
相对于计算过程,验证过程也比较清晰:

验证POK证明,验证M的计算是否正确。
论文的第6/7章,详细给出了Groth16算法参数的生成过程。感兴趣的小伙伴,可以自行查看。
源代码分析
powersoftau在github上有多个项目,大同小异。以matter labs的代码为例,分析一下代码逻辑。
https://github.com/matter-labs/powersoftau
这个项目实现Groth16算法的可信设置,支持BN256以及BLS12_381曲线。特别注意的是,这个项目只实现了Phase1,组合的部分(Phase2)这个项目并不涉及。
代码结构
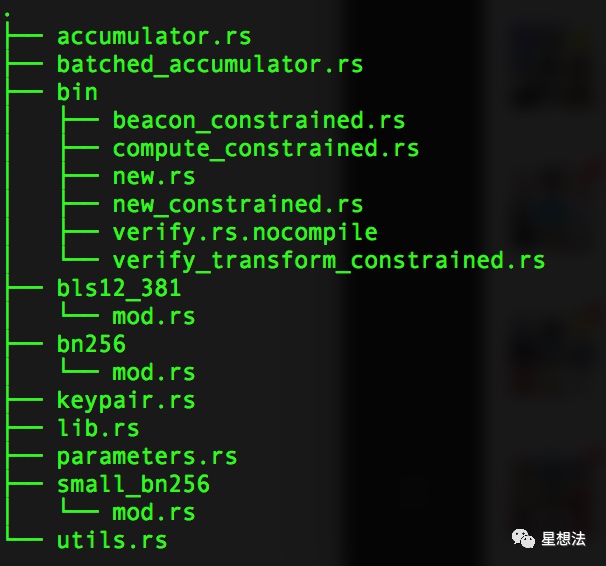
accumulator.rs和batched_accumulator.rs顾名思义,累加器,多个参与者的计算结果的“累加”。bin目录下实现多个程序,实现计算(包括随机Beacon的应用计算),验证计算等等。parameters.rs是参数配置。bn256/small_bn256/bls12_381是对应曲线的参数配置。keypair.rs实现了公钥和私钥的管理。utils.rs实现了一些辅助函数。先从keypair说起。
keypair
keypair实现PublicKey和PrivateKey密钥对。私钥比较直接,包括tau,alpha以及beta:
pub struct PrivateKey {
pub tau: E::Fr,
pub alpha: E::Fr,
pub beta: E::Fr
}私钥是随机生成的。公钥相对复杂一些:
pub struct PublicKey {
pub tau_g1: (E::G1Affine, E::G1Affine),
pub alpha_g1: (E::G1Affine, E::G1Affine),
pub beta_g1: (E::G1Affine, E::G1Affine),
pub tau_g2: E::G2Affine,
pub alpha_g2: E::G2Affine,
pub beta_g2: E::G2Affine
}针对tau,alpha以及beta,生成G1/G2对应的点。三者的计算方式一致。详细看一下tau对应的公钥的生成过程:
let mut op = |x: E::Fr, personalization: u8| {
// Sample random g^s
let g1_s = E::G1::rand(rng).into_affine();
// Compute g^{s*x}
let g1_s_x = g1_s.mul(x).into_affine();
// Compute BLAKE2b(personalization | transcript | g^s | g^{s*x})
let h: generic_array::GenericArray<u8, U64> = {
let mut h = Blake2b::default();
h.input(&[personalization]);
h.input(digest);
h.input(g1_s.into_uncompressed().as_ref());
h.input(g1_s_x.into_uncompressed().as_ref());
h.result()
};
// Hash into G2 as g^{s'}
let g2_s: E::G2Affine = hash_to_g2::<E>(h.as_ref()).into_affine();
// Compute g^{s'*x}
let g2_s_x = g2_s.mul(x).into_affine();
((g1_s, g1_s_x), g2_s_x)
};g1_s是在G1随机生成的点,g1_s_x是x g1_s。g2_s的生成依赖一个digest信息和g1_s的点。也就是说,在知道g1_s和g1_s_x的点以及digest信息的情况下,所有人都可以推算出来。g2_s_x是x g_s。
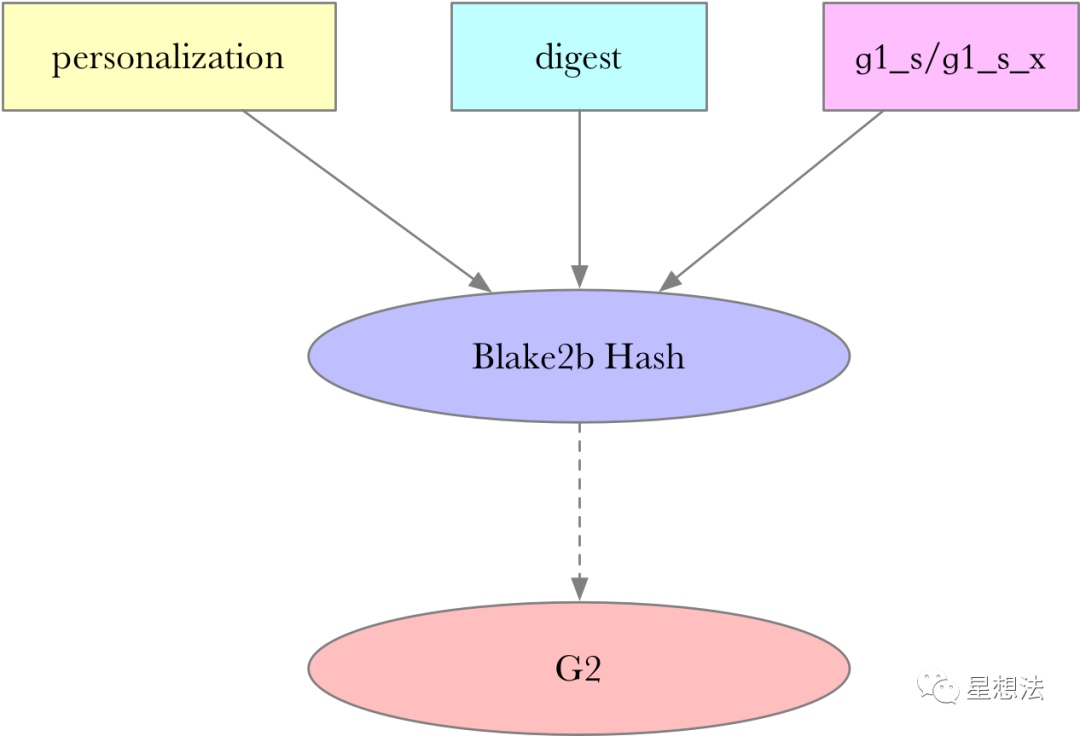
其中digest信息是前一个参与者计算结果的hash,具体计算在bin代码解释时详细描述。因为在知道g1_s,g1_s_x和digest的情况下,g2_s可以推算出来。所以,公钥信息只要这三个点就足够:((g1_s, g1_s_x), g2_s_x)。
accumulator
Accumulator负责将多个参与方生成的“参数”信息“累加”起来。所有的参数信息都清晰的描述在注释中:
pub struct Accumulator<E: Engine, P: PowersOfTauParameters> {
/// tau^0, tau^1, tau^2, ..., tau^{TAU_POWERS_G1_LENGTH - 1}
pub tau_powers_g1: Vec<E::G1Affine>,
/// tau^0, tau^1, tau^2, ..., tau^{TAU_POWERS_LENGTH - 1}
pub tau_powers_g2: Vec<E::G2Affine>,
/// alpha * tau^0, alpha * tau^1, alpha * tau^2, ..., alpha * tau^{TAU_POWERS_LENGTH - 1}
pub alpha_tau_powers_g1: Vec<E::G1Affine>,
/// beta * tau^0, beta * tau^1, beta * tau^2, ..., beta * tau^{TAU_POWERS_LENGTH - 1}
pub beta_tau_powers_g1: Vec<E::G1Affine>,
/// beta
pub beta_g2: E::G2Affine,
/// Keep parameters here
pub parameters: P
}注意tau在G1和G2上的点的个数不一样,分别是TAU_POWERS_G1_LENGTH和TAU_POWERS_LENGTH。这两个宏的计算方式定义在parameters.rs中:
const TAU_POWERS_LENGTH: usize = (1 << Self::REQUIRED_POWER)
const TAU_POWERS_G1_LENGTH: usize = (Self::TAU_POWERS_LENGTH << 1) - 1;Accumulator主要提供了两个函数transform和verify_transform函数。transform函数在现有Accumulator的基础上叠加目前的PrivateKey的计算。
pub fn transform(&mut self, key: &PrivateKey<E>)
{
...
batch_exp::<E, _>(&mut self.tau_powers_g1, &taupowers[0..], None);
batch_exp::<E, _>(&mut self.tau_powers_g2, &taupowers[0..P::TAU_POWERS_LENGTH], None);
batch_exp::<E, _>(&mut self.alpha_tau_powers_g1, &taupowers[0..P::TAU_POWERS_LENGTH], Some(&key.alpha));
batch_exp::<E, _>(&mut self.beta_tau_powers_g1, &taupowers[0..P::TAU_POWERS_LENGTH], Some(&key.beta));
self.beta_g2 = self.beta_g2.mul(key.beta).into_affine();
...
}其中taupowers是tau^0, tau^1...tau^(TAU_POWERS_G1_LENGTH)的计算结果。
verify_transform验证transform的计算是否正确。验证需要提供需要验证的计算之前的Accmulator和之后的Accumlator,公钥信息以及digest信息。以tau的计算为例,解释相关逻辑:
pub fn verify_transform<E: Engine, P: PowersOfTauParameters>(before: &Accumulator<E, P>, after: &Accumulator<E, P>, key: &PublicKey<E>, digest: &[u8]) -> bool在计算出g2_s的基础上(包括g1_s,g1_s_x和digest信息),首先验证公钥信息是否正确:
if !same_ratio(key.tau_g1, (tau_g2_s, key.tau_g2)) {验证公钥信息,就是POK的验证过程。
接着检查tau^0是否为1:
// Check the correctness of the generators for tau powers
if after.tau_powers_g1[0] != E::G1Affine::one() {
return false;
}
if after.tau_powers_g2[0] != E::G2Affine::one() {
return false;
}验证tau的计算是否正确:
if !same_ratio((before.tau_powers_g1[1], after.tau_powers_g1[1]), (tau_g2_s, key.tau_g2)) {验证tau的其他幂次对应的点计算是否正确:
if !same_ratio(power_pairs(&after.tau_powers_g1), (after.tau_powers_g2[0], after.tau_powers_g2[1])) {
return false;
}
if !same_ratio(power_pairs(&after.tau_powers_g2), (after.tau_powers_g1[0], after.tau_powers_g1[1])) {
return false;
}power_pairs是有个有意思的设计。为了验证所有的幂次对应的点计算是否正确,power_pairs将所有的幂次对应的点乘以单独的随机数,并错位累加。一次验证就能保证多个点是幂次递增关系。
bin
bin实现整个可信设置的协议,包括四种操作:1/new(创建初始的Accumulator) 2/ compute (贡献一次参数计算) 3/ verify (验证一次参加计算) 4/ beacon(贡献随机beacon的参数计算)。
重点梳理一下compute和verify的逻辑,其他逻辑类似。逻辑分别实现在compute_constrainted.rs和verify_transform_constrainted.rs。
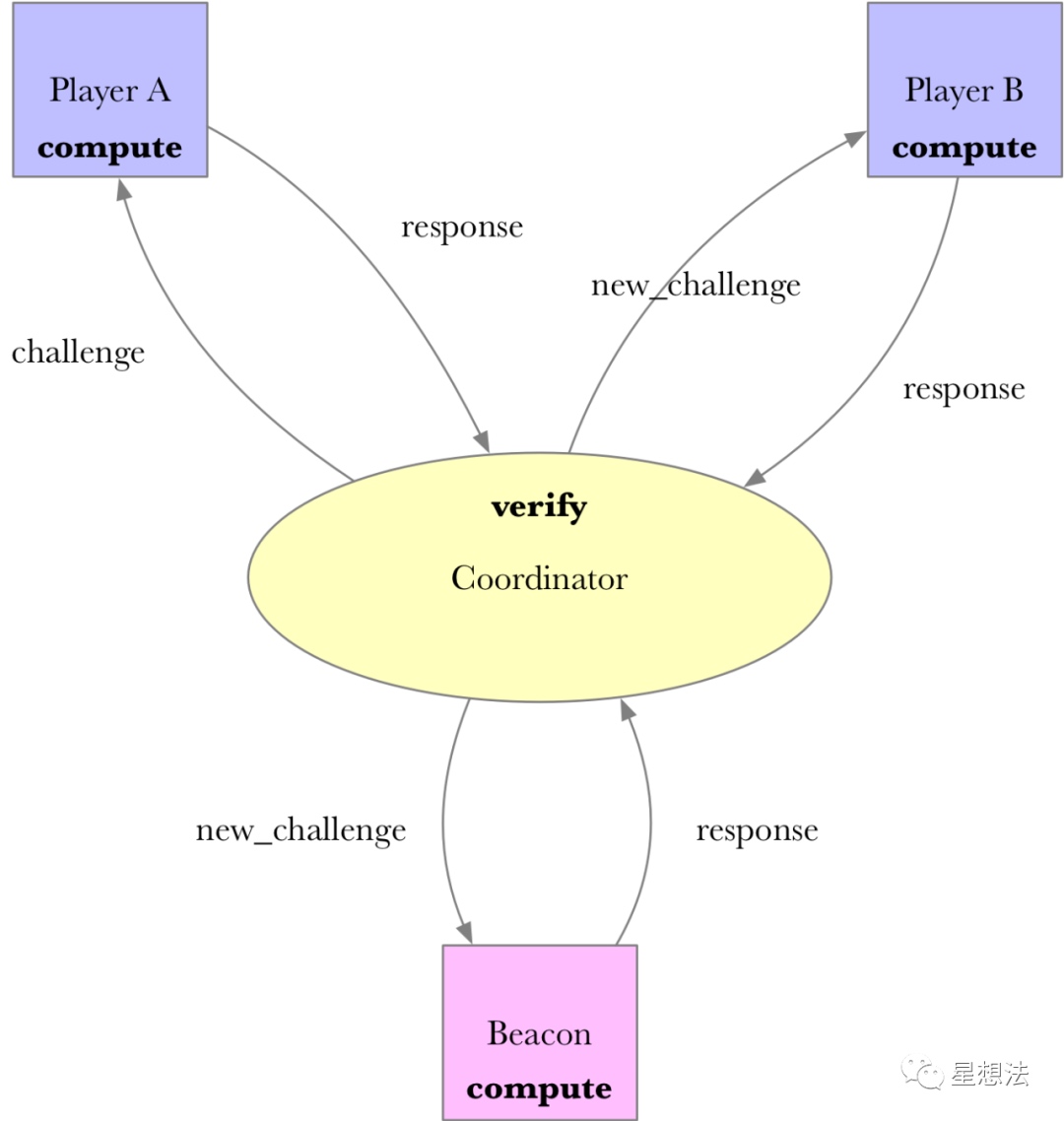
compute接受challenge文件,生成response文件。verify接受challenge文件,上一次的response文件,生成new_challenge。
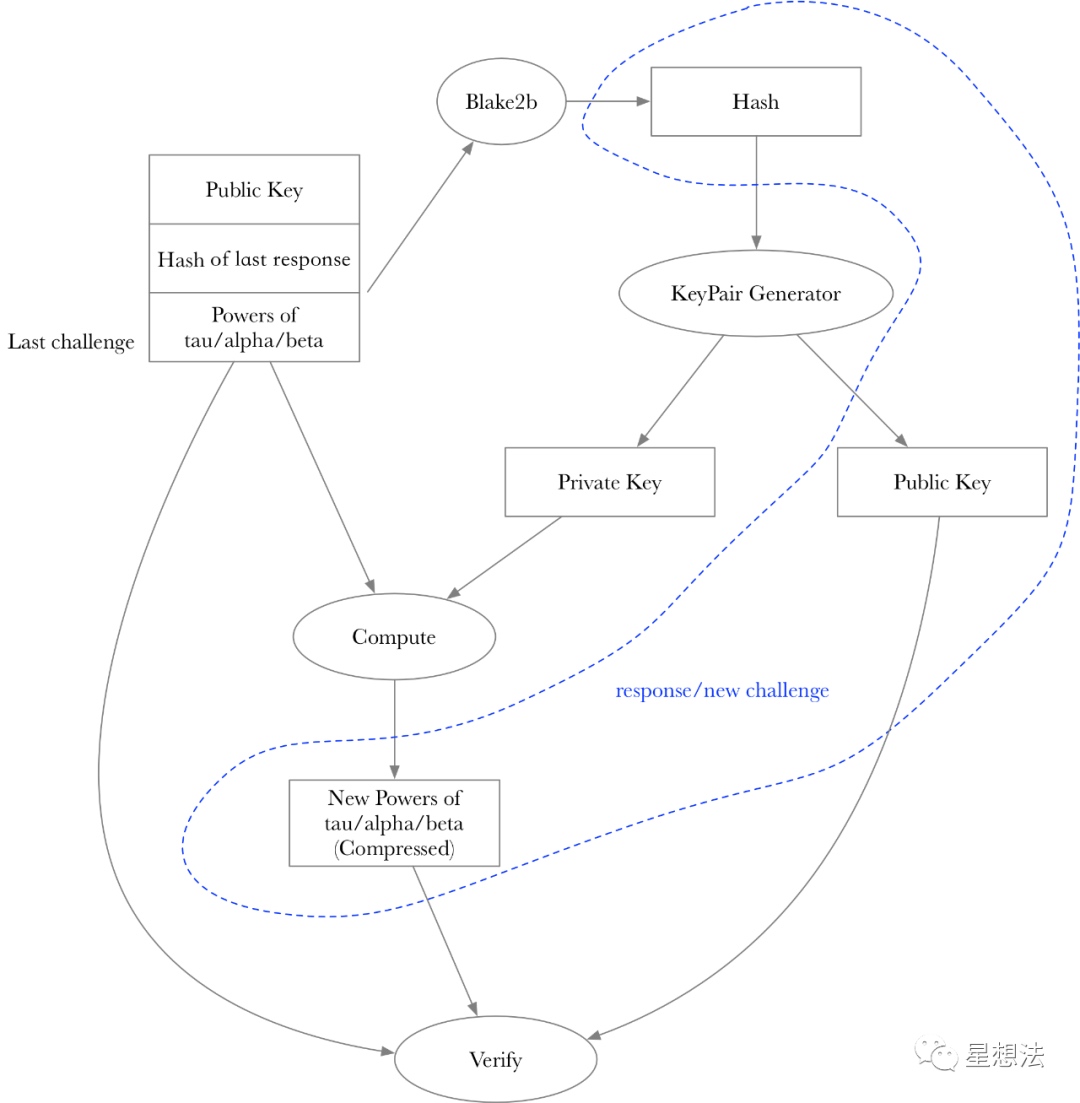
前一个challenge的hash值是作为下一个参与方生成密钥对的digest。某一个参与方生成的参数以及公钥信息会作为response,也是下一个参与方的challenge。因为上一个challenge的hash用于验证下一次的公钥的验证,从而确定了参与方的顺序。
整个协议的流程如下:
new -> compute -> (verify) compute ... -> (verify) compute -> (verify) beacon
总结:
powersoftau,采用MPC以及随机Beacon,完成可信设置。通过POK算法实现可验证的密钥对,并建立和上一个参与方计算结果的绑定。参与可信设置的人数可扩展,并且参与方只需要按照顺序一个个的进行指定的计算即可。协调方在接收到某个参与方的计算后,验证后,发送给下一个参与方。

- 转载
- 学分: 4
- 分类: 零知识证明
- 标签: powersoftau 零知识证明 MPC
- ZK编年史:哈希登场 67 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 300 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 252 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 332 浏览
- Zcash:比特币遗忘的隐私 406 浏览
- ZK编年史:计算模型 282 浏览
- lambdaworks 2026 年更新路线图和优先级 334 浏览
- 2026年构建机构级DeFi平台真正需要什么 824 浏览
- zkMesh:2026年1月回顾 423 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 603 浏览
- Zcash 的时代到来了 717 浏览
- ZK 编年史:电路(第二部分) 407 浏览

