格密码的HD钱包 - 密码学

摘要

本文档描述了一种与格密码学配合使用的分层确定性钱包方案。

动机

分层确定性钱包 HD-Wallets 已经成为区块链中事实上的标准。随着区块链行业讨论后量子未来，我们希望将这种技术应用于格密码学中的密钥，因为备份单个种子短语（可以预先生成无限个不相连的密钥）的用户体验，比用户每次执行操作都要备份同一个钱包要好得多。

我们专注于 Dilithium 签名方案，因为它是第一个最终确定的 NIST 后量子签名，并且很可能成为行业标准。

将格密码学适配到 HD 设置中的挑战是双重的。首先，HMAC-SHA512 的输出不能直接用作格私钥。对于 Falcon 和 Dilithium

我们需要形成格的“良好基”（小向量）的多项式，并且密钥生成算法使用拒绝采样，如果不进行修改，这不适合 HD 钱包方案。

第二个挑战是，在 BIP32 中，非硬化密钥是通过椭圆曲线点（公钥）的加法来推导的，而对于格来说，没有等效的操作：格公钥的集合在加法或乘法下不是闭合的。

我们在这个 QIP 中解决了第一个挑战，并且不尝试支持非硬化密钥。据我们所知，第二个挑战是否可以在格密码学设置中克服，仍然是一个开放的研究问题。非硬化密钥用于仅观看或审计钱包，对于 HD 钱包的主要用途而言并非必不可少，因此我们不认为这是一个关键的缺点。

规范

核心思想是在每次迭代时，使用 HMAC 输出的熵作为多项式采样的 RNG。在 BIP32 中，HMAC 输出的一半用作私钥，可以直接使用（在“硬化”情况下），也可以添加到先前的私钥中（在“非硬化”情况下）。这之所以有效，是因为椭圆曲线密码算法的结构，其中私钥可以被视为一个整数，该整数乘以椭圆曲线组中的生成点。

在 Falcon 和 Dilithium 中，密钥生成算法在密钥推导过程中消耗 <= 64 字节的熵。我们可以简单地将 HMAC 的整个输出馈送到密钥生成过程中，而不是像以前那样将一半用作私钥本身，但是为了最大程度地与 BIP44 钱包 互操作，我们仅使用输出的一半。这使得该方案与 BIP32 中的硬化密钥推导相同。

NIST 在此处 支持使用种子作为默认密钥格式的这种技术。

参考实现

格 HD 钱包的实现在此处。针对由 pq-crystals 生成的测试向量进行测试，pq-crystals 是 dilithium 的参考实现，由该标准的作者用 C 语言编写。

两个钱包版本都使用 rust 库 bip39 从助记词“种子短语”获取到“种子”。然后，我们通过 HMAC-SHA512 从种子派生出“主密钥”，该密钥构成了密钥树的根，每个边表示 HMAC-SHA512(R || 0x00 || L || child_index)，其中 L || R 是树中父节点的拆分值，如 BIP32 标准中所述。

基本原理

我们最初考虑使用 Falcon，因为它具有更小的密钥和签名。为此，我们依赖于 Thomas Pornin 的 rust-fn-dsa FALCON 签名算法实现，并进行了一些小的修改以允许外部生成的熵。Thomas Pornin 是 FALCON 标准的作者之一，也是该算法的 PQClean C 语言实现的作者。Falcon 钱包的实现在此处。

后来我们注意到（来自 Thomas Pornin），Falcon 标准没有完全指定密钥生成路径，因此我们已决定切换到 ml-dsa（以前是 dilithium）。 Dilithium 具有多个优点。它是

• 更简单
• 更快
• 具有确定性的密钥生成
• 已经由 NIST 最终确定

缺点是更大的密钥、更大的签名和更慢的验证。

在任何情况下，格密钥和签名都比椭圆曲线大得多，因此我们只需要为更多的磁盘空间付费。

Dilithium 和 Falcon 都需要 <= 64 字节的熵作为密钥生成过程的输入，因此我们可以简单地使用 HMAC-SHA512 的前 32 字节输出作为熵源。使用格密码学显然无法实现非硬化的用例，因此我们将其省略。

关于 HMAC-SHA512 的量子安全性，针对哈希函数的主要量子攻击是 Grover 算法，该算法在搜索未排序的数据库（在我们的例子中为哈希原像）时提供了二次加速。这会将安全位数减半，因此 512 → 256，256 → 128 等。

这适用于所有哈希函数，因此任何经典安全的哈希算法都会遇到相同的问题。另一方面，已经证明 Grover 算法是渐近最优的，因此我们不应期望另一种量子算法比 Grover 算法对安全哈希函数做得更好。

与哈希函数相比，区块链的数字签名更容易受到量子攻击，因为 Shor 算法 将从公钥找到椭圆曲线私钥的难度从指数级（Pollard 的 rho）降低到对数多项式 O(log^3(n))，其中 n 是 比特数。

因此，我们优先考虑保护数字签名免受量子

攻击，并保持哈希函数不变。

版权

本规范已发布到公共领域。

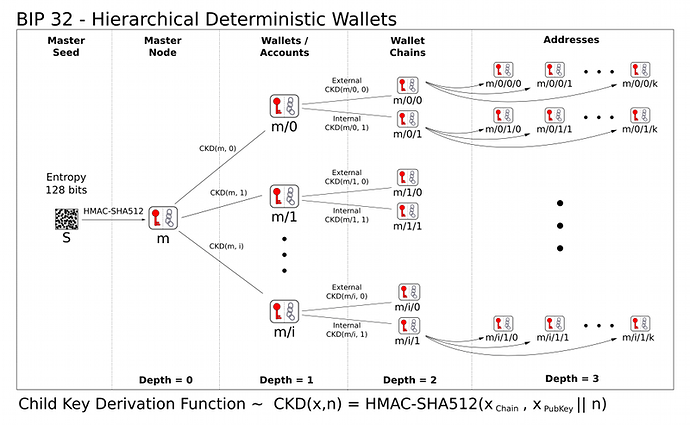
请参见此图，以获取 BIP32 的摘要。

\ QIP-0002-1800×493 101 KB

此提案最初作为 Quantus 改进提案发布此处

• 原文链接： ethresear.ch/t/hd-wallet...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～