格密码学基础(三):LWE和其他格问题的难度
- XPTY
- 发布于 2025-11-13 20:37
- 阅读 594
本文从几何角度介绍了LWE问题,解释了格的概念,包括整数格和q元整数格的定义和性质,以及商群、行列式和到格的距离。讨论了随机格中短向量的存在性,介绍了SIS问题,并探讨了如何使用求解SIS的算法来求解LWE问题,最后给出了实际参数的选取建议,以及LWE和SIS在密码学中的应用,例如 Kyber 和 Dilithium。
❝
原文:https://eprint.iacr.org/2024/1287
作者:Vadim Lyubashevsky
译者:Kurt Pan
我们现在将给出LWE问题的几何视角。虽然这种联系对于理解大多数密码构造如何工作并不是真正必要的,但它对于理解它们的安全性至关重要。
3.1 格
LWE问题的几何解释的核心是被称为格 的对象。一个$m$维整数格$\Lambda$简单地说是群$(\mathbb{Z}^m, +)$的一个子群。这样的群可以通过称为基的生成集来描述。特别地,由(满秩)基$\mathbf{B} \in \mathbb{Z}^{m \times m}$定义的格$\Lambda$是
$$ \Lambda = \mathcal{L}(\mathbf{B}) = {\mathbf{v} \in \mathbb{Z}^m : \exists \mathbf{z} \in \mathbb{Z}^m \text{ 使得 } \mathbf{Bz} = \mathbf{v}} $$
在本章中,我们将只限制自己研究称为$q$元整数格_ 的特殊类型的格,因为这些是在密码构造中使用的格。它们还具有很好的理论性质,即渐近地,在这些格的随机实例上求解某个问题与在 任何 格上求解某个问题一样困难。这是著名的最坏情况到平均情况归约研究路线[Ajt96, Reg09],它构成了基础并推动了基于格的密码学的发展。
对于矩阵$\mathbf{A} \in \mathbb{Z}_q^{n \times m}$,由$\mathbf{A}$定义的$q$元格$\Lambda$是
$$ \Lambda = \mathcal{L}_q^{\perp}(\mathbf{A}) = {\mathbf{v} \in \mathbb{Z}^m : \mathbf{Av} \equiv \mathbf{0} \pmod{q}} $$
不难看出,在通常的向量加法运算下,上述集合是一个群。对于熟悉线性码的读者来说,上述两个格的定义类似于使用生成矩阵或奇偶校验矩阵来描述一个码。更具体地说,我们将处理的格是
$$ \Lambda = \mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n]) $$
其中$\mathbf{I}_n$是$n \times n$单位矩阵。这不是太大的限制,因为如果$\mathbf{A}$包含$n$列在$\mathbb{Z}_q$上线性独立(不失一般性,假设$\mathbf{A} = [\mathbf{A}_1 \mid \mathbf{A}_2]$,其中$\mathbf{A}_2 \in \mathbb{Z}_q^{n \times n}$是可逆的),那么我们可以写$\mathbf{A}_2^{-1} \mathbf{A} = [\mathbf{A}_2^{-1} \mathbf{A}_1 \mid \mathbf{I}]$并且$\mathcal{L}_q^{\perp}(\mathbf{A}) = \mathcal{L}_q^{\perp}(\mathbf{A}_2^{-1} \mathbf{A})$,其中后者就是上式形式。对于上式形式的格,在"生成"矩阵表示和"奇偶校验"矩阵表示之间切换也很容易。容易验证
$$ \mathcal{L}_q^{\perp}\left(\left[\mathbf{A} \mid \mathbf{I}_n\right]\right)=\mathcal{L}\left(\left[\begin{array}{cc} -\mathbf{I}_m & \mathbf{0} \\ \mathbf{A} & q \mathbf{I}_n \end{array}\right]\right) $$
特别地,如果$\mathbf{Av}_1 + \mathbf{v}_2 \equiv \mathbf{0} \pmod{q}$,那么存在某个向量$\mathbf{r}$使得$\mathbf{Av}_1 + \mathbf{v}_2 = q\mathbf{r}$。则
$$ \left[\begin{array}{cc} -\mathbf{I}_m & \mathbf{0} \\ \mathbf{A} & q \mathbf{I}_n \end{array}\right] \cdot\left[\begin{array}{c} -\mathbf{v}_1 \\ \mathbf{r} \end{array}\right]=\left[\begin{array}{l} \mathbf{v}_1 \\ \mathbf{v}_2 \end{array}\right] . $$
上述表明$\mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$中的所有向量也在$\mathcal{L}\left(\left[\begin{array}{cc}-\mathbf{I}_m & \mathbf{0} \\ \mathbf{A} & q \mathbf{I}_n\end{array}\right]\right)$中,反之亦然。
3.1.1 商群和行列式
满秩格$\Lambda \subseteq \mathbb{Z}^m$的行列式,记为$\det(\Lambda)$,是$\Lambda$在空间$\mathbb{Z}^m$中密度的倒数。也就是说,如果我们定义集合$S_r = {\mathbf{z} \in \mathbb{Z}^m : |\mathbf{z}| < r}$,那么
$$ \det(\Lambda) = \lim_{r \rightarrow \infty} \frac{|S_r|}{|\Lambda \cap S_r|} $$
如果$\Lambda = \mathcal{L}(\mathbf{B})$对于满秩矩阵$\mathbf{B} \in \mathbb{Z}^{m \times m}$,那么$\det(\Lambda) = |\det(\mathbf{B})|$,其中右边是$\mathbf{B}$的通常的矩阵行列式。例如,$(n+m)$维格的行列式是$\det(\Lambda) = |\det(\mathbf{B})| = q^n$。满秩$m$维格$\Lambda$的行列式的另一个等价定义是商群$\mathbb{Z}^m / \Lambda$的大小。
格的奇偶校验表示,$\Lambda = \mathcal{L}_q^{\perp}(\mathbf{A})$,便于检查$\mathbb{Z}^m$中的两个向量是否在$\mathbb{Z}^m / \Lambda$的同一陪集中。特别地,$\mathbf{z}_1$和$\mathbf{z}_2$在同一陪集中当且仅当$\mathbf{Az}_1 \equiv \mathbf{Az}_2 \pmod{q}$。有了这个观察,很容易看出当$\Lambda = \mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$时,恰好有$q^n$个陪集;这与我们之前观察到的格的行列式是$q^n$一致。
3.1.2 到格的距离
对于$m$维格$\Lambda$和任何向量$\mathbf{r} \in \mathbb{Z}^m$(不一定在$\Lambda$中),从$\mathbf{r}$到格的$\ell_p$范数距离定义为
$$ \Deltap(\mathbf{r}, \Lambda) = \min{\mathbf{v} \in \Lambda} |\mathbf{v} - \mathbf{r}|_p $$
观察到对于属于$\mathbb{Z}^m / \Lambda$的同一陪集的任意两个元素$\mathbf{r}_1$和$\mathbf{r}_2$,$\Delta_p(\mathbf{r}_1, \Lambda) = \Delta_p(\mathbf{r}_2, \Lambda)$,因此距离对于陪集来说也是良定义的概念。因此,如果$\Lambda = \mathcal{L}_q^{\perp}(\mathbf{A})$并且$\mathbf{t} \equiv \mathbf{Az} \pmod{q}$定义了陪集$\mathbf{z} + \Lambda$,那么
$$ \Delta_p^C(\mathbf{t}, \Lambda) = \Delta_p(\mathbf{z}, \Lambda) $$
为清晰起见,写$\Delta^C$而不是$\Delta$来表示$\mathbf{t}$是陪集在$\mathbf{A}$下的像,而不是某个陪集代表。
我们现在将证明一些关于随机格中短向量的(不)存在性的命题。为简单起见,我们只在$q$是素数的情况下证明它们,但更仔细地,可以对所有$q$证明类似的命题。引理2和3表明随机陪集远离随机$q$元格,并且$q$元格没有非常短的向量。引理4证明了部分逆命题,给出了任何$q$元格中最短向量长度的下界。
❝
引理2. 对于任何素数$q$和任何$\mathbf{t} \in \mathbb{Z}_q^n \backslash {\mathbf{0}}$,
$$ \Pr_{\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}}[\exists \mathbf{z} \in [\beta]^{n+m} \text{ 使得 } [\mathbf{A} \mid \mathbf{I}_n] \mathbf{z} \equiv \mathbf{t} \pmod{q}] \leq (2\beta+1)^{n+m} / q^n $$
证明. 由于$\mathbf{t}$非零,$\mathbf{z}$的某个系数也必须非零。不失一般性,假设它是第一个。那么对于固定的$\mathbf{z}$,我们有
$$ \begin{aligned} &\Pr_{\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}}[[\mathbf{A} \mid \mathbf{I}n] \mathbf{z} \equiv \mathbf{t} \pmod{q}] = \Pr{\mathbf{a} \leftarrow \mathbb{Z}_q^n, \mathbf{A}' \leftarrow \mathbb{Z}_q^{n \times (m-1)}}[[\mathbf{a} | \mathbf{A}' | \mathbf{I}_n] \begin{bmatrix} z1 \ \mathbf{z}' \end{bmatrix} \equiv \mathbf{t} \pmod{q}] \\&= \Pr{\mathbf{a} \leftarrow \mathbb{Z}_q^n}[\mathbf{a} z_1 \equiv \mathbf{t} - [\mathbf{A}' \mid \mathbf{I}n] \mathbf{z}' \pmod{q}] = \Pr{\mathbf{a} \leftarrow \mathbb{Z}_q^n}[\mathbf{a} \equiv z_1^{-1}(\mathbf{t} - [\mathbf{A}' \mid \mathbf{I}_n] \mathbf{z}') \pmod{q}] = q^{-n} \end{aligned} $$
其中$z_1^{-1} \pmod{q}$存在是因为我们假设$\gcd(z_1, q) = 1$。由于$[\beta]^{n+m}$中有$(2\beta+1)^{n+m}$个可能的向量,引理中的命题由并集界得出。
❝
推论1.
$$ \Pr_{\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}, \mathbf{t} \leftarrow \mathbb{Z}q^n}[\Delta{\infty}^C(\mathbf{t}, \Lambda) \leq \beta] \leq (1 - |\mathbb{Z}_q^*| / q)^n + (2\beta+1)^{n+m} / q^n, $$
其中$\Lambda = \mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$。
格密码学中$q$的一些"流行"设置是素数$q$和$q$是2的幂。在这两种情况下,概率界中的第一项在$n$中都是可忽略的(分别为$(1/q)^n$和$2^{-n}$)。因此,每当$\beta^{1+m/n} \ll q$时,随机陪集将距离$\Lambda$超过距离$\beta$。
下一个引理指出,在选择$\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}$时,格$\mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$具有短非零向量的概率很小。我们只对素数$q$证明这个引理,因为对于其他选择会有些混乱。引理的证明与引理2几乎相同。
❝
引理3. 对于任何素数$q$,
$$ \Pr_{\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}}[\exists \mathbf{z} \in [\beta]^{n+m} \backslash {\mathbf{0}} \text{ 使得 } [\mathbf{A} \mid \mathbf{I}_n] \mathbf{z} \equiv \mathbf{0} \pmod{q}] \leq (2\beta+1)^{n+m} / q^n $$
下一个引理是上面那个的逆命题;它给出了现有非零向量长度的下界。
❝
引理4. 对于任何$q$和任何$\mathbf{A} \in \mathbb{Z}_q^{n \times m}$,
$$ \exists \mathbf{z} \in [q^{n/(n+m)}]^{n+m} \backslash {\mathbf{0}} \text{ 使得 } [\mathbf{A} \mid \mathbf{I}_n] \mathbf{z} \equiv \mathbf{0} \pmod{q} $$
证明. 证明使用鸽笼原理。$\mathbb{Z}^{n+m}$中系数在0和$q^{n/(n+m)}$之间的向量有超过$(q^{n/(n+m)})^{n+m} = q^n$个。由于$\mathbf{Az} \bmod q$的值只有$q^n$种可能性,必须存在两个不同的$\mathbf{z}_1, \mathbf{z}_2$,其系数在上述范围内,使得$\mathbf{Az}_1 \equiv \mathbf{Az}_2 \pmod{q}$。因此$\mathbf{z}_1 - \mathbf{z}_2 \in [q^{n/(n+m)}]^{n+m}$并且$\mathbf{A}(\mathbf{z}_1 - \mathbf{z}_2) \equiv \mathbf{0} \pmod{q}$。
根据引理3和4,我们看到在$\Lambda = \mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$中存在系数在$[\beta]$中的向量与以高概率不存在这样的向量之间的边界相当明确。引理4指出当$\beta = q^{n/(n+m)}$时,这样的向量总是存在。另一方面,如果我们设置$\beta < \frac{1}{4} q^{n/(n+m)}$,那么$\Lambda$中存在系数在$[\beta]$中的向量的概率小于$2^{-(n+m)}$。
3.2 在随机格中寻找短向量(SIS问题)
关于格可以提出的一个基本计算问题是在其中找到一个"短"(非零)向量。当专门针对我们上面处理的格时,问题简单地变成找到一个非零$\mathbf{z} \in [\beta]^{n+m}$使得$[\mathbf{A} \mid \mathbf{I}_n] \mathbf{z} \equiv \mathbf{0} \pmod{q}$。引理4指出当$\beta = q^{n/(n+m)}$时,这样的向量肯定存在,但证明没有给我们任何找到它的方法。到目前为止,所有已知的(量子)算法用于找到这样的向量(对于均匀随机的$\mathbf{A}$)都需要$2^{\Omega(m+n)}$时间(参见[AKS01, ADRS15, AS18])。
随着$\beta$增加,问题确实变得更容易。显然,如果$\beta = q/2$,那么通过将与$\mathbf{I}_n$相乘的$\mathbf{z}$的系数设置为目标系数,问题就被平凡地解决了。对于较小的$\beta$值,人们会运行一个算法,该算法找到格中比最小向量大某个因子的向量。所有现代高效(即多项式时间)算法用于找到这样的短向量都是著名的LLL算法[LLL82]的后代,该算法保证找到长度最多为格中最短向量长度$2^{O(n+m)}$倍的向量。然后引理4意味着对于随机$\mathbf{A}$,LLL算法将在$\mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$中找到向量$\mathbf{z} \in [2^{\Omega(n+m)} \cdot q^{n/(n+m)}]^{n+m}$。
虽然LLL算法保证找到的向量的长度比最短向量的长度大指数倍(在格的维度中),但在实践中,这个指数不太大。在运行足够高维度(至少100)的格实验之前,甚至不清楚LLL对随机格的真实近似因子是指数的还是线性的。事实证明,近似因子确实在维度上是指数的,但指数的底数相当小。
[GN08, MR09]中的实验表明,可以在形如上文所述的随机格$\Lambda$(维度为$m+n$)中找到长度约为
$$ \det(\Lambda)^{1/(n+m)} \cdot \delta^{n+m} = q^{n/(n+m)} \cdot \delta^{n+m} $$
的非平凡向量(即那些不是$q$的倍数的向量),其中$\delta$取决于算法需要多少时间。为特定的$\delta$值推导LLL类型算法运行时间的良好近似相当复杂(参见[ACD+18, ADH+19]),超出了本教程的范围。作为一个非常粗略的经验法则,$\delta = 1.01$被认为在可及范围内,而$\delta = 1.005$可能永远不会在足够高维度的格(例如超过500)上实现。
注意,如果格$\mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$的维度非常大,可以从$\mathbf{A}$中任意删除许多列并在得到的格上运行LLL。特别地,最优的格维度是
$$ \sqrt{n \log q / \log \delta} $$
(见[MR09, 第3章]),这导致找到的非平凡向量的$\ell_2$范数为
$$ 2^{2\sqrt{n \log q \log \delta}}. $$
❝
[MR09]仅声称当找到的向量的$\ell2$-范数小于$q$时此界是有效的,并且对于超过$q$时不做任何声明。然而,从渐近意义上看,当例如试图找到$\ell{\infty}$-范数有界且远小于$q/2$的短向量时,此界似乎仍然相当准确。那么仍然可以使用该向量对应的$\ell_2$-范数的此界。存在一些已知的小优化(例如见[DKL+18]),但作为粗略指南,此界仍然相当好。
在随机格中找到短向量的问题被称为SIS(短整数解)问题 。已知求解这个问题的随机实例至少与求解所有格中的某些相关问题一样困难[Ajt96, MR07]。我们将写$\text{SIS}_{n,m,q,\beta}$为当给定如前文所述随机格时找到系数在$[\beta]$中的向量的问题。
❝
定义4. 对于正整数$m, n, q$和$\beta < q$,$\text{SIS}_{n,m,q,\beta}$问题要求对于随机选择的矩阵$\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}$,找到向量$\mathbf{s}_1 \in [\beta]^m$和$\mathbf{s}_2 \in [\beta]^n$使得$\mathbf{As}_1 + \mathbf{s}_2 = \mathbf{0} \pmod{q}$。
注意,根据引理3,当$\beta \ll \frac{1}{2} q^{n/(n+m)}$时,$\text{SIS}{n,m,q,\beta}$问题是平凡困难的,而根据上文随着$\beta$增长问题变得更容易。还要注意到,一旦$m$大于$\sqrt{n \log q / \log \delta}$,它对问题的难度就没有影响,因为它不出现在找到的向量大小的公式中。这与$\text{LWE}{n,m,q,\beta}$问题的情况非常相似,其中参数$n$不太重要。正如在那种情况下,我们只写$\text{SIS}_{n,q,\beta}$。
在定义4中定义的$\text{SIS}_{n,m,q,\beta}$问题使用范数,而上文找到向量的难度是在$\ell2$范数中。在$\ell{\infty}$范数中定义问题的原因是因为在Dilithium签名方案中,该方案被设计为避免复杂的操作,困难问题自然地在$\ell{\infty}$范数中。可以得出关于$\ell{\infty}$范数中问题难度的某些结论的一种方法是注意到找到$\ell_{\infty}$范数为$\beta$的向量至少需要找到$\ell_2$范数乘以维度的平方根的格向量。
❝
Dilithium签名方案中的所有采样都是从均匀分布进行的。如果从计算上稍微复杂一些的分布进行采样,可以获得更高效的签名方案版本(例如[Lyu12, DFPS22])。
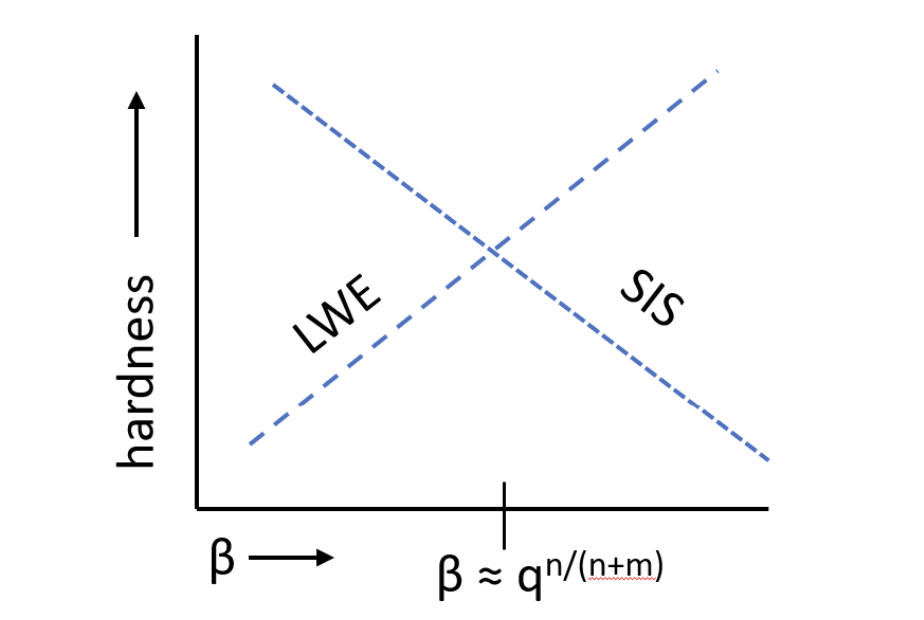
图2: 固定$n, m, q$和变化$\beta$时$\text{LWE}{n,m,q,\beta}$和$\text{SIS}{n,m,q,\beta}$的难度。这些线不是为了描述这些问题的具体难度,而是为了说明这些问题的难度对$\beta$的依赖性。交点大约在$\beta = q^{n/(n+m)}$处。
3.3 LWE格
现在让我们用格的语言重新表述第2.3节中的$\text{LWE}_{n,m,q,\beta}$问题。如果我们选择随机$\mathbf{A} \leftarrow \mathbb{Z}_q^{n \times m}$和随机$\mathbf{s} \leftarrow [\beta]^m, \mathbf{e} \leftarrow [\beta]^n$,并输出$(\mathbf{A}, \mathbf{t} = \mathbf{As} + \mathbf{e})$,那么这与输出格$\Lambda = \mathcal{L}_q^{\perp}([\mathbf{A} \mid \mathbf{I}_n])$(对于随机$\mathbf{A}$)和$\mathbb{Z}q^m / \Lambda$中的陪集$\mathbf{t}$使得$\Delta{\infty}^C(\mathbf{t}, \Lambda) \leq \beta$是相同的。另一方面,对于随机$\mathbf{u} \leftarrow \mathbb{Z}q^n$输出$(\mathbf{A}, \mathbf{u})$类似于输出格$\Lambda$和$\mathbb{Z}^m / \Lambda$的随机陪集。因此$\text{LWE}{n,m,q,\beta}$问题可以重新表述为试图区分接近格的陪集和随机陪集。
我们的加密方案有$m = n$且为了正确性需要$\beta^2 = O(q/\sqrt{m})$,因此$\beta \ll \sqrt{q}$。从推论1,这意味着随机陪集将比$\beta$更远离格。因此使加密方案工作的参数的$\text{LWE}_{n,m,q,\beta}$问题可以看作是区分接近格的陪集与远离格的陪集。
我们现在可以展示如何使用求解SIS的算法来求解LWE。如果我们得到一个$\text{LWE}_{n,m,q,\beta}$实例$(\mathbf{A}, \mathbf{t} = \mathbf{As} + \mathbf{e})$,那么将其与随机区分的想法是找到短向量$\mathbf{r}_1, \mathbf{r}_2$使得
$$ \mathbf{r}_1^T \cdot \mathbf{A} + \mathbf{r}_2^T = \mathbf{0}. $$
一旦我们找到这样的向量,我们计算$\mathbf{r}_1^T \cdot \mathbf{t}$。如果$\mathbf{t}$是均匀随机的,那么这将是$\mathbb{Z}_q$中的随机元素。另一方面,如果$\mathbf{t} = \mathbf{As} + \mathbf{e}$,那么
$$ \mathbf{r}_1^T \cdot \mathbf{t} = \mathbf{r}_1^T \cdot \mathbf{A} \cdot \mathbf{s} + \mathbf{r}_1^T \cdot \mathbf{e} = -\mathbf{r}_2^T \cdot \mathbf{s} + \mathbf{r}_1^T \cdot \mathbf{e} $$
由于$\mathbf{s}, \mathbf{e}$具有小范数,并且我们假设我们也找到了短的$\mathbf{r}_1, \mathbf{r}_2$,上述意味着$\mathbf{r}_1^T \cdot \mathbf{t}$也将具有小范数,这将允许我们将LWE实例与随机实例区分开来,从而求解LWE问题。
找到$\mathbf{r}_1, \mathbf{r}_2$等价于在格$\mathcal{L}_q^{\perp}([\mathbf{A}^T \mid \mathbf{I}_m])$中找到短向量。我们知道可以在这个格中找到范数为$2^{2\sqrt{m \log q \log \delta}}$的向量(注意因为我们使用了$\mathbf{A}^T$,$n$变成了$m$),这意味着$|(\mathbf{r}_1, \mathbf{r}_2)| \leq 2^{2\sqrt{m \log q \log \delta}}$。如果$\mathbf{s}, \mathbf{e}$的系数从$[\beta]$中均匀随机选择,那么每个坐标的方差是
$$ \frac{1}{2\beta+1} \sum{i=-\beta}^{\beta} i^2 = \frac{2}{2\beta+1} \sum{i=1}^{\beta} i^2 = \frac{2}{2\beta+1} \cdot \frac{\beta \cdot (\beta+1) \cdot (2\beta+1)}{6} = \frac{\beta \cdot (\beta+1)}{3}, $$
因此标准差是$\sqrt{\frac{\beta \cdot (\beta+1)}{3}}$。
如果假设每个系数不是均匀分布而是标准差为$\sqrt{\frac{\beta \cdot (\beta+1)}{3}}$的正态分布(这可以通过中心极限定理在渐近上证明,但对于格密码学中使用的参数来说它已经是一个非常好的近似),那么我们知道$-\mathbf{r}_2^T \cdot \mathbf{s} + \mathbf{r}_1^T \cdot \mathbf{e}$的分布是标准差为
$$ |(\mathbf{r}_1, \mathbf{r}_2)| \cdot \sqrt{\frac{\beta \cdot (\beta+1)}{3}} \approx 2^{2\sqrt{m \log q \log \delta}} \cdot \sqrt{\frac{\beta \cdot (\beta+1)}{3}} $$ 的正态分布。已知(见[MR07])如果我们有一个标准差大于$\sqrt{3} \cdot q$的正态分布随机变量并且我们将其模$q$,那么结果在统计上接近(在$\approx 2^{-80}$内)均匀分布。因此如果上式大于$\sqrt{3} \cdot q$,那么算法将不起作用。换句话说,每当
$$ \sqrt{\beta \cdot (\beta+1)} > 3 \cdot q \cdot 2^{-2\sqrt{m \log q \log \delta}} $$
时,$\text{LWE}_{n,m,q,\beta}$将是安全的(至少对抗这个攻击,它似乎与任何其他已知方法一样好)。
3.4 实际参数
我们在第2.3.1节中看到了基于LWE问题的加密方案的构造。在表1中,我们列出了一些类似于在具体实际实例化中使用的样本参数——特别是如第4.7节中将描述的Kyber(ML-KEM)方案。当在第5节中构建签名方案时,方案的安全性既取决于SIS问题的难度又取决于LWE。在表2中,我们给出了在该方案的实例化中使用的样本参数。
表1: 一些类似于Kyber加密(ML-KEM)方案中使用的参数的$\text{LWE}{m,q,\beta}$问题的$\delta$难度近似值_
| $m$ | $\beta$ | $q$ | $\delta$ |
|---|---|---|---|
| 512 | 2 | $2^{12}$ | 1.0043 |
| 768 | 2 | $2^{12}$ | 1.0029 |
| 1024 | 2 | $2^{12}$ | 1.0022 |
表2: 一些类似于Dilithium(ML-DSA)签名方案中使用的参数的$\text{LWE}{m,q,\beta}$和$\text{SIS}{n,q,\beta}$问题的$\delta$难度近似值
$\text{LWE}_{m,q,\beta}$参数:
| $m$ | $\beta$ | $q$ | $\delta$ |
|---|---|---|---|
| 1024 | 2 | $2^{23}$ | 1.004 |
| 1280 | 4 | $2^{23}$ | 1.003 |
| 1792 | 2 | $2^{23}$ | 1.0023 |
$\text{SIS}_{n,q,\beta}$参数:
| $n$ | $\beta$ | $q$ | $\delta$ |
|---|---|---|---|
| 1024 | $2^{18}$ | $2^{23}$ | 1.0041 |
| 1536 | $2^{20}$ | $2^{23}$ | 1.0032 |
| 2048 | $2^{20}$ | $2^{23}$ | 1.0025 |
值得指出的是,这些表中的参数是基于当前已知的最佳格归约算法设置的(参见得到良好支持的在线格估计器项目[APS15])。例如,图2中LWE的难度图,我们看到随着噪声$\beta$增加,问题的难度单调增加,没有任何突然跳跃。特别地,如果$q/\beta = 2^{m/k}$,其中$m$是格的维度并且$1 \leq k \leq m$,那么最佳已知算法在(忽略多项式因子)大约$2^k$时间内求解LWE问题。
但是对于所有"小"值$\beta$,问题是容易的且在某个点有突然跳跃并非不可能。这实际上正是对应于某个代数环的理想的格中找到短向量的问题所发生的情况[CGS14, BS16, CDPR16, CDW17]。当$q/\beta > 2^{\sqrt{m}}$时(即当上一段中的$k$小于$\sqrt{m}$时),问题可以在量子多项式时间内求解(而不是$2^k$),但一旦比率$q/\beta$变小——即$k > \sqrt{m}$,问题的难度就跳回到$2^k$。因此,某些尚未发明的(量子)算法可能在特定范围的比率$q/\beta$上表现好得多,但在其他地方没有改进,这并非不可能。因此,出于安全目的,基于$\text{LWE}_{n,m,q,\beta}$问题的难度构建密码学时,让$q/\beta$尽可能小可能是谨慎的。
❝
如您喜歡,請打賞支持我!👇
讓我們一起向 付費圍牆花園 和 廣告推薦注意力經濟 宣戰,讓賽博空間重新清朗!
- 本文转载自: mp.weixin.qq.com/s/lYZXi... , 如有侵权请联系管理员删除。
- 2026年:PQC签名迁移的启动 172 浏览
- 666 - PQC 野兽的密文大小? 359 浏览
- 666 - 后量子密码巨兽的密文大小? 619 浏览
- 格密码学基础(五)(完结篇):基于Σ-协议构造数字签名 411 浏览
- 格密码学基础(四):多项式环上的加密 548 浏览
- 玩转LaBRADOR:用递归构建紧凑的基于格的证明 517 浏览
- 格密码学基础(二):加密 356 浏览
- 格密码学基础(一):前言 495 浏览
- 【论文速递】DilithiumRK:基于Dilithium签名的后量子比特币区块链 392 浏览
- 格密码的HD钱包 - 密码学 1059 浏览
- 区块链的后量子迁移 1244 浏览


