Circom 常见陷阱及规避方法 — 第二部分

在第一部分中，我们讨论了滥用 hint 和 assertion 如何导致电路约束不足。我们还看到了在使用 circomlib 的 Num2Bits 和 Bits2Num 时，别名错误如何带来麻烦。在这篇文章中，我们将深入探讨编写 Circom 时需要注意的另外三个陷阱。事不宜迟，让我们直接开始吧！

输出约束很容易被忘记

在 Circom 中，许多模板都假定它们的调用者会显式地约束它们的输出。如果一个组件被使用时，其输出没有任何约束，这通常是一个危险信号，并可能导致严重的安全漏洞！

例如，考虑 circomlib 的 IsEqual() 模板：

template IsEqual() {
    signal input in[2];
    signal output out;

    component isz = IsZero();

    in[1] - in[0] ==> isz.in;

    isz.out ==> out;
}

下面的代码实例化了这个模板，并且似乎强制执行 x == y。但实际上，x 和 y 仍然可以取任何值。

pragma circom 2.1.6;

include "circomlib/comparators.circom";

template AssertEquality() {
    signal input x;
    signal input y;

    component eq = IsEqual();
    eq.in[0] <== x;
    eq.in[1] <== y;

    // BUG: eq.out 没有被约束为 1!
}

component main = AssertEquality();

// 这个 witness 将满足电路，
// 尽管 x 不等于 y。
/* INPUT = {
    "x": "42",
    "y": "24"
} */

记住，当且仅当 x 和 y 相等时，IsEqual() 才会输出 1。但是，在上面的例子中，它的输出并没有被约束为 1！因此，输出可以取任何值，也就是说，两个输入实际上从未被强制相等。你可以在 zkREPL 中测试这一点：上面的代码运行没有错误，即使 x 和 y 的 witness 值明显不相等。

修复方法很简单：在 AssertEquality() 模板的末尾添加 eq.out === 1;。有了这个约束，每当 x 和 y 不同时，电路就会正确地抛出一个错误。特别是，witness x = 42，y = 24 将不再满足电路。

作为第二个例子，下面的代码似乎强制 x 和 y 都等于 1，但由于与之前相同的原因，它并没有做到这一点。

include "circomlib/gates.circom";

template AssertAndIsTrue() {
    signal input x;
    signal input y;

    component and = AND();
    and.a <== x;
    and.b <== y;

    // BUG: and.out 没有被约束为 1!
}

注意：即使输出被约束为 1，上面的模板仍然是不安全的。你能发现错误吗？如果不能，别担心！我们将在下一节中介绍它。

对于一个更实际的例子，考虑 Circom-Pairing 库。它依靠大整数电路来表示大于有限域大小的值。为了强制某些信号保持在预期范围内，该库使用了一个 BigLessThan 模板：

template BigLessThan(n, k){
    signal input a[k];
    signal input b[k];
    signal output out;
    ...
}

a[k] 和 b[k] 是信号的输入数组，它们分别代表两个大整数 a 和 b 的 limb。BigLessThan 组件将这些 limb 作为输入，如果 a < b，则输出 1，否则输出 0。

注意：如果你不熟悉大整数，自己编写一个简单的 BigInt 库 是一个很好的入门方式。如果“limb”这个术语听起来很奇怪，这里 有一篇关于这个术语来源的简短阅读。

Circom-Pairing 库在其 CoreVerifyPubkeyG1 模板中使用了几个 BigLessThan 组件，以验证所提供的公钥的每个 limb 是否都在范围内：

template CoreVerifyPubkeyG1(n, k){
  ...
  var q[50] = get_BLS12_381_prime(n, k);

  component lt[10];

  for(var i=0; i<10; i++){
    lt[i] = BigLessThan(n, k);
    for(var idx=0; idx<k; idx++)
      lt[i].b[idx] <== q[idx];
  }

  for(var idx=0; idx<k; idx++){
    lt[0].a[idx] <== pubkey[0][idx];
    lt[1].a[idx] <== pubkey[1][idx];
    ...
    lt[9].a[idx] <== pubkey[9][idx];
  }
  ...

目的是约束 pubkey < q，以确保公钥被正确格式化为大整数。然而，输出 lt[i].out 从未被约束！就像我们之前的玩具示例一样，这意味着 电路实际上并没有强制执行 pubkey < q。恶意证明者可以提供一个超出范围的公钥，仍然可以生成有效的证明，因为没有任何东西检查 lt[i].out 是否等于 1。

再一次，修复方法很简单：确保每个 lt[i].out 都等于 1。一种有效的方法是在第二个 for 循环之后添加一个约束，要求所有十个输出的总和等于 10：

...

for(var idx=0; idx<k; idx++){
  lt[0].a[idx] <== pubkey[0][idx];
  lt[1].a[idx] <== pubkey[1][idx];
  ...
  lt[9].a[idx] <== pubkey[9][idx];
}

// Contrain each lt[i].out to equal 1.
for(var i=0; i<10; i++){
    r += lt[i].out;
}
r === 10;

...

有关该问题的更详细解释，我建议阅读这篇博客文章。

最后，我想强调的是，并非每个未使用的输出都会自动成为 bug。 例如，circomlib 的 Num2Bits(n) 通常用于有效地将给定的信号的范围限制在 [0,2n) 内。当用于该目的时，完全可以不约束其输出。有关此类用法的示例，请参见此处。(如果你对 Circom 仍然比较陌生，这可能没有意义。没关系！我们将在本系列的后续文章中让你快速了解范围检查。)\ \ 总结：组件输出不会自动受到约束。你必须显式添加约束。没有约束，输出可以取任意值。这个陷阱通常出现在比较器和布尔门中，尽管它并不局限于它们。有一些模板，例如 circomlib 的 Num2Bits，在某些用例中，未约束的输出可能是安全的。但在大多数情况下，未约束的输出应该敲响你的警钟。\ \

输入约束也很容易被忘记\

\ 正如未约束的输出是严重错误的常见来源一样，未约束的组件输入同样可疑，因为许多模板都假定你将在调用点自行处理输入约束。\ \ 作为一个简单的例子，让我们再次考虑 circomlib 的 AND 门：\ \

template AND() {
    signal input a;
    signal input b;
    signal output out;

    out <== a*b;
}

\ 这个门的标准用例是表明两个布尔标志是否为真。例如，它可以天真地使用如下：\ \

include "circomlib/gates.circom";

template RequireBothTrue() {
    signal input flagA;
    signal input flagB;

    component andGate = AND();
    andGate.a <== flagA;
    andGate.b <== flagB;

    // 我们的目的是要强制执行：
    // “两个标志都必须是 1”
    andGate.out === 1;
}

\ 这个模板对于布尔值来说表现正确，但这里有一个问题：circomlib 的 AND 门没有强制执行它自己的输入假设，也就是说，它从未检查它的输入是否真的是布尔值。它只是假设它们是。换句话说，我们可以欺骗我们的 AND 门，让它在完全垃圾的输入上输出“true”：\ \

pragma circom 2.1.6;

include "circomlib/gates.circom";

template RequireBothTrue() {
    signal input flagA;
    signal input flagB;

    component andGate = AND();
    andGate.a <== flagA;
    andGate.b <== flagB;

    // 我们的目的是要强制执行：
    // “两个标志都必须是 1”
    andGate.out === 1;
}

component main = RequireBothTrue();

// 我们可以欺骗我们的 AND 门，让它输出“true”，尽管我们
// 使用了完全没有意义的输入。

// 注意：回想一下，circomlib 的 AND 门只是它的
// 两个输入的乘积。为了确保 flagA * flagB = 1 (因此 andGate.out = 1)，
// 我们将 flagB 设置为 flagA 的模逆。

/* INPUT = {
    "flagA": "42",
    "flagB": "15113310554365213843932042062201451846854823038382499903982093366921391580307"
} */

\ 显然，这不是我们写“两个标志都必须是 1”时的语义。然而，修复方法很简单：我们必须在使用输入之前对其进行约束！\ \

include "circomlib/gates.circom";

template RequireBothTrueFixed() {
    signal input flagA;
    signal input flagB;

    // 在将两个标志用作 AND 门的输入之前，
    // 强制它们都是布尔值。
    flagA * (flagA - 1) === 0;
    flagB * (flagB - 1) === 0;

    component andGate = AND();
    andGate.a <== flagA;
    andGate.b <== flagB;

    // 现在这 *真的* 意味着“两个标志都必须是 1”。
    andGate.out === 1;
}

\ 总结：模板通常假设它们的输入已经满足某些属性，但不会通过约束来强制执行这些输入假设。如果你忘记在调用点强制执行这些前提条件，攻击者可以用无意义的输入来满足下游约束。\ \

比较操作作用于有符号整数\

\ 很容易假设，因为 Circom 在有限域上工作，所以信号和变量总是被视为 [0,p) 中的无符号整数。然而，这个假设是错误的！\ \ 作为一个反例，让我们考虑 Circom 对比较运算符 <、>、<= 和 >= 的定义。仔细观察后，你会意识到这些运算符依赖于一个内部函数，val:[0,p)→(−p2,p2], 定义如下：\ \ val(z)={z−p, if p/2+1≤z<pz, otherwise\ \ 换句话说，在比较两个数字之前，Circom 会将它们从 [0,p) 映射到 (−p2,p2]，如下图所示。\ \ 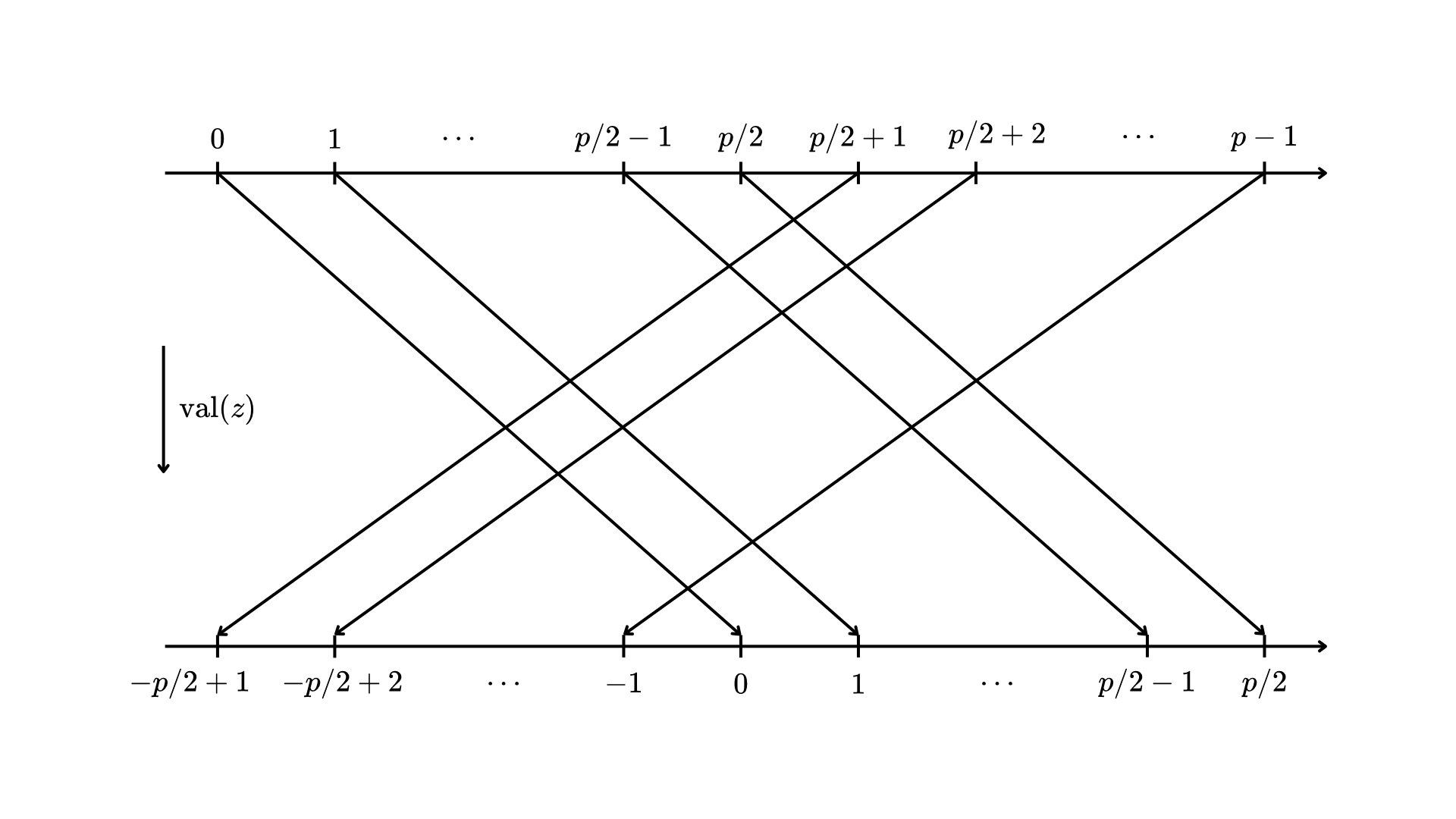\ \ 更正式地说，Circom 通过以下方式定义关系运算符:\ \ x◻yiffval(x mod p)◻val(y mod p)\ \ 其中 ◻ 表示 <, ≤, >, 或 ≥, 并且其中 “mod p” 解释了这样一个事实：在应用 val 之前，Circom 会首先将数字映射到区间[0,p)。\ \ 如果你不小心，这种行为可能会在 witness 生成期间导致令人惊讶的结果，如下面的示例所示：\ \

pragma circom 2.1.6;

template SurprisingWitGen() {
    signal input x;
    signal input y;
    signal isGreater;

    // 我们的目的是：如果 x > y，则 isGreater = 1，否则为 0。
    isGreater <-- x > y;

    log(isGreater);
}

component main = SurprisingWitGen();

// 注意：在这个特殊的例子中，我们展示了 p/2 > p/2 + 1。
// 使用 Circom 的默认素数，我们有：
// p/2 = 10944121435919637611123202872628637544274182200208017171849102093287904247808

/* INPUT = {
    "x": "10944121435919637611123202872628637544274182200208017171849102093287904247808",
    "y": "10944121435919637611123202872628637544274182200208017171849102093287904247809"
} */

\ 这表明 p/2>p/2+1 在 Circom 中确实是一个真命题。为了让你自己相信，我鼓励你在 zkREPL 中运行上面的代码。

现在你可能想知道：“Circom 到底为什么要故意应用如此令人困惑的重新映射，然后再比较两个值呢？！”\ \ 好问题！让我们考虑一下否则会发生什么：如果不应用 val，有限域元素在比较之前只会映射到 [0,p)。特别是，这意味着 −1 的表示将是 p−1，因此 Circom 会将语句 0<−1(≡p−1) 视为真。\ \ 因此，Circom 的理由如下：“我们无论如何都无法避免在我们的比较中出现一个奇怪的回绕点，因为有限域本质上是循环的。然而，我们宁愿将这个不连续点“远远地”放置在一个巨大的数字上，例如 p/2+1，而不是直接放置在最常用范围的中间，也就是零附近的范围。这样一来，‘正常’范围内的比较行为直观，并且奇怪的边缘情况只会出现在非常大的数字上。”\ \ 但请注意，这种选择纯粹是定义的问题。有限域没有 "本身就有意义的" 元素的规范排序，因此对于这种选择没有 "错误" 或 "正确" 的选择。有些人可能更喜欢 Circom 的有符号算术，而另一些人可能觉得无符号算术更自然。只是 Circom 的开发者决定选择前者。因此，无论我们是否喜欢，我们都必须使用它。\ \ 总结：Circom 的 <、>、<= 和 >= 操作作用于有符号域代表。如果你的 witness 生成逻辑假设无符号语义，请确保考虑到 p/2+1 处的“截止”。\ \ 作为最后的评论，回想一下 Circom 的内置比较永远不是实际电路逻辑的一部分！像 <、>，甚至 == 这样的运算符不会像在传统编程语言中那样在运行时“运行”。Circom 电路只是一组方程（仅由域元素上的加法和乘法组成），当生成和验证证明时，这些方程必须成立。因此，比较运算符仅在 witness 生成期间使用，而不是在电路本身中使用。\ \ 也就是说，可以直接在电路级别实现比较逻辑！这正是 circomlib 的比较器模板（例如 LessThan）的目的。\ \ 我们将在本系列的后续文章中仔细研究它们及其常见的陷阱。敬请关注！\ \ 特别感谢 Giorgio Dell'Immagine, 0xAlexSR, 0xStrapontin, 0xteddav, 和 Georgios Raikos 花费宝贵时间帮助我润色这篇文章。\ \ zkSecurity** 为包括零知识证明、MPC、FHE 和共识协议在内的密码系统提供审计、研究和开发服务。\ \ \ 了解更多 →

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～