ZK 编年史：多线性扩展

为了获得更具互动性的体验，请在我的个人博客 Arkana 上阅读此文章。

在上一期中，我们看到了第一个利用通用计算模型的协议实例：电路。

虽然概念上很有趣，但我们注意到，理想情况下，我们希望证明表示为电路的计算是正确执行的，而不是我们知道有多少输入满足电路 (回想一下我们研究了#SAT)。

但问题是，我们是否可以用我们现有的知识做到这一点。 嗯... 我们不能!

感觉我们 非常接近 了，而且说实话，我们也确实很接近了。 然而，要实现这一点，我们需要使用一个我们至今尚未谈及的小数学工具。

即使今天的内容在数学方面可能有点沉重，也不要忘记我们的最终目标：证明我们对某个电路有一个令人满意的输入！

因此，现在是我们结识一位新朋友的时候了：一个在我们即将到来的努力中非常有用的工具。

让我们开始行动吧！

建立直觉

在 sum-check 文章 中，我提到 0 和 1 是两个特殊的输入，因为在这两个点上计算多项式非常容易。

但说实话：在大多数现实场景中，我们实际上并不关心在 0 和 1 处的计算结果。 它们只是像其他数字一样——它们没有任何内在的语义含义。

这对于布尔电路可满足性来说并非如此，因为输入首先是真正的布尔变量！

因此，当 sum-check 要求我们验证布尔超立方体上的和时，一个显而易见的问题出现了：谁在乎呢？

我们什么时候才需要对这些特定点上的多项式求和？

答案可能会让你惊讶：一直，一直需要。 但要理解这一切，我们需要以 不同的视角 来看待这些布尔超立方体。

编码信息

这个问题的关键是将它们视为一种 编码信息 的方式。

让我们看一个具体的例子：一个简单的 数字列表。 假设我们有一个包含四个值的小列表，比如 [2, 3, 5, 8]。 要访问该列表的特定值，通常需要提供一个 索引。 因此，例如，要检索值 5，你需要请求列表中索引为 2 的值。

当然，假设我们使用的是 零索引！

现在，这是一个观察：索引只是 整数，并且这些整数都有 二进制表示。 更重要的是，这个小列表有 4 个可能的索引，在二进制中看起来像这样：

• 索引 0 → 00
• 索引 1 → 01
• 索引 2 → 10
• 索引 3 → 11

你明白我的意思了吧？ 每个索引只是 布尔超立方体 {0,1}² 中的一个点！

相同的信息，不同的表示！

有了这个，我们可以将读取列表中给定索引处的信息的动作想象成一个 函数，在这里我们可以假定索引是 超立方体 中的值 (在本例中只是一个布尔 正方形):

$f: \{0,1\}^² \rightarrow \mathbb{F}$

这只是数学符号，意思是“一个函数 f，它接受两个布尔变量，并返回域中的某个值”。

因此，按照例子，我们有：

• f(0,0) = 2
• f(0,1) = 3
• f(1,0) = 5
• f(1,1) = 8

好吧，好吧。 但这不只是更无意义的重新标记吗？

实际上，不是！ 你看，真正的关键在于我们如此不引人注目地引入的那个小函数 f。 隐含地，我们说这个函数能够 编码数据。

事实上，我们已经看到了一种获得上述函数的方法：插值。 显然，我们从该过程中获得的是一个 多项式。 正是通过这种类型的编码，sum-check 协议将变得相关。

酷！ 慢慢地，但肯定地，我们似乎正在取得进展。

但我希望你注意到一件事：回到我们对 拉格朗日插值 的介绍中，我们实际上侧重于 单变量 情况。 插值被呈现为一种从计算结果中获得单变量多项式的方法，我们将计算结果视为 (x, y) 对。

但是在 sum-check 协议中，我们使用了一个具有 v 个变量的多项式 g，而不是单个变量。 因此，在这里，我们所描述的插值将无法使我们得到所需类型的多项式。

因此，我们需要一些不同的东西。

多线性扩展

我们需要的是一种从定义在布尔超正方体上的 多元函数 (如上面的 f) 到 多元多项式 的方法。 为了方便起见，我们将调用该多项式 g，考虑到我们与 sum-check 的平行关系。

我们将以一种 非常特殊的方式 来做到这一点。 因为这里有两个重要的考虑因素：

• 在超正方体上的一致性：我们想要 编码 一些数据，这意味着 g 必须与布尔超正方体上的一组值匹配。
• 超出超正方体的扩展：在 sum-check 协议中，我们需要在 非 布尔字符串的点上计算 g。

结合起来，这两个条件精确地定义了 g 的行为：

它需要是一个多元多项式，其中每个输入都可以是一个有限域元素，并且其输出与布尔超立方体上的编码值匹配

是的…… 真是拗口。 让我们拆开它。

首先，我们要说的是，我们需要一个定义在这些集合上的函数：

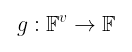
$g: \mathbb{F}^v \rightarrow \mathbb{F}$

也就是说，它取 𝔽 域中的 v 个输入，并且允许我们总共编码 2ᵛ 个值。 对于这些值，我们对函数有一系列的 限制：

• g(0, 0, …, 0, 0) 编码 f(0, 0, …, 0, 0) = k₀, 所以 g(0, 0, …, 0, 0) = k₀, 其中 k₀ 是 𝔽 中的某个元素。
• 然后，g(0, 0, …, 0, 1) 编码 f(0, 0, …, 0, 1) = k₁, 所以 g(0, 0, …, 0, 1) = k₁。
• 同样，g(0, 0, …, 1, 0) = k₂。
• g(0, 0, …, 1, 1) = k₃

以此类推。 因此，我们要求：

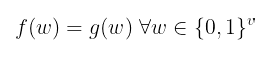
$f(w) = g(w) \ \forall w \in \{0,1\}^v$

这只是数学符号，意思是：g = f 仅在超立方体上成立。

这就是我们想要的构造。 就像我们 扩展 原始函数 f，以便输入可以取 0 和 1 之外的值，允许在更大的有限域上取值。 因此得名：多线性扩展 (multilinear extensions)。

但是等等，为什么是 多线性 (multilinear)？ 这到底是什么意思？

多线性性 (Multilinearity)

在发生任何混淆之前：多元 (multivariate) 和 多线性 (multilinear) 不是一回事。

正如我们已经知道的那样，多项式可以具有不同的次数，因为表达式本身中的不同项可以被提升到不同的整数幂。 我们甚至可以在这里稍微扩展一下语言，谈论 每个变量 的次数，因为给定变量在整个过程中被提升到的最大幂。

说一个多项式是多线性的实际上对表达式的外观施加了一个 强烈的限制：我们要说的是每个变量的次数 最多为 1。 为了完全清楚起见，这是一个多线性多项式：

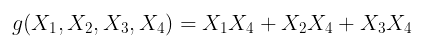
$g(X_1, X_2, X_3, X_4) = X_1X_4 + X_2X_4 + X_3X_4$

而这 不是：

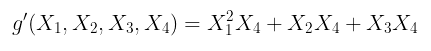
$g’(X_1, X_2, X_3, X_4) = X_1²X_4 + X_2X_4 + X_3X_4$

具有 X₁² 的那个单项使整个多项式非线性！

好吧…… 但是，再说一次，这有什么关系呢？

事实证明，施加这个条件有一些 好的结果。 你看，原则上，我们可以使用 任何次数 的多项式来扩展我们的原始函数 f。 事实上，有 无数种方法 可以做到这一点！

以我们的 4 元素列表 [2, 3, 5, 8] 为例。 我们可以构建如下多项式：

• g₁(X₁, X₂) = 2 + X₁ + 3X₂ + X₁X₂
• g₂(X₁, X₂) = 2 + X₁³ + 3X₂ + X₁X₂⁵
• g₃(X₁, X₂) = 2 + 100X₁⁷ + 3X₂ - 99X₁⁷ + X₁X₂

这三个多项式都正确地在 {0,1}² 上编码了列表，当然在其他任何地方都不同。 那么…… 具体来说，是什么让多线性性变得特别？

首先，多线性表达式 简单 且 高效。 这些多项式在某个时候需要进行 求值，在这方面，次数很重要。 与高次数表达式相比，多线性多项式的求值往往 成本较低，而且它们通常具有较少的系数，这也会影响通信成本。

此外，一些 可靠性论证 依赖于某些多项式具有较低的次数！

但这还不是全部。 当我们将自己限制在 多线性多项式 中时，恰好只有 一种方法 可以定义 g，使其满足我们所有的要求。 换句话说，在布尔超立方体上定义的某个函数 f 的 多线性扩展 (简称 MLE) 是 唯一 的。

见鬼，让我用更强烈的措辞来说明：

有一种自然的、唯一的方式来扩展在布尔超立方体上定义的函数 f 到一个多线性多项式

这非常强大。 非常强大，以至于我认为我们应该 证明 这个陈述。

可以随意跳过下一节。 我只是认为它值得一看，因为它是多线性扩展如此有用的属性！

唯一性

为了证明这一点，我们首先需要一个构建这样一个函数 g 的策略。

我们将这样做：对于 {0,1}ᵛ 中的每个点 w，我们将构建一个多项式，该多项式在 w 上计算为 1，在超立方体上的其他任何地方都计算为 0。

这 一定 听起来很熟悉。 你还记得我们在哪里看到过类似的东西吗？

是的，这正是我们定义 拉格朗日基 的方式！ 这几乎就是我们在这里所做的事情。

好的，那么，让我们定义它：

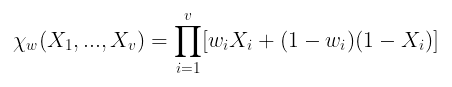
$\chi_w(X_1, …, Xv) = \prod{i=1}^{v} [w_iX_i + (1-w_i)(1-X_i)]$

这看起来可能有点奇怪，但是它的确可以正常工作：

• 当 X 值是 w 的坐标时，每一项都求值为 wᵢ² + (1 - wᵢ)²。 请注意，当 wᵢ 为 0 或 1 时，这等于 1。 因此，整个乘积的结果为 1。
• 当 X 取与 w 不同的某个其他值时，则至少有一个 Xᵢ 与 wᵢ 不同，因此 Xᵢ = 0 且 wᵢ = 1，反之亦然。 在这两种情况下，wᵢXᵢ + (1 - wᵢ)(1 - Xᵢ) 等于 0，因此将整个乘积折叠为 0。

要获得扩展，我们只需要将所有这些项加在一起，并乘以给定索引处的编码值 f(w)：

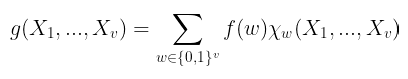
$g(X_1, …, Xv) = \sum{w \in \{0,1\}^v} f(w) \chi_w(X_1,…,X_v)$

你可以自己检查一下，此表达式是多线性的。 因此，我们构造了一个 有效的 f 的 MLE！

剩下的就是证明此表达式是 f 的唯一可能的 MLE。

我现在将开始稍微滥用符号，以使内容更加简洁。 当我说 p(X) 时，只需假设 X 是一个向量。 毕竟，这在我们正在使用的上下文中是有意义的！

为此，我们将做一些非常聪明的事情。 假设 p(X) 和 q(X) 是 f 的两个有效的 MLE。 从它们中，让我们构建这个多项式 h，它也是多线性的：

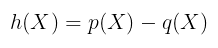
$h(X) = p(X) — q(X)$

因为 p(X) 和 q(X) 是有效的 MLE，所以它们在布尔超立方体上具有相同的值，这意味着这些值将是 h(X) 的 根。

最常见的是，这被陈述为：h(X) 在 {0,1}ᵛ 消失。

但是，为了证明 p(X) 和 q(X) 是相同的多项式，我们需要证明 h(X) 恒等于 0 ——也就是说，它的表达式为 h(X) = 0。

现在，由于 h(X) 是多线性的，因此它在每个变量中的次数最多为 1——因此其总次数最多为 v。 正如我们已经知道的那样，次数为 v 的非零多项式最多可以有 v 个根。

但是…… 我们声称 h(X) 有 2ᵛ 个不同的根！

这是不可能的：2ᵛ 大于 v (对于任何 v ≥ 1) (。 除非，当然，我们允许 h(X) 为 零多项式！

因此，这里唯一的可能性是 h(X) = 0，这反过来意味着 p(X) = q(X)。 因此，MLE 是唯一的，并且正是我们构建的表达式。

很棒，不是吗？

请，停止吧……

唯一性很重要，因为它 防止伪造。 通过这种方式，我的意思是如果存在多个可能的扩展，则作弊的证明者可能会尝试构建一个以满足其不正当需求。

但是使用 MLE，只有 一个正确的扩展。 扩展过程免费获得保护：唯一性意味着作弊者没有回旋余地！

计算 MLE

好的！ 我们已经证明了 MLE 是唯一的且定义明确的。 但是我们需要解决另一件事：实用性。

让我们快速回顾一下我们的公式：

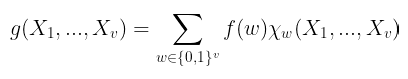
$g(X_1, …, Xv) = \sum{w \in \{0,1\}^v} f(w) \chi_w(X_1,…,X_v)$

请注意，我们正在对 2ᵛ 个元素求和，并且每个 χ 项都涉及 v 个乘法。 粗略地说，对 g 中的 单个点 进行求值总共需要 O(v.2ᵛ) 个操作。 如果我们不小心使用这些扩展，计算成本可能会 爆炸，从而导致 MLE 不切实际。

幸运的是，有一种巧妙的优化方法可以计算 MLE，从而大大缩短了评估时间，而这最终使这些小家伙非常有用。

这个技巧再次与我们可以利用的 递归结构 有关。 这里的一个例子将有助于概念化总体思路。

假设我们要计算某个 3 变量函数 f 的扩展 g(X₁, X₂, X₃)。 每个变量都是 二进制 的事实使我们能够以这种方式编写 g：

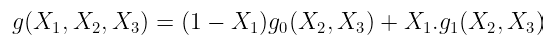
$g(X_1, X_2, X_3) = (1 — X_1)g_0(X_2, X_3) + X_1.g_1(X_2, X_3)$

其中 g₀ 和 g₁ 分别是原始函数 g 在 X₁ = 0 和 X₁ = 1 处的 限制。

通过使用这些限制，我们将原始 MLE 的求值 分解 为 两个较小的 MLE 的求值！ 当然，我们不需要停在那里：我们现在可以获取 g₀ 和 g₁，然后执行 完全相同的事情，从而将其求值减少为两个变量少一个新的 MLE。

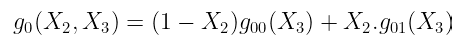
$g_0(X_2, X_3) = (1 — X2)g{00}(X_3) + X2.g{01}(X_3)$

一旦我们获得了一元多项式，它们的求值就会变得非常简单：

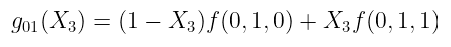
$g_{01}(X_3) = (1 — X_3)f(0,1,0) + X_3f(0,1,1)$

请记住：当我们计算多线性扩展时，X₃ 以及其他变量将从 有限域 中取值，而不仅仅是 0 和 1！

因此，为了计算 g，我们必须沿 相反的方向 行进。 我们从 f 的求值开始，然后对它们进行 组合。 按照我们的示例，将导致此处的小图：

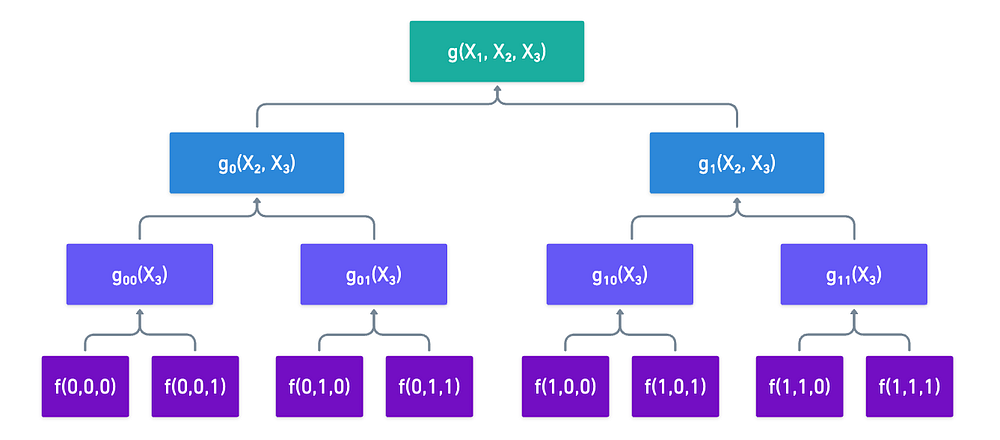
当我们考虑使用这些 MLE 的上下文时，就会发生神奇的事情。 你看，在我们优秀的 sum-check 协议中，我们需要在后续轮次中在以下各点计算 g：

• g(0, 0, 0), g(0, 1, 0), g(0, 0, 1), g(0, 1, 1), g(1, 0, 0), …
• g(r₁, 0, 0), g(r₁, 1, 0), g(r₁, 0, 1), g(r₁, 1, 1)
• g(r₁, r₂, 0), g(r₁, r₂, 1)

如果你需要，请再次查看协议！

在每一轮中，一个变量被固定为挑战值 r，但是剩余变量仍然采用 重复 且可以 重用 的布尔组合。

我们可以在我们的小示例中看到这一点。 假设我们需要找到 g(0,0,0)，然后找到 g(r₁,0,0)。 第一次评估提示我们计算 g₀(0,0) 和 g₁(0,0)：

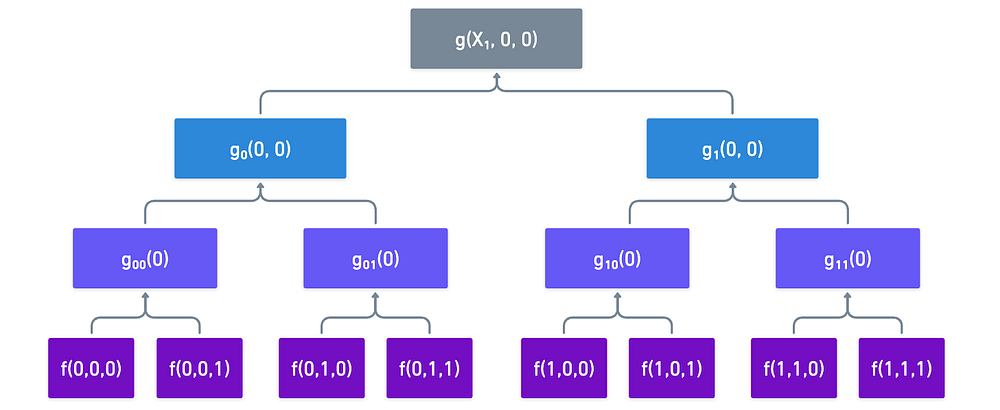
如果我们 存储 这些值以供以后使用，则当我们被要求计算 g(r₁,0,0) 时，我们可以简单地重用它们：

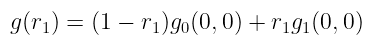
$g(r_1) = (1 -r_1)g_0(0,0) + r_1g_1(0,0)$

我们所做的是使用了算法设计中最古老的技巧之一：备忘录化 (memoization)！

我们所做的只是在开始sum-check时存储 中间值，然后稍后简单地重用它们，从而大大降低了求值成本！

这种获得的效率主要有助于在sum-check协议期间保持 证明者的运行时 可管理，或者实际上，在以这种二进制方式编码数据的任何其他上下文中。

酷！ 我们现在已经介绍了 MLE 背后的绝大多数技巧。 但是在离开之前，我们需要谈论另一件小事，这恰好是我们将来会经常使用的基本原理。

Schwartz Zippel 引理

我们之前用来证明唯一性的见解——次数为 d 的非零多项式最多可以有 d 个根——实际上是一个更通用且强大的结果的特例，我们在整个系列中会多次使用它，称为 Schwartz-Zippel 引理。 现在是介绍它的最佳时机！

这是想法：如果 p(X₁, …, Xᵥ) 是一个在域 𝔽 上的总度数为 d 的 非零多项式，并且我们从 𝔽 中选择随机值 r₁, …, rᵥ，那么我们恰好落在根上的概率是多少？

这个值恰好是：

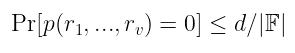
$\textrm{Pr}[p(r_1, …, r_v) = 0] \leq d / |\mathbb{F}\|$

只要 d 远小于有限域的大小，那么此概率就可以忽略不计！ 因此，如果我们选择一组随机输入，并且实际上得到 p(r₁, …, rᵥ) = 0，那么原始多项式是常数多项式 p(X₁, …, Xᵥ) = 0 的 机会非常大！

这似乎很简单，但实际上是一个非常强大的工具。 一个非常简单的应用是证明两个多项式是相同的：给定 p(X) 和 q(X)，我们可以将 h(X) 定义为：

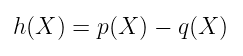
$h(X) = p(X) — q(X)$

当我们选择一个随机点 r*，并检查 p(r*) = q(r*) 时，我们实际上说 h(r*) = 0，这意味着 p(X) 等于 q(X) 的概率很高。

这应该非常让人联想到我们在sum-check 协议的 可靠性分析 期间使用的推理。 尽管我们没有明确说明，但我们使用了 Schwartz-Zippel 引理！

我们会经常使用它，所以一定要记住这一点！

总结

好的，这可能很多！ 让我们回顾一下今天学到的知识。

首先，布尔超立方体非常适合作为 索引策略。 我们可以利用它来编码信息，因为索引可以作为某个 函数 的输入，而我们想要编码的数据可以作为它的输出。

然后，为了在 sum-checking 中使用此函数，我们确定需要 扩展 它。 这就是我们得出 MLE 的方式：不再受布尔超立方体限制的这些函数的唯一扩展。

尽管我没有明确提到这一点，但是构建这些 MLE 非常容易。 我们使用的拉格朗日基非常简单。 出于这个原因，在扩展函数时，MLE 是更好的选择！

使用 MLE，我们可以获取几乎 任何数据集（一个数据库、一个向量、一个矩阵）并将其 编码为多项式，该多项式可以某种方式很好地与 sum-check 一起使用。

显然，还有一些我们尚未解决的问题：Sum-check 在所有这些中扮演什么角色？

我的意思是，编码数据很好，但是 计算 在哪里？

这就是 电路 的用武之地。 那将是我们的下一站，在那里事情最终会开始变得顺畅！

下次见！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～