Groth16 与证明你知道 x²-2x-15=0 的答案
- billatnapier
- 发布于 2025-11-18 16:50
- 阅读 705
本文介绍了非交互式零知识证明(NI-ZKP)的原理和应用,重点介绍了Groth16算法,它是第一个定义了恒定大小的证明并能有效验证的算法,并探讨了其在区块链中的实际应用。文章还提供了使用Groth16证明知道方程解的示例代码。
非交互式零知识证明的美妙之处
想象一下你是一位课堂上的老师,你要求你的学生找到方程 x²-2x-15=0 的根。但是,你不想教你的班级,你也不想计算出正确答案。为此,我们可以要求班级展示一个证明,证明他们知道正确答案,但实际上并不透露它。这就是非交互式零知识证明的魔力。
NI-ZKPs
我很荣幸能与这么多伟人交谈过,他们帮助保护我们的世界,无论是创建了至今仍在保护我们的密钥交换方法的 Whitfield Diffie 和 Marty Hellman,还是发明了椭圆曲线密码学的 Victor S Miller 和 Neal Koblitz。
虽然密钥交换和椭圆曲线方法为互联网提供了安全基础,但正是非交互式零知识证明 (NI-ZKPs) 让我们看到了现代魔法的发挥。为此,我们看到了 zk-SNARKs(简洁的非交互式知识论证)的兴起,通过它我们可以通过见证证明来证明对某事的了解。想象一下,我可以向你证明我住在某个地址,而无需实际告诉你该地址。
zk-SNARKs 的魔力
虽然 zk-SNARKs 早已被提出作为一个不错的理论概念,但 Groth16 是第一个定义了具有高效验证的恒定大小的证明,并且可以在链上区块链上实际实现。这使用了基于配对的密码学的魔法 [here][1]: 总的来说,通过 Groth16,我们信任特定于电路的设置,然后具有强大的知识假设,这为我们提供了现代 NI-ZKP 方法(如 STARK、PLONK 和 Halo)的开发参考点。
认识 Jens
所以,昨天,我很幸运赶上了 Groth16 的创造者:
https://www.youtube.com/watch?v=ooOYmDzoQj0
总的来说,Jens 专注于 NI-ZKP 领域,现在为 Nexus [here] 工作,该公司专注于将 ZKP 构建到Layer 1 区块链中。 Jens 在奥胡斯大学获得了博士学位,该大学是世界上一些最好的密码学研究的所在地,并且拥有像 Ivan Damgard 这样优秀的的研究人员 [here]: Ivan 发明了许多令人惊叹的密码学方法,但可能最出名的是他发明的与 MD5、SHA-1 和 SHA-256 一起使用的哈希方法:Merkle-Damgard (MD) 方法: 你可以在这里找到更多关于 Ivan 的信息。 获得博士学位后,Jens 曾担任伦敦大学学院的密码学教授,之后转任 Nexus 首席科学家。 对于 Jens 来说,学术界和工业界之间的跳跃是很自然的,而且似乎发生在他职业生涯的正确时机。
Groth16
用简单的方式解释 Groth16 并不容易,但我会尝试展示它如何集成到程序中。 第一个核心原则是使用基于配对的密码学,如果我们有两个曲线上的基点(U 和 V),我们有配对关系 (e()):
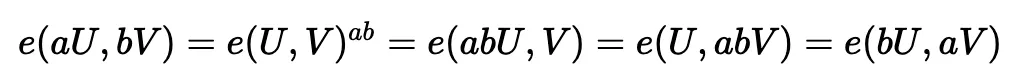
然后,点 a.U 和 bV 的配对与 ab.U 和 V 的配对相同。 所以,让我们举一个例子: x²-2x-15=0
这个的解是:
(x-5)(x+3)=0
所以 x=5 或 x=-3。 使用 Groth16,我们现在可以证明我们知道方程的答案,而无需实际展示我们的答案。 然后我们最初创建一个代表我们方程的电路:
circuit := cs.New()
// declare secret and public inputs
// 声明 secret 和 public 输入
x := circuit.SECRET_INPUT("x")
y := circuit.PUBLIC_INPUT("y")
// x^2+ax+b.
xval:= -3
yval:= 0
a:=-2
b:=-15然后可以用逻辑表示:
x3 := circuit.MUL(x, x) // x^2
x2 := circuit.MUL(a, x) // a.x
circuit.MUSTBE_EQ(y, circuit.ADD(x3, x2, b)) // x^2+ax+b然后我们定义什么是秘密的,并创建 Groth16 所需的 R1C2 电路:
good := cs.NewAssignment()
good.Assign(cs.Secret, "x", xval)
expectedY := cs.Element(yval)
good.Assign(cs.Public, "y", expectedY)
//.. circuit definition
//.. 电路定义
r1cs := cs.NewR1CS(&circuit)现在,我们可以创建一个 Proving Key 和一个 Verification Key:
var pk groth16.ProvingKey
var vk groth16.VerifyingKey
groth16.Setup(r1cs, &pk, &vk)然后我们创建一个证明,证明我们知道解决方案:
public := cs.NewAssignment()
public.Assign(cs.Public, "y", yval)
proof, err1 := groth16.Prove(r1cs, &pk, good)然后可以验证:
res,err2:= groth16.Verify(proof, &vk, public)
if (err2==nil) { fmt.Print("\nVerified: ",res) }完整的程序是 这里 :
package main
import
("github.com/consensys/gnark/cs"
"github.com/consensys/gnark/cs/groth16"
"fmt"
"os"
"strconv"
)
func main() {
// create root constraint system
// 创建根约束系统
circuit := cs.New()
// declare secret and public inputs
// 声明 secret 和 public 输入
x := circuit.SECRET_INPUT("x")
y := circuit.PUBLIC_INPUT("y")
// x^2+ax+b.
xval:= -3
yval:= 0
a:=-2
b:=-15
argCount := len(os.Args[1:])
if (argCount>1) {xval,_= strconv.Atoi(os.Args[1])}
if (argCount>2) {yval,_= strconv.Atoi(os.Args[2])}
if (argCount>3) {a,_= strconv.Atoi(os.Args[3])}
if (argCount>4) {b,_= strconv.Atoi(os.Args[4])}
fmt.Printf("%d =x^3 + (%d) x + (%d) when x= %d\n\n",yval,a,b,xval)
x3 := circuit.MUL(x, x)
x2 := circuit.MUL(a, x)
circuit.MUSTBE_EQ(y, circuit.ADD(x3, x2, b))
// circuit.Write("cubic.r1cs")
good := cs.NewAssignment()
good.Assign(cs.Secret, "x", xval)
expectedY := cs.Element(yval)
good.Assign(cs.Public, "y", expectedY)
//.. circuit definition
//.. 电路定义
r1cs := cs.NewR1CS(&circuit)
var pk groth16.ProvingKey
var vk groth16.VerifyingKey
groth16.Setup(r1cs, &pk, &vk)
public := cs.NewAssignment()
public.Assign(cs.Public, "y", yval)
proof, err1 := groth16.Prove(r1cs, &pk, good)
if (err1==nil) {
fmt.Print("Proof: ",proof)
} else {
fmt.Print("No proof!")
return
}
res,err2:= groth16.Verify(proof, &vk, public)
if (err2==nil) { fmt.Print("\nVerified: ",res) }
}你可以在这里尝试其他方程式:
- x=1, x ²−3 x −10=−12。 成功。尝试一下!
- x=1, x ²−3 x −10=−13。 失败。尝试一下!
- x=-3, x ²−2 x −15=0。 成功。尝试一下!
- x=5, x ²−2 x −15=0。 成功。尝试一下!
- x=4, x ²−2 x −15=0。 失败。尝试一下!
- x=-15, x ²+5 x −150=0。 成功。尝试一下!
- x=10, x ²+5 x −150=0。 成功。尝试一下!
- x=-8, x² +5 x −150=0。 失败。尝试一下!
这难道不是很棒吗?
如果你想了解如何设置 Groth,请在此处尝试: zkSnarks:从电路到验证 通过 zkSnark(一种非交互式自适应知识论证)
以及智能合约中的一个实际示例:
使用 Groth16 构建一个真实的 ZKP
一根绳子(string)有多长? 好吧,谁知道呢! 但是,创建和验证零知识证明需要多长时间? 好吧,这实际上是我们可以衡量的东西。 我们会发现,我们大约需要两分钟来生成证明,但我们可以快速检查证明是否正确。 总的来说,生成 ZKP 可能需要一段时间,但随后可以快速验证它。 由于我们想要良好的性能,我们将使用 Rust 编程语言来实现这一点,它将被编译成一个可执行程序。 一个常见的 ZKP 是 Groth16,它由 Jen Groth 在 2016 年创建 [1]。 这使用了基于配对的密码学并创建了一个简短的证明。 最好的 Rust 库之一是 Bellman 库。 在这里了解更多: https://learnblockchain.cn/article/22054
结论
与 Groth16 的创建者交谈真是太棒了,他开启了一个全新的机会世界,证明事物,而不会泄露我们的秘密。 在此处收听和观看。
参考文献
[1] Groth, J. (2016, April). On the size of pairing-based non-interactive arguments. In 年度密码技术理论与应用国际会议 (pp. 305–326). Berlin, Heidelberg: Springer Berlin Heidelberg.
- 原文链接: billatnapier.medium.com/...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 164 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 368 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 292 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 385 浏览
- 配对密码学之美:聚合签名和阈值签名 317 浏览
- 配对密码之美:聚合签名和阈值签名 560 浏览
- Zcash:比特币遗忘的隐私 436 浏览
- ZK编年史:计算模型 305 浏览
- lambdaworks 2026 年更新路线图和优先级 374 浏览
- 2026年构建机构级DeFi平台真正需要什么 919 浏览
- zkMesh:2026年1月回顾 460 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 657 浏览

