深入理解异步拜占庭共识

区块链技术的兴起让人们开始关注拜占庭共识协议（以下简称 BFT 协议）。在种类繁多的 BFT 协议中，异步 BFT 协议的鲁棒性最强，能够应对极端的网络环境。然而如何设计一种高效的异步 BFT 协议一直是学术界和工业界面临的难题。一直到 2016 年 Andrew Miller 等人提出了 Honey Badger BFT（简称 HB-BFT）才让人们看到异步 BFT 协议可以落地的潜力。近期比较火的 Dumbo（中文名”小飞象“）在 HB-BFT 的基础上进一步优化，极大提高了共识速度。本文主要以 HB-BFT[1] 和 Dumbo[2] 为例，深入探讨异步拜占庭共识所涉及的关键技术。

网络假设

拜占庭共识协议的设计和工程实现很大程度上依赖于对底层网络的假设。主要的网络假设有：

1. 同步（synchronous）网络假设网络中的消息能够在一个已知的时间 Δ 内到达，这是一种非常理想的假设，实际的工程实践中很难保证这一假设成立。
2. 半同步（partially synchronous）网络假设在一个 GST（global stabilization time）事件之后，消息在 Δ 时间内到达。随着网络技术的发展，这种假设已经能符合我们生活中遇到多绝大多数网络情况，而且设计和实现这类协议的难度不高，因此很多常见的协议比如 Paxos、Raft、PBFT 等都是基于半同步网络假设设计的共识协议。这些协议虽然能够保证在任何网络情况下系统的一致性，但在异步网络下会丧失活性。
3. 异步（Asynchronous）网络只保证消息最终能到达，并没有到达时间的限制，这几乎涵盖所有网络情况。由此可见，异步 BFT 协议的鲁棒性最强，即使在极端网络条件下协议也不会丧失活性。

我们将网络假设和容错模型作为两个维度可以将共识协议划分到下图所示的 6 个不同的象限，不同象限代表了不同的应用场景，最右下方的异步拜占庭场景对协议设计的要求最高。

之所以共识协议会出现这么多的分类都是为了绕过著名的 FLP 不可能定理：

reaching consensus in full asynchrony with a single process crashing is impossible with a deterministic protocol

FLP 定理从理论上证明了在纯异步环境下不可能存在一种确定性的共识协议。后世的研究者们为了绕过这个定理，不得不在两个方向上进行妥协：要么加强对网络的假设，要么引入随机源。

半同步共识 vs 异步共识

半同步共识协议就是基于第一种方法加强网络假设而设计的。这种方法可以让协议的设计相对简单，协议的关注点可以更多的放在安全性（safety），活性由 failure detector 来保证。比如在 PBFT 中，每个 replica 都要维护一个 timer，一旦 timeout 就会触发 view change 协议选举新的 leader。这里的 timer 就起到了一个 failure detector 的作用。由于半同步网络的假设存在，当网络恢复到同步之后，总能选出一个诚实的 leader，进而保证协议的活性。然而在异步环境下，failure detector 就会失去作用，可能导致无休止的 view change。除此之外，在工程实践中，即使底层网络能满足半同步假设的要求，但如何调节 timer 对协议的实际性能有非常大的影响。如果 timer 时间过短，那么可能导致 view change 频繁发生；如果时间过长，则可能导致网络从 partition 之后恢复较慢。

异步共识协议则完全不需要考虑 timer 的设置。为了保证协议的活性，异步协议需要引入随机源，简单来说就是当协议无法达成共识的时候，借助上帝抛骰子的方式随机选择一个结果作为最终结果。

Honey Badger BFT

下面以 HB-BFT 为例，讨论一下异步拜占庭共识所涉及的核心技术。异步拜占庭共识由于协议设计比较复杂、通信复杂度比较高，很长一段时间都只停留在论文中，直到 2016 年 Andrew Miller 在 CCS 上发表 HB-BFT 才意味着异步拜占庭容错正式迈入可实用领域。HB-BFT 通过非常巧妙的设计将整体的通信复杂度降低到了接近于最优的 O(|B|)，前提是区块所占带宽 |B| 足够大。

HB-BFT 通过模块化的方式解决了拜占庭环境下的原子广播（Atomic Broadcast，ABC）问题，即如何保证在异步和拜占庭环境下，各个节点按相同顺序收到相同的消息。HB-BFT 首先将 ABC 分解成一个核心模块，异步共同子集（Asynchronous Common Subset，ACS）。之后将 ACS 分解成了 RBC(Reliable Broadcast) + ABA(Asynchronous Binary Agreement)两个子模块，并且分别针对这两个子模块找到了两个比较优化的实现，如下图所示。接下来我们讨论每个模块是如何实现的。

HB-BFT

首先，我们看 HB-BFT 是如何利用 ACS 实现 ABC 的。简单来说，每个节点都参与贡献一个区块的一部分，而 ACS 的作用就是决定哪些节点贡献的这一部分最终达成了共识。HB-BFT 的流程如下图所示。

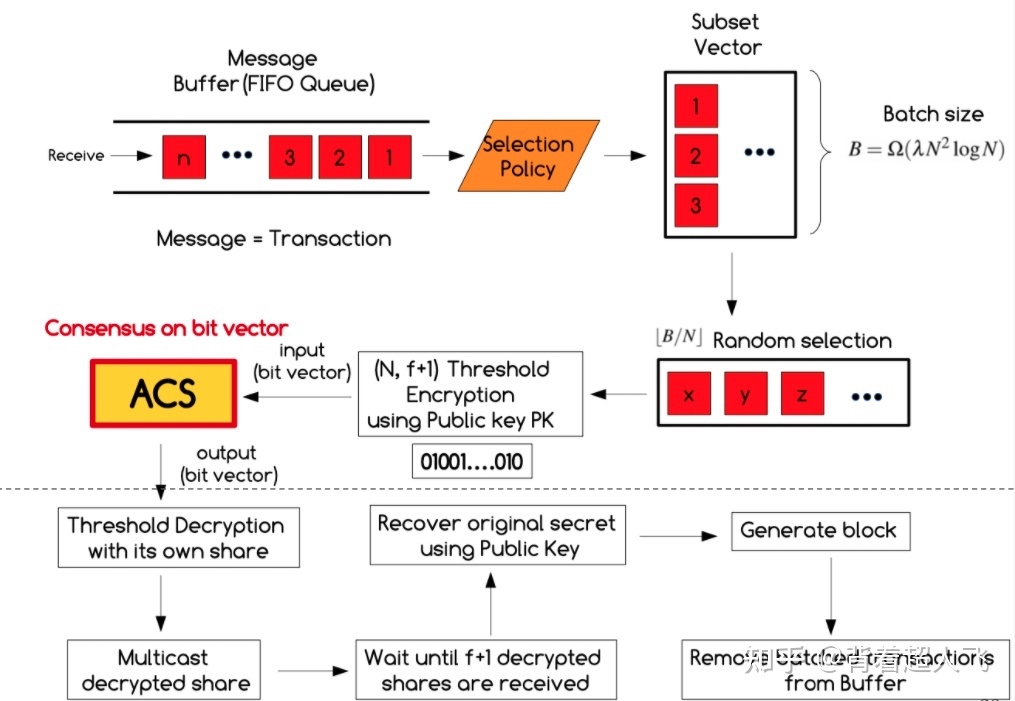
假如网络中一共有 10 个节点，每个节点维护了一个交易池作为接收来自客户端交易的缓冲池，每个区块包含 B = 100 个交易。

1. 每个节点首先从本地的交易池中选取前 100 个合法的交易，之后再从这 100 个交易中随机选择 100/10=10 笔交易作为自己的 proposal。这里之所以每个节点只选择 B/N 笔交易是为了降低通信复杂度，而之所以采用随机选取的方式，是为了降低每个节点选择重复交易的概率。
2. 通过一个共享公钥（阈值签名）将 proposal 加密，交易的内容直到共识结束后（收到了来自 f+1 个 share）才能被解密，从而防止了审查攻击（censorship attacks）。
3. 每个节点将加密后的 proposal 作为 ACS 模块的输入，输出就得到了一个“名单”，记录了有哪些节点提交的 proposal 成功得到共识。
4. 之后通过一系列的解密操作就得到了最终确认的区块。

ACS (Asynchronous Common Subset)

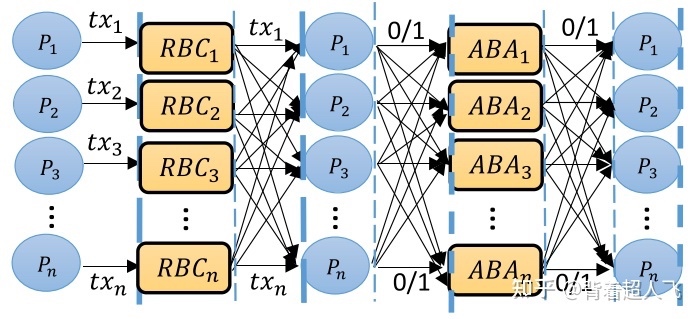
接下来我们讨论 HB-BFT 的核心——ACS 模块是如何实现的。ACS 可以被分解成 RBC(Reliable Broadcast) 和 ABA(Asynchronous Binary Agreement) 两个子模块。每个节点首先将本地的 proposal 通过 RBC 发送到其它节点，之后每个节点针对每个 RBC 的实例成功与否（0 或 1）执行一次 ABA。也就是说，每个节点都要并行运行 N 个 ABA 的示例（每个节点的 proposal 一个），每个 ABA 的输出 0 或 1 表示是否所有正确节点都认为这个 proposal 最终应该成为区块的一部分。

ACS 的运行流程如下图所示。假如一共有 N=10 个节点（最多容忍 f=3 个拜占庭节点），以节点 $P_1$为例。如果$P_1$ ​​收到来自$P_2$的 proposal（即 RBC2​ 成功），则 $P_1$将 ABA2​ 的输入置为 1。当$P_1$​​收到 N−f 节点的 proposal 时，将其它所有的 ABA 的输入都置为 0。直到所有 ABA 运行结束，将所有输出为 1 的 ABA 的汇聚成一个集合作为 ACS 的最终输出。例如，针对节点$P_1,P_3,P_4,P_6,P_7,P_9,P_10$发布的 proposal 对应的 ABA 的结果如果是 1 的话，ACS 的最终输出可以是（1，3，4，5，6，7，9，10）。ACS 保证所有正确节点都得到相同的输出。

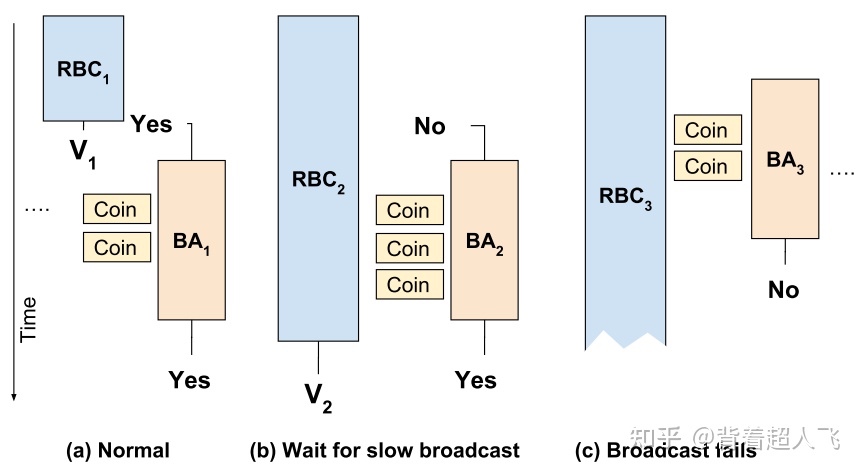
下图展示了 ACS 在执行过程中的三种情况。在正常情况下，RBC1 结束比较早，相对应的 ABA1​ 的输入为 1（yes），其输出也是 1。第二种情况，RBC2 结束的比较慢，在相对应的 ABA2​ 开始的时候（其它 N-f 个 RBC 成功之后）RBC2​ 还未结束，ABA2​ 的输入为 0（No），但由于其它 N-f 个节点对于 ABA2​ 的输入为 1，最终 ABA2​ 的输出也是 1，同时保证节点能够最终收到 RBC2​ 的 proposal。第三种情况，RBC3​ 失败，当其它 N−f 个 RBC 成功之后，节点对 ABA3​ 的输入为 0，最终 ABA3​ 的输出也是 0。

RBC (Reliable Broadcast)

可靠广播 RBC 可以确保源节点能够可靠地将消息发送到网络中的所有节点。具体来说，RBC 主要有以下三个性质：

• 一致性（Agreement）。任意两个正确节点都收到来自源节点的相同的消息。
• 全局性（Totality）。只要有一个节点收到了来自源节点的消息，那么所有正确的节点最终都能收到这个消息。
• 可信性（Validity）。如果源节点是正确的，那么所有正确的节点收到的消息一定与源节点发送的消息一致。

抗拜占庭的 RBC 最早由 Bracha 于1987年首次提出，并得到了广泛应用，其消息传递的示意图如下。RBC 主要分成 Initiate、Echo、Ready 三个阶段，其中后两个阶段各经历一次 all-to-all 的广播，因此 Bracha 的 RBC 协议的通信复杂度是$O(N^2|v|)$ 。

在这之后，Cachin 等人在 2005 年提出了基于纠删码的 RBC 实现，将通信复杂度降低到了$O(N|v|+\lambda N 2 \log N)$ 。HB-BFT 就是采用了这种优化的 RBC。当$|v|$远大于$\lambda N \log N$的时候，其通信复杂度可以近似表示为$O(N|v|)$ 。由于$|v|=|B|/N$，则 HB-BFT 整体的通信复杂度可以表示为$O(|B|)$（|B|为整个区块的大小），也就是渐进于理论最优。

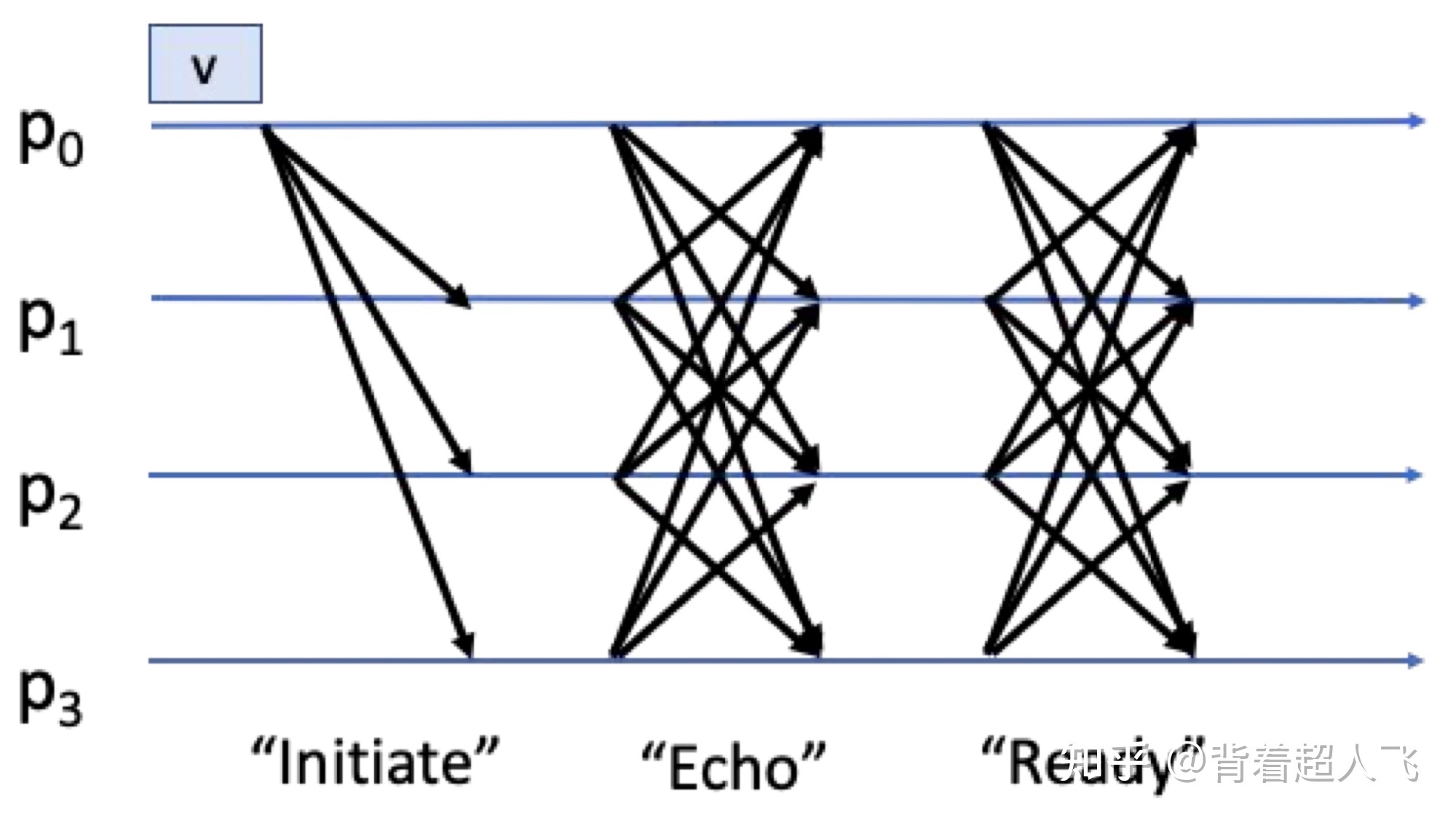
HB-BFT 中采用了基于(N-2f，N)的纠删码模式，即将一个数据块进行编码后，可以将其分成 N 份，其中只要任意 N-2f 份组合可以恢复整个数据块。消息传递的模式仍然跟传统的 RBC 类似。

ABA (Asynchronous Binary Agreement)

异步二元共识就是要在异步环境下让所有节点对于 0 或 1 达成共识。在 HB-BFT 中，每个节点都会针对其他所有节点的 RBC 是否成功进行一次二元共识，也就是说，每轮共识都要并行地执行 N 个 ABA 的实例。

ABA 主要满足下面几个性质：

• 一致性（Aggreement）。所有节点的输出相同（要么都是 0，要么都是 1）。
• 最终性（Termination）。如果所有正确节点都收到了输入，那么所有正确节点最终都会得到输出。
• 可信性（Validity）。如果任意正确节点的输出是 b（0 或 1），那么至少有一个正确节点的输入是 b。

ABA 的实现原理就是当节点无法达成一致的时候借助一个外部的随机源做决定。这个随机源就是 ABA 的核心组件（Common Coin，CC），我们也可以将 CC 理解成上帝掷骰子，只不过这个骰子只有 0 和 1 两个值。虽然只掷一次骰子可能还是无法达成共识，那么就不停掷，最终会出现所有人都达成一致的结果。Common Coin 有很多实现方案，HB-BFT 针对其模块化的设计，采用了基于阈值签名的 CC 方案。每个节点对一个共同的字符串进行签名并广播给其它节点，当节点收到来自其它 f+1 个节点的签名时，就可以将这些签名聚合成一个签名，并将这个签名作为随机源。

HB-BFT 性能测试

接下来我们看看 HB-BFT 的性能表现。作者们给出了 Python 版本的实现[3]，节点部署在广域网，分布在五个大洲，每个交易大小为 250 字节，总结点数 N = 4f，其中 f 为故障节点数，不考虑拜占庭行为。

我们首先看通信复杂度 vs batch 大小的实验结果，如下图所示。我们可以清楚地看到，当 batch size 逐渐增大的时候，每个节点的通信开销逐渐逼近线性增长。

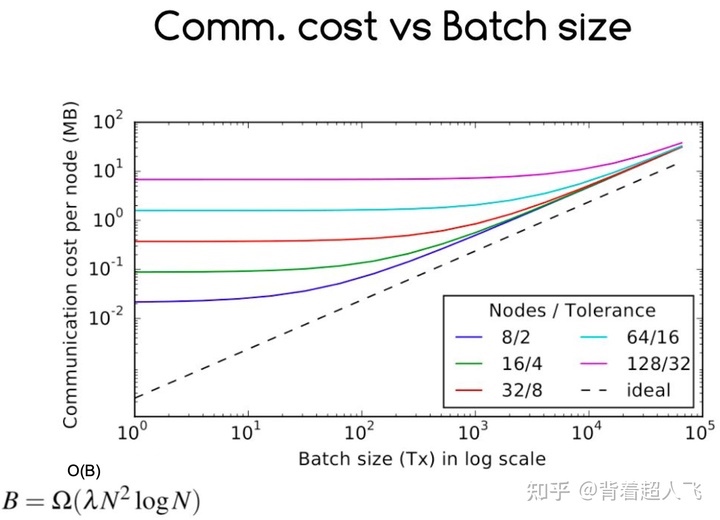
接下来我们看 HB-BFT 跟 PBFT 吞吐量的对比，如下图所示。我们可以看到在节点数为 8、16 的时候，两者差别不大，但随着节点个数增加，PBFT 的吞吐量有明显下降，而 HB-BFT 则几乎没有什么变化。这是由于 PBFT 是由 leader 将区块发布给其他节点，当节点数增加的时候，leader 的带宽逐渐成为瓶颈，而 HB-BFT 则不存在 leader 的概念，每个节点都贡献区块的一部分，因此吞吐量受网络规模影响不明显。

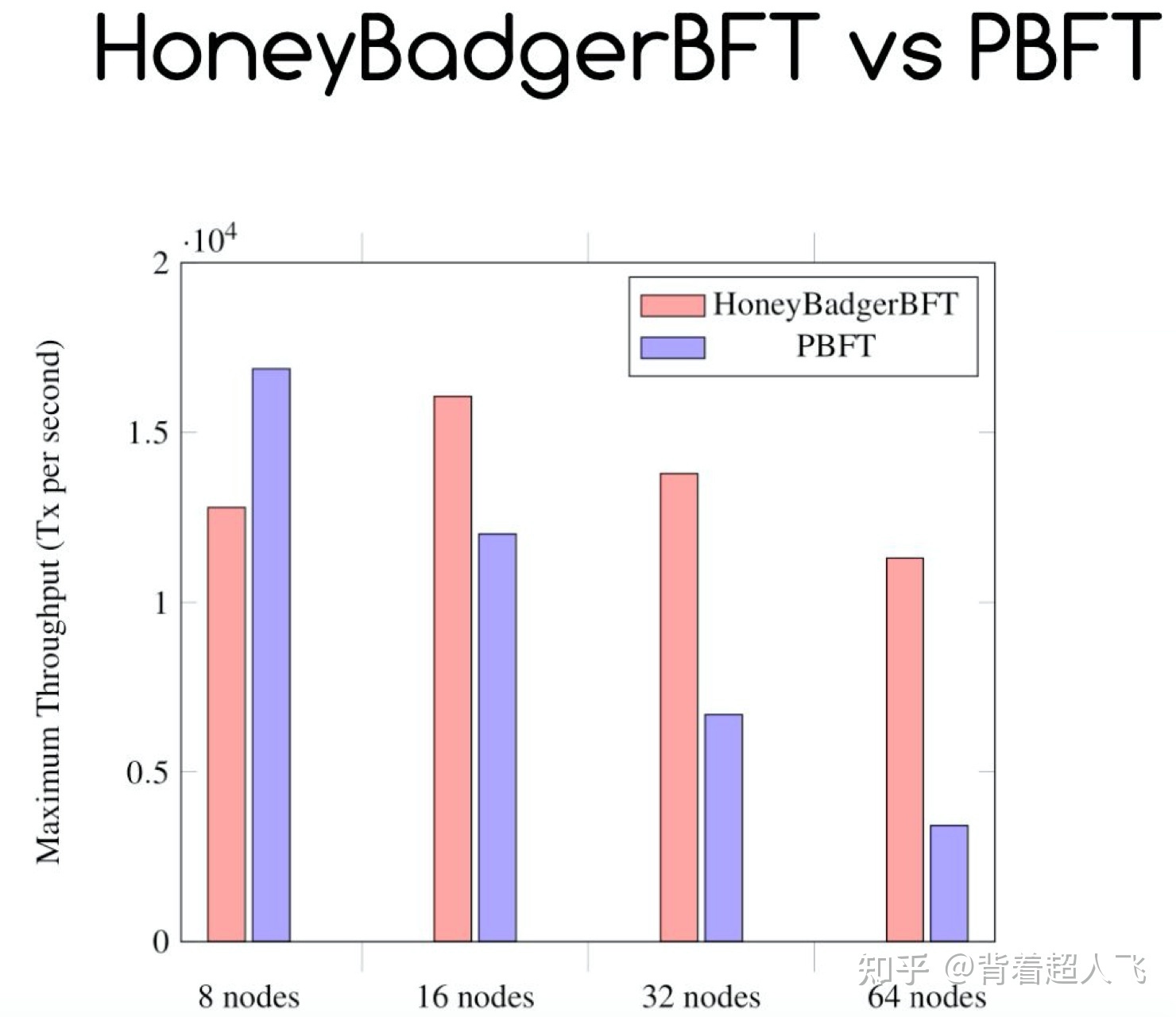
最后我们来看 HB-BFT 的吞吐量-延迟表现情况，如下图所示。我们可以明显看到，随着网络规模增加，协议的基础延迟明显增加。当网络规模达到 104 个节点的时候，协议的基础延迟增加到 600s。之所以协议的延迟对网络规模这么敏感是因为在每轮共识中，每个节点都要运行 N 个 ABA 的实例，而每个 ABA 的实例都要校验$O(N^2)$个阈值签名，因此计算复杂度非常高，随着网络规模增加，首先到达瓶颈的是 CPU，而不是带宽。接下来将要介绍的 Dumbo 就是在这个发现的基础上对 HB-BFT 的延迟进行了优化。

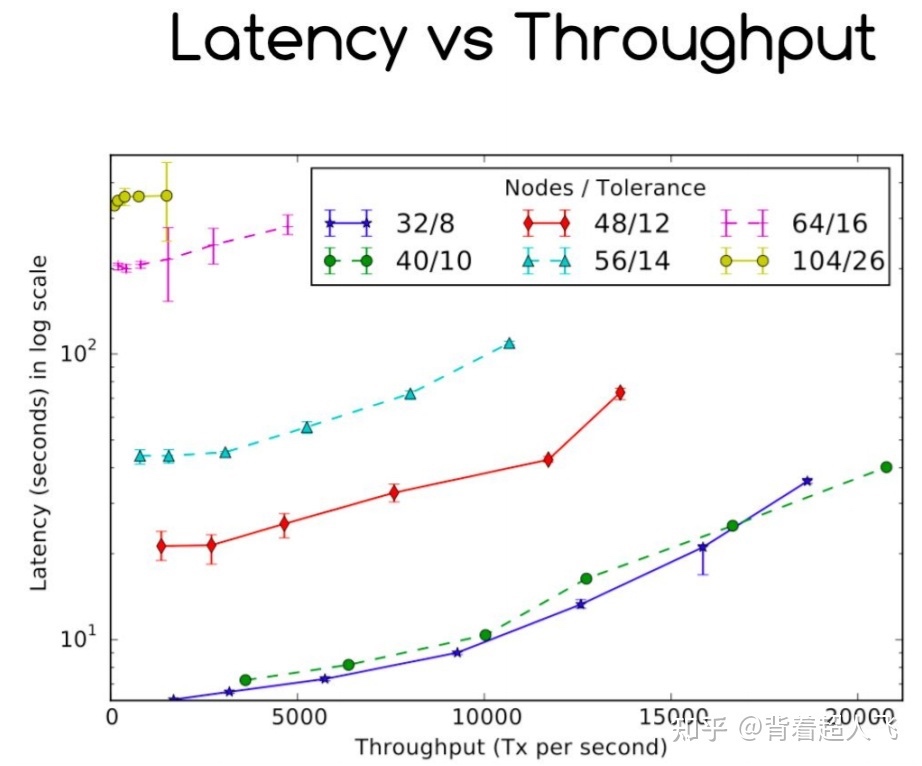
Dumbo: Faster Asynchronous BFT Protocols

聊完了 Honey Badger BFT，我们下面来聊一聊它的继任者 Dumbo（小飞象）。小飞象协议是来自新泽西理工的唐强教授联合中科院和京东创新实验室共同完成的。经过对 HB-BFT 性能的详细分析，Dumbo 的作者们发现影响 HB-BFT 性能的一个瓶颈是 ABA。由于在每轮共识中每个节点都要运行 N 个 ABA 的实例，每个实例都要验证$O(N^2)$个阈值签名，这对 CPU 的消耗很大。如下图所示，RBC 的运行时间相比 ABA 几乎可以忽略不计，而且随着 N 增大，运行 ABA 所需要的时间越来越长。

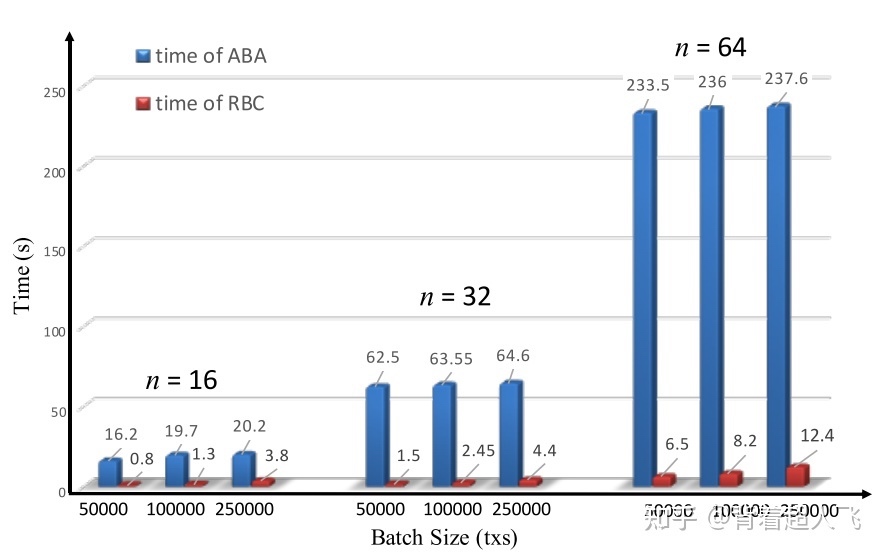
于是如何减少每轮共识中需要运行的 ABA 实例个数就是提高异步共识效率的关键。沿着这个思路，Dumbo 给出了两种解决方案，分别是 Dumbo1 和 Dumbo2。下面简单谈一下 Dumbo1 和 Dumbo2 的思路，具体细节和证明请看论文原文。

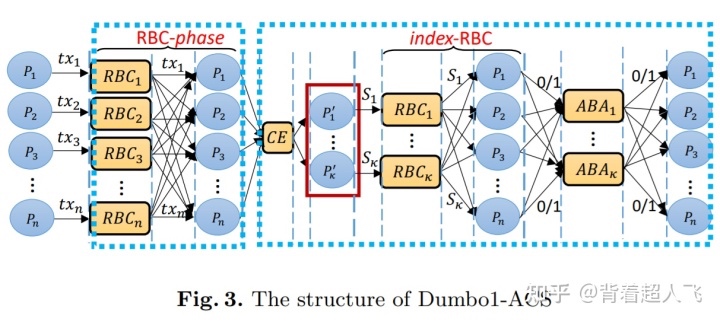
Dumbo1 的思路非常简单（如下图所示）：既然我们的目标是选取一个共同子集，那么为什么不选取一个由 k（k<N） 个成员组成的委员会，每个成员提议一个子集，这样我们只需要对每个提议进行一次二元共识不就可以了？这样就可以把运行 ABA 的实例个数从 N 减少到 k。于是 Dumbo1 的关键问题就转化成了如何随机选举一个 k 个成员组成的委员会，并且大概率能保证 k 个成员中至少有一个是诚实的。

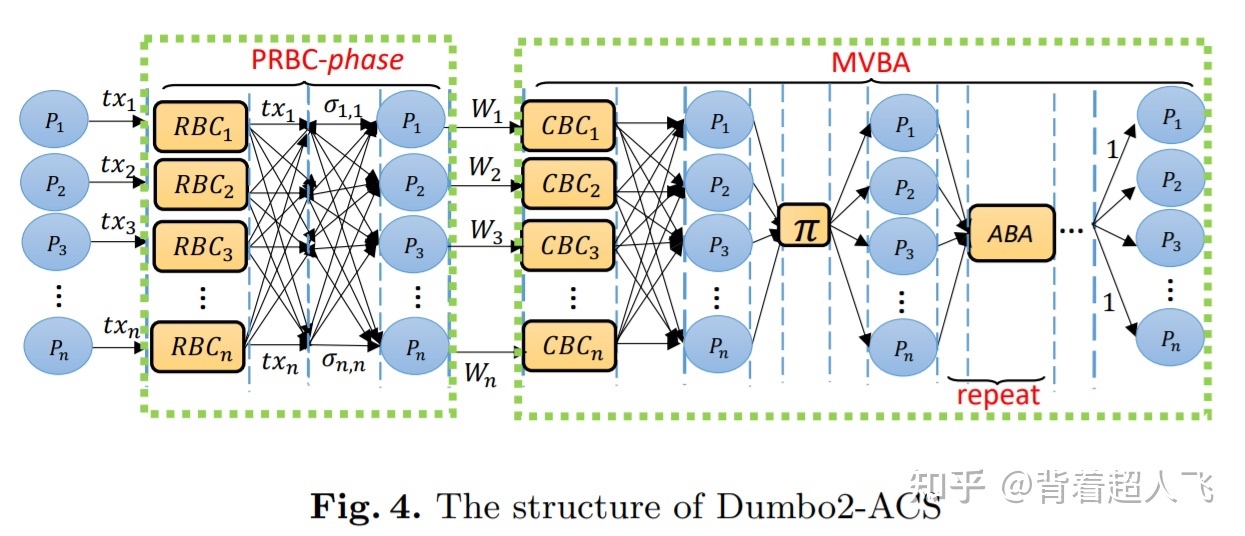
Dumbo2 的目标更为激进，能否将 ABA 的个数直接降到常数级别呢？有一个方法，就是使用多值拜占庭共识（Multi-value Validated Byzantine Agreement，MVBA），也就是说，我们能否让每个节点都提议一个子集（前提是这些提议要满足某个前提条件），然后从 N 个子集中选取 1 个作为共识结果（如下图所示）。问题在于，已有的 MVBA 的方案的通信复杂度较高，达到$O(N^2)|m|+ \lambda N^2 +N^3$，其中 |m| 为 MVBA 的输入的大小。由此可见影响 MVBA 通信复杂度的关键在于 |m| 的大小。如果 |m| 的值足够小，那么使用 MVBA（只包含常数级的 ABA 运行个数）实现 ACS 的效果就要远好于 HB-BFT 使用的 RBC 跟 ABA 的组合。Dumbo2 的解决办法就是尽可能缩小 |m| 的大小。

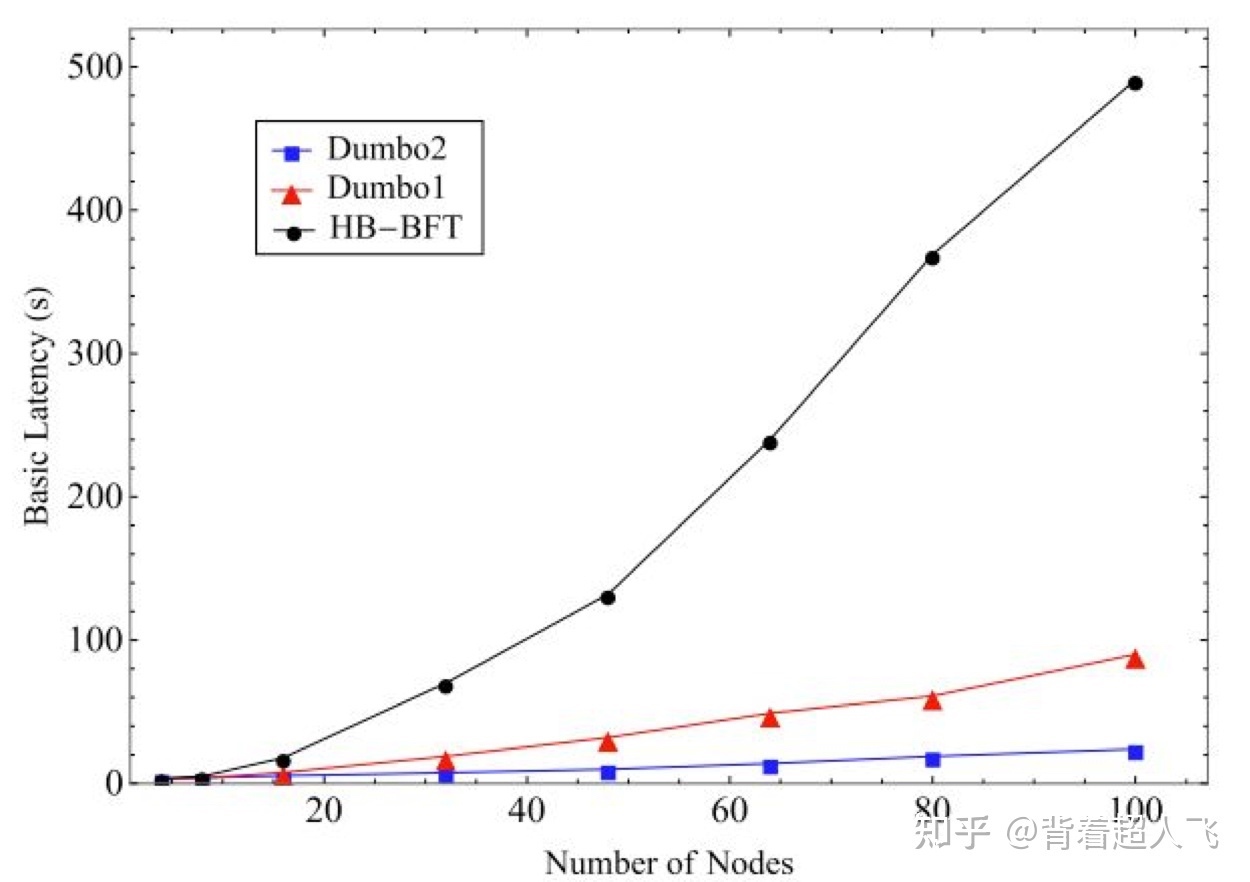
通过下图的实验结果我们可以看出 Dumbo1 和 Dumbo2 相比于 HB-BFT 的基础延迟提升明显。

总结

异步拜占庭协议由于其对极端网络环境的容忍度很高，非常适用于节点规模相对较大、网络环境不可预测的场景，比如跨多个地域的数据中心、无线网络、物联网等。这类协议虽然看起来非常复杂，但比较容易进行模块化的设计，在工程实践中仍然有很大的优化空间。

由于异步拜占庭协议理解起来不是那么直观，我在这里也只是走马观花地介绍了其中的核心技术。对这方面感兴趣的同学欢迎在下面留言或者私信我讨论。

参考文献

[1]The Honey Badger of BFT Protocols

[2]Dumbo: Faster Asynchronous BFT Protocols

本文首发于：https://zhuanlan.zhihu.com/p/362845060