零知识证明 - 椭圆曲线基础
- Star Li
- 发布于 2020-01-20 15:52
- 阅读 9439
有限域上的椭圆曲线是零知识证明的基础。零知识的实现是基于离散对数问题。从计算的角度来看,F_p是个有限域,在之基础上建立的椭圆曲线点的运算都是在这个域范围内。有限域上的椭圆曲线上有很多循环子群F_r,具有加法同态的特性。离散对数问题指的是,在循环子群上已知两点,却很难知道两点的标量。
年底了,有点忙。忙着给自己2019年做标记,忙着和小伙伴聚聚餐,谈谈创业,谈谈今年的状态。手头的产品也在打磨。区块链技术是个有趣的行业,爱并痛着。上个星期,自己把零知识证明证明的理解梳理了一下,也尝试直播五天分享我的理解。直播非常好玩,Zoom直播性能不错。感受比较深的是,像这样需要比较繁杂的理论基础的知识不太好讲,很多人在听了第一天之后都撤了。也非常感谢和我一起坚持到最后的小伙伴,更要感谢加入零知识证明技术星球的小伙伴,你们的陪同给我很大的动力。
做技术的小伙伴,一定要注意底层理论的积累,虽然底层理论学习貌似枯燥无味,却能让你能进行更高效率的证明或者推演。
对椭圆曲线的学习,个人推荐如下的链接,没有太多的术语,解释的比较清楚。
-
https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/ 中译文:https://learnblockchain.cn/article/8731
本文也是在上述链接的基础上的总结。
1. 实数域上的椭圆曲线
1.1 定义
椭圆曲线的数学定义可以查看Wolfram MathWorld。不是密码学或者数学专业的小伙伴,看的是一头雾水。便于工程理解,椭圆曲线是一系列满足如下方程的点:
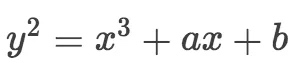
并且 $4a^3+27b^2\neq0$。该方程称为椭圆曲线的Weierstrass方程。
如下是b=1, a从2到-3的椭圆曲线:

从方程可以看出,椭圆曲线是关于x坐标对称的曲线。除了坐标系上曲线的点,椭圆曲线额外定义一个点(无穷远处),记为 0。
也就是说,椭圆曲线是由如下的点组成:
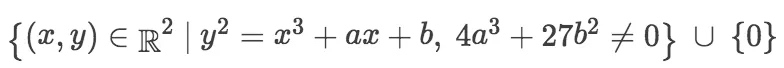
1.2 基于椭圆曲线的群定义
在椭圆曲线的基础上,可以定义一个加法群:
- 所有椭圆曲线上的点,就是这个群里的元素
- 单位元就是0
- 点P的逆元是点P相对x坐标的对称点
- 加法定义如下:在椭圆曲线上,和一条直线相交的3个点P,Q以及R,三点相加满足。也就说,椭圆曲线上的两点相加的结果,还在椭圆曲线上。
结合群的定义,可以证明定义的这个加法群,就是阿贝尔群。
- 封闭性:因为椭圆曲线上的点相加,还是椭圆曲线上的点。
- 结合律:P+(Q+R)=(P+Q)+R=0
- 单位元: 单位元是0
- 逆元: 一个椭圆曲线上的点P的逆元,是相对x坐标的对称点
- 交换律:P+Q=Q+P
1.3 椭圆曲线加法计算
因为 P+Q+R = 0,也就是 P+Q = -R。计算 P+Q 的方法就比较直观了:连接P和Q划一条线,该线和椭圆曲线交的另外一个点为R。P+Q 的结果就是R的逆。
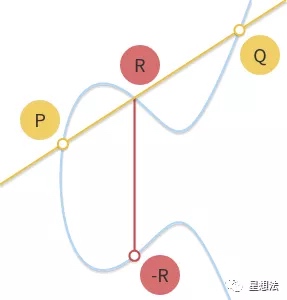
考虑几种特殊情况,对加法计算进行“修正”:
- P+0 或者 Q=0 :因为定义0为无穷远处,不能基于无穷远处划线。但是因为定义了0为单位元,所以 P+0=P 以及 0+Q=Q。
- P = -Q :因为两个点是对称的,所以基于这两个点划的线垂直于x轴,不再相交于其他点。P+Q = -Q+Q = 0。
- P = Q :如果P和Q是同一个点的话, 那存在多条线穿过这“两个”点。如果把Q看作是无限接近P的过程,可以看出,穿过P和Q的是椭圆曲线在P点的切线。如果切线和椭圆曲线相交的点为R,则 P+P+R = 0,P++ = 2P = -R 。
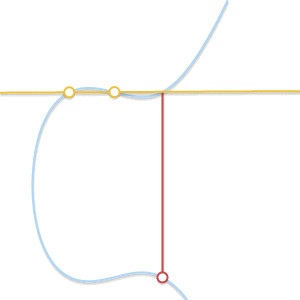
- P ≠ Q,并且不存在第三个点相交:这种情况和上一种情况有点类似,也就是说,P/Q的连线是椭圆曲线的切线。如果P点是切点,P+P+Q = 0。也就是说,P+Q = -P。
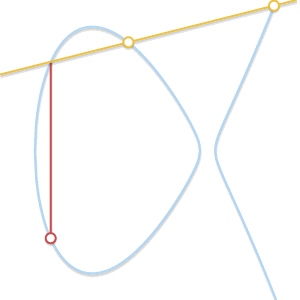
1.4 加法计算推导
加法的定义是完备的。针对最普通的情况,就是在椭圆曲线上一条直线能穿过三个点,分别是P,Q。$P=(x_P,y_P)$ ,$Q=(x_Q,y_Q)$,$R=(x_R,y_R)$。这条直线有个斜率:
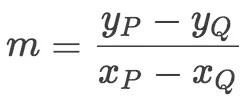
可以推导出:
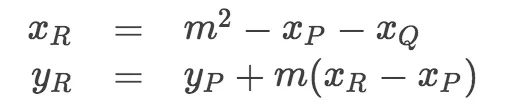
或者
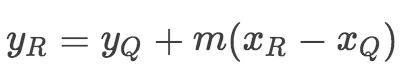
当然,如果P/Q是同一个点的话,斜率的计算公式不同。
1.5 标量乘法(Scalar Multiplication)
在加法的基础上,定义了标量乘法,同一个点相加多次:
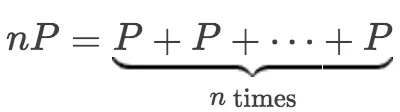
计算标量乘法,最简单的方法是一个个P点相加。如果n是k位的话,算法复杂度是:$O(2^k)$。
有个快速的计算方法:double后相加。假设n=151,二进制表示为:</sub>10010111<sub>2。
还是用n=151举个例子:
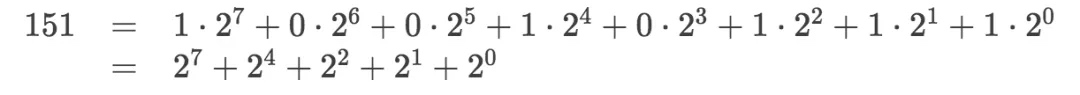
"Double"主要是依次获得某个位对应的变量的结果。如果该位是1,就加到最后的结果中。这种算法的复杂度是:O(k)。
1.6 对数问题
已知n和P,Q = nP 的计算比较容易。但是,在Q和P已知的情况下,求解n非常困难,没有多项式时间求解算法。
2. 有限域上的椭圆曲线
上面介绍的是基于实数的椭圆曲线的点,可以构造一个群。考虑特征数为的有限域,为素数。该有限域是由模的结果组成,记$F_p$。因为有限域中的元素都有逆元,也就是$x\cdot x^{-1} = 1$,则$x/y = x\cdot y^{-1}$。
2.1 扩展欧几里得定理
给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。gcd(a,b)是最大公约数。
2.2 模p运算下的乘法逆
假设元素a,在模运算下,有逆元x。满足,a·x = 1(mod p)。也就是说,
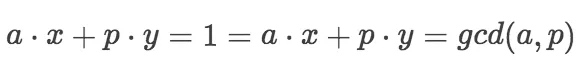
通过扩展欧几里得定理,可以求得x和y。x就是a的乘法逆。
2.3 在F_p定义椭圆曲线
在$F_p$上椭圆曲线定义如下:
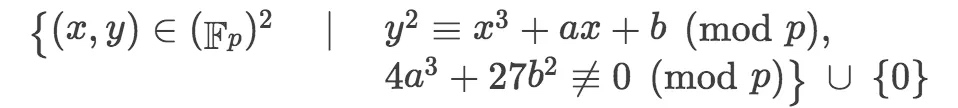
定义和实数上的定义类似。如下是$y^2\equiv x^3-7x+10(mod\ p)$,p分别是19,97,127,487对应的椭圆曲线的点。
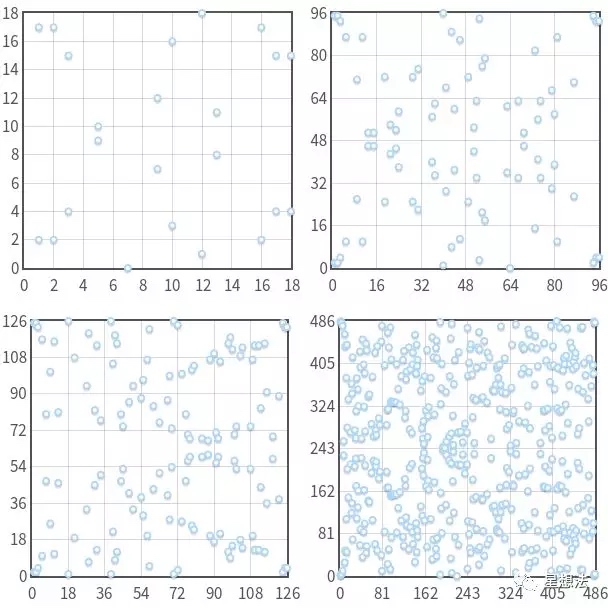
椭圆曲线是关于 y = p/2 对称,因为
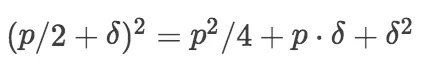
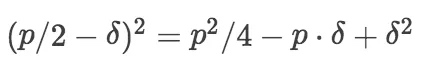 在模p的情况下,这两个等式相等。
在模p的情况下,这两个等式相等。
2.4 点加
和实数上椭圆曲线的点加类似,定义在一条“线”上的三点相加等于0:P+Q+R = 0 。在$F_p$有限域上,一条直线定义为:$ax+by+c \equiv 0(mod\ p)$。
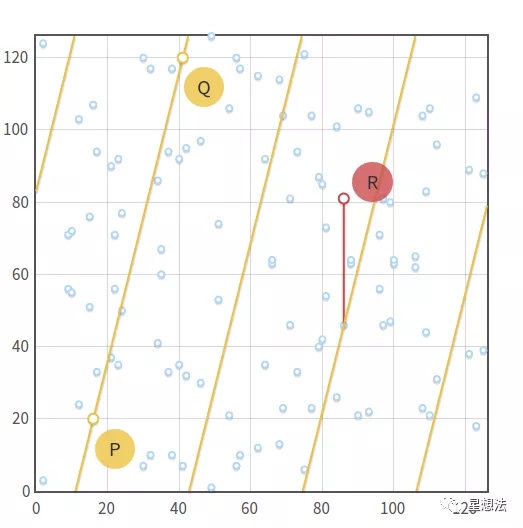
上图是$y^2\equiv x^3-x+3(mod\ 127)$的椭圆曲线,其中P = (16,20) , Q = (14,120) 。图中的黄色的一系列的斜线是 $y\equiv 4x+83(mod\ 127)$的直线。R就在其中一条斜线上,-R就是图中标出的R的对称点,也就是P+Q的结果。
点加性质: · Q+0 = 0+Q = Q · $-Q=(x_Q,-y_Q\ mod\ p)$, 也就是,-Q是横坐标相同但纵坐标相反的点,也就是,相对p/2对称的点。 · P+(-P) = 0
2.5 点加计算
假设三个点在一条线上,$P=(x_P,y_P)$,$Q=(x_Q,y_Q)$,$R=(x_R,y_R)$。如果P和Q不是同一个点:
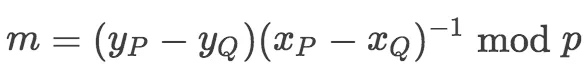 从而,推导出:
从而,推导出:
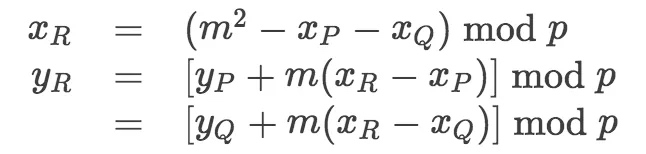 其他条件下的推导,涉及的公式比较多。有兴趣的小伙伴可以自行推导。
其他条件下的推导,涉及的公式比较多。有兴趣的小伙伴可以自行推导。
2.6 在有限群上的椭圆曲线有多少点?
椭圆曲线上的点的个数,称为“阶”。如果枚举0~p-1,查看点的个数,不太现实,因为p是一个非常大的质数。Schoof算法能在多项式时间确定椭圆曲线阶:https://en.wikipedia.org/wiki/Schoof%27s_algorithm。
2.7 标量乘法
和实数域上一样,可以使用double后相加的方法计算。在有限域上,有额外的特性,举个例子:
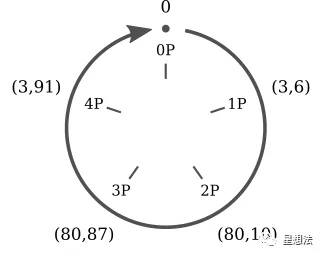
已知$y^2\equiv x^3+2x+3(mod\ 97)$以及点P = (3,6)。点P的标量乘法的结果是循环的,只有五个点。 0P = 0 1P = (3,6) 2P = (80,10) 3P =(80,87) 4P =(3,91) 5P = 0 6P = (3,6) 7P = (80,10) 8P = (80,87) 9P =(3,91) ... nP = (n%6)P
很容易看出,在有限域上的椭圆曲线中一个点标量乘法的结果,组成一个在加法操作下的循环子群。在子群中的点,所有的加法的结果都还在子群中。而且,存在一个点,幂次(加法操作)能生成子群中的所有点。这样的点,称为“生成元”。
绕了一大圈,在有限域上的椭圆曲线上,存在很多个循环子群。子群是基于加法操作。
2.8 循环子群的阶
Schoof算法能确定整个基于有限域上的椭圆曲线上的点的个数,但是不能确定循环子群的个数。 拉格朗日定理指出,对于任何有限群G,G的每个子群H的阶次(元素数)都会被G的阶次整除。
https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)
该定理给寻找循环子群的阶n,提供了一个思路:
1/ 利用Schoof算法,计算出整个椭圆曲线的阶
2/ 找出其所有的约数
3/ 找出最小的约数n,满足 nP = 0
2.9 寻找生成元
通常使用椭圆曲线算法,先选择曲线,计算椭圆曲线的阶,然后在这条曲线上找到最大的子群。找子群,就是寻找子群对应的生成元。
假设椭圆曲线的阶为N,子群的阶为n,由拉格朗日定理,h = N/n。
又因为椭圆曲线的阶为N,P为椭圆曲线上的随机的点,存在 NP = 0。也就是说 n(hP) = 0。
则 G = hP 为子群的生成元。
2.10 离散对数问题
已知两个在子群上的点P和Q,求解 Q = kP 是非常难的问题。目前该问题没有多项式时间求解算法。
2.11 同态
如果子群的阶为r,则 Q = (k%r)P 。
同态加法:
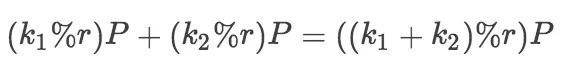
总结:
有限域上的椭圆曲线是零知识证明的基础。零知识的实现是基于离散对数问题。从计算的角度来看,F_p是个有限域,在之基础上建立的椭圆曲线点的运算都是在这个域范围内。有限域上的椭圆曲线上有很多循环子群F_r,具有加法同态的特性。离散对数问题指的是,在循环子群上已知两点,却很难知道两点的标量。
我是Star Li,我的公众号星想法有很多原创高质量文章,欢迎大家扫码关注。

- ZK编年史:哈希登场 148 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 362 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 286 浏览
- 以太坊签名方案解析:ECDSA、BLS、XMSS 以及带 Rust 代码示例的后量子 leanSig 366 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 372 浏览
- Zcash:比特币遗忘的隐私 434 浏览
- 论“高保证”密码学的承诺 308 浏览
- ZK编年史:计算模型 301 浏览
- lambdaworks 2026 年更新路线图和优先级 365 浏览
- 2026年构建机构级DeFi平台真正需要什么 909 浏览
- zkMesh:2026年1月回顾 452 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 645 浏览

