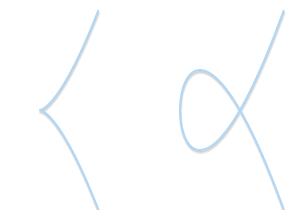椭圆曲线密码学 入门篇

翻译一篇来自 ANDREA CORBELLINI 经典的密码学文章： 原文：https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/

以下是原文翻译：

了解公钥密码学的人可能已经听说过ECC、ECDH或ECDSA。第一个是椭圆曲线密码学的缩写，其他两个是基于它的算法的名称。

今天，我们可以在 TLS、PGP和 SSH 等主要技术中找到椭圆曲线密码系统，这些技术是现代网络和 IT 世界的基础。更不用说比特币和其他加密货币了。

在 ECC 变得流行之前，几乎所有的公钥算法都是基于 RSA、DSA 和 DH 的，这些是基于模算术的替代加密系统。RSA 和相关算法今天仍然非常重要，并经常与 ECC 一起使用。然而，尽管 RSA 和相关算法背后的原理可以很容易地解释，被广泛理解，并且粗糙的实现可以相当容易地编写 ，但大多数人对 ECC 的基础仍然一无所知。

通过一系列博文，我将向你介绍椭圆曲线密码学的世界。我的目标不是提供关于 ECC 的完整详细指南（网络上关于这个主题的信息很多），而是提供对 ECC 是什么以及为什么被认为是安全的简单概述，而不浪费时间在漫长的数学证明或乏味的实现细节上。我还将提供有用的示例以及可视化交互工具和脚本供你使用。

具体来说，我将涉及以下主题：

1. 实数上的椭圆曲线和群定律（在本博文中讨论）
2. 有限域上的椭圆曲线和离散对数问题
3. 密钥对生成和两个 ECC 算法：ECDH 和 ECDSA
4. 破解 ECC 安全性的算法，并与 RSA 进行比较

为了理解这里所写的内容，你需要了解一些集合论、几何和模算术的基础知识，并熟悉对称和非对称加密。最后，你需要清楚地了解“简单”问题和“困难”问题是什么，以及它们在密码学中的作用。

准备好了吗？让我们开始吧！

椭圆曲线

首先：什么是椭圆曲线？Wolfram MathWorld 给出了一个优秀而完整的定义 。但对于我们的目的，椭圆曲线将简单地是由方程描述的点的集合：

$$ y^2 = x^3 + ax + b $$

其中 $$ 4a^3 + 27b != 0$$（这是为了排除奇异曲线）。上面的方程是椭圆曲线的Weierstrass 标准形式。

不同椭圆曲线的不同形状（b = 1，a 从 5 到 -5 变化）：

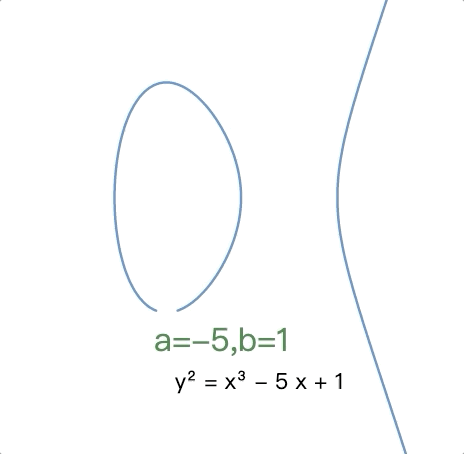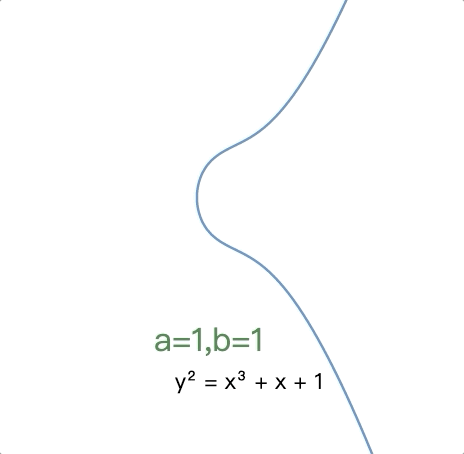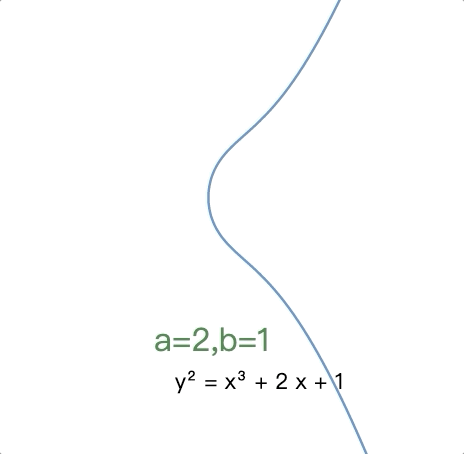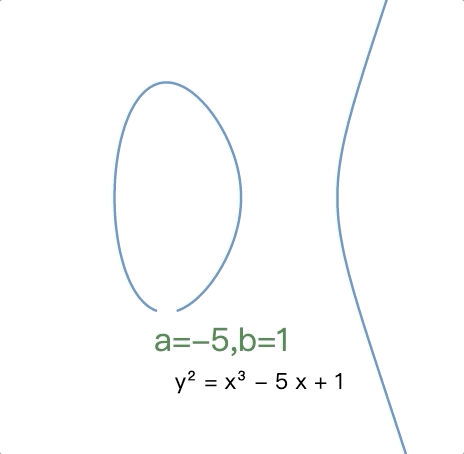
还可在 desmos 中 在线自行演示 。

奇点类型：左侧是具有尖点的曲线（$y^2 = x^3$）。右侧是具有自交点的曲线（$y^2 = x^3 - 3x + 2$）。它们都不是有效的椭圆曲线。

根据 $a$ 和 $b$ 的值，椭圆曲线在平面上可能呈现不同的形状。正如可以轻松看到和验证的那样，椭圆曲线关于 x 轴对称。

对于我们的目的，我们还需要一个无穷远点 （也称为理想点）作为我们曲线的一部分。从现在开始，我们将用符号 0（零）表示我们的无穷远点。

如果我们想明确考虑无穷远点，我们可以将我们对椭圆曲线的定义细化如下：

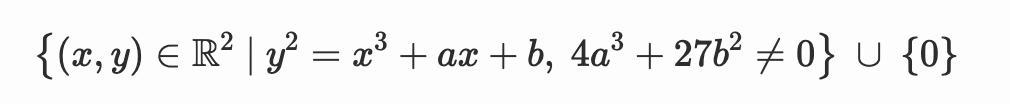
群(group)

在数学中，群是一个我们已经定义了一个称为“加法”的二元运算并用符号 + 表示的集合。为了使集合 $G$ 成为一个群，加法必须满足以下四个性质：

1. 封闭性(closure)： 如果 $a$ 和 $b$ 是 $G$ 的成员，则 $a + b$ 是 $G$ 的成员；
2. 结合律(associativity)： $(a + b) + c = a + ( b + c);$
3. 存在一个单位元(identity element) 0，使得 $a + 0 = 0 + a = a$;
4. 每个元素都有一个逆元(inverse)，即对于每个 a，存在 b 使得 $a + b = 0$。

如果我们添加第五个要求：

5. 交换律（commutativity）： $a + b = b + a $,

那么该群被称为阿贝尔群（abelian group）。

使用通常的加法概念，整数集合$Z$是一个群（而且是一个阿贝尔群）。然而，自然数集合$N$不是一个群，因为无法满足第四个性质。

群很好，因为如果我们可以证明这四个性质成立，我们将免费获得其他一些性质。例如：单位元 是唯一的；逆元也是唯一的，即：对于每个 a，只存在一个 b 使得$a + b = 0$（我们可以将 b 写为$-a$）。直接或间接地，关于群的这些以及其他事实将对我们以后非常重要。

椭圆曲线的群定律

我们可以在椭圆曲线上定义一个群，具体来说：

• 群的元素是椭圆曲线上的点；
• 单位元是无穷远点 0；
• 点 $P$ 的逆元是关于 $x$ 轴对称的点；
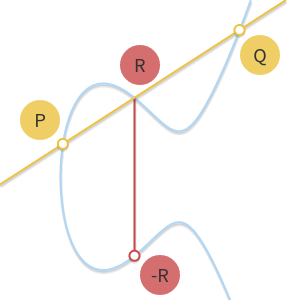
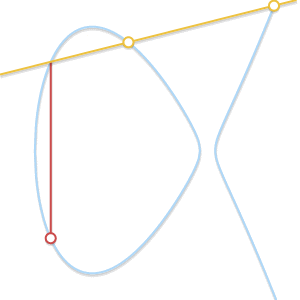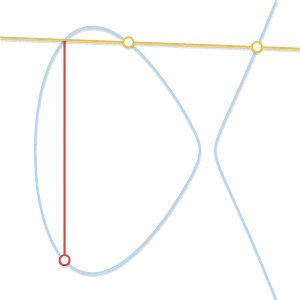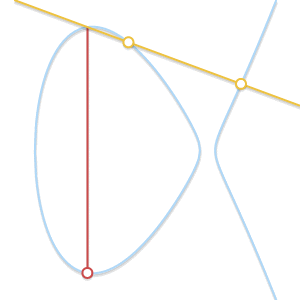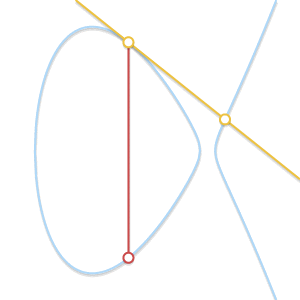
• 加法 由以下规则给出：给定三个对齐的非零点$P$、$Q$和$R$，它们的和是$P + Q + R = 0$ 。

三个对齐点的和为 0。

请注意，根据最后一个规则，我们只需要三个对齐的点，而三个点是无序的。这意味着，如果 P、Q 和 R 对齐，则$P +(Q + R) = Q + (P + R) = R + (P + Q) = ... = 0 $。这样，我们直观地证明了我们的+运算符既是结合的又是交换的：我们处于一个阿贝尔群中。

到目前为止，一切都很好。但我们如何实际计算两个任意点的和呢？

几何加法

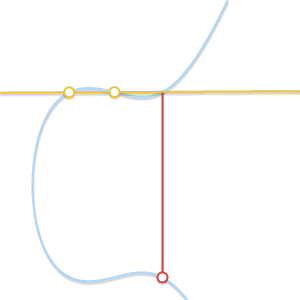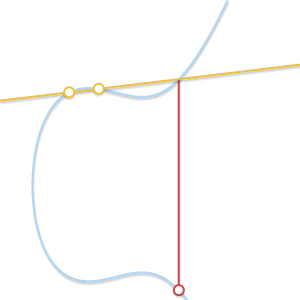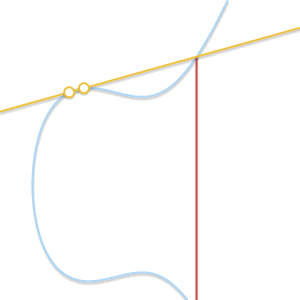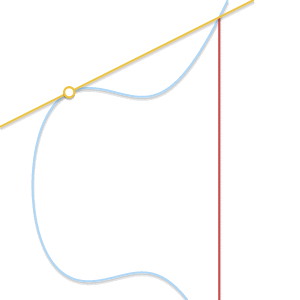
由于我们处于一个阿贝尔群中，我们可以将$P + Q + R = 0$写成$P + Q = -R$。以这种形式，这个方程让我们推导出计算两点$P$和$Q$之间的和的几何方法：如果我们画一条穿过$P$和$Q$的直线，这条直线将与曲线上的第三个点$R$相交（这是由于$P$、$Q$和$R$对齐的事实导致的）。如果我们取这一点的逆，$-R$，我们就找到了$P+Q$ 的结果。

画出通过 $P$ 和 $Q$ 的直线。该直线与第三个点 $R$ 相交。对称于该点的 $-R$， 是 $P + Q$ 的结果。

这种几何方法有效，但需要一些改进。特别是，我们需要回答一些问题： 如果 $P=0$ 或 $Q=0$ ? 当然，我们无法画出任何直线（0 不在 $xy$-平面上）。但鉴于我们已将 0 定义为单位元，对于任何 $P$ 和任何 $Q$，$P+0=P$ 且 $0+Q=Q$。

• 如果 $P=-Q$ ? 在这种情况下，通过这两点的直线是垂直的，并且不会与任何第三点相交。但如果 $P$ 是 $Q$ 的逆元，则根据逆元的定义，我们有 $P+Q=P+(-P) = 0$。

• 如果 $P=Q$ ? 在这种情况下，有无限多条通过该点的直线。这时情况开始变得有点复杂。但考虑一个点 $Q' \neq P$。如果我们让 $Q'$ 靠近 $P$，越来越接近它，会发生什么呢？

  

当这两个点越来越接近时，通过它们的直线变成切线。

当 $Q'$ 趋向于 $P$ 时，通过 $P$ 和 $Q'$ 的直线变成切线。基于此，我们可以说 $P+P = -R$，其中 $R$ 是曲线与切线相交的点 $P$。 如果 $ P \neq Q$，但没有第三个点 $R$ ? 我们处于与前一种情况非常相似的情况。实际上，我们处于通过 $P$ 和 $Q$ 的直线是曲线的切线的情况。

如果我们的直线只与两点相交，那么这意味着它是曲线的切线。很容易看出，和的结果对称于这两点中的一个。

假设 $P$ 是切点。在前一种情况下，我们会写成 $P+P=-Q$。现在这个方程变成了 $P+Q=-P$。另一方面，如果 $Q$ 是切点，正确的方程将是 $P+Q=-Q$。

几何方法现在已经完成，涵盖了所有情况。有了一支铅笔和一把尺，我们能够对任何椭圆曲线上的每个点执行加法。如果你想尝试，请看看我为计算椭圆曲线上的和构建的 HTML5/JavaScript 可视化工具！

代数加法

如果我们希望计算机执行点加法，我们需要将几何方法转化为代数方法。将上述规则转化为一组方程似乎很简单，但实际上可能非常繁琐，因为它需要解决三次方程。因此，在这里我只报告结果。

首先，让我们摆脱最烦人的特殊情况。我们已经知道 $P+ (-P) = 0$，我们也知道 $P+ 0 = 0 + P = P$。因此，在我们的方程中，我们将避免这两种情况，只考虑两个非零、非对称的点 $P = (x_P, y_P)$ 和 $Q = (x_Q, y_Q)$。

如果 $P$ 和 $Q$ 不同（$x_P \neq x_Q $），通过它们的直线的斜率为：

$$ m = \frac{y_P - y_Q}{x_P - x_Q} $$

这条直线与椭圆曲线的交点是第三个点 $R = (x_R, y_R)$：

$$ x_R = m^2 - x_P - x_Q $$ $$ y_R = y_P + m(x_R - x_P) $$

或者，等价地：

$$ y_R = y_Q + m(x_R - x_Q) $$

因此 $ (x_P, y_P) + (x_Q, y_Q) = ( x_R, -y_R) )$（注意符号并记住 $P + Q = -R$）。

如果我们想要检查这个结果是否正确，我们需要检查 $R$ 是否属于曲线，以及 $P$、$Q$ 和 $R$ 是否共线。检查点是否共线很简单，检查 $R$ 是否属于曲线则不是，因为我们需要解决一个三次方程。

相反，让我们用一个例子来说明：根据我们的 可视化工具，给定 $P=(1, 2)$ 和 $Q=(3, 4)$，在曲线 $y^2 = x^3 - 7x + 10$ 上，它们的和为 $P+Q = -R = (-3, 2)$。让我们看看我们的方程是否正确：

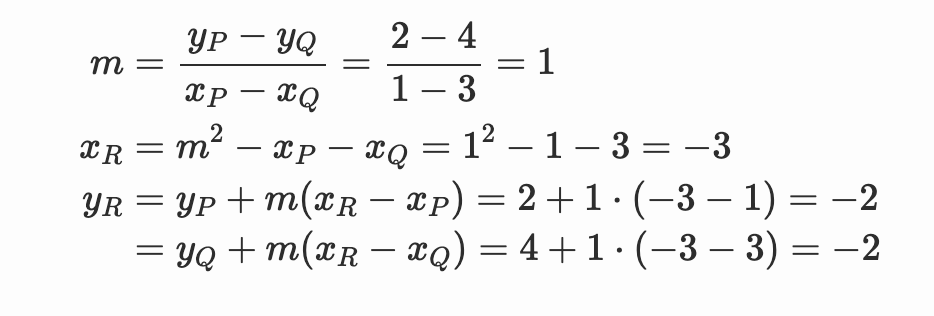
是的，这是正确的！

请注意，即使$P$ 或 $Q$中的一个是切点，这些方程也适用。让我们尝试 $p=(-1, 4)$ 和 $Q=(1,2)$。

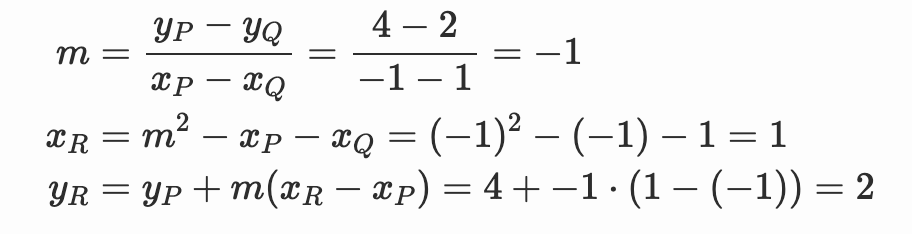
我们得到结果 $P + Q = (1, -2)$，与 可视化工具 给出的结果相同。

$P = Q$ 的情况需要稍微不同对待：$x_R$ 和 $y_R$ 的方程是相同的，但鉴于 $x_P=x_Q$，我们必须使用不同的斜率方程：

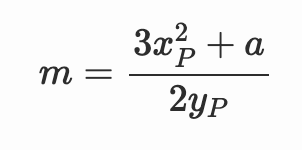
请注意，正如我们所期望的，这个表达式是：

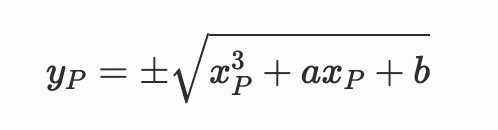
这个结果的有效性可以通过检查 $R$ 是否属于曲线以及通过 $P$ 和 $R$ 的直线是否只与曲线有两个交点来证明。但再次，我们不会证明这一点，而是尝试一个例子：$P=Q=(1, 2)$。

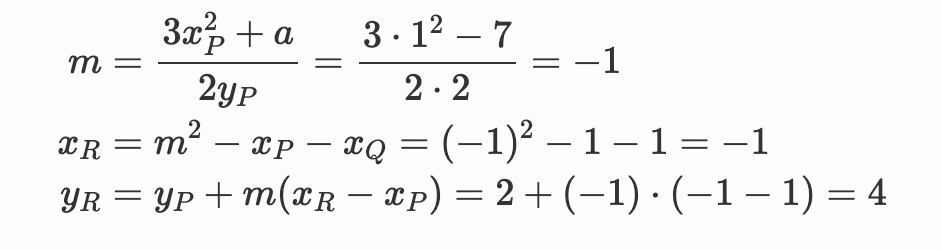
这给出了 $P+P = -R = (-1, -4)$。 正确 ！

尽管推导这些方程的过程可能非常繁琐，但我们的方程非常简洁。这要归功于韦达斯特拉斯正规形式：没有它，这些方程可能会变得非常冗长和复杂！

标量乘法（Scalar multiplication）

除了加法，我们可以定义另一种操作：标量乘法，即：

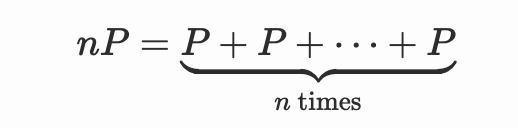
其中 $n$ 是自然数。我还为标量乘法编写了一个可视化工具，如果你想尝试一下。

按照这种形式编写，计算 $nP$ 看起来需要 $n$ 次加法。如果 $n$ 有 $k$ 个二进制位，那么我们的算法将是 $O(2^k)$，这并不是很好。但是存在更快的算法。

其中之一是双倍（double）加法算法。其操作原理可以通过一个例子更好地解释。取 $n=151$。它的二进制表示为 $10010111_2$。这个二进制表示可以转换为二的幂的和：

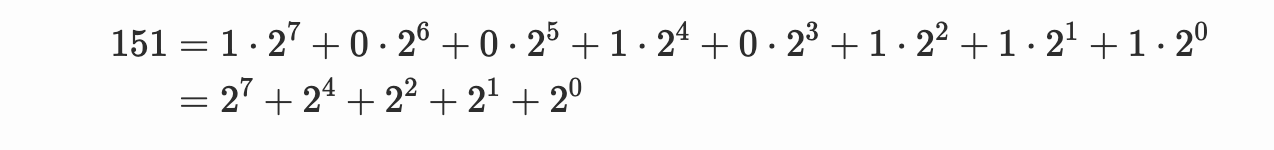
（我们取了每个二进制位并将其乘以二的幂。）

基于此，我们可以写成：

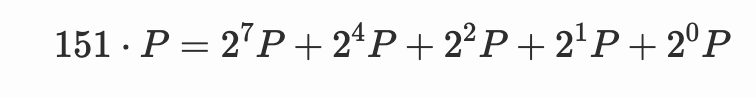
双倍加法算法告诉我们要做的是：

• 取 $P$。
• _双倍_它，这样我们就得到了 $2P$。
• 将 $2P$ 加到 $P$（以获得 $2^1P + 2^0P$ 的结果）。
• 双倍 $2P$，这样我们就得到了 $2^2P$。
• 将其添加到我们的结果（这样我们就得到了 $2^2P + 2^1P + 2^0P$）。
• 双倍 $2^2P$ 以获得 $2^3P$。
• 不要执行任何涉及 $2^3P$ 的加法。
• 双倍 $2^3P$ 以获得 $2^4P$。
• 将其添加到我们的结果（这样我们就得到了 $2^4P + 2^2P + 2^1P + 2^0P$）。
• ...

最终，我们只需进行七次双倍和四次加法即可计算 $151 \cdot P$。

如果这还不够清楚，这里有一个实现该算法的 Python 脚本：

def bits(n):
    """
    生成 n 的二进制位，从最低有效位开始。
    bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1
    """
    while n:
        yield n & 1
        n >>= 1

def double_and_add(n, x):
    """
    使用双倍加算法计算 n * x 的结果。
    """
    result = 0
    addend = x

    for bit in bits(n):
        if bit == 1:
            result += addend
        addend *= 2

    return result

如果加倍和加法都是 $O(1)$ 操作，那么该算法的时间复杂度为 $O(\log n)$（或者如果考虑比特长度，则为 $O(k)$），这相当不错。肯定比最初的 $O(n)$ 算法要好得多！

对数

给定 $n$ 和 $P$，我们现在至少有一个多项式时间算法来计算 $Q=nP$。但是反过来呢？如果我们知道 $Q$ 和 $P$ 并且需要找出 $n$呢？这个问题被称为对数问题。我们称之为“对数”而不是“除法”，以符合其他密码系统（在那里我们有指数运算而不是乘法）。

我不知道对数问题的“简单”算法，但是通过乘法进行实验很容易看到一些模式。例如，取曲线 $y^2 = x^3 - 3x + 1$ 和点 $P=(0,1)$。我们可以立即验证，如果 $n$ 是奇数，则 $nP$ 在左半平面的曲线上；如果 $n$ 是偶数，则 $nP$ 在右半平面的曲线上。如果我们进行更多实验，可能会发现更多模式，最终可以带领我们编写一个有效计算该曲线上对数的算法。

但是对数问题有一个变体：离散对数问题。正如我们将在下一篇文章中看到的那样，如果我们缩小我们椭圆曲线的定义域，标量乘法仍然“简单”，而离散对数问题变得“困难”。这种双重性是椭圆曲线密码学的关键组成部分。

下一篇见

今天就到这里，希望你喜欢这篇文章！下周我们将探讨有限域和离散对数问题，以及一些示例和工具供你使用。如果你对这些内容感兴趣，请继续关注！

阅读系列文章的下一篇 »