具有DDH假设的ZKP
- ChinaDeFi 去中心化金融社区
- 发布于 2022-07-29 10:12
- 阅读 3450
网络安全的唯一方向是零信任模式。阻止敏感信息数据泄露的一种方法不是储存这些秘密,而是用随机的预言机代替它们。
Diffie-Hellman部分
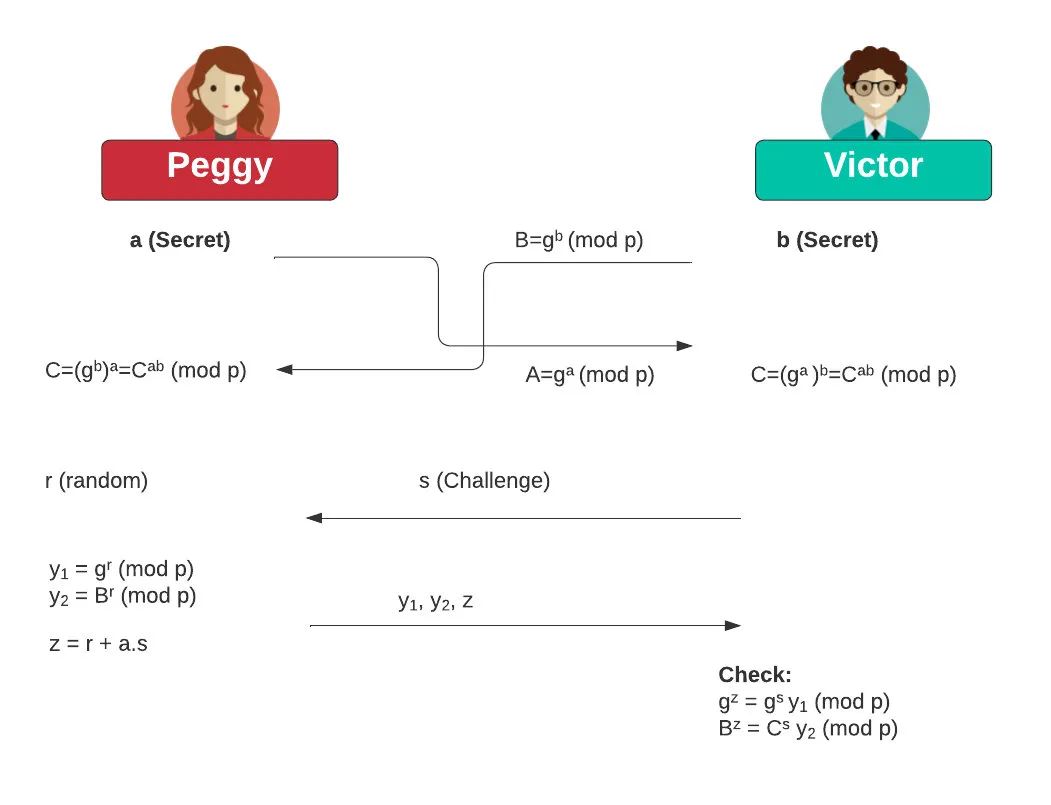
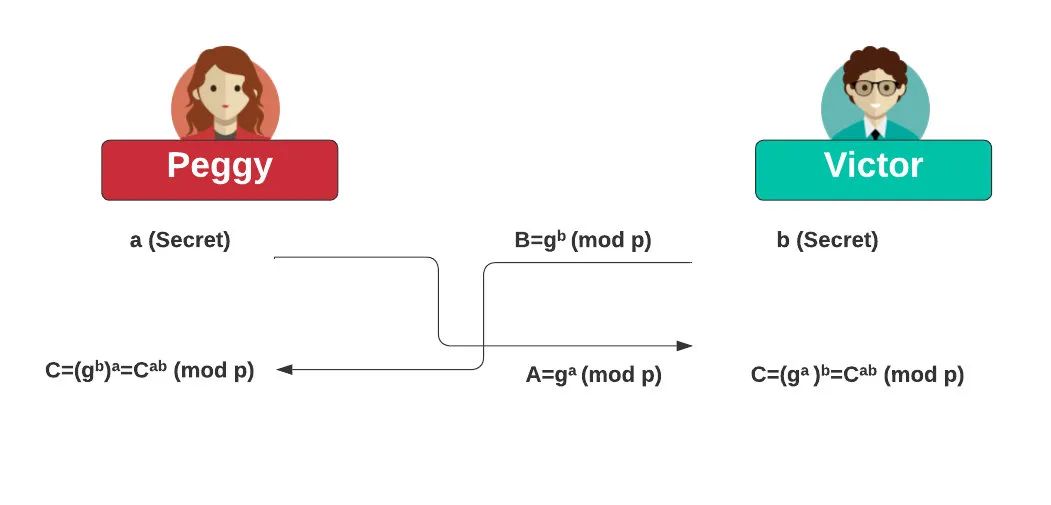
我们必须证明我们仍然持有一个秘密(私有)密钥,这是一个非常典型的情况。那我们怎么把Victor和Peggy绑定到一个证明基础设施中让Peggy向Victor证明她还持有一把私钥呢?为此,我们将通过交换Diffie-Hellman密钥来绑定Victor和Peggy。
在DDH中,我们有一个由 ⟨ g、g^a、g^b、g^{ab }⟩ 组成的元组,其中a和b是秘密。g^a和g^b的值在双方交换后,应该都能生成g^{ab}:
Chaum-Pedersen部分
如果Peggy是证明者,而Victor是验证者,那么Peggy需要表明她知道一个秘密值a。有了Chaum-Pedersen ZKP,Victor让Peggy生成一个ZKP来保护一个秘密。在这个过程中,她将g^a (mod p)的值发送给Victor,当Victor需要证明她仍然知道一个值时,他将发送一个挑战值(s),然后Alice生成一个随机值(r),并返回y_1=g^r和y_2=B^r。然后Victor检查gz=A^s y_1 (mod p)和B^z=C^s y_2 (mod p)是否相等。
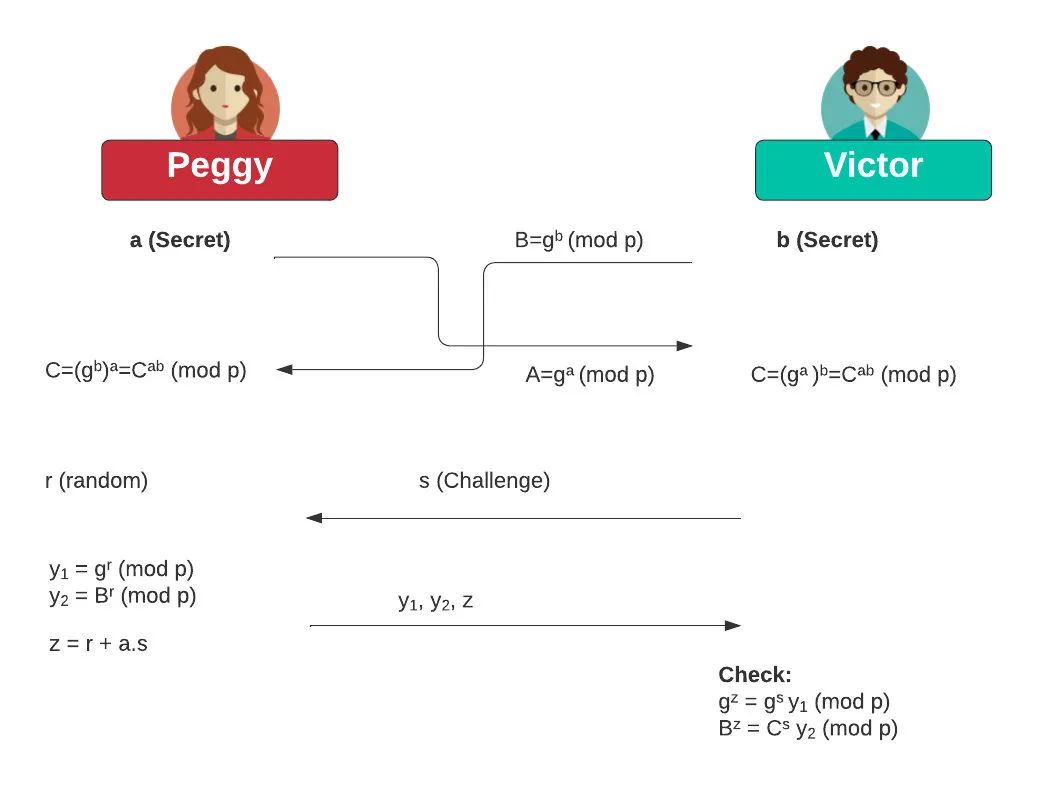
在Victor和Peggy交换他们的秘密后,Victor将持有g^a (mod p), Peggy将持有g^b(mod p)。对于零知识证明,我们这样开始:
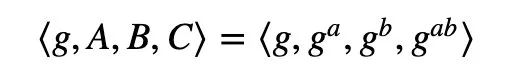
Peggy有一个秘密值a并生成A = g^a。Victor 的秘密值为b并生成B = g^b。他们交换A和B,然后使用 Diffie Hellman 方法生成C。
Victor向Peggy发送一个commitment:
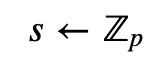
Peggy计算出一个随机值(r):
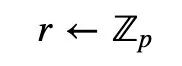
她发给Victor:
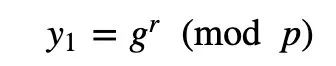
和:
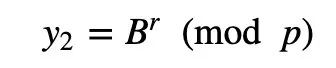
Peggy还发送:
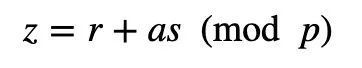
Victor会检查:
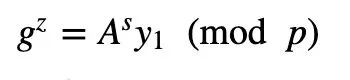
和:
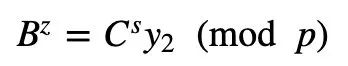
如果这些都是真的,那么Peggy已经证明她知道这个秘密(a)。因为:
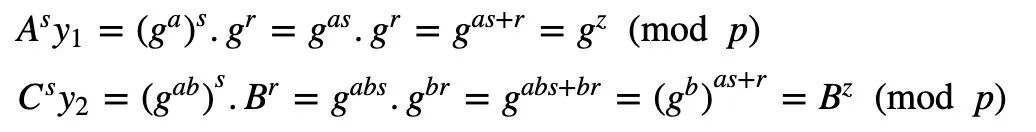
代码
代码如下所示:
import random
import libnum
import sys
bitsize=128
if (len(sys.argv)>1):
bitsize=int(sys.argv[1])
p=libnum.generate_prime(bitsize)
s=random.getrandbits(bitsize)
g=2
a=random.getrandbits(bitsize)
b=random.getrandbits(bitsize)
c=random.getrandbits(bitsize)
r=random.getrandbits(bitsize)
A=pow(g,a,p)
B=pow(g,b,p)
C=pow(g,a*b,p)
y1=pow(g,r,p)
y2=pow(B,r,p)
z=(r+a*s) % (p-1)
print("== Chaum-Pederson ZKP with DDH ==")
print("p=",p)
print("a=",a)
print("A=g^a (mod p)=",A)
print("b=",b)
print("B=g^a (mod p)=",B)
print("ab=",a*b)
print("C=g^{ab} (mod p)=",C)
print("\nProof: g^z = A^s y1")
val1= pow(g,z,p)
val2=(pow(A,s,p)*y1) % p
print("Val1=",val1)
print("Val2=",val2)
if (val1==val2):
print("- Proof verified")
print("\nProof: B^z = C^s y2")
val3= pow(B,z,p)
val4=(pow(C,s,p)*y2) % p
print("Val3=",val3)
print("Val4=",val4)
if (val3==val4):
print("- Proof verified")256位素数的运行示例如下:
== Chaum-Pederson ZKP ==
p= 71808837207067558396943502247178805470599306337269585872075038503116361400603
a= 36623398984913964172485596625205226031763309121917034188846578869320021978402
A=g^a= 32096207796582799691444233880948982714496908564580085529419678203181985482397
b= 31626404664308059618102781249870451013488637545242770934698960204990436278054
B=g^a= 22868249499514124460303251323889043821880224466294750444534923941031732565838
ab= 1158266436479298052448345755868228483694002563526288816181771624565721107667448582344993414115064433575649547672009235534272667805336831732117954454589708
C=g^{ab}= 8021151953795073005899136029637476282156155200732630284950825682466003109726
Proof: g^z = A^s y1
Val1= 9590670516289397297344719778854690756344241363231213529959870845950311348445
Val2= 9590670516289397297344719778854690756344241363231213529959870845950311348445
- Proof verified
Proof: B^z = C^s y2
Val3= 56336209634019548929170814618015392124101293159018455662661735618180853220223
Val4= 56336209634019548929170814618015392124101293159018455662661735618180853220223
- Proof verified结论
网络安全的唯一方向是零信任模式。阻止敏感信息数据泄露的一种方法不是储存这些秘密,而是用随机的预言机代替它们。即便这些预言机被泄漏,真正的秘密也不会被泄漏。在我概述的方法中,我们可以通过散列使用证明的生成值轻松地将其转换为 NI-ZKP(非交互式 ZKP)。
关于
ChinaDeFi - ChinaDeFi.com 是一个研究驱动的DeFi创新组织,同时我们也是区块链开发团队。每天从全球超过500个优质信息源的近900篇内容中,寻找思考更具深度、梳理更为系统的内容,以最快的速度同步到中国市场提供决策辅助材料。
- Zero 链: 技术定位报告 77 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 75 浏览
- 以太坊 2029 Strawmap 傻瓜指南 162 浏览
- 不实的断言:攻破 6 个 zkVMs 94 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 201 浏览
- 零知识编年史:群 158 浏览
- 以太坊执行层优化:状态树与虚拟机 332 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 257 浏览
- 首次 ZK 攻击发生,且出乎意料 268 浏览
- Vitalik: 以太坊量子抵抗路线图 230 浏览
- zkMesh:2026年2月回顾 284 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 291 浏览

