零知识证明 - 从Puzzle理解线性相关
- Star Li
- 发布于 2022-08-16 15:19
- 阅读 4326
zkHack发布了新的Puzzle。虽然Puzzle用的比较老的Groth16算法,Puzzle的内容非常有趣,对理解零知识证明,多项式,线性相关等等知识非常有帮助。
zkHack发布了新的Puzzle。虽然Puzzle用的比较老的Groth16算法,Puzzle的内容非常有趣,对理解零知识证明,多项式,线性相关等等知识非常有帮助。
https://github.com/geometryresearch/zkhack-groth-puzzle
Puzzle基本信息
Puzzle对应的电路采用circom搭建,实现在zkhack-groth-puzzle/circuits/circuit.circom。
pragma circom 2.0.6;
include "../node_modules/circomlib/circuits/poseidon.circom";
template Circuit() {
signal input a;
signal input b;
signal input c;
a === b;
component p = Poseidon(1);
p.inputs[0] <== c;
p.out === 17744324452969507964952966931655538206777558023197549666337974697819074895989;
}电路逻辑非常简单,输入三个变量:a/b/c,其中a是公开输入。逻辑上有两个约束:1/ a和b相等 2/ c的poseidon hash结果是指定的值。使用circom编译成R1CS约束,并采用snarkjs构建相应的证明。Puzzle特别说明了构建证明用了特殊的snarkjs的仓库,有一点改动:
diff --git a/build/main.cjs b/build/main.cjs
index 00e6965..ef1bd6f 100644
--- a/build/main.cjs
+++ b/build/main.cjs
@@ -4328,7 +4328,8 @@ async function newZKey(r1csName, ptauName, zkeyName, logger) {
}
}
- for (let s = 0; s <= nPublic ; s++) {
+// for (let s = 0; s <= nPublic ; s++) {
+ for (let s = 0; s < 1 ; s++) {
const l1t = TAU_G1;
const l1 = sG1*(r1cs.nConstraints + s);
const l2t = BETATAU_G1;就是对证明系统做了这么一点点的改动,就导致最后的证明可变形。
zkhack-groth-puzzle/src/solution.js 给出了Puzzle的要求:
const { proof, publicSignals } = JSON.parse(`{"proof":{"pi_a":["7076778705842675636541778654824835671264842003792815899892788518756808417824","4871300562969249383482829591051792322271432570205055011710223197671646924652","1"],"pi_b": [["4702507968743578934061693422759564470881256571473408115314331474240229998811","16198326042603795115438219508756675682917780977814561672804657276368883889354"],["12916734195569167956837700546311420400354235424337271822709448553494046311159", "20167467333119574021428597666293210644874141810710695584907560968298314755986"],["1","0"]],"pi_c":["20014664648588403789442308373435642542109961553284949305762265534102084844319", "10562544426189233680286850591386198483452124187323754995599976212942563914034","1"],"protocol":"groth16","curve":"bn128"},"publicSignals":["1"]}`);
const isValid = await verifyProof(vKey, { proof, publicSignals });
console.assert(isValid === true, "Proof is not valid");
const new_a = BigInt("PUT_YOUR_ADDRESS_HERE");
publicSignals[0] = new_a;
/*
PUT YOUR SOLUTION HERE
Change the proof such that isValidMalleable = true and passes assertion
*/
const isValidMalleable = await verifyProof(vKey, { proof, publicSignals });
console.assert(isValidMalleable === true, "Malleable is not valid");给定一个证明,如何修改该证明保证在换了公开输入的情况下,验证通过。能换公开输入的Puzzle都比较有趣,我们来看看这次的Puzzle的问题在哪里?
R1CS电路约束
仔细查看Puzzle的电路结构:
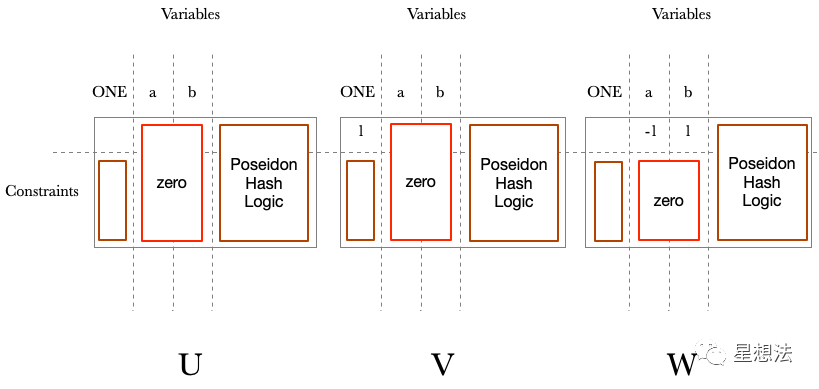


如何解题?
理解了如上的推理过程,确定了线性关系,解题就比较简单了。如果公开输入变量a增大的话,C也做相应的调整:
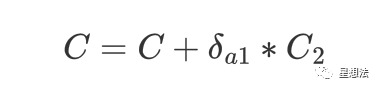
可以查看智能合约的代码,确定验证需要的变量的a的值(zkhack-groth-puzzle/contracts/Puzzle.sol):
uint256 _a = uint256(uint160(address(msg.sender)));
require(
verifyProof(
[_proof[0], _proof[1]],
[[_proof[2], _proof[3]], [_proof[4], _proof[5]]],
[_proof[6], _proof[7]],
[_a]
),
"Puzzle: Invalid proof"
);公开变量a变成了提交交易的地址的后160bits的数据。
如何防止线性关系?
题解完了,需要思考在证明系统中如何避免约束系统部分数据的线性关系。还记得Puzzle本身是对snarkjs进行少量的修改。详细看看这些修改就能得出线性关系防止的方法:
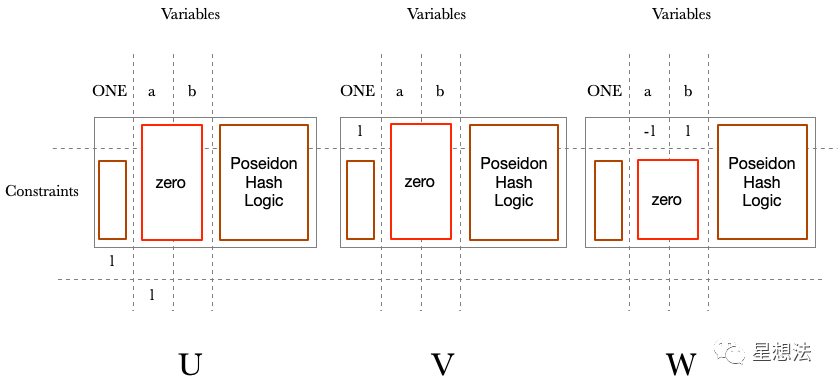
除了约束系统的业务逻辑部分外,针对公开输入部分,扩展约束系统:1*0 = 0。这样的修改即保证了公开输入变量的约束多项式之间是线性非相关的,同时保证了公开输入变量的约束多项式和隐私输入变量的约束多项式是线性非相关。细心的小伙伴可能发现隐私输入变量的约束多项式之间并没有要求线性非相关。
其实,早在2015年类似的问题就在libsnark的代码库被发现,感兴趣的小伙伴可以自行查看。
https://leastauthority.com/blog/a-bug-in-libsnark/
总结:
zkHack新的Puzzle非常有趣,和数据的线性关系有关。在构造的场景下,输入变量的多项式和隐私变量的多项式线性相关。在这样的情况下,可以通过修改已有的证明直接构造其他证明。

- 以太坊 2029 Strawmap 傻瓜指南 36 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 75 浏览
- 零知识编年史:群 50 浏览
- 以太坊执行层优化:状态树与虚拟机 193 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 190 浏览
- 首次 ZK 攻击发生,且出乎意料 213 浏览
- Vitalik: 以太坊量子抵抗路线图 158 浏览
- zkMesh:2026年2月回顾 202 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 183 浏览
- 量子可恢复的 Zcash 185 浏览
- ZK编年史:哈希登场 247 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 445 浏览

