Celestia白皮书中文版(非官方,个人机翻+校正)
- maodaishan
- 发布于 2023-03-29 12:04
- 阅读 4091
Celestia白皮书中文版(非官方,个人机翻+校正)
Abstract
我们提出了 LazyLedger,这是一种分布式账本设计,其中区块链经过优化,仅用于排序和保证交易数据的可用性。执行和验证交易的责任仅转移给对与他们使用的区块链应用程序相关的特定交易感兴趣的客户。由于分布式账本共识系统的核心功能是对交易进行排序并确保其可用性,因此共识参与者不一定需要关心这些交易的内容。这将块验证的问题简化为数据可用性验证,可以以亚线性复杂度的概率实现,而无需下载整个块。因此,达成共识所需的资源量可以最小化,因为交易有效性规则可以与共识规则解耦。我们还实施和评估了几个示例 LazyLedger 应用程序,并验证当使用同一条链的其他应用程序的工作量增加时,特定应用程序的客户端的工作量不会显着增加。
Introdution
到目前为止,基于区块链的分布式账本平台如比特币[1]和以太坊[2]都采用了类似的共识设计范式,其中区块生产者提出的区块的有效性取决于 (i)是否轮到区块生产者提出一个区块和 (ii)根据某个状态机,区块中的交易是否有效。 传统的共识协议,例如 Practical Byzantine Fault Tolerance [3] 也采用了类似的方法,其中共识节点(副本)根据状态机处理事务。困扰去中心化区块链 [4] 的可扩展性问题可归因于这样一个事实,即为了运行验证区块链的节点,节点必须下载、处理和验证链中包含的每笔交易。因此,出现了各种可扩展性工作,包括通过分片进行链上扩展 [5, 6],其目的是将区块链的状态拆分为多个分片,以便不同的共识组可以并行处理事务,并且可以在离线状态下处理事务。通过状态通道进行链扩展 [7, 8],它采用将交易移至链下并使用区块链作为结算层的方法。
但是,也值得探索可能适用于不同类型应用程序的替代区块链设计范例,其中需要验证区块链以确定正确链的节点不需要验证块的内容。相反,在区块链上存储信息的应用程序的最终用户可以关注此类内容的验证。这将消除节点需要验证其他所有人的交易的瓶颈,并将验证区块链的问题减少为简单地验证块的内容是否可用(数据可用性问题 [9]),以便最终用户可以有意义地访问在其应用程序上应用状态转换所需的信息。在这样的范例中,区块链仅用于订购和提供可用消息,而不是执行和验证交易的状态机转换。由于应用程序的消息是由最终用户在链下执行的,这些应用程序的逻辑不需要在链上定义,因此应用程序逻辑可以用任何编程语言或环境编写,更改逻辑不需要硬分叉。将区块链验证减少到数据可用性问题的一个结果是,使用概率数据可用性验证技术 [9],无需下载整个消息集即可完全达成新消息的共识,因为共识参与者不需要处理消息。从哲学上讲,LazyLedger 可以被认为是一个存在于同一条链上的“虚拟”侧链 [10] 系统,因为与每个应用程序相关的交易只需要由这些应用程序的用户处理,类似于以下事实:只有特定侧链的用户需要处理该侧链的交易。但是,由于 LazyLedger 中的所有应用程序共享同一条链,因此其所有交易的数据可用性由同一个共识组平等统一地保证,这与传统侧链不同,其中每个侧链可能具有不同的(较小的)共识组。在本文中,我们做出以下贡献:
- 我们设计了一个区块链 LazyLedger,其中共识和交易有效性是解耦的,并描述了两个替代的块有效性规则,它们只是确保块数据可用。一个是简单的规则,节点只需自己下载块,另一个是概率但更有效,因为节点不需要下载整个块。
- 我们在我们提议的区块链之上构建了一个应用层,最终用户客户端可以有效地查询网络以获取仅与他们的应用程序相关的数据,并且只需要执行与他们的应用程序相关的事务。
- 我们实施并评估了几个示例 LazyLedger 应用程序:包括货币、名称注册商和请愿系统
1. 大纲:
第 2 节介绍了 LazyLedger 所依赖的技术概念的背景;第 3 节介绍了 LazyLedger 威胁模型、节点类型和区块链模型;第 4 节介绍了 LazyLedger 区块链的区块有效性规则;第 5 节介绍了 LazyLedger 应用程序模型以及如何在其区块链之上构建应用程序;第 6 节介绍了对 LazyLedger 原型和一些示例应用程序的评估;第 8 节介绍了与相关工作的比较;第 9 节总结
2 Background
2.1 Blockchains
区块链的数据结构由一个区块链组成。每个块包含两个组件:标题和交易列表。除了其他元数据,头部至少存储前一个块的哈希(从而启用链属性),以及由块中所有交易组成的 Merkle 树的根。区块链网络实现了一种共识算法 [11] 来确定在发生分叉的情况下应该优先选择哪条链,例如,如果使用工作量证明 [1],则优先选择具有最多累积工作量的链。它们还有一组交易有效性规则来规定哪些交易是有效的,因此包含无效交易的区块永远不会受到共识算法的青睐,实际上应该总是被拒绝。全节点(也称为“完全验证节点”)是下载块头和交易列表的节点,根据一些交易有效性规则验证所有交易是否有效。这对于了解共识算法已接受哪些块是必要的。还有一些“轻”客户端只下载块头,并根据交易有效性规则假设交易列表有效。这些节点根据共识规则验证区块,而不是交易有效性规则,因此假设共识是诚实的,因为它们只包括有效的交易。因此,他们不会完全执行共识算法来知道哪些区块被接受,并且最终可能会出现他们接受包含无效交易的,全节点已拒绝的区块的情况。
2.2 Sampling-Based Data Availability
“数据可用性问题”询问客户端(例如轻客户端)如何仅下载块头,而不下载相应的块数据(例如,交易列表),如何满足自己的块数据没有被块的生产者(例如矿工),并且网络确实可以使用完整的数据。巴萨姆等人[9] 提出了一种基于纠删码和随机采样的解决方案。该解决方案是在状态转换欺诈证明的背景下提出的,但是它具有独立的利益。我们在这里总结一下这个方案。纠错码是纠错码 [12],它可以将由 k 份(即,片段)组成的消息转换为更大的 n 份扩展消息,以便原始消息可以被 n 份的任何子集 k 0 恢复.比率 k’/ n(码率)取决于所使用的纠删码及其参数。例如,Reed-Solomon纠删码[13]可以支持k’ = n/ 2 ,这意味着只需要一半纠删码数据即可恢复原始数据。为了让客户端确保区块数据可用,区块头包含对数据纠删码版本的默克尔树根的承诺。为了让对抗性区块生产者扣留区块的任何部分,他们必须扣留区块的 n 个份额中的至少 k’ 个(例如,使用标准的 Reed-Solomon 编码,这将是区块的至少 50%)。然后,客户端可以从块中随机抽取多个共享,如果由于其中一个样本不可用而没有收到对其样本的响应,则它认为整个块不可用,并且不接受该块。如果一个对抗性的区块生产者从 n 个份额中扣留了 k’个,那么客户端很有可能会采样一个不可用的区块并拒绝该区块。然而,由于区块生产者可能错误地计算纠删码或默克尔树,从而导致区块数据不可恢复,因此需要允许客户端从全节点接收“欺诈证明”以提醒他们纠删码不正确,从而导致客户端下载块数据,重新计算纠删码并验证它与 Merkle 根不匹配。为了防止客户需要下载整个区块数据(这会破坏数据可用性证明比自己下载整个数据更有效的目标),使用了二维擦除编码,这将这些欺诈证明限制在特定轴上:只需下载一行或一列即可证明纠删码计算不正确,因此对于具有 n 个份额的块,欺诈证明的大小约为 O( √ n)(没有 Merkle 证明)。然而,这也要求需要数据可用性保证的客户端下载每个行和列中的共享的 Merkle 根作为块头的一部分,而不是整个数据的单个 Merkle 根,因此需要下载的 Merkle 根的数量下载的数量从 1 增加到 2 √ n,因为有 √ n 行和 √ n 列。 重要的是,要使该方案提供任何保证,网络中必须有最少数量的客户端正在制作足够的样本,以迫使块生产者释放超过 k’ 份以满足所有这些样本,就好像少于 k’ 个共享被释放,块数据可能无法从这些共享中恢复。 这是因为客户端 gossip 将样本下载到请求它的“完整”节点,以便他们可以恢复具有足够份额的完整块,类似于对等文件共享网络。
3 Model
3.1 Threat Model and Nodes
我们在 LazyLedger 中考虑以下类型的节点:
- 共识节点。这些是参与共识集的节点,以决定应将哪些块添加到链中。
- 存储节点。这些节点存储了区块链及其块中所有数据的副本。
- 客户端节点。这些实际上是区块链系统的最终用户。他们参与使用区块链的应用程序或用例,并从与其应用程序相关的存储节点接收交易数据或消息。
这些节点都在对等网络中相互连接,例如,所有节点类型可能与任何其他节点类型有一些连接,并且网络的拓扑是非分层的。然而,如果客户节点希望使用它们的服务,它们可能希望确保它们连接到至少一个存储节点。我们假设诚实节点不受日蚀攻击[14],因此至少连接到另一个诚实节点;也就是说,一个节点将遵循第 4 节中描述的协议并中继消息。这意味着网络没有分裂,因此两个诚实节点之间始终存在网络路径。此外,网络中至少有一个诚实的存储节点。我们还假设存在最大网络延迟 δ,因此如果一个诚实节点可以在时间 T 接收来自网络的消息,那么任何其他诚实节点也可以在时间 T 0 ≤ T + δ 这样做。
3.2 Block Model
我们假设一个区块链数据结构至少包含一个基于哈希的区块头链 H = (h0, h1, ...)。 每个区块头 hi 包含消息列表 Mi = (m0 i , m1 i , ...) 的 Merkle 树的根 mRooti,因此给定函数 root(M) 返回消息列表的 Merkle 根 M,然后根(Mi) = mRooti 。 这不是一个普通的 Merkle 树,而是一个有序的 Merkle 树,我们将其称为“命名空间”Merkle 树,我们在 5.2 节中进行了描述。 如果给定布尔函数 blockValid(h) ∈ {true, false},如果块头 hi 是有效的,则blockValid(hi)一定返回true。 如果一个块是有效的,那么它就有可能被包含在区块链中。 我们假设区块链有一些共识规则来决定哪些有效块有共识被包含在区块链中,并解决分叉。 如果给定一些布尔函数 inChain(h, {H0, H1, ...}) ∈ {true, false} ,那么 inChain(hi , {H0, H1, ...}) 必须 返回 true,其中每个 Hj 是不同的区块头链,{H0, H1, ...} 是观察到的不同链的集合(在分叉的情况下可能有多个)。 请注意,仅当且仅当 blockValid(hi) 返回 true 时,在 hi 上计算 inChain 才能返回 true,而不管从哪个分叉中挑选。 除了这个限制,inChain 使用的特定共识规则是任意的,超出了 LazyLedger 的设计范围。 例如,inChain 可以使用具有最长链规则的工作量证明或权益证明 [1, 11]。
3.3 Goals
考虑到这种威胁模型,LazyLedger 有以下目标: 在下文中,“与应用程序相关的消息”是指计算应用程序状态所必需的消息,将在第 5.1.1 节中进行更深入的讨论。
- Availability-only block validity。如果 mRooti 背后的数据对网络可用,blockValid(hi) 的结果应该为真。因此,这意味着共识节点不需要在块中执行消息。
- Application message retrieval partitioning。客户端节点必须能够从存储节点下载与其使用的应用程序相关的所有消息,而无需为其他应用程序下载任何消息。
- Application message retrieval completeness.。当客户端节点从存储节点下载与他们使用的应用程序相关的消息时,他们必须能够验证他们收到的消息是与其应用程序相关的完整消息集,对于特定的块,并且没有遗漏的消息。
- Application state sovereignty。客户端节点必须能够执行与它们用于计算其应用程序状态的应用程序相关的所有消息,而无需执行来自其他应用程序的消息,除非其他特定应用程序被显式声明为依赖项
4 Block Validity Rule Design
LazyLedger 的关键思想是 blockValid(hi) 的结果应该只取决于计算 mRooti 所需的数据是否可用于网络,而不是取决于块中的任何消息是否对应于满足规则的交易一些状态机(第 3.3 节中的目标 1)。这样,我们可以将交易有效性规则与共识规则解耦,因为 inChain 的结果不依赖于块 Mi 中消息的内容,当 blockValid(hi) 被计算时(回忆下,仅当 blockValid(hi) 返回 true 时, inChain(hi) 返回 true:)。我们认为检查重新计算 mRooti 所需数据的可用性是拥有一个有用的功能区块链的最低要求。这是因为,正如我们将在第 5 节中看到的,客户需要知道区块链中发生的交易,以便了解区块链上应用程序的状态,从而做任何有用的事情。如果块背后的数据不可用,客户端将无法计算其应用程序的状态。 我们提供了数据可用性健全性和一致性的定义,改编自[9],用于第 3 节中描述的威胁模型:
- 定义 1(数据可用性健全性)。如果一个诚实节点接受一个可用的块,那么至少一个诚实存储节点拥有完整的块数据,或者将在某个已知的最大延迟 k × δ 内拥有完整的块数据,其中 δ 是最大网络延迟。
- 定义 2(数据可用性协议)。如果一个诚实节点接受一个可用块,那么所有其他诚实节点将在某个已知的最大延迟 k × δ 内接受该块可用,其中 δ 是最大网络延迟。
我们提供了两种可能的有效性规则,具有不同的权衡取舍。 4.1 节描述了一个简单的有效性规则,它以 100% 的概率满足定义 1 和定义 2,对于 O(n) 带宽成本,其中 n 是块的大小,因为节点必须下载整个块数据以确认它是可用的。 4.2 节描述了一个概率有效性规则,它以高但小于 100% 的概率满足定义 1 和定义 2,但带宽成本为 O(√n+log(√n)),因为块的行和列 Merkle 根且仅需要从块中下载静态数量的样本及其对数大小的 Merkle 证明。第 6 节将进一步分析此带宽成本。
4.1 Simplistic Validity Rule
在简单有效性规则中,当且仅当从网络接收到块头 hi 时,blockValid(hi) 返回 true 。节点也能够从网络下载 Mi 并通过检查 root(Mi) = mRooti验证下载的 Mi 的 Merkle 根是 mRooti 。 当 blockValid(hi) 返回 true 时,如果节点没有数据,它应该请求数据。节点必须将 hi 和 Mi 分发给它所连接的节点。因此,该节点应能在δ(即最大网络延迟)内获得并存储Mi。
- 定理 1。简单有效性规则满足定义 1(稳健性)。证明:如果 blockValid(hi) 在诚实节点上返回 true,则该节点会将 Mi 分发给它所连接的节点,其中至少有一个是诚实的,并且还将运行 blockValid(hi) 并分发 Mi ,依此类推.因此,存储节点将在最大网络延迟 δ 内接收 Mi,其中至少存在一个是诚实的
- 定理 2. 简单有效性规则满足定义 2(协议)。证明:如果 blockValid(hi) 在诚实节点上返回 true,则该节点会将 Mi 分发给它所连接的节点,其中至少有一个是诚实的,并且还将运行 blockValid(hi) 并分发 Mi ,依此类推.因此,所有诚实节点将在最大网络延迟 δ 内收到 Mi,因此 blockValid(hi) 将返回 true,导致它们接受 hi 作为可用块。
4.2 Probabilistic Validity Rule
对于概率有效性规则,blockValid(hi) 使用基于随机采样 Al-Bassam 等人描述的块数据 Mi 的纠删码版本的概率数据可用性方案。 [9] 并在第 2.2 节中进行了总结。定义 1 和定义 2 的证明在 [9] 中提供。与 Simplistic Validity Rule 不同的是,该方案在满足这些定义方面是概率性的,但是它更有效,因为只需要下载一部分块数据即可获得数据可用的高概率保证。例如,如果在一个已划分为 4096 份的块中使用 [9] 中描述的 1 4 码率的 2D Reed-Solomon 编码方案,则只需要下载对应于 0.4% 块数据的 15 个样本。节点实现 99% 的保证块数据可用 [9]。进一步分析将在第 6 节中提供。执行 blockValid(hi) 的带宽成本为 O( √ n + log(√ n)) 其中 n 是块的大小,因为每个节点需要下载 2√ n 行和用于块的 2D 纠删码数据的列 Merkle 根,以及固定数量的共享样本及其对应的 Merkle 证明,以将它们验证为块的行或列根之一(大小为对数)。 如第 2 节所述,该方案仅在网络中有足够的最小数量的节点发出足够数量的样本请求以便网络集体采样足够的份额以能够重建块时才有效,因此最大块大小并且每个节点制作的样本数应设置为合理的值,以便满足此条件。 我们注意到这创造了一个有趣的特性:为了(安全地)增加块大小并因此增加网络的吞吐量,可以增加网络中节点的数量。这与比特币 [1] 等传统区块链系统不同,在传统区块链系统中,将更多完整节点部署到网络不会增加网络的链上吞吐量。通过将块验证减少为数据可用性验证,区块链具有更类似于点对点文件共享网络 [15] 的可扩展性属性,其中向网络添加更多节点会增加网络的存储容量。有关某些块大小所需的最小节点的示例参数设置和数量,请参见 [9] 中的表 1。此外,如第 2 节所述,在错误生成纠删码的情况下(希望很少见),欺诈证明的大小约为 O( √ n),或 O( √ n + √ n log (√ n)) 包括 Merkle 证明(例如,对于具有 225 字节份额的 1MB 块,欺诈证明的大小将为 26KB;有关更多数据,请参见 [9])。
5 Application-Layer Design
5.1 Application Model
 回想一下第 3 节,LazyLedger 有客户端节点,它们在与其应用程序相关的块中读取和写入消息,并且块的内容没有有效性规则,因此任何任意消息都可以包含在块中。 LazyLedger 应用程序类似于智能合约,主要区别在于它们由最终用户客户端而不是共识参与者执行。因此,应用程序逻辑完全由该应用程序的客户在链下定义和商定,因此可以用任何编程语言或环境编写。客户端可以提交要记录在区块链上的消息,该消息指定特定应用程序的事务,然后该应用程序的其他客户端将读取和解析该消息,然后可以修改该应用程序状态的副本。应用程序由它们自己的“命名空间”标识,并且可以解析与特定应用程序关联的格式良好的消息以确定它们的应用程序命名空间。我们假设函数 ns(m) 将消息 m 作为输入并返回其命名空间 ID。因此,如果客户端是 ID 为 nid 的应用程序的用户,它有兴趣读取分类帐中的所有消息 m,使得 ns(m) = nid,以确定其应用程序的状态。
由于区块链的共识不需要检查区块链中包含的任何交易的有效性,因此账本可能包含根据某些应用程序的逻辑被认为无效的交易。因此,我们定义了一个 LazyLedger 应用程序应该使用的不返回错误的状态转换函数。具有 ID 为nid 应用程序:
不能返回错误,因为如果恶意参与者在块中包含无效的 tx,那么应用程序的状态最终会永久错误状态。因此,如果 tx 被转换函数的逻辑认为是错误的,它应该简单地将先前的状态 state 作为新状态返回。
使用 ID 为 nid 的应用程序的客户端应在 transitionnid的逻辑或代码上达成一致。例如,如果一个客户端决定对 transitionnid使用不同的逻辑,那么该客户端将对该应用程序达到与其他所有人不同的最终状态,这实际上意味着他们将使用不同的应用程序,但不会影响其他任何人.
有趣的是,这意味着应用程序的用户可以决定更改该应用程序的逻辑,而无需影响其他应用程序的区块链硬分叉。但是,如果逻辑的不变性很重要,应用程序的创建者可能会决定应用程序的命名空间标识符应该是应用程序逻辑的加密哈希。
回想一下第 3 节,LazyLedger 有客户端节点,它们在与其应用程序相关的块中读取和写入消息,并且块的内容没有有效性规则,因此任何任意消息都可以包含在块中。 LazyLedger 应用程序类似于智能合约,主要区别在于它们由最终用户客户端而不是共识参与者执行。因此,应用程序逻辑完全由该应用程序的客户在链下定义和商定,因此可以用任何编程语言或环境编写。客户端可以提交要记录在区块链上的消息,该消息指定特定应用程序的事务,然后该应用程序的其他客户端将读取和解析该消息,然后可以修改该应用程序状态的副本。应用程序由它们自己的“命名空间”标识,并且可以解析与特定应用程序关联的格式良好的消息以确定它们的应用程序命名空间。我们假设函数 ns(m) 将消息 m 作为输入并返回其命名空间 ID。因此,如果客户端是 ID 为 nid 的应用程序的用户,它有兴趣读取分类帐中的所有消息 m,使得 ns(m) = nid,以确定其应用程序的状态。
由于区块链的共识不需要检查区块链中包含的任何交易的有效性,因此账本可能包含根据某些应用程序的逻辑被认为无效的交易。因此,我们定义了一个 LazyLedger 应用程序应该使用的不返回错误的状态转换函数。具有 ID 为nid 应用程序:
不能返回错误,因为如果恶意参与者在块中包含无效的 tx,那么应用程序的状态最终会永久错误状态。因此,如果 tx 被转换函数的逻辑认为是错误的,它应该简单地将先前的状态 state 作为新状态返回。
使用 ID 为 nid 的应用程序的客户端应在 transitionnid的逻辑或代码上达成一致。例如,如果一个客户端决定对 transitionnid使用不同的逻辑,那么该客户端将对该应用程序达到与其他所有人不同的最终状态,这实际上意味着他们将使用不同的应用程序,但不会影响其他任何人.
有趣的是,这意味着应用程序的用户可以决定更改该应用程序的逻辑,而无需影响其他应用程序的区块链硬分叉。但是,如果逻辑的不变性很重要,应用程序的创建者可能会决定应用程序的命名空间标识符应该是应用程序逻辑的加密哈希。
5.1.1 Cross-Application Calls
一些应用程序可能想要调用其他应用程序(即跨合约调用)。我们考虑应用程序可能想要执行此操作的两种情况:作为前置条件或后置条件。我们考虑一个模型,其中所有跨应用程序调用都可以表示为前置条件或后置条件,类似于例如 Chainspace [5] 的事务模型。 回想第 3.3 节,LazyLedger 的目标 4 是应用程序状态主权,这意味着应用程序的用户不应该执行来自其他不相关应用程序的消息。应用程序可以在其逻辑中将其他应用程序指定为依赖项,其中需要了解依赖项应用程序的状态才能计算应用程序的状态。因此,如果 B 是 A 的依赖项,则应用程序 B 被定义为与应用程序 A 的用户“相关”,但是如果 A 不是 B 的依赖项,则 A 与 B 的用户不相关。为了保留国家主权的概念,这意味着第三方应用程序不能强迫其他应用程序依赖于第三方应用程序的状态。 在前置条件的情况下,应用程序可能具有仅当它所依赖的另一个应用程序处于某种状态时才能执行的功能。在这种情况下,为了验证是否满足这些先决条件,应用程序的客户端还必须下载并验证应用程序的依赖应用程序的状态;但是被依赖应用程序的客户端不需要下载依赖它的应用程序的状态。 例如,考虑一个名称注册器应用程序,其中客户只有在不同货币应用程序中向某个地址汇款时才能注册名称。名称注册商应用程序的客户也必须成为货币应用程序的客户,以验证在注册名称时是否有相应的交易将用于支付名称的资金发送到正确的地址。 在后置条件的情况下,应用程序可能希望在事务之后修改另一个应用程序的状态。仅当其状态正在被修改的应用程序已将执行后置条件的应用程序显式设置为后置条件应用程序的依赖应用程序时,后置条件才可能。这是因为为了执行后置条件,后置条件应用程序的客户端必须下载并验证执行后置条件的应用程序的状态,以验证它是否有权执行后置条件.如果允许任何应用程序在任何应用程序中执行后置条件,则意味着客户端将不得不违背自己的意愿下载和验证其他应用程序,从而违反了第 3.3 节中的目标 4(应用程序状态主权)。然而,后置条件可以通过侧链机制(例如联合挂钩 [10])间接执行,但这超出了本文的范围。
5.2 Storage Nodes and Namespaced Merkle Tree
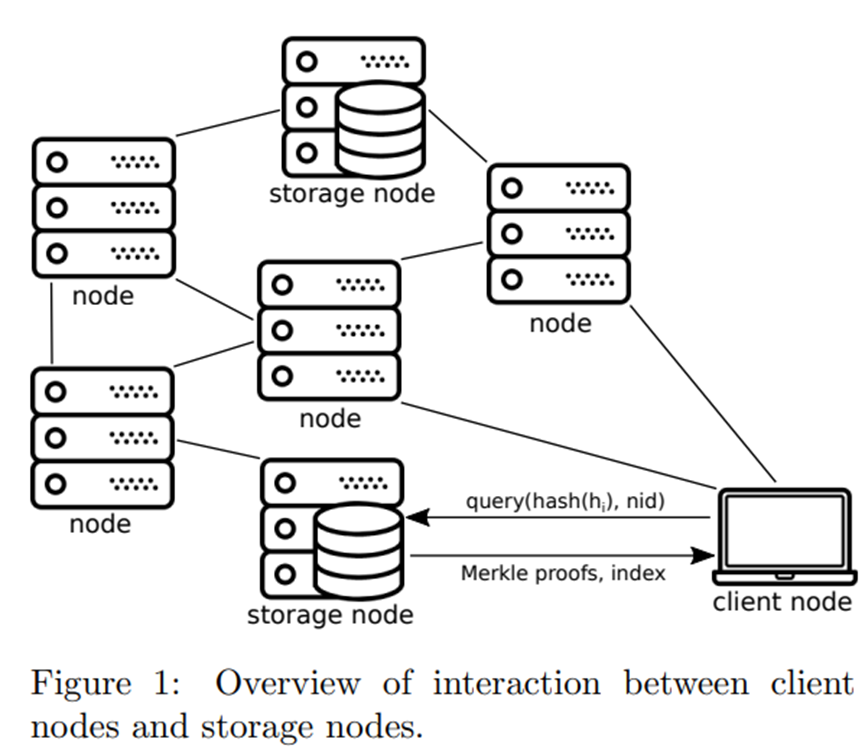
 为了满足第 3.3 节中的目标 2(应用程序消息检索分区),允许客户端节点能够检索与他们感兴趣的应用程序命名空间相关的所有消息,而无需自己下载和解析整个区块链(例如,如果他们使用概率有效性规则,或者简单地假设共识具有诚实多数,只接受可用块),他们可以查询存储节点以获取特定应用程序命名空间中特定块的所有消息。然后,存储节点可以返回 Merkle 证明,以及包含在块中的相关消息。为了允许存储节点向客户端证明他们已经返回了包含在块的 Merkle 消息树中的命名空间的完整消息集(第 3.3 节中的目标 3,应用程序消息检索完整性),我们使用“命名空间”Merkle树如下所述,它是一个有序的 Merkle 树,它使用修改后的哈希函数,使得树中的每个节点都包含每个节点的所有后代中消息的命名空间范围。树中的叶子按消息的名称空间标识符排序。
为了满足第 3.3 节中的目标 2(应用程序消息检索分区),允许客户端节点能够检索与他们感兴趣的应用程序命名空间相关的所有消息,而无需自己下载和解析整个区块链(例如,如果他们使用概率有效性规则,或者简单地假设共识具有诚实多数,只接受可用块),他们可以查询存储节点以获取特定应用程序命名空间中特定块的所有消息。然后,存储节点可以返回 Merkle 证明,以及包含在块中的相关消息。为了允许存储节点向客户端证明他们已经返回了包含在块的 Merkle 消息树中的命名空间的完整消息集(第 3.3 节中的目标 3,应用程序消息检索完整性),我们使用“命名空间”Merkle树如下所述,它是一个有序的 Merkle 树,它使用修改后的哈希函数,使得树中的每个节点都包含每个节点的所有后代中消息的命名空间范围。树中的叶子按消息的名称空间标识符排序。
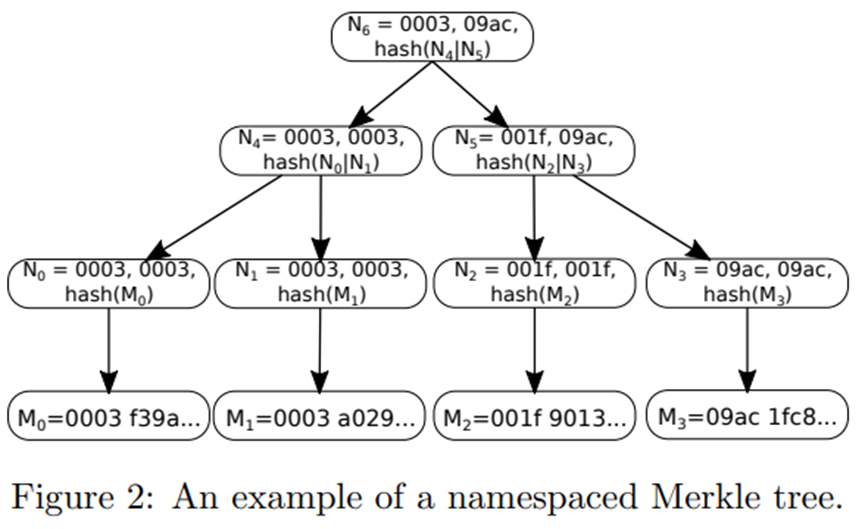
在命名空间默克尔树中,树中的每个非叶节点都包含在作为非叶节点的后代的所有叶节点中找到的最低和最高的命名空间标识符,以及连接的子节点的哈希值。节点。这使得可以创建 Merkle 包含证明,向验证者证明特定命名空间的树的所有元素都已包含在 Merkle 包含证明中。 Merkle 树可以使用标准的未修改的 Merkle 树算法来实现,但是使用依赖于现有哈希函数的修改后的哈希算法,该哈希算法在哈希前面加上名称空间标识符。假设 hash(x) 是一个加密安全的散列函数,例如 SHA-256。我们定义了一个包装函数 nsHash(x),它产生以命名空间标识符为前缀的哈希。命名空间散列的格式为 minNs||maxNs||hash(x),其中 minNs 是在散列表示的节点的所有子节点中找到的最低命名空间标识符,而 maxNs 是最高的。
nsHash(x) 的输出中 minNs 和 maxNs 的值取决于输入 x 是叶子还是两个连接的树节点,如图 2 所示。如果 x 是叶子,则 minNs = maxNs = ns(x) ,因为哈希仅包含一个具有单个命名空间的叶子。
 作恶共识节点可能会尝试生成一个包含 Merkle 树的块,该树的子节点排序不正确。为了防止这种情况,我们可以在 nsHash 中设置一个条件,使得当 leftMaxNs ≥ rightMinNs 时没有有效的哈希,因此对于错误排序的子节点将没有有效的 Merkle 根。因此 blockValid(hi) 将在简单和概率有效性规则中返回 false ,因为在 root(Mi) = mRooti 处不可能有 Mi 。此外,如果树的 Merkle 根构造不正确,例如,如果树中节点的最小和最大命名空间被错误标记,则 root(Mi) = mRooti 和 blockValid(hi) 也会返回 false。因为在 Merkle 树中只修改了哈希函数,所以生成了 Merkle 树,并使用标准算法验证了 Merkle 证明。但是,在 Merkle 证明验证期间,需要额外的步骤来验证证明是否涵盖特定命名空间的所有消息。
作恶共识节点可能会尝试生成一个包含 Merkle 树的块,该树的子节点排序不正确。为了防止这种情况,我们可以在 nsHash 中设置一个条件,使得当 leftMaxNs ≥ rightMinNs 时没有有效的哈希,因此对于错误排序的子节点将没有有效的 Merkle 根。因此 blockValid(hi) 将在简单和概率有效性规则中返回 false ,因为在 root(Mi) = mRooti 处不可能有 Mi 。此外,如果树的 Merkle 根构造不正确,例如,如果树中节点的最小和最大命名空间被错误标记,则 root(Mi) = mRooti 和 blockValid(hi) 也会返回 false。因为在 Merkle 树中只修改了哈希函数,所以生成了 Merkle 树,并使用标准算法验证了 Merkle 证明。但是,在 Merkle 证明验证期间,需要额外的步骤来验证证明是否涵盖特定命名空间的所有消息。
 如果一个块没有与 nid 关联的消息,则只返回一个证明 proof0,它对应于树中左侧的孩子小于 nid 但右侧的孩子大于 nid 的孩子。 child 中的实际消息不需要包含在证明中,因为证明的目的只是表明树中没有 nid 的消息。
如果一个块没有与 nid 关联的消息,则只返回一个证明 proof0,它对应于树中左侧的孩子小于 nid 但右侧的孩子大于 nid 的孩子。 child 中的实际消息不需要包含在证明中,因为证明的目的只是表明树中没有 nid 的消息。
- 定理 3. 假设 Merkle 树是正确构造的,对于 nid 消息的请求,总是可以检测到一组不完整的 Merkle proofs。 proofs = (proof0 , proof1 , ..., proofn)。
证明:让我们假设对手为 nid 返回了一组不完整的正确证明 proofs = (proof0 , proof1 , ..., proofn) ,并且 index 是 proof0 所在的树中的索引。 如果 nid 的省略消息的索引低于索引,则 proof0 将包含一个具有最大命名空间 maxNs 的左兄弟节点,其中 maxNs > nid,从而证明证明集左侧存在省略消息。 如果 nid 的省略消息的索引高于 index+n,则 proofn 将包含具有最小命名空间 minNs 的右兄弟节点,其中 nid > minNs,从而证明证明集右侧存在省略消息。
5.3 DoS-resistance
在 LazyLedger 的设计中,共识节点不负责验证交易,因此作恶客户端可能会为命名空间提交许多无效交易,从而迫使客户端下载许多无效交易。 在许可系统中,共识节点可以选择哪些客户端可以提交交易。 然而,在一个无需许可的系统中,应该有一种方法来确定事务的优先级,并使进行 DoS 攻击变得昂贵。
5.3.1 Transaction Fees
共识节点可以选择优先考虑包含交易费用的交易。但是,理想情况下,任何交易费用系统都不应要求客户端节点去验证那些他们感兴趣的应用程序命名空间中读取消息,也不需要验证实现交易费用支付货币的应用程序。 为了实现这一点,当消息被提交到共识节点,消息的提交者还可以提交“费用交易”,并且还可以将费用支付的“子”消息的哈希附加到费用交易中,这样根据收费逻辑,只有指定哈希背后的消息包含在同一个区块中,才能收取该特殊费用交易中的费用。 支付费用消息的原应用的客户端节点不需要验证收费应用中的费用交易;只有收费应用程序的客户端节点(例如共识节点)才可以。此外,收费系统应用程序的客户端节点不必自己下载子消息来验证它是否已包含在块中并因此获得了费用,而只需验证一个 Merkle 证明,即子消息的哈希值包含在同一块中。为简单起见,我们假设费用交易仅指定一个依赖消息,但它们可能指定多个依赖消息。系统不需要本地货币,因为共识节点可以选择在他们选择认可的任何货币应用程序中接受交易费用。
5.3.2 Maximum Block Size
可以实现最大块大小,而不需要节点下载整个块的数据来验证它是否低于某个大小。 相反,每条消息,以及消息的 Merkle 树中的每个叶子,都可能具有最大大小,这样如果消息 x 大于允许的大小,则 nsHash(x) 将返回错误,因此 root(Mi) = mRooti 因此 blockValid(hi) 将返回 false。 如果需要更大的消息大小,则可以将一条消息分块为多条消息,然后由客户端解析回一条消息。
6 Implementation and Performance
我们用 2,865 行 Golang 代码实现了 LazyLedger 的原型。该代码已作为免费和开源项目发布。 除了核心 LazyLedger 系统,我们还使用 LazyLedger 实现(并发布)了几个示例应用程序。每个应用程序的状态都被实现为一个或多个可以读取或修改的键值存储。应用包括:
- 一种货币应用程序,客户端发布消息,这些消息是用于在椭圆曲线公钥地址之间转移资金的交易。交易由发送者的公钥签名,并指定发送的资金数量和接收地址。在 key-value 存储中,key 是公钥,value 是每个公钥对应的余额,在每次有效交易后更新。
- 一个名称注册应用程序,客户可以: (i) 使用依赖货币应用程序向注册商的公钥发送余额充值交易,以便客户可以使用他们在注册商处的余额支付名称注册费用; (ii) 发送注册交易以将指定名称注册到他们的公钥,这会减少注册人的余额,如果他们的余额足够的话。注册应用程序有一个键值存储,代表每个公钥的应用内充值余额,另一个键值存储,其中每个键代表一个注册名称,每个值代表该名称已注册到的公钥。
- 用于测试目的的虚拟应用程序,它将任意大小的指定键值对添加到其键值存储中。
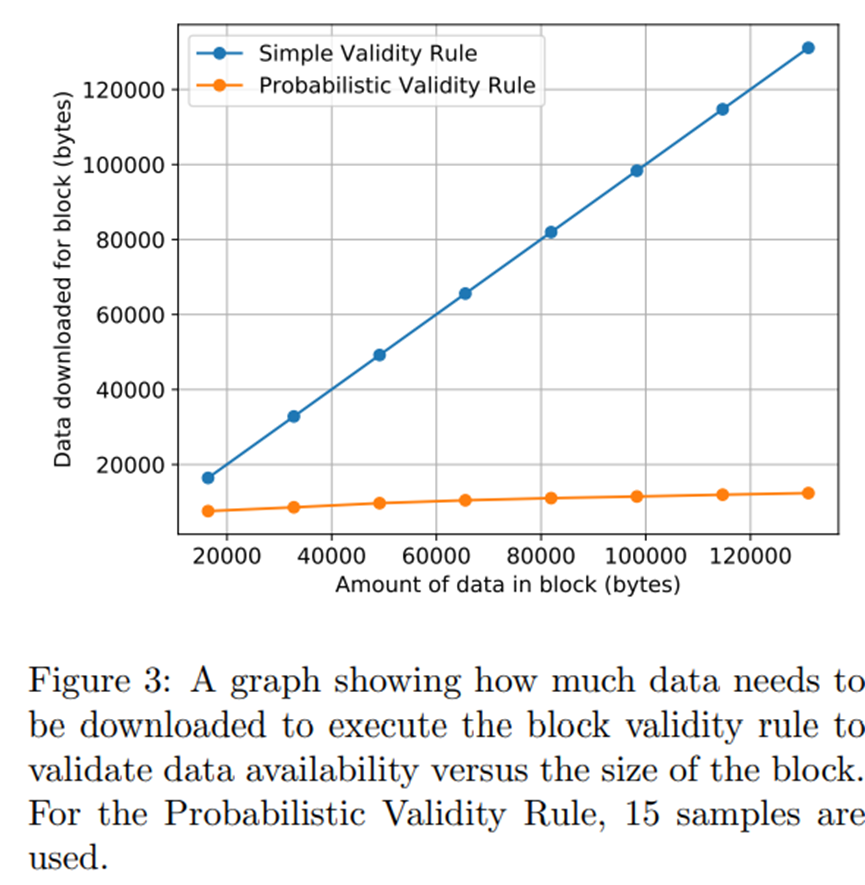 我们对 LazyLedger 的性能和可扩展性属性进行了评估。图 3 比较了需要下载多少数据才能执行简单有效性规则和概率有效性规则以验证数据可用性,适用于不同的块大小。正如预期的那样,块大小和为简单有效性规则下载的数据之间存在线性关系,因为这需要下载所有块数据以确保其可用。然而,我们可以看到,块大小和为概率有效性规则下载的数据之间的关系是亚线性的并且几乎是平坦的。这是因为为了执行概率有效性规则,节点下载固定数量的样本及其相应的 Merkle 证明,其大小随区块大小呈对数增加,以及一组 2√n 行和列 Merkle 根用于块,其中 n 是块的大小。
我们对 LazyLedger 的性能和可扩展性属性进行了评估。图 3 比较了需要下载多少数据才能执行简单有效性规则和概率有效性规则以验证数据可用性,适用于不同的块大小。正如预期的那样,块大小和为简单有效性规则下载的数据之间存在线性关系,因为这需要下载所有块数据以确保其可用。然而,我们可以看到,块大小和为概率有效性规则下载的数据之间的关系是亚线性的并且几乎是平坦的。这是因为为了执行概率有效性规则,节点下载固定数量的样本及其相应的 Merkle 证明,其大小随区块大小呈对数增加,以及一组 2√n 行和列 Merkle 根用于块,其中 n 是块的大小。
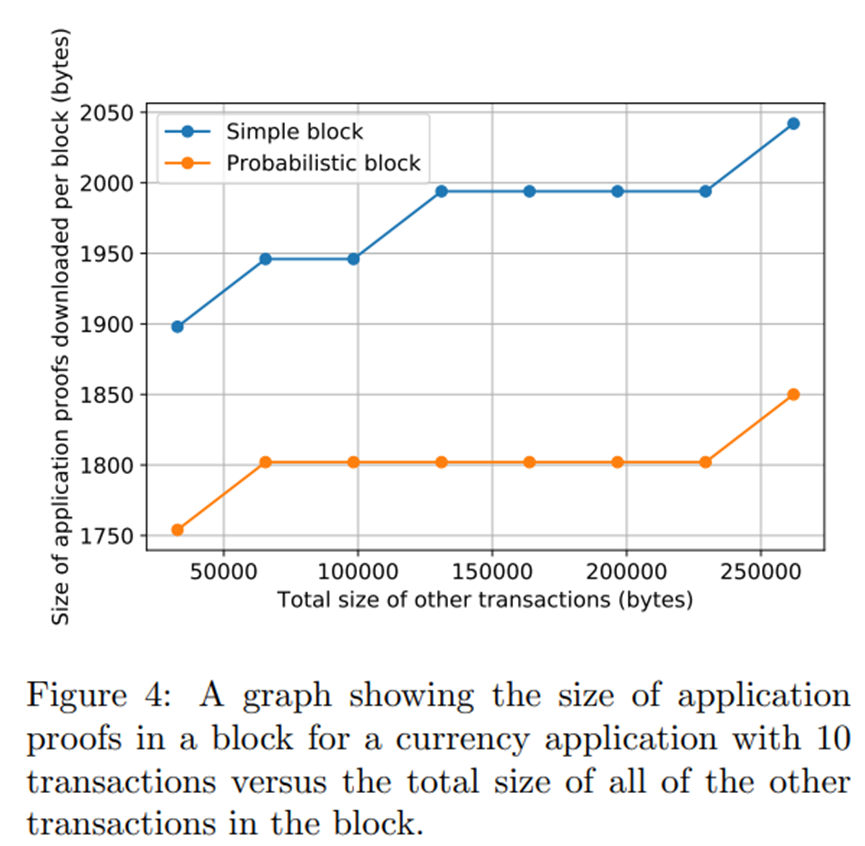 图 4 比较了特定命名空间对存储节点的查询的响应大小(“应用程序证明”),不同命名空间的不同数量的消息(以总字节数衡量)与该查询无关。我们使用货币应用程序消息作为相关的查询命名空间(尽管可以使用任何其他应用程序),将块中的货币消息数固定为 10,但增加了虚拟应用程序消息的总大小。我们可以观察到,对于简单块和概率块,相关应用的应用证明的大小只会以对数方式增加,因为虽然不需要下载不在相关命名空间中的消息,但 Merkle 证明的大小因为这些消息随着块中消息总数的增加而呈对数增加。概率块的应用证明的大小更小,因为使用了二维纠删码,其中每一列和每一行都有自己的默克尔树,因此默克尔证明更小,因为每棵树中的项目较少。
图 4 比较了特定命名空间对存储节点的查询的响应大小(“应用程序证明”),不同命名空间的不同数量的消息(以总字节数衡量)与该查询无关。我们使用货币应用程序消息作为相关的查询命名空间(尽管可以使用任何其他应用程序),将块中的货币消息数固定为 10,但增加了虚拟应用程序消息的总大小。我们可以观察到,对于简单块和概率块,相关应用的应用证明的大小只会以对数方式增加,因为虽然不需要下载不在相关命名空间中的消息,但 Merkle 证明的大小因为这些消息随着块中消息总数的增加而呈对数增加。概率块的应用证明的大小更小,因为使用了二维纠删码,其中每一列和每一行都有自己的默克尔树,因此默克尔证明更小,因为每棵树中的项目较少。
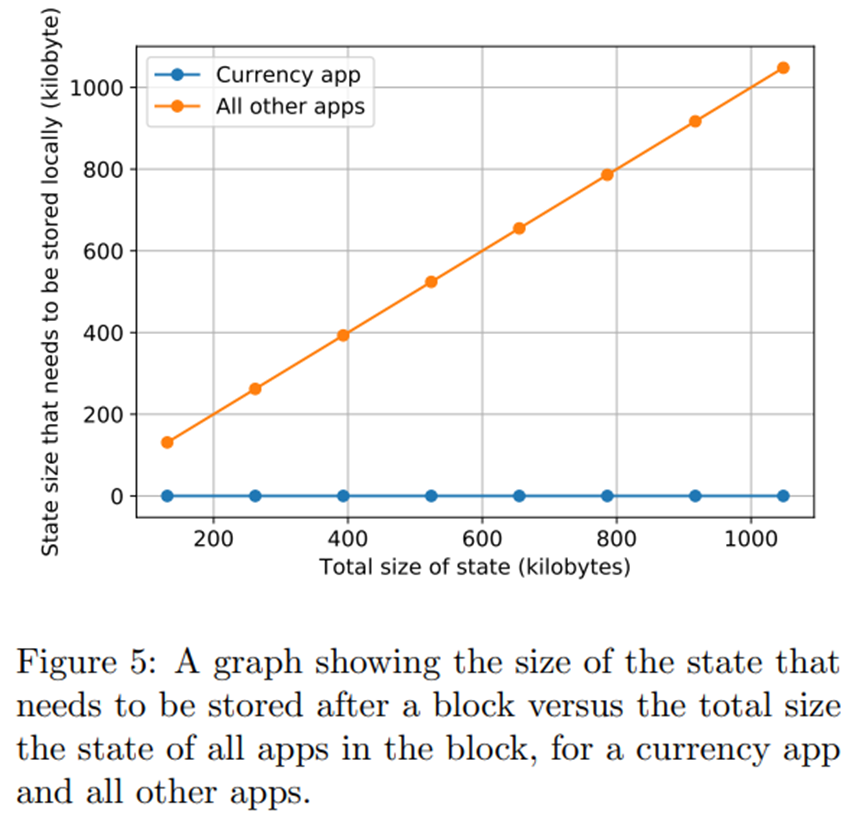 图 5 遵循与图 4 相同的设置,但是我们不是比较货币应用程序的应用程序证明的大小,而是比较相关应用程序的用户需要存储的状态的大小(在这种情况下,货币应用)。正如预期的那样,我们观察到随着其他应用程序状态大小的增加,需要为货币应用程序存储的状态大小保持不变。
图 5 遵循与图 4 相同的设置,但是我们不是比较货币应用程序的应用程序证明的大小,而是比较相关应用程序的用户需要存储的状态的大小(在这种情况下,货币应用)。正如预期的那样,我们观察到随着其他应用程序状态大小的增加,需要为货币应用程序存储的状态大小保持不变。
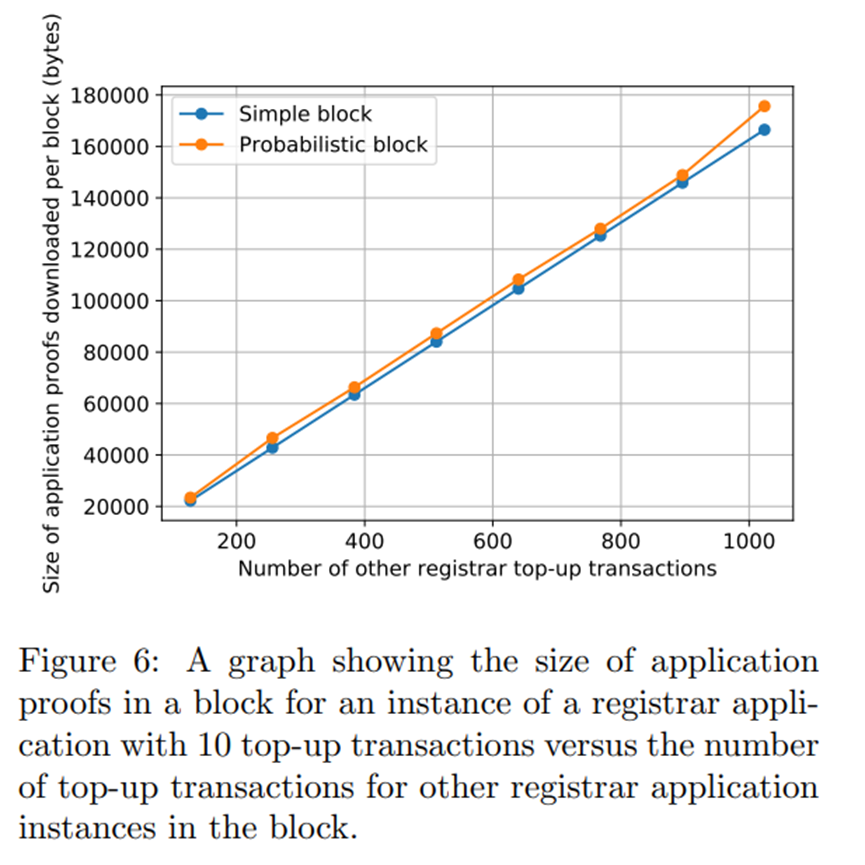
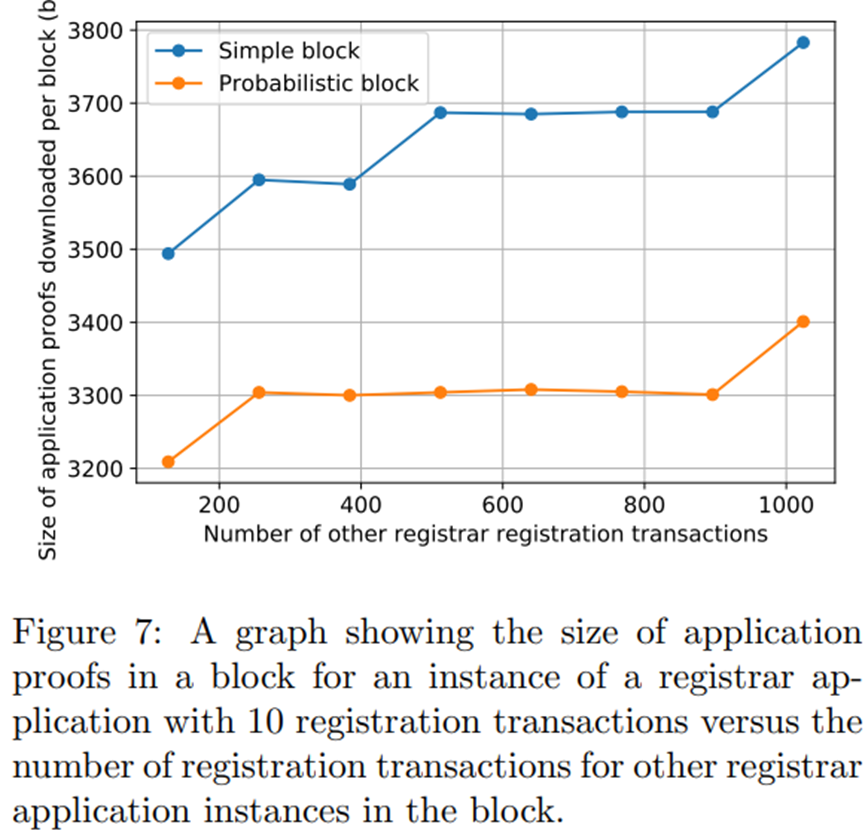 图 6 和图 7 说明了对于具有依赖应用程序的应用程序,应用程序证明的大小可能会如何变化。在这种情况下,我们以名称注册应用程序为例,它要求用户跟踪货币应用程序的状态,以便可以验证到注册商的余额充值交易。在这两个图中,我们为多个注册商设置了多个名称注册应用程序实例,但用户只对关注其中一个感兴趣。在图 6 中我们可以观察到,随着无关名称注册申请的充值交易数量的增加,相关名称注册申请的申请证明的大小线性增加,因为用户还必须下载货币申请的申请证明,其中有其他名称注册应用程序的用户添加到其中的事务。这种只有充值交易的极端情况破坏了 LazyLedger 的任何可扩展性收益,因为所有交易都需要其他用户可能遵循的依赖应用程序中的交易。然而,图 7 显示了相同的情况,但在名称注册交易而不是余额充值交易的情况下。在这里我们看到,无关的名称注册交易不会线性增加需要为其他用户下载的应用证明的大小,因为只有相关名称注册应用程序的用户需要知道已注册的名称,而不会影响依赖应用程序.
图 6 和图 7 说明了对于具有依赖应用程序的应用程序,应用程序证明的大小可能会如何变化。在这种情况下,我们以名称注册应用程序为例,它要求用户跟踪货币应用程序的状态,以便可以验证到注册商的余额充值交易。在这两个图中,我们为多个注册商设置了多个名称注册应用程序实例,但用户只对关注其中一个感兴趣。在图 6 中我们可以观察到,随着无关名称注册申请的充值交易数量的增加,相关名称注册申请的申请证明的大小线性增加,因为用户还必须下载货币申请的申请证明,其中有其他名称注册应用程序的用户添加到其中的事务。这种只有充值交易的极端情况破坏了 LazyLedger 的任何可扩展性收益,因为所有交易都需要其他用户可能遵循的依赖应用程序中的交易。然而,图 7 显示了相同的情况,但在名称注册交易而不是余额充值交易的情况下。在这里我们看到,无关的名称注册交易不会线性增加需要为其他用户下载的应用证明的大小,因为只有相关名称注册应用程序的用户需要知道已注册的名称,而不会影响依赖应用程序.
7 Discussion
Application Light Clients
LazyLedger 当前的限制之一是不清楚如何为应用程序构建轻客户端,因为客户端不必下载应用程序的所有消息来了解应用程序的状态。 这是因为应用程序消息没有被共识节点验证,因此客户端不能假设诚实的大多数已经验证了它们。 这可能是未来工作的一个有趣领域。
Hard Forking
LazyLedger 设计的一个有趣方面是它对区块链治理的影响,特别是硬分叉。传统上,过去曾使用硬分叉来更改交易协议规则 [16] 或扭转因智能合约受到损害而流行的损害,例如 DAO hack [17]。但是对于 LazyLedger,由于没有特定于交易的协议规则,并且块可能包含任意数据,因此无法或不需要硬分叉来更改交易规则或更改系统状态,因为交易的解释留给了设备最终用户的客户而不是共识。因此,如果特定应用程序的用户决定他们想要更改应用程序的状态或“升级”应用程序,他们可以在没有共识或任何链上影响或更改的情况下这样做,只要其他用户实施相同的升级。不实施升级的用户将在本地将应用程序解释为具有不同的状态 - 类似于硬分叉的效果,但不需要明确要求。
8 Related Work
LazyLedger 中命名空间的 Merkle 树的灵感来自 Crosby 和 Wallach [18] 的“标记”Merkle 树概念,其中树中的每个节点都有一个标志,表示其叶子所具有的属性。 Mastercoin(现为 OmniLayer)[19] 是早于以太坊 [2] 的区块链应用系统,它使用比特币有一个协议层来发布消息。这与 LazyLedger 类似,因为区块链可用于发布由客户端解释的任意消息,但是在 Mastercoin 中,所有节点都必须下载所有 Mastercoin 消息,因为比特币基础层不支持有效的数据可用性方案,例如概率有效性规则。此外,由于 Mastercoin 使用比特币作为基础层,它不支持客户端通过特定应用程序查询完整的消息集。最后,Mastercoin 有一套硬编码的应用程序,不支持任意应用程序。相比之下,LazyLedger 研究了理想的新区块链在系统中用作基础层的情况,其中基础层仅用于发布消息和数据可用性。
9 Conclusion
我们提出并评估了 LazyLedger,这是一种独特的区块链设计范式,其中基础层仅用作保证链上消息可用性的机制,交易由最终用户解释和执行。 我们已经表明,通过将块验证减少为数据可用性验证,可以在亚线性时间内验证块。 此外,使用应用程序状态主权的概念,我们已经证明多个主权应用程序可以使用同一条链来实现数据可用性,而对彼此用户的工作量的影响有限。
- 区块链威胁建模 – ImmuneBytes 157 浏览
- Celestia 2.0 愿景:所有市场上链 778 浏览
- 区块链 101:数据处理 1252 浏览
- Layer2战争:为何模块化区块链是2026年Web3的未来 1728 浏览
- 2025年加密货币趋势:更多创新,更混乱的叙事,散户依旧受创 815 浏览
- 051:L3 是什么?它为何成为“Rollup 的 Rollup”? 2718 浏览
- 042:模块化区块链:拆解区块链,重塑性能与自由 2070 浏览
- 所有L1都会迁移到以太坊吗? 2360 浏览
- Celestia 上的私有数据可用性:Hibachi 如何构建隐私优先的永续合约交易所 1518 浏览
- 如何运行由 QuickNode 提供保护的 Celestia 轻节点 1348 浏览
- 即将到来的DEX CLOB战争:链上CLOB的历史与未来 1663 浏览
- Avail 全栈启动:构建一次,随处扩展 536 浏览

