零知识证明 - DIZK介绍

经常有人在提及超大电路证明的时候，谈到DIZK。最近有空，我就看了看DIZK的论文以及源代码。总的来说，从技术人的角度来说，还是有点惊喜，DIZK利用分布式数据处理Apache Spark平台，实现了zk-SNARK证明系统。

DIZK论文是Howard Wu等在2018年发表。论文的下载地址如下：

https://eprint.iacr.org/2018/691.pdf

DIZK，Distributed Zero Knowledge，分布式的零知识证明系统。在分布式环境下，DIZK能支持超大规模电路（10亿门级别）的计算。而且，论文给出的测试数据表明，DIZK的计算性能随着分布式实例的增长，线性增长。

01 DIZK逻辑框架

虽然DIZK是分布式零知识证明系统，零知识证明的协议和计算和传统的证明系统非常像。论文通过两张图给出了两者的区别和联系：

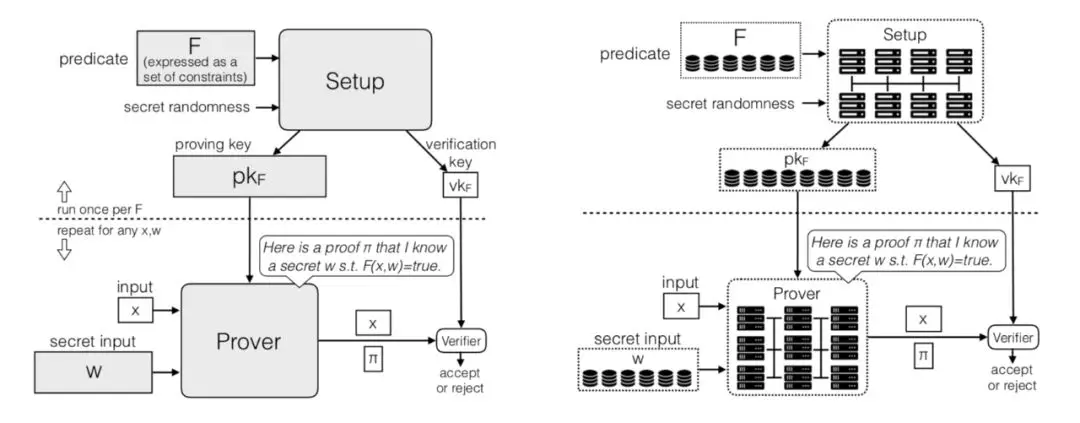
左边代表的是传统的零知识证明（zk-SNARK）系统，主要由三部分计算组成：Setup/Prover/Verifier。右边代表是DIZK的逻辑框架。DIZK将Setup/Prover的计算用分布式实现，计算之间的依赖也用分布式数据表示。Verifier相对来说简单（毫秒级的计算），不需要分布式实现。

02 R1CS/QAP和Groth16

DIZK描述R1CS和QAP的符号体系和其他论文也有点不一样。一个R1CS实例$\phi =(k,N,M,a,b,c)$表示：k代表是输入个数，N是变量个数，M是R1CS的门的个数，a/b/c是一个(1+N)xM的矩阵。每个门由如下的表达式表示：

$(\sum ^N{i=0}a{i,j}zi)\cdot(\sum ^N{i=0}b_{i,j}zi)=\sum ^N{i=0}c_{i,j}z_i$

其中的Zi是所有的输入信息（包括公开输入和隐私输入信息，也就是statement和witness）。

QAP的实例$\Phi =(k,N,M,a,b,c)$表示：k代表是输入个数，N是变量个数，M是R1CS的门的个数，A/B/C是一个长度为1+N的多项式向量，每个多项式的阶小于M。给定输入信息，QAP的实例满足： $(\sum^N_{i=0}A_i(X)zi) \cdot (\sum^N{i=0}B_i(X)zi) = \sum^N{i=0}C_i(X)zi + (\sum^{M-2}{i=0}h_iX^i) \cdot Z_D(X)$

在定义了R1CS和QAP后，DIZK论文给出了Groth16的计算公式（第9页）。

Setup生成Pk/Vk，计算公式如下：

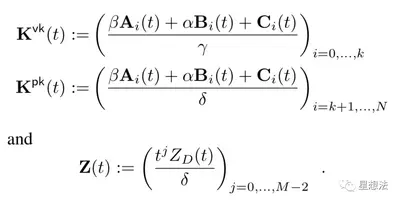
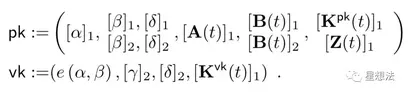
Prover生成证明，计算公式如下：

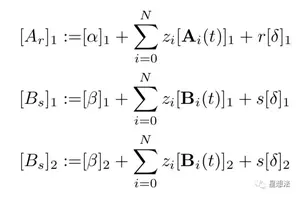
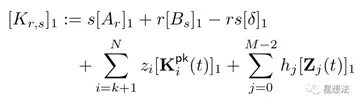
Verifer验证某个证明是否成立，计算公式如下：

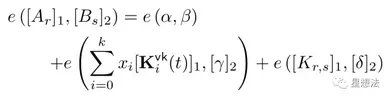
03 Apache Spark

Apache Spark是大数据分布式处理框架。可以查看Spark官方介绍理解Spark的一些逻辑：

http://spark.apache.org/docs/latest/cluster-overview.html

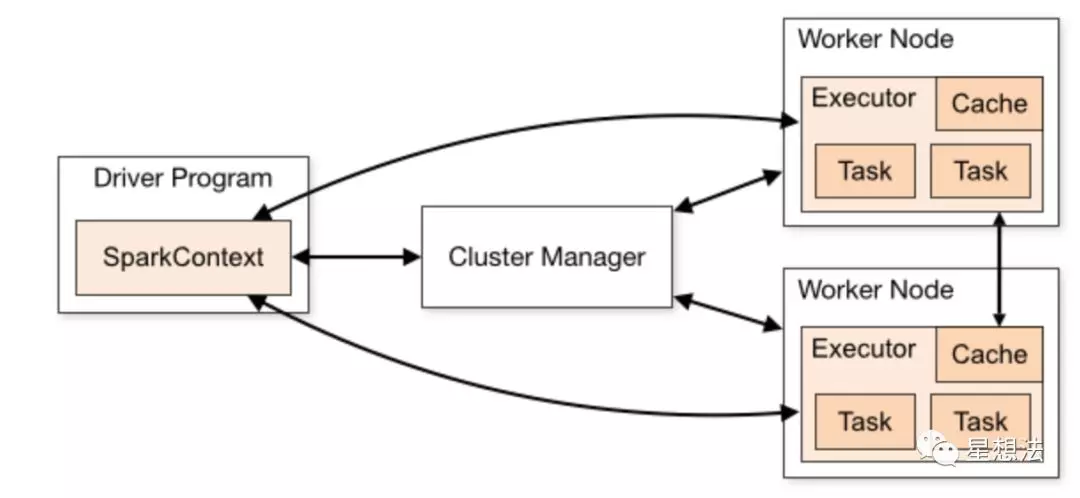
物理上，Spark框架包括三个角色：Driver Program就是Spark框架上编写的程序，Cluster Manager就是集群管理节点，Worker Node就是集群节点。从软件角度看，SparkContext维护了整个程序的执行环境。所有的计算会分解成一个个的Task，所有的Task都由Executor执行。

RDD（Resilient Distributed Datasets）是Spark框架下大数据的表示。你可以理解，RDD是分布式的数据表示。

DIZK设计中，R1CS的电路采用RDD数据表示，因为R1CS电路随着电路门的个数变大而变大。Pk（pubilc key）页是随着门和R1CS的contraint的个数变大而变大，也采用RDD表示。输入信息包括两部分：公开的输入信息和隐私的输入信息。一般来说，公开的输入信息比较小，DIZK直接采用一般向量表示。隐私信息采用RDD数据表示。

04 DIZK计算框架

在Spark的框架上，DIZK设计了Setup和Prover的计算框架：

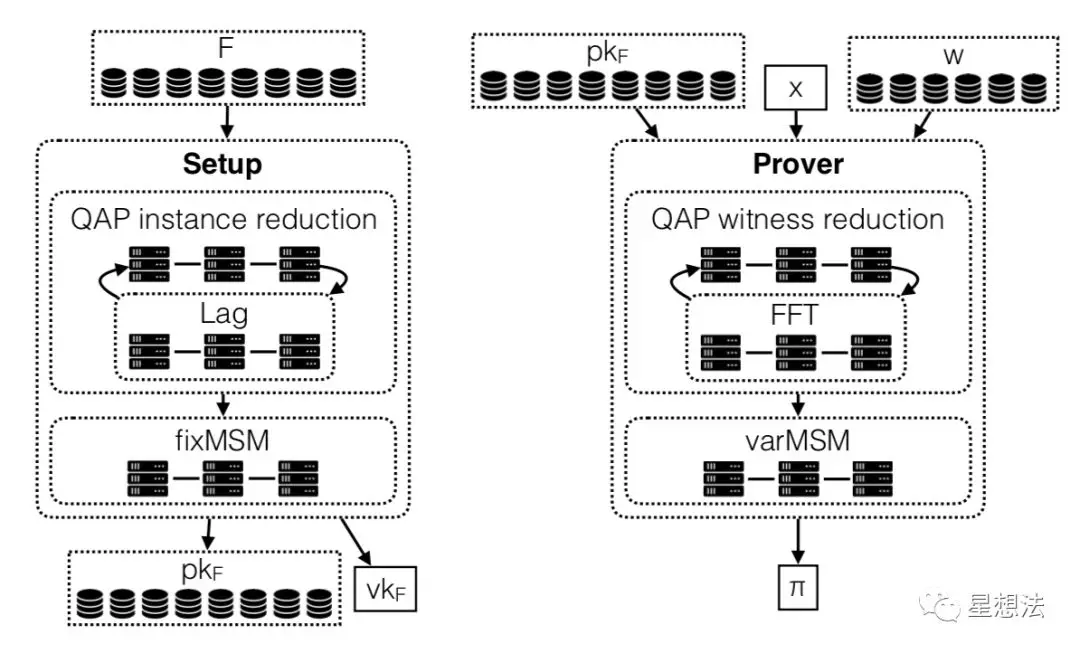
Setup包括两步：1）Lag（拉格朗日插值），R1CS到QAP的转化过程 2）fixMSM - 定点的多倍点加法。Prover也包括两步：1）FFT（计算H多项式）2）varMSM - 不定点的多倍点加法。

DIZK在第4章详细描述了FFT/Lag/fixMSM/varMSM四个计算都能采用分布式算法。简单的说，FFT的分布式算法相对复杂一些，其他三个计算天生可以分布式计算。

分布式计算的核心，是让多个executor执行的计算量尽量均匀。在Lag的计算步骤中，因为R1CS的(1+N)xM的矩阵是稀疏矩阵，DIZK提出了让多个executor均匀计算的方法。

Lag的计算的公式如下：

$(Ai(t))^N{i=0} where Ai(t) := \sum^M{j=1}a_{i,j}L_j(t)$

如果a矩阵是个密集型矩阵的话，只要均匀的切分计算量即可。但是，在现实应用中，a矩阵是个稀疏矩阵。DIZK提出的方法也比较简单明了：预先处理矩阵，统计每列的非零个数。非零个数，代表了计算量。然后再根据这些非零个数，确定计算量的划分。

05 DIZK计算性能

DIZK论文给出了分布式计算的测试结果：

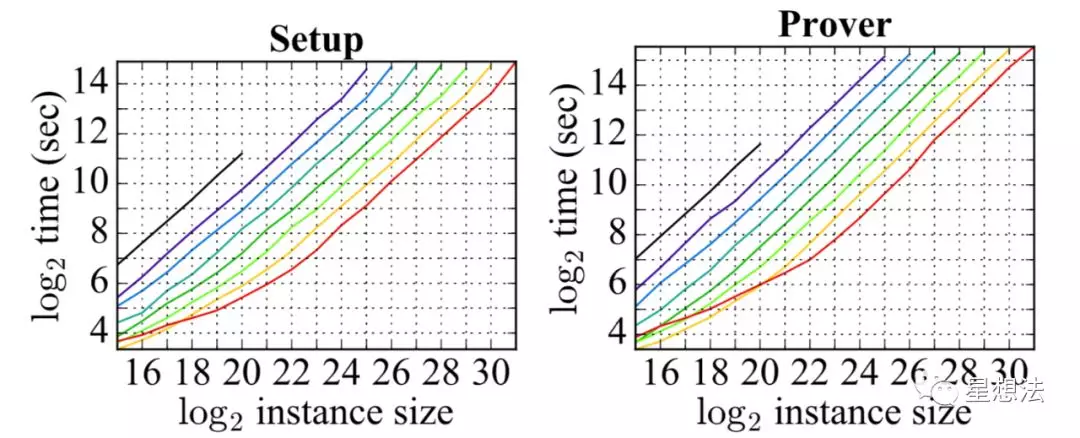
简单的说，DIZK的Setup和Prover计算性能随着计算节点的个数增长成线性增长。

总结：

DIZK，是在Spark大数据计算框架下的分布式零知识证明系统。DIZK详细分析了Groth16的计算，并针对几个计算模块提出了分布式计算算法。从DIZK的测试数据看，DIZK的Setup和Prover计算性能随着计算节点的个数增长成线性增长。

我是Star Li，我的公众号星想法有很多原创高质量文章，欢迎大家扫码关注。