【Plonk SNARK】Plonk IOP协议
- 白菜
- 更新于 2023-08-07 17:50
- 阅读 2012
本系列专题将基于@郭宇老师的视频、讲义及相关论文，系统梳理一下PlonkSNARK的各个组件，尽量做到代码级地剖析深度。预期将涵盖以下几个章节：PlonkIOP协议实现zerokownledge实现Non-Interactivelookup特性Thanks感谢@郭宇老师
本系列专题将基于@郭宇 老师的视频、讲义及相关论文，系统梳理一下Plonk SNARK的各个组件，尽量做到代码级地剖析深度。「如果让我实现一个plonk zkp该如何做」以这样一个角度去看的话，预期将涵盖以下几个章节：
- [Plonk IOP协议]()
- [实现zero kownledge]()
- [实现Non-Interactive]()
- [lookup 特性]()
Thanks
- 感谢@郭宇 老师精彩的视频讲解及教科书级的讲义，通过再次对plonk IOP的学习，对多项式编码、多项式承诺、多项式的线性化、Pairing等有了更深刻的理解，同时对IOP 与 PCS 之间关系有了更清晰的认识
预备知识
-
R1CS 只有乘法gate，也就是说只有乘法才占用一个约束，加法操作不占用约束；与R1CS不同的是，Plonk 电路加法和乘法gate都会占用一个约束 <br />
-
plonk 采用的PCS 方案是kzg10，是一种trust setup 的模式，需要大概了解它与pairing 的勾迹关系 <br />
-
Lagrange 插值法可以把一个scalar 向量以evaluation的形式编码成一个多项式 <br />
-
对composite 连乘多项式或者说非线性化多项式进行commit 是一个困难问题，很难满足每个sub-polynomial 的binding 特性 <br />
-
Vanishing Polynomial 根据Roots of unity 特性很容易算出来，对于Verifier 来说是公开的信息 <br />
-
Quotient Polynomail Prover借助Vanishing Polynomial 也很容易算出来，对于Verifier 来说是未知的信息，需要进行commit
电路算术化
我们要detail的电路结构图如：
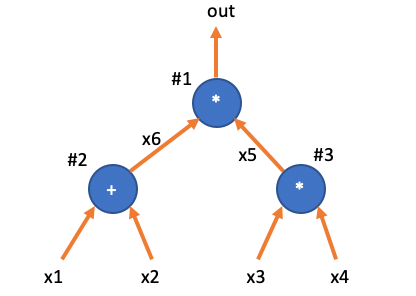<br />
电路gate evaluation 矩阵：
$$ \def\arraystretch{1.5}
\begin{array}{c:c:c:c}
\text{i} & w_a & w_b & w_c \ \hline 0 & \textcolor{red} {x_6} & \textcolor{blue} {x_5} & \textcolor{green} {out} \ \hdashline 1 & x_1 & x_2 & \textcolor{red} {x_6} \ \hdashline 2 & x_3 & x_4 & \textcolor{blue} {x_5} \ \hdashline \end{array} $$
<br />
一个完整的电路描述由三个矩阵来实现。其中，gate 的描述矩阵Q：
$$ \def\arraystretch{1.5}
\begin{array}{c:c:c:c:c}
q_L & q_R & q_M & q_C & q_O \ \hline
0 & 0 & 1 & 0 & 1 \ \hdashline
1 & 1 & 0 & 0 & 1 \ \hdashline
0 & 0 & 1 & 0 & 1 \ \hdashline
\end{array} $$
<br />
gate id的编码矩阵：
$$ \def\arraystretch{1.5}
\begin{array}{c:c:c:c}
i & id_a & id_b & id_c \ \hline
0 & \textcolor{red} {w^0} & \textcolor{blue} {k w^0} & k^2 w^0 \ \hdashline
1 & w^1 & k w^1 & \textcolor{red} {k^2 w^1} \ \hdashline
2 & w^2 & k w^1 & \textcolor{blue} {k^2 w^2} \ \hdashline
\end{array} $$
<br />
wiring 的描述矩阵：
$$ \def\arraystretch{1.5}
\begin{array}{c:c:c:c}
i & \sigma_a & \sigma_b & \sigma_c \ \hline
0 & \textcolor{red} {k^2 w^1} & \textcolor{blue} {k^2 w^2} & k^2 * w^0 \ \hdashline
1 & w^1 & k * w^1 & \textcolor{red} {w^0} \ \hdashline
2 & w^2 & k w^1 & \textcolor{blue} {k w^0} \ \hdashline
\end{array} $$
<br />
多项式编码
鉴于gate 的个数或者constrain 实例的个数为3，多项式编码用的循环乘法子群$H$ 就简化为：
$$ H = (w^0, w^1, w^2) $$ <br />
gate id 矩阵的编码
为了保证wiring 的约束能够顺利进行，gate evaluation 矩阵的三列必须统一编码，为了三列之间不会出现重合的编码，gate id 的编码如下：
$$ \begin{aligned}
id_a &= H = (w^0, w^1, w^2) \
id_b &= k H = (k w^0, k w^1, k w^2) \
id _c &= k^2 H = (k^2 w^0, k^2 w^1, k^2 w^2) \
\end{aligned} $$
<br />
gate evaluation 矩阵的编码
基于gate id 矩阵的三组编码，通过插值的方式，为每列生成相应的多项式：
$$ w_a(X) : H_a \longrightarrow w_a \
w_b(X): H_b \longrightarrow w_b \
w_c(X): H_c \longrightarrow w_c \ $$ <br />
gate 描述矩阵的编码
基于$H$ 通过插值的方式，为每列生成相应的多项式：
$$ q_L(X): H \longrightarrow q_L \
q_R(X): H \longrightarrow q_R \
q_M(X): H \longrightarrow q_M \
q_C(X): H \longrightarrow q_C\
q_O(X): H \longrightarrow q_O \ $$ <br />
wiring 描述矩阵的编码
基于gate id 矩阵的三组编码，通过插值的方式，为每列生成相应的多项式：
$$ \sigma_a(X): H_a \longrightarrow \sigma_a \
\sigma_b(X): H_b \longrightarrow \sigma_b \
\sigma_c(X): H_c \longrightarrow \sigma_c \ $$ <br />
多项式约束
Prover 为了向Verifier 证明它的gate evaluation 矩阵填写的是合法的，需要提供两方面的proof 或者约束。其一，是否满足gate的运算规则；其二，gate的关联或者说wiring 是否合法。 <br />
约束gate的运算规则
$$ q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) \
- q_C(X) - q_O(X) w_c(k^2 X) = 0, X \in H $$ <br />
便于理解，实例化之后展开变成三个约束：
$$ 1 (x_6 x_5) - 1 * out = 0 \
1 x_1 + 1 x_2 - 1 * x_6 = 0 \
1 (x_3 x_4) - 1 * x_5 = 0 \ $$ <br />
约束gate的关联规则
$$ \begin{aligned} \prod_{X \in H}
&\frac{(w_a(X) + \beta id_a(X) + \gamma)} {(w_a(X) + \beta \sigma_a(X) + \gamma)} \
& \frac{(w_b(k X) + \beta id_b(k X) + \gamma)} {(w_b(k X) + \beta \sigma_b(k * X) + \gamma)} \
& \frac{(w_c(k^2 X) + \beta id_c(k^2 X) + \gamma)} {(w_c(k^2 X) + \beta \sigma_c(k^2 * X) + \gamma)} \
&= 1
\end{aligned} $$
<br /> 便于理解，实例化之后展开：
$$ \begin{aligned}
&[ \textcolor{red} {\frac{(x_6 + \beta w^0 + \gamma)}{(x^6 + \beta (k^2 * w^1) + \gamma)}}
-
\textcolor{blue} {\frac{(x_5 + \beta (k w^0) + \gamma)}{(x^5 + \beta (k^2 w^2) + \gamma)}}
-
\frac{(out + \beta (k^2 w^0) + \gamma)}{(out + \beta (k^2 w^0) + \gamma)} ] \
\ & *
[ \frac{(x_1 + \beta w^1 + \gamma)}{(x_1 + \beta w^1 + \gamma)}
-
\frac{(x_2 + \beta (k w^1) + \gamma)}{(x_2 + \beta (k w^1) + \gamma)}
-
\textcolor{red} {\frac{(x_6 + \beta (k^2 w^1) + \gamma)}{(x_6 + \beta * w^0 + \gamma)}} ] \
\ & *
[ \frac{(x_3 + \beta w^2 + \gamma)}{(x_3 + \beta w^2 + \gamma)}
-
\frac{(x_4 + \beta (k w^2) + \gamma)}{(x_4 + \beta (k w^2) + \gamma)}
-
\textcolor{blue} {\frac{(x_5 + \beta (k^2 w^2) + \gamma)}{(x_5 + \beta (k w^0) + \gamma)}} ] \
\ &= 1
\end{aligned} $$
<br /> 简化一下：
$$
\prod_{X \in H}\frac{f(X)}{g(X)} = 1
\textcolor{red} {\Longleftarrow}
\begin{cases} \begin{aligned}
f(X) &= (w_a(X) + \beta * id_a(X) + \gamma) \
& (w_b(X) + \beta id_b(k * X) + \gamma) \
& (w_c(X) + \beta id_c(X) + \gamma), X \in H \
\
g(X) &= (w_a(X) + \beta * \sigma_a(X) + \gamma) \
& (w_b(X) + \beta \sigma_b(k * X) + \gamma) \
& (w_c(X) + \beta \sigma_c(X) + \gamma), X \in H\
\end{aligned} \ \end{cases} $$
<br />
连乘的trace 过程我们用一个中间向量$z_i$ 来表示：
$$ \def\arraystretch{1.5}
\begin{array}{c:c:c:c}
i & X & \frac{f(X)}{g(X)}& z_i \ \hline
0 & w^0 &
\textcolor{red} {\frac{(x_6 + \beta w^0 + \gamma)}{(x^6 + \beta (k^2 * w^1) + \gamma)}}
-
\textcolor{blue} {\frac{(x_5 + \beta (k w^0) + \gamma)}{(x^5 + \beta (k^2 w^2) + \gamma)}}
-
\frac{(out + \beta (k^2 w^0) + \gamma)}{(out + \beta (k^2 w^0) + \gamma)}
& 1 \ \hdashline
1 & w^1 &
\frac{(x_1 + \beta w^1 + \gamma)}{(x_1 + \beta w^1 + \gamma)}
-
\frac{(x_2 + \beta (k w^1) + \gamma)}{(x_2 + \beta (k w^1) + \gamma)}
-
\textcolor{red} {\frac{(x_6 + \beta (k^2 w^1) + \gamma)}{(x_6 + \beta * w^0 + \gamma)}}
& 1 \frac{f(w^0)}{g(w^0)} = \textcolor{red} {\frac{(x_6 + \beta w^0 + \gamma)}{(x^6 + \beta (k^2 w^1) + \gamma)}}
-
\textcolor{blue} {\frac{(x_5 + \beta (k w^0) + \gamma)}{(x^5 + \beta (k^2 w^2) + \gamma)}}
-
\frac{(out + \beta (k^2 w^0) + \gamma)}{(out + \beta (k^2 w^0) + \gamma)} \ \hdashline
2 & w^2 &
\frac{(x_3 + \beta w^2 + \gamma)}{(x_3 + \beta w^2 + \gamma)}
-
\frac{(x_4 + \beta (k w^2) + \gamma)}{(x_4 + \beta (k w^2) + \gamma)}
-
\textcolor{blue} {\frac{(x_5 + \beta (k^2 w^2) + \gamma)}{(x_5 + \beta (k w^0) + \gamma)}}
& 1 \frac{f(w^0)}{g(w^0)} \frac{f(w^1)}{g(w^1)} = \textcolor{blue} {\frac{(x_5 + \beta (k w^0) + \gamma)}{(x^5 + \beta (k^2 w^2) + \gamma)}} \ \hdashline
3 & w^3 = w^0 & - & 1 \frac{f(w^0)}{g(w^0)} \frac{f(w^1)}{g(w^1)} * \frac{f(w^2)}{g(w^2)} = 1
\end{array} $$
<br />
同样，我们通过$H $把向量 $z_i $进行多项式编码，只要满足两条件：
$$ \begin{aligned}
z_0 &= z(w^0) = 1 \textcolor{red} {\Leftrightarrow} L_0(X)(z(X) - 1) = 0 \
z_{i + 1} &= z_i \frac{f_i}{g_i} \textcolor{red} {\Leftrightarrow} z(w X) g(X) - z(X) f(X) = 0 \in H \
\end{aligned} $$
就一定可以推导出$z_3 = 1 \frac{f(w^0)}{g(w^0)} \frac{f(w^1)}{g(w^1)} * \frac{f(w^2)}{g(w^2)} = 1$，也就是说wiring 是合法的。
<br />
fold 所有的约束
gate 运算规则有一条约束，wiring 规则有两条约束，现在通过一个challenge factor 把它们整合起来：
$$ \begin{aligned}
&q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) \ &+ q_C(X) - q_O(X) w_c(k^2 X) \
\
&+ \alpha * (L_0(X)(z(X) - 1)) \
\
&+ \alpha^2 (z(w X) g(X) - z(X) f(X)) \
& = 0, X \in H \
&= t(X) * z_H(X), X \in F \
\end{aligned} $$
<br />
简化一下：
$$ \begin{aligned}
h(X) &= q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) \ &+ q_C(X) - q_O(X) w_c(k^2 X) \
\
&+ \alpha * (L_0(X)(z(X) - 1)) \
\
&+ \alpha^2 (z(w X) g(X) - z(X) f(X)) \
\textcolor{red} {\Downarrow} \ h(X) &= t(X) * z_H(X)， X \in \mathbb{F} \
\end{aligned} $$
所以，整个电路的验证对象就变成上面这一个等式了。 <br />
直觉上的验证过程
最终我们需要验证：
$$ t(X) * z_H(X) = h(X) $$
有多种解决方案：其一，直接通过pairing 的方式来验证：
$$ e([t(X)]_1, [z_H(X)]_2) = e([h(X)]_1, [1]_2) $$
其中$[t(X)]_1$ 和 $[h(X)]_1$ 可以直接拿到，但$z_H(X)_2$不一定，所以还有另外一种方案。
<br />
其二，鉴于Verifier 可以自行计算$z_H(X)$，为了验证上面这个等式成立，最intuitive 的方式是，Verifier 向 Prover 发送一个challenge factor $ξ$或者一个opening，Prover 把$t(X) $和$ h(X)$ 在opening $ξ $上的evaluation 值回传过来。那如何保证两个evaluation 的正确性？需要Prover 分别提供相应的proof，便于Verfier 验证，所以，分两步进行。
<br />
第一步：验证evaluation 的正确性
$$ t(\xi) = K_t \
\Longrightarrow t(X) - K_t = q_t(X)(X - \xi) \
h(\xi) = K_h \
\Longrightarrow h(X) - K_h = q_h(X)(X - \xi) \ $$ <br />
引入challenge factor $ν$ 我们可以把这两个等式fold 在一起：
$$ (t(X) - K_t) + \nu (h(X) - K_h) = (X - \xi) (q_t(X) + \nu * q_h(X)) \
\Updownarrow \
(t(X) + \nu h(X)) - (K_t + \nu K_h) = (X - \xi) (q_t(X) + \nu q_h(X)) $$
<br />
然后再通过pairing 来进行验证，Prover 需要提供$[t(X)]_1、[h(X)]_1、[q_t(X)]_1、[q_h(X)]_1$：
$$ e([(t(X) + \nu h(X)) - (K_t + \nu K_h)]_1, [1]_2) = e([q_t(X) + \nu * q_h(X)]_1, [X - \xi]_2) \
\Updownarrow \
e([t(X)]_1 + v[h(X)]_1 - [K_t + \nu K_h]_1, [1]_2) = e([q_t(X)]_1 + \nu [q_h(X)]_1, [X]_2 - [\xi]_2 ) $$ <br />
第二步：验证目标等式的成立
鉴于Vanishing Polynomial 的evaluation $z_H(\xi)$ Verifier 可以自行解决，在上面两个多项式在同一个opening 上的evaluation验证通过的情况下，Verifier 才能拿着两个多项式的evaluation 值 $K_t、K_h$ 去验证最开始的等式是否成立:
$$ t(\xi) * z_H(\xi) \textcolor{red} {\overset{?} =} h(\xi) \
\Updownarrow \
K_t * z_H(\xi) \textcolor{red} {\overset{?} =} K_h \ $$ <br />
深入验证过程
$$ \boxed{h(X) = t(X) * z_H(X)} \textcolor{red} {\Longleftarrow}
\begin{cases}
\begin{aligned}
f(X) &= (w_a(X) + \beta * id_a(X) + \gamma) \
& (w_b(k X) + \beta id_b(k * X) + \gamma) \
& (w_c(k^2 X) + \beta id_c(k^2 X) + \gamma) \
\
g(X) &= (w_a(X) + \beta * \sigma_a(X) + \gamma) \
& (w_b(k X) + \beta \sigma_b(k * X) + \gamma) \
& (w_c(k^2 X) + \beta \sigma_c(k^2 X) + \gamma) \
\
h(X) &= q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) \
&+ q_C(X) - q_O(X) * w_c(k^2 X) \
&+ \alpha (L_0(X)(z(X) - 1)) \ &+ \alpha^2 (z(w X) g(X) - z(X) f(X)) \
\
z_H(X) &= X^N - 1 \
\end{aligned}
\end{cases} $$
<br />
为了验证左右方框中的等式成立之前，需要验证$h(X)$ 与$t(X)$ 在opening$ ξ$ 上的evaluation $K_h=h(ξ)$ 与$ K_t=t(ξ)$ 是否正确，为此Prover需要提供四个commitment$ [t(X)]_1、[h(X)]_1、[qt(X)]_1、[qh(X)]_1$。我们深入分析一下Prover 是如何一步一步完成的：
验证$t(X)$ 的evaluation
$t(X)$ 首先面临的一个问题是，多项式阶数过高。多项式$f(X)$ 阶数为3N，$z(X)$ 的阶数为N，因此$h(X)$ 的阶数为4N，而$z_H(X)$ 阶数又为N，最后拿到的 $t(X)$ 阶数为3N。如果直接对多项式$t(X)$ 进行commit，必然会加大 SRS 的长度，增大成本。这里我们把多项式$t(X)$ 一分为三，拆分成三个长度为N的多项式，分别用SRS进行commit，SRS的长度不变：
$$ t(X) = t{low}(X) + X^N * t{mid}(X) + X^{2N} * t_{high}(X) $$ <br />
最后Verifier 拿到的是三个多项式的commitment$[t_{low}(X)]1、[t{mid}(X)]1、[t{high}(X)]_1$，整合一下就是:
$$ [t(X)]1 = [t{low}(X)]1 + X^N * [t{mid}(X)]1 + X^{2N} * [t{high}(X)]_1 $$ <br />
如何证明$t(ξ)=K_t$？仍然用pairing的方式来解决：
$$ t(X) - K_t = q_t(X)(X - \xi) \
e([t(X)]_1 - [K_t]_1, [1]2) = e(\pi{t(\tau)}, [X]_2 - [\xi]_2) $$
<br />
完成evaluation 的证明之后，$K_t$ 就可以正式拿来用了。因为Verifier $z_H(ξ)$ 可以自行算出来，所以我们只需要验证:
$$ h(\xi) = K_t * z_H(\xi) $$
<br />
验证$h(X)$ 的evaluation
如何证明$ h(ξ)=K_t∗z_H(ξ)$？可以直接用pairing 的方式来解决吗？
$$ \begin{aligned}
h(X) &= q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) + q_C(X) - q_O(X) * w_c(k^2 X) \
&+ \alpha (L_0(X)(z(X) - 1)) \ &+ \textcolor{red} {\alpha^2 (z(w X) g(X) - z(X) f(X))} \
\end{aligned} $$
不行，因为$h(X)$ 多项式过于复杂，是一种composite 多项式的乘法，对它进行commit是很困难的。可以仔细观察一下式子中每个item，会发现最后一个item 中$z(X)$ 是一个阶数为N的多项式，$f(X)$ 是由三个阶数为N的多项式的连乘。怎么办？我们先把问题简化一下
<br />
简化一下问题，假定有这么一个等式需要证明，三个等式对于Verifier 都是未知的：
$$ a(X) * b(X) = c(X) $$ <br />
最intuitive 的思路是，Verfier 发送challenge factor 或者 opening$ ξ$ 给Prover，Prover 提供三个多项式的evaluation 值$K_a、K_b、K_c$，但如何保证这些evaluation 是正确的，需要额外提供proof，Verfier 拿到这些proof 后先验证evaluation 是否正确，再代入上面的等式去验证：
$$ \begin{aligned}
a(\xi) = K_a &\Longrightarrow a(X) - K_a = q_a(X) * (X - \xi) \
&\Longrightarrow e([a(X)]_1 - [K_a]_1, [1]2) = e(\pi{a(X)}, [X]_2 - [\xi]_2) \
\
b(\xi) = K_b &\Longrightarrow b(X) - K_b = q_b(X) * (X - \xi) \
&\Longrightarrow e([b(X)]_1 - [K_b]_1, [1]2) = e(\pi{b(X)}, [X]_2 - [\xi]_2) \
\
c(\xi) = K_c &\Longrightarrow c(X) - K_c = q_c(X) * (X - \xi) \
&\Longrightarrow e([c(X)]_1 - [K_c]_1, [1]2) = e(\pi{c(X)}, [X]_2 - [\xi]_2) \
\end{aligned} $$
<br />
为了进一步简化问题，我们假定$c(ξ)$ 已知了，只需要 $a(ξ)∗b(ξ)=K_c$ 的正确性，直观上看Prover 分别提供两个多项式的commitment $[a(X)]_1、[b(X)]1$ 和 evaluation的对应的proof $π{a(X)}、π_{b(X)}$，避免误解，这里的两个proof简单展开一下，其实就是两个quotient polynomial 的commitment：
$$ q_a(X) = \frac{a(X) - va}{X - \xi} \Longrightarrow \pi{a(X)} = [q_a(X)]_1 \
q_b(X) = \frac{b(X) - vb}{X - \xi} \Longrightarrow \pi{b(X)} = [q_b(X)]_1 \ $$
<br />
这里一共打开了两个opening，Verifier 需要做两次evaluation的验证，其实只需要打开一次opening就够了。比如只打开$ a(ξ)=K_a$ ，这个evaluation 验证通过之后，接下来需要验证:
$$ K_a * b(X) = K_c \
\Updownarrow \
L(\xi) = K_a * b(\xi) - K_c = 0 $$ <br />
这是一个线性的多项式，直接用pairing 来验证就可以了：
$$ L(X) - 0 = q_L(X) * (X - \xi) \
\Updownarrow \
e([L(X)]_1, [1]2) = e(\pi{L(X)}, [X]_2 - [\xi]_2) \
\Updownarrow \
e(K_a [b(X)]_1 - [K_c]_1, [1]2) = e(\pi{L(X)}, [X]_2 - [\xi]_2) \ $$ <br />
需要Prover 提供$b(X)$的commitment$ [b(X)]1$ 和 evaluation 的proof $π{L(X)}$。到这里，这么一个含composite 多项式等式的验证过程就完成了。关于这里的优化技巧有个专业名词，线性化。
再回到我们的主题:
$$ \begin{aligned}
h(X) &= q_L(X) w_a(X) + q_R(X) w_b(k X) + q_M(X) (w_a(X) w_b(k X)) + q_C(X) - q_O(X) * w_c(k^2 X) \
\
&+ \alpha * (L_0(X)(z(X) - 1)) \
\
&+ \alpha^2 (z(w X) g(X) - z(X) * f(X)) \
\end{aligned} $$ <br />
同样参照多项式线性化的思路，为了验证 $h(ξ)=K_t∗z_H(ξ)$，Verifier 没有必要把$h(X)$ 中的每个多项式都打开，然后对每个多项式的evaluation都验证一遍，其实只需要打开部分多项式，保证打开之后的多项式$h(X)′$ 是一个线性多项式就行：
$$ \begin{aligned}
h(X) &= q_L(X) \textcolor{red} {w_a(X)} + q_R(X) \textcolor{red} {w_b(k X)} \
&+ q_M(X) ( \textcolor{red} {w_a(X)} \textcolor{red} {w_b(k X))} + q_C(X) - q_O(X) * \textcolor{red} {w_c(k^2 X)} \
\
&+ \alpha (L_0(X) (z(X) - 1)) \
\
&+ \alpha^2 (z(w X) (\textcolor{red} {w_a(X)} + \beta * \textcolor{red} {\sigma_a(X)} + \gamma) \
& (\textcolor{red} {w_b(k X)} + \beta \textcolor{red} {\sigma_b(k X)} + \gamma) \
& (\textcolor{red} {w_c(k^2 X)} + \beta \textcolor{red} {\sigma_c(k^2 X)} + \gamma)) \
\
&- \alpha^2 (z(X) (\textcolor{red} {w_a(X)} + \beta * X + \gamma) \
& (\textcolor{red} {w_b(k X)} + \beta k X + \gamma) \
& (\textcolor{red} {w_c(k^2 X)} + \beta k^2 X + \gamma)) \
\end{aligned} $$
<br />
另外，Lagrange basis polynomial $L_0(ξ) $Verifier 可以自己算出来，其中，红色部分的多项式都是需要被打开并验证的，Verifier 打开部分多项式后拿到的$h(X)$ 变成：
$$ \begin{aligned}
h(X)' &= K_{w_a} \textcolor{green} {qL(X)} + K{w_b} \textcolor{green} {qR(X)} + K{w_{ab}} \textcolor{green} {q_M(X)} + \textcolor{green} {qC(X)} - K{w_c} \textcolor{green} {q_O(X)} \
\
&+ \alpha (L_0(\xi) (\textcolor{green} {z(X)} - 1)) \
\
&+ \alpha^2 * (\textcolor{green} {z(w X)} \
& (K_{w_a} + \beta K_{\sigma_a} + \gamma) \
& (K_{w_b} + \beta K_{\sigma_b} + \gamma) \
& (K_{w_c} + \beta K_{\sigma_c} + \gamma)) \
\
&- \alpha^2 * (\textcolor{green} {z(X)} \
& (K_{w_a} + \beta \xi + \gamma) \
& (K_{w_b} + \beta k * \xi + \gamma) \
& (K_{w_c} + \beta k^2 * \xi + \gamma)) \
\end{aligned} $$ <br />
最后除了$ q_L(X)、q_R(X)、q_M(X)、q_C(X)、q_O(X)、z(X)、z(wX)$ 等七个多项式在opening $ξ $上的evaluation 未知，其余的都变成了这些多项式的常量系数，最后Verifier 需要验证：
$$ h(\xi)' = K_t * z_H(\xi) $$
现在左边的多项式已经变成线性的了，所以直接用pairing 的方式来验证：
$$ h(X)' - K_t z_H(\xi) = q_h(X) (X - \xi) \
\Updownarrow \
e([h(X)']_1 - [K_t * z_H(\xi)]_1, [1]2) = e(\pi{h(X)'}, [X]_2 - [\xi]_2) \
$$
其中:
$$ \begin{aligned}
[h(X)']1 &= K{w_a} \textcolor{green} {[q_L(X)]1} + K{w_b} \textcolor{green} {[q_R(X)]1} + K{w_{ab}} \textcolor{green} {[q_M(X)]_1} + \textcolor{green} {qC(X)} - K{w_c} \textcolor{green} {q_O(X)} \
\
&+ \alpha (L_0(\xi) (\textcolor{green} {[z(X)]_1} - 1)) \
\
&+ \alpha^2 * (\textcolor{green} {[z(w X)]_1} \
& (K_{w_a} + \beta K_{\sigma_a} + \gamma) \
& (K_{w_b} + \beta K_{\sigma_b} + \gamma) \
& (K_{w_c} + \beta K_{\sigma_c} + \gamma)) \
\
&- \alpha^2 * (\textcolor{green} {[z(X)]_1} \
& (K_{w_a} + \beta \xi + \gamma) \
& (K_{w_b} + \beta k * \xi + \gamma) \
& (K_{w_c} + \beta k^2 * \xi + \gamma)) \
\end{aligned} $$
所以Prover 只需要提供上面七个还未打开的多项式的commitment $[q_L(X)]_1 、[q_R(X)]_1 、[q_M(X)]_1、[q_C(X)]_1、[q_O(X)]_1、[z(X)]_1、[z(wX)]_1$ 就可以了。到此为止，plonk IOP 协议的整个过程就描述完整了。
<br />
参考资料
-
@郭宇 老师的讲义：https\://github.com/sec-bit/learning-zkp/tree/develop/plonk-intro-cn
-
@郭宇 老师的视频讲解：https\://www.youtube.com/watch?v=O5HGp3EHDI0
