尝试用 Halo2 实现 Tornado Cash

太长不看版：你已经听说过 Tornado Cash 了吗？还有 Halo2？太棒了！在这里，我们将混合这两者，并将 Tornado Cash 电路重写为 Halo2。

太长不看版：你已经听说过 Tornado Cash 了吗？还有 Halo2？太棒了！在这里，我们将混合这两者，并将 Tornado Cash 电路重写为 Halo2。

好的，让我们更好地介绍一下...

“零知识”绝对是一个可怕的词（或者说是两个词）！几个月前，当我开始学习它时，我什么都不懂🤯

最近，我开始学习 Halo2，阅读了一些代码和教程 ，我尝试编写自己的电路，但完全卡住了：我不知道该怎么做...

这就是为什么我决定写这篇文章：学习如何编写电路，并同时教一些其他人。希望你能从中学到一些东西。

本文可能需要更正，或者我说的一些事情可能完全错误。如果是这样：请给我发消息，这样我就可以修复它（同时提高自己的水平😄）。

让我们回顾一下我在开始这个项目时的情况：

  • 阅读了一些 Halo2 教程
  • 我认为我理解了 Chips 和 Circuits 是什么，但我不知道 Layouter 和 Regions 是用来做什么的
  • 我不知道如何编写自己的电路
  • 我绝对不理解事情是如何“在底层”工作的。比如证明是如何从“halo2 board”生成的

这是“第 1 部分”。我们将从尽可能简单的实现开始，接下来的部分将对其进行改进。我还没有写第 2 部分（或第 3 部分，或者更多...），所以如果你在几周/几个月后来到这里，而它们还没有发布，那就意味着我放弃了🥲，所以你可以给我发推特消息告诉我你感到失望。

今天我们的计划如下：

Tornado Cash core

如果你在这里，你可能已经知道 Tornado Cash 是什么。如果不知道 → 什么是 Tornado Cash？

我们将重写“原始”的 Tornado。不是 Tornado Nova。Nova 是一个更新的版本，也非常有趣，但更复杂，所以现在不会研究它。

这是我们将要查看的存储库：Tornado core。

Tornado 有两部分：电路和智能合约。我们只关注电路（尽管我们可能会快速查看合约以便有一个总体了解）。

Tornado 电路是用 Circom 编写的，这就是我们要更改的地方。我们将使用 Halo2，PSE实现（KZG 版本，我会在下一节告诉你更多关于它）来重写这些电路。

好的，谢谢，但是...它是如何工作的？实际上非常简单...

“私密”数字

一切都由称为 secret 和 nullifier 的两个数字保护。就是这样。

这两个数字就是唯一阻止你窃取存放在 tornado 池中的数百万以太币的东西 😱

当你把钱存入 Tornado 时，你需要生成一个随机的 secret 和一个随机的 nullifier。这些数字可以达到 21888242871839275222246405745257275088548364400416034343698204186575808495617（参见这里或这里）。是的，这是一个很大的数字，比 $$ 2^{253} $$ 还要大。

把这些数字写在一个安全的地方，当你想要取回你的钱时，你会需要它们。

Tornado 可以简化为只有两个步骤：

  • 存款 (depositing)
  • 取款 (withdrawing)

让我们更详细地看一下它们。

存款

当你存款时，当然你必须发送 X 以太币（取决于池的情况），但你还必须发送一个 commitment。

这个 commitment 只是前面两个数字的哈希：commitment = H(nullifier, secret)。

Tornado 使用一个 merkle 树来存储这些 commitments。再次抱歉🙏，我不解释 merkle 树是什么。

了解它是如何做的一个很好的方法是看看 Tornado 开发人员编写的前端/cli。这些工具是大多数人用来存款到 Tornado 的（还在使用？）。

这里有 cli 的 deposit() 函数 ，在这里创建了存款

const deposit = createDeposit({
    nullifier: rbigint(31),
    secret: rbigint(31)
});

和 createDeposit()，在这里你可以清楚地看到 commitment 是 nullifier + secret 的哈希

function createDeposit({ nullifier, secret }) {
  const deposit = { nullifier, secret };
  deposit.preimage = Buffer.concat([deposit.nullifier.leInt2Buff(31), deposit.secret.leInt2Buff(31)]);
  deposit.commitment = pedersenHash(deposit.preimage);
  deposit.commitmentHex = toHex(deposit.commitment);
  deposit.nullifierHash = pedersenHash(deposit.nullifier.leInt2Buff(31));
  deposit.nullifierHex = toHex(deposit.nullifierHash);
  return deposit;
}

你可以看到随机数字是如何生成的

const rbigint = (nbytes) => snarkjs.bigInt.leBuff2int(crypto.randomBytes(nbytes));

这些数字是 31 字节长，这意味着最多 $$ 2^{248}$$，比我们之前看到的最大值（ $$ 2^{253} $$ ）要小。所以没问题！

取款

这就变得有趣了。我们如何取回我们的钱呢？

显然，我们将使用 zk 证明：

  • 证明我们知道 secret 和 nullifier，但不会泄露它们
  • 证明我们的 commitment 在 merkle 树中

Nullifier

但 nullifier 到底是用来做什么的？

我们需要一种方法来确保存款只能被取款一次。这就是它的作用。当取款时，nullifier 的哈希被存储在合约中 ，因此 commitment 被“作废”， 不能再次使用 。

为什么我们使用 nullifierHash：因为我们希望确保 nullifier 始终保持私密，所以我们只公开其哈希作为公共值。它同样是唯一的，没有办法逆转它。

让我们看一下 withdraw() 函数 。输入参数有： zk 证明(_proof)和公共输入，包含：树根（_root）、nullifier 哈希(_nullifierHash)、接收地址(_recipient)、中继地址(_relayer)、费用（_fee）和退款（_refund）。

如果我们看一下 Withdraw 电路 ，你同样可以看到这些公共输入。还有私有输入是：

  • secret
  • nullifier
  • merkle 树输入，这些是保持私密的，这样我们就不知道正在取款的是树的哪个叶子

更多细节

哇...这些解释比我想要的要长。至少现在你应该对它是如何工作有一个清晰的认识了。我略去了一些重要的功能，但当我们编写自己的电路时，我们可能会回到它们。

如果你想了解更多细节，请查看以下链接：

通过 Tornado Cash 源代码理解零知识证明

Rareskills - Tornado Cash 的工作原理

为什么选择 Halo2？

Tornado zk 电路是使用 Circom 和 Groth16 证明系统编写的。你可以在 package.json 中查看电路编译脚本，以及在 generateProof 函数中查看。

Groth16 的主要问题之一是它需要基于电路的可信设置。这很烦人，也降低了信任。Plonk的创建，允许进行通用的可信设置。虽然存在一些限制，但基本上：我们只需要做一次，然后每个人都可以基于相同的设置编写电路。

就是这样，让我们把解释保持在最低限度 😊

Halo2 是 Zcash 创建的证明系统，基于 Plonk 并在某种程度上使其更好/更高效（我猜...）。我还不够聪明（但愿😉）来准确理解它为什么如此出色，但一些非常聪明的人告诉我它很好，所以我只是选择相信他们。

所以...今天我们将使用 Halo2 来重建 Tornado Cash。

正如我在开头所说的，实际上我写这篇文章是为了学习 Halo2。我真的不知道它是如何工作的 😂 所以我是边学边写的。

电路设计

正如我们刚才看到的，Tornado 电路实际上非常简单。我们只需要 2 个构建块：

  • 哈希
  • Merkle 树

这些在 Halo2 中被称为“chips”，它们就像类，或者在 circom 中template 类似。在其他Chip或电路中需要时，你可以重复使用它们。

好了...在继续之前，我有一些事情要披露。我将要向你展示的大部分代码，我并没有自己编写。大部分哈希 chip 和 Merkle chip 都是“受到启发”（好吧...大部分是抄袭）自 https://github.com/summa-dev/halo2-experiments

（它本身受到 https://github.com/jtguibas/halo2-merkle-tree 的“启发” 😁）。所以我们要感谢 Enrico、Jin 和 John。

但由于我正在写这篇长篇文章来解释一切，我想这可以弥补一些！

HashChip

这个Chip将两个值进行哈希运算。

在这个第一部分中，我们将使用一个“假”的哈希函数，以使事情变得简单。当我们开始编码时，我会在下一部分给你更多细节。

为了在 Halo2 中正确表示它，我们将需要 3 个 建议列 - Advice（我们的私有值，见证），1 个 instance 列（我们的公共值，生成的哈希）和 1 个 Selector。我们将只使用 1 行。

假设我们想要将单词“hello”和“tornado”进行哈希运算，哈希的结果是“thoerlnlaodo”。

hash chip columns

发生了什么？哈希的结果在证明过程中计算出来（在“Advice 3”中），但它也被证明者作为公共输入传递给了“实例”（显然证明者知道所有的值，所以他可以自己计算哈希）。然后，电路对值应用约束，并确保 advice3 == instance。这就是我们证明我们知道两个初始值（“hello”和“tornado”）的哈希结果是“thoerlnlaodo”的方式。

实际上，在电路中不存在字符串。一切都是数字。

MerkleChip

接下来，我们需要一个Chip来计算/约束我们的 Merkle 树。这个Chip 会复杂一些。

merkle chip columns 我们仍然有 3 个 advice 列，但这次我们需要 2 行。

第一行将取两个节点的哈希。然后交换位将告诉我们节点是否按正确的顺序（左和右）排列，或者需要交换。在下一行，我们有正确顺序的节点，所以我们只需要对它们进行哈希。为了到达树的根，我们只需在循环中执行这个操作，一旦到达根，我们就将其与作为公共输入传递的根进行比较。

电路 (Circuits)

在你将看到一个 HashCircuit 和一个 MerkleCircuit 的代码。这些不是用于我们的 Tornado 电路。它们只是用来测试和更好地理解电路如何工作。

重要的部分是我们的 Tornado 电路。它将作为私有输入接收：

  • nullifier
  • secret
  • path elements
  • path indices

公共输入将是：

  • nullifier hash
  • merkle root

就这样，我认为我们已经准备好进入代码了！

让我们简要总结一下电路中的关系。

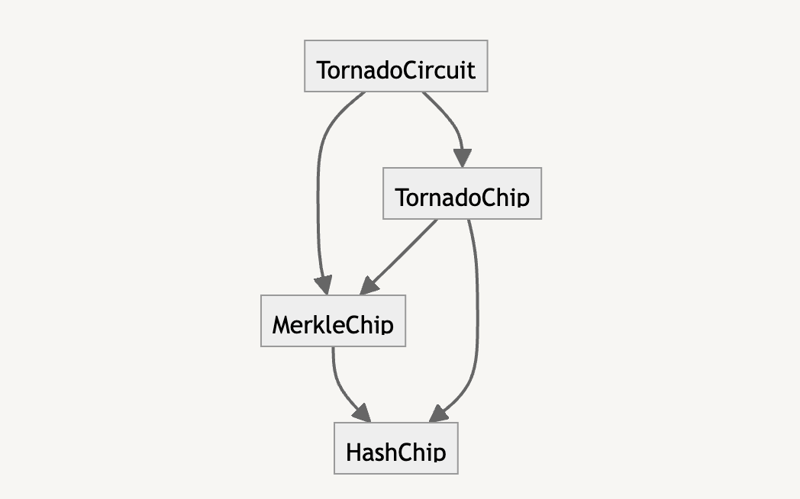
circuit graph

代码

这是最终代码，所以你可以跟着运行它。

哈希

如前面所述，Chip就像一个类。在 halo2_proofs::circuit 中有一个 Chip 特性(trait)，但你不一定非要遵循它，你可以按照你想要的方式编写你的Chip。

电路可以是不同的。为了正确生成你的证明，你将不得不遵循 halo2_proofs::plonk::Circuit 特性(trait)。

我们的Chip 接受一个“config”，这表示你将使用的列的描述（见上表）。

pub struct HashConfig {
    pub advice: [Column<Advice>; 3],
    pub instance: Column<Instance>,
    pub hash_selector: Selector,
}

第一个门

然后我们编写 Chip 和函数 configure()，这是我们定义多项式约束的地方。

我仍然不确定 enable_equality 是用来做什么的，但我认为它使你能够在你的电路中设置复制约束。我看到的每个 halo2 的例子都有这个，所以我只是复制了它。你是对的，这并不聪明... 🤔 提醒我在第二部分文章回来，给出一个更好的解释。

meta.create_gate("hash constraint", |meta| {
    let s = meta.query_selector(hash_selector);
    let a = meta.query_advice(advice[0], Rotation::cur());
    let b = meta.query_advice(advice[1], Rotation::cur());
    let hash_result = meta.query_advice(advice[2], Rotation::cur());
    vec![s * (a * b - hash_result)]
});

为了理解这段代码，首先我得告诉你我是如何作弊的。我没有编写一个真正的哈希函数，我写了一些非常愚蠢的东西。我们的哈希函数接受两个值并将它们相乘以返回一个哈希（记住，每个值都是一个数字）。如果我要用 Python 来写它，它会是这样的：

def hash(a, b):
    return a * b

再次承诺，在第二部分我会改进这个。我们将使用 Poseidon 哈希，一切都会看起来非常漂亮 😎

让我们试着解释一切，这样对于下一个门来说会更容易。

当前我们的门看起来像这样：s * (a * b - hash_result) = 0，可以翻译为：乘以 a 和 b，然后减去 hash_result，如果等于 0，那就没问题。否则 hash_result 是错误的。

s 是我们所谓的“选择器”，它是一个布尔值，将激活或不激活约束。如果它是 0，那么结果就是 0，所以约束通过，我们就不需要确保 a*b = hash_result。如果它是 1，那么 a*b 必须等于 hash_result。

为了获得值 a 和 b，我们使用

let a = meta.query_advice(advice[0], Rotation::cur());

这意味着：获取第一行（Rotation::cur()）或第一个建议列（advice[0]）。这就是在 halo2 中事情总是如何进行的：列和行。如果你想要访问前一行或下一行，你可以使用 Rotation::prev() 或 Rotation::next() 。

Regions and Layouter（区域和布局器）

再次，我将告诉你我是如何理解的。这可能不是最好的表示（但希望不是错误的……），但这是我目前对 Halo2 的理解。对于第二部分文章，我将尝试请一些其他人帮助我更好地将其可视化，并且我会给你另一个视角。

Halo2 将一切都表示为一个大表格（就像 Excel 电子表格）。你可以随心所欲地使用该表格，但它可能会很混乱（这就是为什么我们有Region 区域的原因）。

当生成证明时，每使用一个新列都会增加成本，而行则更便宜。但请记住，你使用的任何新单元格都意味着更多的计算能力。

回到我们的 Excel 比较，如果你想计算 5 个数字的总和，你可以将你的 5 个数字写在 B5 到 B9，然后在 C4 中编写一个“sum()”公式。如果你想在表格的其他地方使用总和结果，比如“F15”，那么你只需引用单元格 C4。

Halo2 也是一样的，你只需为单元格分配值，然后引用它们。为了使事情更有效率，一切都必须划分为Region（区域），这些区域是单元格的块。因此，你定义一个新区域，在这个区域中，你自动可以访问你预先定义的建议/实例列。你填充你的单元格，并知道你添加的约束（在 configure() 中添加的）将会被执行。

你还可以添加新约束，甚至约束区域之间的单元格！哇，这太棒了 😍

Layouter（布局器）只是一个帮助创建区域的工具。在后台，它会优化Region （区域）的创建方式，以便它们不会重叠，并且成本尽可能低。当你想要一个新区域时，你向布局器请求它 layouter.assign_region，然后你可以放心地使用它，而不用担心在表格上搞砸了。

哈希

现在我们来看一下稍微复杂一点的 hash() 函数。

函数签名是

fn hash(
    &self,
    mut layouter: impl Layouter<F>,
    left_cell: AssignedCell<F, F>,
    right_cell: AssignedCell<F, F>,
) -> Result<AssignedCell<F, F>, Error>

left 和 right 可能是值，这会使函数变得更简单。但是作为 AssignedCell 使函数更通用，现在我们可以使用对 board 上的任何单元格的引用。

首先我们分配一个区域:

layouter.assign_region( || "hash row", |mut region| {

然后我们将左单元格的值复制到我们的第一个 Advice 列（第一行）

left_cell.copy_advice(
    || "copy left input",
    &mut region,
    self.config.advice[0],
    0,
)?;

右单元格也是一样，复制到第二个 Advice 列，然后在第三个 Advice 列计算哈希

let hash_result_cell = region.assign_advice(
    || "output",
    self.config.advice[2],
    0,
    || left_cell.value().cloned() * right_cell.value().cloned(),
)?;

最后我们返回计算哈希的单元格的引用。

哈希电路

想象一下，有人公开了一个哈希 H，你想证明你知道 2 个值 a 和 b，当它们一起哈希时会得到 H。但当然你想保持 a 和 b 的私密。

为此，我们看看哈希电路 。

它接受我们的 2 个私有输入 a 和 b

pub struct HashCircuit<F> {
    pub a: Value<F>,
    pub b: Value<F>,
}

我们的公共输入是我们的哈希 H = a * b

let public_inputs = vec![Fp::from(a * b)];

在电路中，最有趣的部分发生在 synthesize 函数中。由于我们的 hash 函数以单元格作为输入，我们将创建一个临时区域，它将保存我们的 a 和 b 值，然后将单元格传递给要进行哈希的函数。

let (left, right) = layouter.assign_region(
    || "private inputs",
    |mut region| {
        let left = region.assign_advice(
            || "private input left",
            config.advice[0],
            0,
            || self.a,
        )?;

        let right = region.assign_advice(
            || "private input right",
            config.advice[1],
            0,
            || self.b,
        )?;

        Ok((left, right))
    },
)?;

let chip = HashChip::construct(config);
let hash_result_cell = chip.hash(layouter.namespace(|| "hasher"), left, right)?;

最重要的部分是最后一行

layouter.constrain_instance(hash_result_cell.cell(), config.instance, 0)

这是我们设置约束的地方。instance 是我们的公共输入所在的列。在这里，我们确保在 hash_result_cell 中得到的哈希与我们公开显示的哈希 H 相等。

默克尔

现在让我们进入 MerkleChip。这应该会更快，因为我们已经理解了所有的基础知识。

当我们将值传递给我们的 hash 函数时，传递 a 和 b 的顺序很重要 H(a,b) != H(b,a)。现在我们当前的哈希函数非常简单，所以值 a 和 b 的顺序并不重要（我们只是将它们相乘）。但当我们“升级”并开始使用 Poseidon 时，顺序就会很重要。

对于我们的默克尔树，我们将注意节点的顺序（左/右）。这就是为什么我们需要一个 swap_bit：节点是否按正确的顺序排列，或者在进行哈希之前它们需要交换？我们还需要 2 个选择器与之配合：

  • swap_selector：检查交换位 → 交换或不交换
  • swap_bit_bool_selector：交换位应该是一个布尔值，所以这检查交换位是 0 还是 1

门

我们的第一个门检查交换位是 0 还是 1。这可以重写为

def is_zero_or_one(value):
    return value * (1 - value) == 0

第二个门更复杂，但并不是那么复杂 😊 我会留给你去尝试理解它。只是为了确保清楚：

left[0] 表示左列，第 0 行

left[1] 表示左列，第 1 行

这就是我们正在检查的

if swap_bit == 1:
    return left[0] == right[1] and right[0] == left[1]
else:
    return left[0] == left[1] and right[0] == right[1]

这就是实际的约束

let constraint1 = (right[0] - left[0]) * swap_bit + left[0] - left[1];
let constraint2 = (left[0] - right[0]) * swap_bit + right[0] - right[1];

计算默克尔树

现在我们的门已经就位，我们需要计算默克尔树根。在 merkle_prove_layer 中：

  • 我们在第 0 行分配左右节点
  • 我们检查交换位
  • 在第 1 行，我们按正确的顺序分配左右节点
  • 我们对节点进行哈希
  • 我们返回哈希结果的单元格

在 prove_tree_root 中，我们只需循环遍历每一层，直到达到根。

同样，在 MerkleCircuit 中，你可以看到它的运行情况。

最重要的部分是

layouter.constrain_instance(root_cell.cell(), config.instance, 1)?;

这是我们验证电路中计算的根是否等于我们作为公共输入传递的根的地方。

Tornado电路

最后！我们来到我们的Tornado电路 。这里是私有输入

pub struct TornadoCircuit<F> {
    nullifier: Value<F>,
    secret: Value<F>,
    path_elements: Vec<Value<F>>,
    path_indices: Vec<Value<F>>,
}

和公共输入

let public_input = vec![nullifier_hash, root];

我们并没有完全遵循真正的Tornado电路 ，它作为公共输入的有：

  • 接收者（recipient）
  • 中继器（relayer）
  • 费用 （fee）
  • 退款 （refund）

这些值在 zk 证明中肯定很重要，并且在验证证明时应该进行检查，但对于我们当前对 Halo2 的理解来说是无用的。所以不会费心使用它们。

以下是电路中采取的步骤：

  • 计算nullifier哈希
  • 检查它是否与公共nullifier哈希匹配
  • 计算 Merkle 树根
  • 检查它是否与公共 Merkle 根匹配

就是这样。非常简单。

范围检查（没做）

我没在 TornadoChip 中设置任何门，这是一个错误，因为我们的电路将是“不完全约束”的。

我们绝对应该对我们的私有输入进行范围检查。范围检查意味着检查一个值是否在某个范围内，即在下限和上限之间。但是，再次强调，让我们把这个留到“第二部分”。

这是原始 Tornado 电路中的范围检查 ：检查 nullifier 和 secret 是否小于 248 位，也就是小于 $$ 2^{248} $$。

nullifier哈希和承诺

在 TornadoChip 中，你会找到一个辅助 compute_hash 函数。这使得nullifier哈希和承诺更容易计算。

这次一切都应该很容易理解，所以我不打算给出太多解释。

只是对最重要的约束进行简要说明：

layouter.constrain_instance(nullifier_hash_cell.cell(), config.clone().instance, 0)?;
layouter.constrain_instance(merkle_root_cell.cell(), config.clone().instance, 1)?;

首先，我们确保nullifier哈希与我们实例列的第一行（我们的公共输入）匹配，然后我们还验证 Merkle 根是否与第二行匹配。

就是这样，就有了我们的 Halo2 Tornado Cash！🥳🥳

接下来要做什么

我之所以多次提到“第二部分文章”，是因为我希望将这第一部分尽可能简单化。以下是我们需要改进电路的内容：

  • 使用真正的哈希函数 → Poseidon
  • 对值进行范围检查

为了更深入地了解 Halo2，我们可以尝试实际生成证明，并生成验证者的 Solidity 合约，这样我们就拥有了一个完全功能的 Tornado Cash。

我还不知道如何做到这一点 😂

拜托！如果你有一些想法或建议，或者如果本文的某些部分需要改进 → 给我发消息。

本翻译由 DeCert.me 协助支持， 在 DeCert 构建可信履历，为自己码一个未来。

点赞 0
收藏 2
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
翻译小组
翻译小组
0x9e64...7c84
大家看到好的文章可以在 GitHub 提 Issue： https://github.com/lbc-team/Pioneer/issues 欢迎关注我的 Twitter： https://twitter.com/UpchainDAO

翻译小组

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！